Leçon 28. Analyse. Fonctions monotones, fonctions convexes

Le¸con 28. Analyse. Fonctions monotones, fonctions convexes.
Applications.
Agr´egation. Universit´e Denis Diderot∗. Paris.
Contents
1 Introduction 1
2 Monotonie. 1
2.1 Monotonieetcontinuit´e................................. 1
2.2 Monotonie et diff´erentiabilit´e. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
3 Convexit´e. 2
3.1 D´efinitions et premi`eres propri´et´es. . . . . . . . . . . . . . . . . . . . . . . . . . . 2
3.2 Convexit´eetint´egration................................. 3
3.3 Crit`eresdeconvexit´e. ................................. 4
3.4 Exemples-Propri´et´es................................... 5
4 Bibliographie. 5
1 Introduction
La convexit´e est un concept important de l’analyse moderne, puisque toute une th´eorie
lui est particuli`erement d´edi´ee : l’analyse convexe. Il s’agit notamment d’asseoir de mani`ere
th´eorique des probl`emes d’optimisation mais aussi de tenter de r´esoudre des probl`emes varia-
tionnels (´equations aux d´eriv´ees partielles). Elle a envahit par son aspect g´eom´etrique beaucoup
de domaines aussi divers que la th´eorie des nombres, la cristallographie, la g´eom´etrie alg´ebrique,
etc.
Les fonctions convexes peuvent ˆetre d´efinies sur des parties d’espaces vectoriels r´eels de
plusieurs dimensions, les fonctions monotones quant `a elles le sont sur des parties de la droite
r´eelle. Ce qui lie ces deux types de fonctions est le fait qu’une fonction convexe suffisamment
r´eguli`ere admet une d´eriv´ee croissante.
C’est pour cela que l’on ´etudiera dans un premier temps les fonctions monotones sur des
parties de R, puis on abordera les fonctions convexes d´efinies sur ces mˆemes parties.
2 Monotonie.
2.1 Monotonie et continuit´e.
Une fonction monotone sur un intervalle de la droite r´eelle a un comportement topologique
agr´eable, ceci est dˆu au fait que la topologie de Rest intimement li´ee `a sa structure ordonn´ee,
le th´eor`eme suivant l’illustre :
∗Auteur et donc responsable de ce contenu : Marzouk Brahim. Pour toute erreur, suggestion ou n’importe
quoi d’autre : [email protected]
1

3 CONVEXIT ´ E. 2
Th´eor`eme 2.1 Une fonction r´eelle d´efinie et monotone sur un intervalle I, de Ra l’ensemble
de ses points de discontinuit´e au plus d´enombrable. De plus elle est born´ee sur tout compact
inclus dans l’int´erieur ˚ I, de I, et admet en tout point de cet int´erieur, une limite finie `a droite
et `a gauche.
On utilise pour la preuve de celui-ci la s´eparabilit´e de la droite r´eelle. On a, ´egalement, en
durcissant un peu le caract`ere monotone :
Th´eor`eme 2.2 Une fonction r´eelle, f, d´efinie, continue et strictement monotone sur un inter-
valle I, r´ealise une bijection de Isur son image par f. En outre la fonction r´eciproque, f−1est
aussi continue et strictement monotone et de mˆeme monotonie que f.
2.2 Monotonie et diff´erentiabilit´e.
Une fonction monotone sur un intervalle admet une propri´et´e plus forte que la continuit´e.
En effet, Lebesgue a prouv´e un th´eor`eme c´el`ebre, dont on peut consulter une preuve dans le
livre de Roger V. JEAN au chapitre ”Diff´erentiation.” :
Th´eor`eme 2.3 (LEBESGUE). Une fonction monotone sur un intervalle est presque partout
d´erivable.
Applications simples de la monotonie.
1. Inversion de fonctions classiques.
2. Comparaison s´erie-int´egrale.
Une application importante de la monotonie est en fait l’obtention de propri´et´es de r´egularit´e
des fonctions convexes.
3 Convexit´e.
Pour cette partie je me suis fortement inspir´e du premier chapitre du livre de Robert
WAYNE et Dale VARBERG.
3.1 D´efinitions et premi`eres propri´et´es.
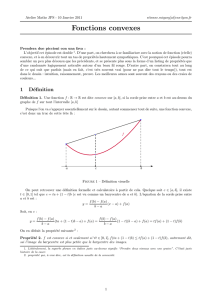
D´efinition 3.1 Soit fune fonction r´eelle d´efinie sur un intervalle I, de la droite r´eelle. On
dit que fest convexe sur Ilorsque pour tous xet yde Iet tout λde [0,1], on a :
f(λx + (1 −λ)y)≤λf(x) + (1 −λ)f(y).(1)
On reprend les notations pr´ec´edentes, on se donne xdans Iet on d´efinit, pour tout
y6=xde I:
δxf(y) = f(x)−f(y)
x−y.
Puis Epi(f) = {(x, y)∈I×R|y≥f(x)}, l’´epigraphe de f. On a alors la caract´erisation suiv-
ante des fonctions convexes, toujours en reprenant les mˆemes hypoth`eses que dans la d´efinition
pr´ec´edente.
Th´eor`eme 3.1 fest convexe sur Isi et seulement si elle v´erifie l’une des deux propri´et´es
´equivalentes suivantes :
•(In´egalit´e des trois pentes). Pour tous x < z < y de I, on a : δxf(z)≤δxf(y)≤δzf(y).

3 CONVEXIT ´ E. 3
•L’´epigraphe de f,Epi(f)est une partie convexe du plan r´eel.
L’in´egalit´e des trois pentes nous donne alors pratiquement toutes les propri´et´es de
r´egularit´e, on a en effet :
Th´eor`eme 3.2 Si fest convexe sur I, alors fadmet en tout point xde ˚ I, une d´eriv´ee `a droite
f0
d(x)et une d´eriv´ee `a gauche f0
g(x)avec f0 g(x)≤f0
d(x). Ces d´eriv´ees sont en plus croissantes
et sont ´egales en dehors d’une partie au plus d´enombrable de I.
On en d´eduit alors que fest continue et mˆeme, grace `a la monotonie des deux d´eriv´ees
qu’elle est continuement diff´erentiable hors d’une partie au plus d´enombrable de I.
3.2 Convexit´e et int´egration.
Th´eor`eme 3.3 Si fest convexe sur un intervalle ouvert Ialors il existe une fonction croissante
gd´efinie sur Iet un r´eel cde Itels que pour tout xde I:
f(x)−f(c) = Zx
c
g(t)dt.
R´eciproquement toute fonction s’´ecrivant sous cette forme int´egrale est convexe.
On peut par la notion d’int´egration d´efinir une dualit´e (de Fenchel-Legendre) agissant sur les
fonctions convexes. Si gest une fonction positive, continue et strictement croissante sur [0,∞[,
s’annulant en 0 et tendant vers l’infini `a l infini. g−1a un sens et a les mˆemes propri´et´es que g.
On d´efinit alors une fonction convexe, f, sur [0,∞[ par :
f(x) = Zx
0
g(t)dt. (x≥0).
Puis sa conjugu´ee pour ydans [0,∞[ par :
f∗(y) = Zy
0
g−1(t)dt. (y≥0).
On a, apr`es ces d´efinitions, l’in´egalit´e d’Young :

3 CONVEXIT ´ E. 4
Th´eor`eme 3.4 Sous les hypoth`eses pr´ec´edentes :
xy ≤f(x) + f∗(y).
Cette in´egalit´e permet d’obtenir celle de Minkowski-Hold¨er qui suit.
Application : in´egalit´e de Hold¨er-Minkowski. Soit pet qdeux r´eels strictement positifs tels
que 1/p + 1/q = 1. Alors pour tous r´eels positifs uet v,ona:
uv ≤up
p+vq q.
Une importante application de la convexit´e est l’in´egalit´e de JENSEN, qui donne entre-
autres, les in´egalit´es des moyennes.
Th´eor`eme 3.5 Soit µune mesure de probabilit´e sur un espace mesur´e, Ω. Soit fune fonction
r´eelle sur Ω,µ-int´egrable et `a valeurs dans un intervalle ouvert I. Si φest une fonction r´eelle
et convexe sur I, alors on a :
φ(ZΩ fdµ)≤ZΩ (φ◦f)dµ.
Application : In´egalit´e des moyennes.
Soit α1, , . . . , αn,nr´eels strictement positifs tels que Pi=n
i=1 αi= 1 alors pour tous r´eels
positifs y1, . . . yn, on a :
yα1
1yα2 2. . . yαn
n≤
i=n
X
i=1
αiyi.
3.3 Crit`eres de convexit´e.
Si fest suffisament r´eguli`ere sur ˚ Ion a des crit`eres sur ses d´eriv´ees successives :
Th´eor`eme 3.6 Si fest d´erivable sur un ouvert de la droite r´eelle, elle y est convexe si et
seulement si sa d´eriv´ee est croissante. Si en outre elle est deux fois d´erivable cette condition est
´equivalente `a la positivit´e de sa d´eriv´ee seconde.
Ce th´eor`eme se g´en´eralise `a plusieurs dimensions.
Th´eor`eme 3.7 Soit Uun ouvert convexe d’un espace vectoriel r´eel de dimension finie et fune
fonction r´eelle d´efinie et deux fois diff´erentiable sur U. Alors fest convexe sur Usi et seulement
si d2fest d´efinie et positive sur tout U.

4 BIBLIOGRAPHIE. 5
3.4 Exemples-Propri´et´es.
Les fonctions convexes sont stables par passage `a la borne sup´erieure, par addition et
multiplication positive. La fonction exponentielle sur la droite r´eelle est convexe ainsi que la
fonction xlog(x) sur R+.
4 Bibliographie.
•Jean-Jacques PRAT, Jacques VAUTHIER. Cours d’analyse de l’Agr´egation. Masson.
•Roger V. JEAN. Mesure et int´egration. Presses de l’Universit´e du Qu´ebec.
•Nicolas BOURBAKI. Fonctions d’une variable r´eelle. Hermann.
•A.Wayne ROBERTS, Dale E. VARBERG. Convex Functions. Academic Press.
•Walter RUDIN. Real and complex analysis. Mac Graw-Hill.
Universit´e Denis DIDEROT.
Marzouk Brahim.
[email protected]