BTS Et 2006 Metro Cor

Durée : 4 h
Physique Appliquée Pré-étude et modélisation
Coefficient : 3
BTS 2006
Motorisation d'un tramway
Métropole
Calculatrice autorisée
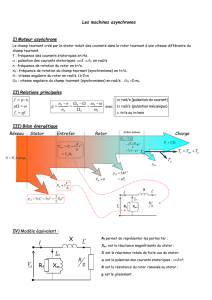
MAS Meca Harmonique Transitoire Onduleur
Correction
- Partie A - Étude d'un moteur de traction
A.1. Etude du fonctionnement nominal du moteur
A.1.1. de
/tr s
f p n
on tire
60
S
Nn
fp
avec les notations du problème
88
60 60 2
2640
n
S
f
pn
Le nombre de paire de pôle est de 2.
A.1.2. Par définition
2640 2610 0,01136
2640
S
S
NN
gN
Le glissement est donc g=1,14%
A.1.3.
3 cos 3 585 35,4 0,732 26,25
n N N N
P U I kW
Comme les pertes dans le fer et les pertes joules stator sont négligeables on aura
PtrN
Pjr = gPtr
Pu
Pjs = 0
Pfs = 0
PN
26,3
N trn
P P kW
A.1.4. A partir de
2
60
trn n S n S
P C C n
donc
3
26,3 10 95,13
22
2640
60 60
tr N
n
S
P
C Nm
N
Le couple nominal est donc
95,13
n
C Nm
A.1.5. On sait que les pertes joules stator valent
3
0,01136 26,3 10 298
jrN n trN
p g P W    
Les pertes joules rotoriques sont donc de
298
jrN
pW
A.1.6. Les pertes mécaniques étant négligées , la puissance utile développée par le moteur est donnée
par
26300 298 26,0
uN tr N jr N
P P p kW    
.
La puissance utile développée par le moteur est donc
26,0
uN
P kW
A.2. Expression simplifiée du moment du couple électromagnétique
A.2.1. D’après le schéma on a
03
338 23,0
26,6 10 2 88
M
V
IA
L
.
Le courant magnétisant est donc
023,0IA
A.2.2. D’après le modèle on a
22
rV
IR
g

A.2.3. Quand le glissement diminue on peut s’attendre à ce que
R
g
devienne de plus en plus grand
devant . En effet
3
0,147 14,7 2,38 10 2 88 1,31
0,01
R
g
Alors
2
rVg
IV
R
R
g
donc
rg
IV
R
A.2.4. On a
2
3
tr r
R
PI
g
donc
2
22
3
tr RV
Pg
gR
A.2.5.En remplaçant
rg
IV
R
dans
2
3
tr r
R
PI
g
, on obtient
3
tr R
Pg2 g2
2
V
R
Soit
2
3
tr V
Pg
R
et comme
tr S
PC 
donc
2
3
tr
SS
PV
Cg
R
de la forme
C k g
avec
2
3 8433
S
V
k Nm
R
A.3. Fonctionnement en traction
A.3.1. Avec
8433Cg
et C=170 Nm alors
2
170 2,02 10
8433
C
gk
soit
2
2,02 10 2%g
A.3.2. Alors
1 2640 (1 0,0202)
S
N N g    
donc
2587 tr/minN
A.3.3. De
0,0202
338 0,147
rg
IV
R
donc
46,4
r
IA
A.3.4. On voit que
3
0,0202 2,38 10 2 88
tan 0,180
0,147
rg
RR
g
soit
arctan0,180 10,2
r
A.3.5. Construction de Fresnel
0
I
est de 23 A et en retard de 90° sur
V
r
I
est de 46,4 et en retard de 10,2° sur
V
avec l’échelle 5A/cm on a
V
R
I
0
I
10,2
A.3.6. De
0r
i i i
donc
0r
I I I
d’où la construction ci dessous

V
R
I
55IA
0
I
34
0
I
A.3.7 On mesure sur la construction
55IA
et
34,5
A.3.8. Avec
3 cos 3 338 55 cos34,5 45961P VI
on trouve donc P=46000 W ( bien loin de
Pun)
Partie B – Performances mécaniques du tramway
B.1) Expression de la vitesse de rotation du rotor en fonction de la vitesse de déplacement du
tramway
De
2
3,6 2 3,6
roue roue
Dv
vD
et
10
roue
donc
2
10 10 3,6
roue vD
Donc
20
3,6 0,52 v 
10,7 v   
B.2) Performances maximales de la rame de tramway
B.2.1) Fonctionnement en régime permanent sur le plat
B.2.1.1) Pour M = 60 tonnes
43
1
16,2
2,7 10 60 10 0,135
R
Cv
Pour v=0 :
116,2 R
C
Nm
Pour v=60km/h
116,2 0,135 60 24,3 R
C   
Nm
B.2.1.2) La vitesse v1 vaut alors 60 km/h
B.2.1.3)
116,2 0,135 60 24,3 R
C Nm   
110,7 10,7 60 642 /v rad s     
ou
1
1642
60 60 6130tr/ min
22
n
1 1 1 24,3 642 15600 R
P C W    
Rq : 642>>276 rad/s du régime nominal du moteur !
CR1
16
24,3
CR2
144
152
B.2.2) Régime permanent sur une pente de 8%
B.2.2.1) Pour M=60 tonnes
33
2
144
2,4 10 60 10 0,135
R
Cv
Pour v=0 :
2144 R
C
Nm
Pour v=60km/h
2144 0,135 60 152.1 R
C   
Nm

B.2.2.2) La vitesse v2 vaut alors 28 km/h
B.2.1.3)
2144 0,135 28 147,8 R
C Nm   
110,7 10,7 28 299,6 /v rad s     
ou
1
1299,6
60 60 2861tr/ min
22
n
1 1 1 147,8 299,6 44280 R
P C W    
B.2.3) Démarrage sur le plat
B.2.3.1) La relation fondamentale de la dynamique est
R
d
J C C
dt
B.2.3.2) Lors du démarrage
170 16,2 35 rad ²
4,4
R
CC
ds
dt J
B.2.3.3) Pour atteindre 25 km/h soit 267 rad/s avec une accélération de 35 rad/s², comme
267,5 0
35 rad ²
ds
dt t
alors il faudra
267,5 7,6
35
ts
- Partie C – Etude de l’onduleur
C.1. Onduleur à commande pleine onde
C.1.1. Lorsque K1 est fermé
02C AU
V
, K4 fermé
02C AU
V
d’où la courbe VAO
C.1.2. tracé de VBO et VCO
C.1.3. Tracé de VAN
C.1.4.
22
2
22
3 6 3 6 3
2
CC
C
AN
UU
TT
U
VT
C.1.5. Le fondamentale de van est
12
( ) sin
C
U
v t t
et sa valeur efficace est
1222 750 338
2
CC
UU
VV
C.2. Association onduleur –moteur
C.2.1.
3
5
3
7
5 2,31 10 5 553 6,39
7 2,31 10 7 553 8,94
ZL
ZL
C.2.2.
1
5
555
7
77
510,6
5,4
V
V
IA
ZZ
V
IA
Z
C.2.3. On en déduit
11 5 7
33
( ) cos sin 6
SS
EI E
C t I I t

Donc
11
33 309 35,4
cos cos 43 6,2 95
5532
S
p
EI
C Nm
et
57
3
( ) sin 6
S
E
C t I I t
La fréquence de C’(t) est 6x88=528 Hz
Et l’amplitude de C’(t) est
57
317,4
MAX S
E
C I I Nm  
Donc
( ) 95 17,4sin 6 2 88C t t
C.2.4. le rapport
17,4 0,18
95
MAX
CC
Le couple pulsatoire représente environ 20% du couple nominal, d’où une nuisance sonore, usure
prématurée, vibrations.
C.2.5. L’harmonique le plus proche est du rang 17, il sera plus facile de l’éliminer par des filtres (
bobines)