thermochimie

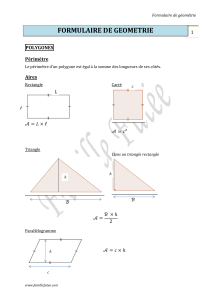
Thermodynamiquechimique
1. L’enthalpiestandardderéaction
Ondéfinitpourchaqueréactionàunetempératuredonnée,lachaleurderéactionéchangéeà
pressionconstante.Lapressionstandardestaujourd’huilapressionde1bar=105Pa.La
températurestandardestlatempératurede25°Csoit298K.
Exemples:
N2+3H2→2NH3avec∆
=‐92,4kJ.mol‐1
2Fe+3/2O2→2Fe2O3avec∆
=‐823,5kJ.mol‐1
Al’aidedesvaleursdonnéesdansleslivresderéférence,lehandbookparexemple,onpeut
calculerl’enthalpielibreàtoutetempérature:∆
∆  ∑
2. LaloideHess
Lorsd’uneréactionchimique,onpeutcalculerl’enthalpiederéactionàpartirdesenthalpies
deformationdesréactifsetdecellesdesproduitsd’où:
∆é
∆
∆é
Onnoteraquel’enthalpiedeformationd’uncorpspursimpleestprisecommeunétatde
référenceégalà0.
‐ Exemple:
C3H8+5O2→3CO2+4H2O
Lesenthalpiesdeformationsont:
C+O2→CO2avec∆
=‐393kJ.mol‐1
H2+½O2→H2Oavec∆
=‐286kJ.mol‐1
3C+4H2→C3H8avec∆
=‐104kJ.mol‐1
d’où∆é
=3x(‐393)+4(‐286)–(‐104)=‐2219kJ.mol‐1
‐ Applicationàladéterminationdelatempératuredeflammeadiabatique:
Laréactiondansl’air(79%N2pour21%O2envolume)est:
C3H8+5(O2+3,76N2)→3CO2+4H2O+18,8N2
Lachaleurderéactionpermetdechaufferlesproduits.Ondonne:
pourl'eau:LV=40,5kJ.mol‐1etlesvaleursdeschaleursmolaires
C
p
enJ.mol‐1.K‐1
eauliquide 75,5
vapeurd'eau 34
CO237
N227
D’où:2219000=(3x37+18,8x27)(T‐25)+4(75,5x75+40500+34(T‐100)).
OnendéduitunetempératureT=2734°C.
Latempératureréelleestinférieurecarilyaunexcèsd’airparrapportauxconditions
stœchiométriques.

3. Laloid’actiondemasse
ConsidéronslaréactionaA+bB⇔cC+dDréaliséeàpetTdonnés
OnadoncdG=Vdp–SdT+∑μdn=∑μdn=0
Ainsi,μAda+μBdb+μCdc+μDdd=0
Endéfinissantl’avancementdelaréactiondξ=
=
D’où:‐aμA‐bμB+cμC+dμD=0.Enremplaçantchacundestermesparμ=μ0+RTLnp,onen
déduitlaloid’actiondemasse:ΔG0=‐RTLnKpavecKp=
4. Conséquencesdelaloid’actiondemasse
OnpeutcalculerΔG0parlarelationΔG0=ΔH0‐TΔS0.ΔH0etΔS0sontdéterminésparlestables.
Ainsionpeutcalculerlaconstanted’équilibreKp=ΔG
a. Influencedelatempérature
SiKp≥1,laréactionestdéplacéeversladroite.SiKp≤1,laréactionestdéplacéeversladroite.
Onadoncunetempératured’inversiondel’équilibredelaréactionquandKp=1etdoncpour
Ti=
Δ
Δ .
OnpeutécrireΔG0=ΔH0‐TΔS0=‐RTLnKpsouslaformeLnKp=‐(ΔH0‐TΔS0)/RTeten
dérivantonobtientlaloideVan’tHoff:
 =
Δ
SiΔH0≥0,laréactionestendothermiqueetquandTaugmente,laréactionestdéplacéeversla
droite.
SiΔH0≤0,laréactionestexothermiqueetquandTaugmente,laréactionestdéplacéeversla
gauche.
C’estuneloidemodération.Laréactionréagitenmodérantl’interventiondumilieuextérieur.
Silaréactionestexothermiqueetquelatempératureaugmente,laréactionréagitenessayant
deréduirel’augmentationdelatempérature.C’estdonclaréactionendothermiquequiest
favoriséeetparconséquentlaréactionestdéplacéeverslagauche.Etréciproquement!
b. Influencedelapression
Conséquencedecetteloidemodération,quandlapressionaugmentelaréactionréagitdans
lesensquidiminuelenombredemolesdegaz.
Exemple:
N2+3H2⇔2NH3lasynthèsedel’ammoniacestfavoriséeparl’augmentationdelapression.
5. Lediagrammed’Ellingham
Considéronsuneréactiond’oxydationd’unmétal2M+O2→2MOavecΔG0=ΔH0‐TΔS0.On
peuttracerΔG0=f(T)quiestunedroite.
Exemple:2Mn+O2→2MnO
Mn O2MnO
H0fenkJ.mol‐100‐384
S0fenJ.mol‐1.K‐132205 60

AinsiΔG0=‐768000+149T:
0 500 1000 1500 2000
800
700
600
500
400
T en °C
enthaplpie libre en kJ.mol-1
Considérons2métaux.2M1+O2→2M1OavecΔG01et2M2+O2→2M2OavecΔG02.
LesensdelaréactionestimposéparlesvaleursrespectivesdeΔG02etdeΔG01.M2réduitM1si
ΔG02<ΔG01:
Souventles2droitessecoupent:
Ainsi,ilexisteunetempératured’inversionoùlesensdelaréactions’inverse.Au‐dessus,c’est
M1quidevientleplusréducteur.
L’ensembledescourbesseretrouventdanslediagrammed’Ellinghampourlesoxydes.
ΔG0
T
Ti
2M1+O2→2M1O
2M2+O2→2M2O
ΔG0
T
2M1+O2→2M1O
2M2+O2→2M2O