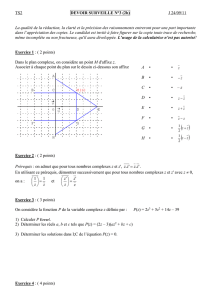
1

2
1
/
2
100%