rappel du cours - Artemath... des maths et autres choses

Athénée Royal d’Uccle 1
Cours de
Mathématique
6ème année
Cours à 6 périodes
hebdomadaires
Les bases
A.Droesbeke
Version : 2014
2
Table des matières
Préface
1
I
1
Algèbre
1 Calcul matriciel
1.1
Définition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
1.2
Opérations sur les matrices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
1.2.1
Transposée d’une matrice . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
1.2.2
Égalité de deux matrices . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
1.2.3
Addition de deux matrices . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
1.2.4
Multiplication d’une matrice par un réel . . . . . . . . . . . . . . . . . . .
5
1.2.5
Multiplication de deux matrices . . . . . . . . . . . . . . . . . . . . . . . .
5
1.2.6
Inversion de matrice . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
1.3
II
3
Analyse
9
2 Les limites
11
2.1
Limites d’une suite . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
11
2.2
Les nombres réels . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
12
2.2.1
Définition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
12
2.2.2
La droite réelle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
12
Limites d’une variable . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
15
2.3.1
Limites finies . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
15
2.3.2
Limite infinie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
15
Limites d’une fonction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
16
2.4.1
Limite finie d’une fonction lorsque x tend vers une valeur finie . . . . . . .
16
2.4.2
Limites infinie lorsque x tend vers une valeur finie . . . . . . . . . . . . . .
18
2.4.3
Limite finie lorsque x tend vers une valeur infinie . . . . . . . . . . . . . .
19
2.4.4
Limite infinie lorsque x tend vers une valeur infinie . . . . . . . . . . . . .
21
Opérations sur les limites . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
23
2.3
2.4
2.5
i
ii
TABLE DES MATIÈRES
2.6
2.7
Cas d’indétermination
0
2.6.1 Cas
. . . . .
0
∞
2.6.2 Cas
. . . . .
∞
2.6.3 Cas ∞ − ∞ . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
24
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
25
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
26
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
27
Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
28
3 Les asymptotes
31
3.1
Définition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
31
3.2
Point adhérent au domaine . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
32
3.3
Asymptotes verticales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
32
3.3.1
Premier exemple . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
33
3.3.2
Deuxième exemple . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
33
3.3.3
Troisème exemple . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
34
3.3.4
Remarque importante . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
34
Asymptotes horizontales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
35
3.4.1
Premier exemple . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
35
3.4.2
Deuxième exemple . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
36
3.4.3
Troisième exemple . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
37
3.4.4
Remarque importante . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
37
Asymptotes obliques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
38
3.5.1
Remarque concernant le calcul des asymptotes horizontales et obliques . .
39
3.5.2
Premier exemple . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
39
3.5.3
Deuxième exemple . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
41
3.5.4
Remarque importante . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
41
3.6
Position d’une courbe par rapport à une asymptote . . . . . . . . . . . . . . . . .
42
3.7
Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
45
3.8
Solutions des exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
46
3.4
3.5
4 Les dérivées
4.1
4.2
47
Rappels . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
47
4.1.1
Accroissements et taux d’accroissement . . . . . . . . . . . . . . . . . . . .
47
4.1.2
Coefficient angulaire d’une droite . . . . . . . . . . . . . . . . . . . . . . .
48
4.1.3
Sécante à une courbe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
48
4.1.4
Tangente à une courbe . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
49
Nombre dérivé et fonction dérivée . . . . . . . . . . . . . . . . . . . . . . . . . . .
49
4.2.1
Exemple introductif . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
49
4.2.2
Définitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
51
4.2.3
Autre formulation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
51
4.2.4
Propriétés . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
51
4.2.5
Dérivabilité et continuité . . . . . . . . . . . . . . . . . . . . . . . . . . . .
52
iii
TABLE DES MATIÈRES
4.3
Equation d’une tangente à une courbe . . . . . . . . . . . . . . . . . . . . . . . .
53
4.4
Formules de dérivation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
53
4.4.1
Dérivée d’une constante . . . . . . . . . . . . . . . . . . . . . . . . . . . .
53
4.4.2
Fonction identité . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
53
4.4.3
Puissances entières de x . . . . . . . . . . . . . . . . . . . . . . . . . . . .
54
4.4.4
Racine carrée de x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
54
4.4.5
Puissance quelconque de x . . . . . . . . . . . . . . . . . . . . . . . . . . .
55
Opérations sur les dérivées . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
55
4.5.1
Dérivée d’une somme de fonctions . . . . . . . . . . . . . . . . . . . . . . .
55
4.5.2
Dérivée d’un produit de fonctions . . . . . . . . . . . . . . . . . . . . . . .
56
4.5.3
Dérivée d’un produit d’une fonction par une constante . . . . . . . . . . .
56
4.5.4
Dérivée d’un quotient de fonctions . . . . . . . . . . . . . . . . . . . . . . .
57
4.5.5
Cas particuliers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
57
Dérivée de la composée de deux fonctions . . . . . . . . . . . . . . . . . . . . . . .
58
4.6.1
Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
58
4.6.2
Formule de dérivation
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
58
4.7
Dérivées successives . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
59
4.8
En résumé . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
59
4.9
Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
60
4.10 Solutions des exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
61
4.5
4.6
5 Applications de la dérivée
5.1
63
Croissance et décroissance . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
63
5.1.1
Rappels : croissance, décroissance, minimum et maximum . . . . . . . . . .
63
5.1.2
Lien entre dérivée première et croissance . . . . . . . . . . . . . . . . . . .
64
5.1.3
Extremums . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
64
Dérivée seconde et concavité . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
65
5.2.1
Approche intuitive . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
65
5.2.2
Concavité et dérivée seconde . . . . . . . . . . . . . . . . . . . . . . . . . .
65
5.2.3
Point d’inflexion
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
66
Cas particuliers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
66
5.3.1
Point anguleux . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
66
5.3.2
Point de rebroussement . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
66
Etudes de fonctions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
67
5.4.1
Plan de travail . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
67
5.4.2
Premier exemple . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
68
5.4.3
Deuxième exemple . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
71
5.5
Problème d’extrémum . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
74
5.6
Théorème des valeurs intermédiaires . . . . . . . . . . . . . . . . . . . . . . . . . .
75
5.7
Résolution numérique d’équations . . . . . . . . . . . . . . . . . . . . . . . . . . .
75
5.2
5.3
5.4
iv
TABLE DES MATIÈRES
5.8
III
5.7.1
Méthode de dichotomie . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
76
5.7.2
Méthode de Newton . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
77
Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
79
Géométrie
6 Calcul vectoriel dans l’espace
85
87
6.1
Définitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
87
6.2
Opérations sur les vecteurs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
88
6.2.1
Vecteurs égaux . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
88
6.2.2
Vecteurs opposés . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
88
6.2.3
Somme de vecteurs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
89
6.2.4
Différence de deux vecteurs . . . . . . . . . . . . . . . . . . . . . . . . . .
91
6.2.5
Produit d’un vecteur par un réel . . . . . . . . . . . . . . . . . . . . . . . .
92
6.2.6
Propriétés des opérations sur les vecteurs . . . . . . . . . . . . . . . . . . .
92
Vecteurs particuliers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
93
6.3.1
Vecteurs parallèles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
93
6.3.2
Points colinéaires . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
93
6.3.3
Combinaison linéaire de vecteurs . . . . . . . . . . . . . . . . . . . . . . .
94
6.3.4
Points coplanaires . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
94
6.4
Base du plan . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
94
6.5
Expression d’un vecteur dans un repère orthonormé . . . . . . . . . . . . . . . . .
94
6.6
Opérations sur les vecteurs et composantes . . . . . . . . . . . . . . . . . . . . . .
95
6.6.1
Egalité de vecteurs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
95
6.6.2
Somme de vecteurs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
95
6.6.3
Produit d’un vecteur par un réel . . . . . . . . . . . . . . . . . . . . . . . .
96
6.6.4
Vecteurs opposés . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
96
6.6.5
Composantes d’un vecteur quelconque . . . . . . . . . . . . . . . . . . . .
96
Produit scalaire . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
98
6.7.1
Définition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
98
6.7.2
Cas particuliers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
98
6.7.3
Produit scalaire de deux vecteurs perpendiculaires . . . . . . . . . . . . . .
99
6.7.4
Produit scalaire dans un repère orthonormé . . . . . . . . . . . . . . . . .
99
6.7.5
Applications . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
99
6.3
6.7
6.8
Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101
v
TABLE DES MATIÈRES
IV
Trigonométrie
103
7 Rappel de trigonométrie
105
7.1
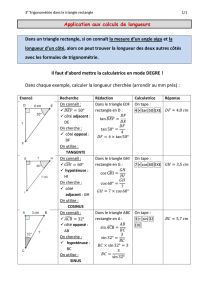
Nombres trigonométriques d’un angle dans un triangle rectangle . . . . . . . . . . 105
7.2
Le cercle trigonométrique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 106
7.3
Identités fondamentales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 108
7.4
Angles remarquables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109
7.5
Angles associés . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109
7.6
Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110
8 Formules de transformation
8.1
8.2
113
Formules d’addition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113
8.1.1
Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113
8.1.2
Formules des cosinus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113
8.1.3
Formules des sinus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115
8.1.4
Formules des tangentes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115
Formules de duplication . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115
8.2.1
Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115
8.2.2
Formules du cosinus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 116
8.2.3
Formule des sinus et des tangentes . . . . . . . . . . . . . . . . . . . . . . 116
8.3
Formules de Carnot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 116
8.4
Formules de Simpson . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 116
8.5
Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 118
9 Equations et inéquations trigonométriques
121
9.1
Définition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 121
9.2
Equations trigonométriques élémentaires . . . . . . . . . . . . . . . . . . . . . . . 121
9.3
9.2.1
Equation élémentaire du type sin x = sin a . . . . . . . . . . . . . . . . . . 121
9.2.2
Equation élémentaire du type cos x = cos a . . . . . . . . . . . . . . . . . . 122
9.2.3
Equation élémentaire du type tan x = tan a . . . . . . . . . . . . . . . . . . 122
Equations trigonométriques quelconques . . . . . . . . . . . . . . . . . . . . . . . 123
9.3.1
9.4
Classification des équations trigonométriques . . . . . . . . . . . . . . . . . 123
Inéquations trigonométriques
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 128
9.4.1
Remarque préliminaire . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 129
9.4.2
Inéquations trigonométriques simples . . . . . . . . . . . . . . . . . . . . . 129
9.4.3
Inéquations trigonométriques complexes . . . . . . . . . . . . . . . . . . . 132
9.5
Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 135
9.6
Solutions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 136
vi
TABLE DES MATIÈRES
V
Annexes
137
Formulaires . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 139
.1
Formulaire de trigonométrie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 139
.2
Fomrulaire de dérivées . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 142
Liste des illustrations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 142
Préface
Ce cours de base de 6ème année (cours à 6 périodes hebdomadaires) est une première ébauche
de ce que sera le cours futur. Il comporte encore énormément de "coquilles". Si vous en trouvez,
n’hésitez pas à m’en faire part, le cours ne pourra que s’en améliorer... (les corrections peuvent
être suggérées à partir du site www.artemath.com)
Merci d’avance et bonne lecture...
Cette création est mise à disposition selon le Contrat Paternité-Pas d’Utilisation CommercialePartage des Conditions Initiales à l’Identique 2.0 France.
Ce document est disponible en ligne (http ://creativecommons.org/licenses/by-nc-sa/2.0/fr/) ou
par courrier postal à Creative Commons, 171 Second Street, Suite 300, San Francisco, California
94105, USA.
1
2
PRÉFACE
Première partie
Algèbre
1
Chapitre 1
Calcul matriciel
1.1
Définition
Définition: Une matrice est un tableau rectangulaire de nombres.
D’une manière générale, on écrira :


a11 a12 · · · a1p
 a21 a22 · · · a2p 


An×p =  ..
..
.. 
 .
. ··· . 
an1 an2 · · · anp
Les lignes et les colonnes sont les rangées de la matrice.
Les nombres aij s’appellent les éléments de la matrice.
aij est l’élément de la matrice situé à l’intersection de la
ième ligne et à la j ème colonne.
Le nombre n de lignes et le nombre p de colonnes sont les
dimensions (ou le format) de la matrice.
• Lorsque n = 1, on parle de matrice ligne
• Lorsque p = 1, on parle de matrice colonne
• Lorsque n = p, on parle de matrice carrée
Exemple Considérons la matrice
3 4 8
2 5 −9
Les nombres 3, 4 et 8 forment la première ligne (L1 ) ; les nombres 2, 5 et -9 forment
la deuxième ligne (L2 ). De même, 3 et 2 forment la première colonne (C1 ),...
Définition: La matrice unité de dimension n est une matrice carrée ne contenant que des 1 et uniquement sur la diagonale.


1 0 0 ··· 0
 0 1 0 ··· 0 




In =  0 0 1 · · · 0 
 .. ..
. . 
 . . · · · .. .. 
0 0 0 ··· 1
3
4
CHAPITRE 1. CALCUL MATRICIEL
1.2
Opérations sur les matrices
1.2.1
Transposée d’une matrice
Définition: La matrice transposée de la matrice A, notée t A (ou At ) est
la matrice obtenue en permutant les lignes et les colonnes
de A. Si


a11 a12 · · · a1p
 a21 a22 · · · a2p 


An×p =  ..
..
.. 
 .
. ··· . 
an1 an2 · · · anp
alors

t


An×p = 

Exemple
A=
et
a11 a21
a12 a22
..
..
.
.
a1p a2p
· · · an1
· · · an2
.
· · · ..
3 4 8
2 5 −9
· · · anp







3 2
t
A= 4 5 
8 −9
Remarquons que l’on a :
t
1.2.2
t
A =A
Égalité de deux matrices
Définition: Deux matrices de même format sont égales si et seulement
si les éléments correspondants sont égaux.
An×p = Bn×p ⇔ ∀i ∈ {1...n} , ∀j ∈ {1...p} : aij = bij
1.2.3
Addition de deux matrices
Pour pouvoir additionner deux matrices, il faut qu’elles aient le même format.
Définition:
An×p = Bn×p + Cn×p ⇔ ∀i ∈ {1...n} , ∀j ∈ {1...p} : aij = bij + cij
5
1.2. OPÉRATIONS SUR LES MATRICES
Exemple SoientA = A =
1.2.4
3 4 8
2 5 −9
1
et B =
2
4
A+B =
4
2 −5
0 3
6 3
5 −6
Multiplication d’une matrice par un réel
On considère une matrice An×p et un réel k, on a :
Définition:
Bn×p = k.An×p ⇔ ∀i ∈ {1...n} , ∀j ∈ {1...p} : bij = k.aij
1.2.5
Multiplication de deux matrices
Pour multiplier deux matrices, il faut que le nombre de colonnes de la première matrice soit égal au nombre de lignes de la seconde.
Définition: On obtient l’élément cij de la matrice produit en effectuant
la somme des produits des éléments de la ième ligne de la
première matrice avec les éléments correspondants de la
jème colonne de la seconde matrice.
Cn×m = An×p ×Bp×m ⇔ ∀i ∈ {1...n} , ∀j ∈ {1...m} : cij = ai1 .b1j +ai2 .b2j +...+aip .bpj =
Remarques • Il se peut que le produit A × B a existe mais que le produit B × A existe
• Le produit matriciel n’est pas commutatif
a. On omettra souvent le symbole × pour le remplacer par un point ou, le plus souvent, par
rien du tout !
1.2.6
Inversion de matrice
Il n’est pas possible en pratique de diviser deux matrices. On parle alors d’inversion de
matrice.
En effet, par analogie aux nombres réels, deux nombres sont inverse l’un de l’autre si leur produit
vaut 1.
On a
1
.x = 1
x
ou
x−1 .x = 1
Définition: La matrice A−1 sera l’inverse de la matrice A si
A−1 A = AA−1 = I
6
CHAPITRE 1. CALCUL MATRICIEL
Il ressort de cette définition que l’on ne peut inverser que des matrices carrées.
L’inversion de matrice sera vue essentiellement dans le chapitre sur les déterminants 1 .
1. Voir cours de rhétos
7
1.3. EXERCICES
1.3
Exercices
Remarque préliminaire : On pensera régulièrement à vérifier les
résultats avec la calculatrice ! ! !
1. Calculer A + B et 2A − 3B dans les
5 −2
4
(a) A =
et B =
1 3
−3
0 −2 7
(b) A =
et B =
5 4 −3
cas suivants :
1
2
8 4 0
0 1 4
2. Calculer, si possible, les produits A.B et B.A si




3 0 −1
1 −5 0
2  et B =  4 1 −2 
(a) A =  0 4
5 −3 1
0 −1 3

4 −2 0

2 1 0 −3
1
1 −2
(b) A =
et B = 
 0
−7 0 −2 4
0
5
−3 −1 0
1 2
2 −1
3
3. Soient A =
,B=
et C =
0 −3
3 1
−2
Vérifier si




1
0
.
(a) (A + B)(A − B) = A2 − B 2
(b) A(B + C) = AB + AC




1 2 3
0 1 2
4. Soient les matrices A =  −1 2 −3  et B =  3 −2 1 .
2 1 2
1 2 1
Calculer A + B ; B + A ; A.B ; B.A.


 
 
1 2
3
0
1
5. Soit les matrices A =  2 2 −3 , x =  3 et y =  2 
3 −3 2
1
3
t
t
t
Calculer la transposée de A( A), Ax, yAx et xAy. Conclure.


1 −1 −1
6. Soit la matrice A =  −1 1 −1 .
−1 −1 1
(a) Calculer A2
(b) Montrer que A2 = A + 2I 2
(c) Déterminer une matrice B tel que AB = I
−15 3 − 3a
−12 0
7. Soient les matrices A =
et B =
0
2
0 5
Pour quelle(s) valur(s) de a a-t-on (A + B)2 = A2 + 2AB + B 2
2. I est la matrice unité
8
CHAPITRE 1. CALCUL MATRICIEL


1 1 0
8. On considère la matrice A =  0 1 1 
0 0 1
(a) Calculer A2 , A3 et A4


1 an b n
(b) Montrer que pour tout entier n ∈ N, An peut s’écrire sous la forme An =  0 1 an 
0 0 1
(c) Déterminer les valeurs de an et bn en fonction de n
Deuxième partie
Analyse
9
Chapitre 2
Les limites
2.1
Limites d’une suite
Définition: La suite an converge vers le réel a si la différence an − a
devient quasi nulle lorsque n augmente sans cesse (prend
toutes les valeurs successives de N0 ).
On notera alors :
lim an = a
n→∞
Exemples Les suites des exemples ?? et ??
Définition: La suite an tend vers l’infini si an croît sans borne lorsque
n augmente sans cesse.
On notera alors :
lim an = +∞
n→∞
Exemples Les suites des exemples ?? et ??
Définition: La suite an tend vers moins l’infini si an décroît sans borne
lorsque n augmente sans cesse.
On notera alors :
lim an = −∞
n→∞
La suite n’a pas de limite si aucune des trois situations ci-dessus ne se présentent.
11
12
CHAPITRE 2. LES LIMITES
2.2
2.2.1
Les nombres réels
Définition
Les années passées, nous avons étudié :
• l’ensemble des naturels N = {0, 1, 2, ...} ;
• l’ensemble des nombres entiers Z = {..., −3, −2, −1, 0, 1, 2, 3, ...} ;
• l’ensemble des nombres rationnels Q c’est-à-dire l’ensemble des nombres pouvant s’écrire
sous
la forme du quotient
o de deux nombres entiers (le second n’étant pas nul) : Q =
n
a
x|x = , a ∈ Z, b ∈ Z0 .
b
Un nombre rationnel peut s’écrire sous la forme d’un nombre décimal limité ou illimité
périodique.
• l’ensemble des nombres irrationnels I c’est-à-dire les nombres décimaux illimités non périodiques. Un tel nombre ne peut jamais s’écrire sous la forme d’une fraction à termes
entiers
L’ensemble R des nombres réels est la réunion des ensembles des nombres rationnels et irrationnels.
On a :
Q
R
I
Z
N
2.2.2
La droite réelle
Définition
Définition: La droite réelle est une droite sur laquelle on a choisi :
• un point O, appelé origine, d’abscisse 0 ;
• un sens positif que l’on indique par une flèche ;
• une unité de mesure.
13
2.2. LES NOMBRES RÉELS
D’habitude, mais rien n’oblige à se conformer à cette habitude, la droite réelle est dessinée
horizontalement, le sens positif choisi de gauche à droite et l’unité en fixant un deuxième point
sur la droite. Son abscisse sera le nombre 1.
M
O
N
x
R
y
Si le nombre y est positif, nous le représenterons par un point N situé sur la droite graduée
à une distance y à droite du point O. De même, si x est négatif, nous le représenterons par un
point M situé sur la droite graduée à une distance −x à gauche du point O.
Cette construction crée une correspondance biunivoque entre les nombres réels et les points de la
droite : à chaque nombre réel correspond un et un seul point de la droite graduée et réciproquement
à chaque point de la droite graduée correspond un et un seul nombre réel (appelé l’abscisse du
point).
Valeurs approchées - Encadrements
Définition: Les valeurs approchées par défaut a et par excès b − α du
réel r à l’approximation α près sont des réels tels que :
a<r<b
L’approximation sur un réel r est la différence entre la valeur approchée par excès et la valeur approchée par défaut.
α=b−a
L’intervalle [a, b] est l’encadrement du réel r.
Exemple Valeurs approchée de π=3.141592...
par défaut
3
3.1
3.14
par excès
4
3.2
3.15
approximation
1
0.1
0.01
encadrement
π ∈ [3; 4]
π ∈ [3.1; 3.2]
π ∈ [3.14; 3.15]
3<π<4
3.1<π<3.2
3.14<π<3.15
Propriétés
Propriété 1 Entre deux nombres réels quelconques, il existe toujours des nombres rationnels
et des nombres irrationnels.
Géométriquement, cela signifie qu’entre deux points quelconques de la droite
graduée, on peut toujours trouver des points d’abscisse rationnelle et des points
d’abscisse irrationnelle. Exemples :
3.5 < 3.55 < 3.6
3.5 < 3.5532584... < 3.6
14
CHAPITRE 2. LES LIMITES
Propriété 2 Tout nombre irrationnel peut être approché avec le degré de précision choisi à
l’aide de nombres rationnels qui l’encadrent.
Soit a un nombre irrationnel positif et choisissons de déterminer des valeurs
approchées (par défaut et par excès) de a à 0,001 près.
Il est évident que a est compris entre deux nombres entiers consécutifs n et n + 1.
Représentons ces deux nombres sur la droite graduée et divisons le segment ainsi
obtenu en 10 parties égales.
Le point A représentant a se trouve nécessairement entre deux sous-graduations
qui définissent un nouveau segment : s’il était sur la sous-graduation créée, il
représenterait un nombre rationnel. Les sous-graduations expriment les dixièmes.
A
n
B
a
R
n+1
Divisons le nouveau segment en 10 parties égales et nous obtenons les centièmes.
Le point A ne se trouve toujours pas sur la nouvelle sous-graduation pour la
même raison que précédemment.
A
A0 B 0
a
B
R
En refaisant une troisième fois la même construction, on obtient les millièmes.
A0
A00 B 00
a
B0
R
Propriété 3 Tout nombre réel peut être exprimé avec le degré de précision que l’on veut à l’aide
de nombres rationnels
15
2.3. LIMITES D’UNE VARIABLE
2.3
2.3.1
Limites d’une variable
Limites finies
Considérons une variable réelle x.
x tend vers 5 (x → 5) si x prend des valeurs aussi proches de 5 que l’on veut sans nécessairement l’atteindre 1 . Il en résulte que la "distance" entre x et 5 devient aussi petite que l’on veut,
ce qui se traduit mathématiquement par :
∃η ∈ R+
0 : |x − 5| < η
η est un nombre strictement positif, arbitrairement choisi, aussi petit que l’on veut.
Définition: x tend vers a si x prend des valeurs aussi proches de a que
l’on veut sans nécessairement l’atteindre, ce qui se traduit
mathématiquement par :
x → a ⇔ ∃η ∈ R+
0 : |x − a| < η
η est un nombre strictement positif, arbitrairement choisi,
aussi petit que l’on veut.
4.9
4.99
4.999 5
5.001
5.01
5.1
R
Notons que x peut tendre vers 5 de plusieurs manières :
• x prend successivement des valeurs telles que 4,9 ; 4,99 ; 4,999 ;... il tend vers 5 par la
gauche, c’est-à-dire par valeurs plus petites que 5. Nous dirons qu’il tend vers 5 par valeurs
inférieures et nous écrirons
x → 5−
• x prend successivement des valeurs telles que 5,1 ; 5,01 ; 5,001 ;... il tend vers 5 par la
droite, c’est-à-dire par valeurs plus grandes que 5. Nous dirons qu’il tend vers 5 par valeurs
supérieures et nous écrirons
x → 5+
• x prend successivement des valeurs telles que 4,9 ; 5,01 ; 4,99 ; 5,001 ; 4,999 ; 5,0001 ; ...
2.3.2
Limite infinie
Considérons les valeurs successives de x : 1 ; 10 ; 100 ; 1000 ; ...
Définition: x tend vers plus l’infini si x augmente sans cesse et devient
plus grand que tout nombre positif A arbitrairement choisi,
aussi grand que l’on veut, ce qui s’écrit :
∃A ∈ R+
0 : x > A
1. Voir à ce sujet le paragraphe 2.2.2
16
CHAPITRE 2. LES LIMITES
De même, considérons les valeurs successives de x : -1 ; -10 ; -100 ; -1000 ;...
Définition: x tend vers moins l’infini si x diminue sans cesse, et devient, en valeur absolue, plus grand que tout nombre positif
A arbitrairement choisi, aussi grand que l’on veut, ce qui
s’écrit :
∃A ∈ R+
0 : |x| > A
Remarques importantes • +∞ est un élément qui est strictement supérieur à tout réel ;
• −∞ est un élément qui est strictement inférieur à tout réel ;
• −∞ et +∞ ne sont pas des réels.
Nous ferons toujours précéder le symbole ∞ du signe + ou du signe - pour éviter toute
confusion.
2.4
Limites d’une fonction
Lorsque l’on s’intéresse aux fonctions, plusieurs cas de figure peuvent se présenter selon que
x tende vers une valeur finie ou vers l’infini.
Dans les cas simples, on envisagera :
x tend vers
une valeur finie
une valeur finie
vers ±∞
vers ±∞
f (x) tend vers
une valeur finie
vers ±∞
une valeur finie
vers ±∞
D’autres cas plus complexes peuvent se présenter et seront envisager au paragraphe ??
2.4.1
Limite finie d’une fonction lorsque x tend vers une valeur finie
Approche intuitive
Considérons la fonction f (x) = x2 dont le graphe est représenté à la page suivante.
17
2.4. LIMITES D’UNE FONCTION
On constate que si x tend vers 2 par la gauche (flèche orange), le point dont l’abscisse vaut
x se déplace sur le graphe dans la sens de la flèche vers A et la valeur de la fonction tend vers 4
(sur l’axe Oy dans le sens de la flèche orange).
De même, si x tend vers 2 par la droite (flèche verte), le point dont l’abscisse vaut x se déplace
sur le graphe dans la sens de la flèche vers A et la valeur de la fonction tend vers 4 (sur l’axe Oy
dans le sens de la flèche verte).
On écrira :
lim− x2 = lim+ x2 = lim x2 = 4
x→2
x→2
x→2
Cette notation signifie que "si x tend vers 2 sans jamais atteindre 2, la fonction x2 tend
vers 4 sans jamais atteindre 4 ".
Approche mathématique
Soit la fonction f(x) représentée ci-dessous.
18
CHAPITRE 2. LES LIMITES
Définition: On déduit du graphique précédent :
+
lim f (x) = b ⇔ ∀ ∈ R+
0 , ∃η ∈ R0 : |x − a| < η, |f (x) − b| < x→a
Cette définition signifie que si l’on se choisit un intervalle I donné de taille 2 centré autour
de b, il sera toujours possible de trouver un intervalle de taille 2η centré autour de a et aussi petit
que l’on veut tel que si x est compris dans ce dernier intervalle, f (x) sera compris dans I.
Définition: La limite en a existe si et seulement si
lim f (x) = lim+ f (x) = f (a)
x→a−
2.4.2
x→a
Limites infinie lorsque x tend vers une valeur finie
Approche intuitive
Considérons la fonction f (x) =
1
dont le graphe est représenté ci-dessous.
x−2
On constate que si x tend vers 2 par la gauche (flèche orange), le point dont l’abscisse vaut x
se déplace sur le graphe dans la sens de la flèche et la valeur de la fonction augmente indéfiniment
(sur l’axe Oy dans le sens de la flèche orange).
De même, si x tend vers 2 par la droite (flèche verte), le point dont l’abscisse vaut x se déplace
sur le graphe dans la sens de la flèche et la valeur de la fonction diminue indéfiniment (sur l’axe
Oy dans le sens de la flèche verte).
On écrira :
1
lim−
= −∞
x→2
x−2
et
1
lim+
= +∞
x→2
x−2
19
2.4. LIMITES D’UNE FONCTION
Cette notation signifie que "si x tend vers 2 sans jamais atteindre 2, la fonction
augmente indéfiniment en valeur absolue".
1
x−2
Approche mathématique
Soit la fonction f(x) représentée ci-dessous.
Définition: On déduit du graphique précédent :
+
lim f (x) = +∞ ⇔ ∀A ∈ R+
0 , ∃η ∈ R0 : |x − a| < η, f (x) > A
x→a
et
+
lim f (x) = −∞ ⇔ ∀A ∈ R−
0 , ∃η ∈ R0 : |x − a| < η, f (x) < A
x→a
Cette définition signifie que si l’on se choisit un nombre donné A, il sera toujours possible
de trouver un intervalle de taille 2η centré autour de a tel que si x est compris dans ce dernier
intervalle, f (x) pourra être rendu aussi grand (petit) que l’on veut.
2.4.3
Limite finie lorsque x tend vers une valeur infinie
Approche intuitive
Considérons la fonction f (x) =
1
dont le graphe est représenté à la page suivante.
x−2
20
CHAPITRE 2. LES LIMITES
On constate que si x tend vers +∞ (augmente indéfiniment) (flèche orange), le point dont
l’abscisse vaut x se déplace sur le graphe dans la sens de la flèche et la valeur de la fonction tend
vers 0 (sur l’axe Oy dans le sens de la flèche orange).
De même, si x tend vers −∞ (diminue indéfiniment) (flèche verte), le point dont l’abscisse vaut
x se déplace sur le graphe dans la sens de la flèche et la valeur de la fonction également vers 0
(sur l’axe Oy dans le sens de la flèche verte).
On écrira :
1
=0
lim
x→+∞ x − 2
et
1
lim
=0
x→−∞ x − 2
1
tend vers 0 sans jamais
Cette notation signifie que "si x tend vers ±∞, la fonction
x−2
l’atteindre".
Approche mathématique
Soit la fonction f(x) représentée ci-dessous.
21
2.4. LIMITES D’UNE FONCTION
Définition: On déduit du graphique précédent :
+
lim f (x) = b ⇔ ∀ ∈ R+
0 , ∃B ∈ R0 : x > B, |f (x) − b| < x→+∞
et
−
lim f (x) = b ⇔ ∀ ∈ R+
0 , ∃B ∈ R0 : x < B, |f (x) − b| < x→−∞
Cette définition signifie que si l’on se choisit un intervalle I donné de taille 2 centré autour
de b, il sera toujours possible un nombre B aussi grand (petit) que l’on veut tel que si x est
supérieur (inférieur) à ce nombre, f (x) sera compris dans I.
2.4.4
Limite infinie lorsque x tend vers une valeur infinie
Approche intuitive
Considérons la fonction f (x) = x3 dont le graphe est représenté ci-dessous.
On constate que si x tend vers +∞ (augmente indéfiniment) (flèche orange), le point dont
l’abscisse vaut x se déplace sur le graphe dans la sens de la flèche et la valeur de la fonction
augmente indéfiniment (sur l’axe Oy dans le sens de la flèche orange).
De même, si x tend vers −∞ (diminue indéfiniment) (flèche verte), le point dont l’abscisse vaut x
se déplace sur le graphe dans la sens de la flèche et la valeur de la fonction diminue indéfiniment
(sur l’axe Oy dans le sens de la flèche verte).
On écrira :
lim x3 = +∞
x→+∞
et
lim x3 = −∞
x→−∞
Cette notation signifie que "si x augmente (diminue) indéfiniment, la fonction x3 augmente (diminue) indéfiniment".
22
CHAPITRE 2. LES LIMITES
Approche mathématique
Soit la fonction f(x) représentée cidessous.
Définition: On déduit du graphique précédent :
+
lim f (x) = +∞ ⇔ ∀A ∈ R+
0 , ∃B ∈ R0 : x > B, f (x) > A
x→+∞
et
−
lim f (x) = −∞ ⇔ ∀A ∈ R−
0 , ∃B ∈ R0 : x < B, f (x) < A
x→−∞
De même, on pourra également écrire :
+
lim f (x) = −∞ ⇔ ∀A ∈ R−
0 , ∃B ∈ R0 : x > B, f (x) < A
x→+∞
et
+
lim f (x) = +∞ ⇔ ∀A ∈ R−
0 , ∃B ∈ R0 : x < B, f (x) > A
x→−∞
Cette définition signifie que si l’on se choisit un nombre donné A, il sera toujours possible de
trouver un nombre B tel que si x est supérieur (inférieur) à ce nombre, f (x) pourra être rendu
aussi grand (petit) que l’on veut.
23
2.5. OPÉRATIONS SUR LES LIMITES
2.5
Opérations sur les limites
On admettra sans démonstration les propriétés suivantes :
lim (f (x) + g(x)) = lim f (x) + lim g(x)
x→a
x→a
x→a
lim (f (x) − g(x)) = lim f (x) − lim g(x)
x→a
x→a
x→a
lim (f (x).g(x)) = lim f (x). lim g(x)
x→a
x→a
x→a
lim f (x)
f (x)
x→a
=
lim
x→a g(x)
lim g(x)
x→a
lim (k.f (x)) = k. lim f (x)
x→a
lim
x→a
x→a
q
p
n
f (x) = n lim f (x)
x→a
Remarquons que a peut prendre une valeur finie ou infinie. L’ensemble des résultats des opérations sur les limites est résumé dans le tableau suivant.
Dans ce tableau P (x) et Q(x) représentent des expressions polynomiales, I(x) et J(x) des expressions irrationnelles, r un nombre réel et m un nombre réel non nul.
lim f (x) où a est adhérent au domaine
x→a
f (x) = P (x) ou
f (x) = I(x)
lim f (x) = f (a)
x→a
f (x) =
P (x)
Q(x)
I(x)
P (x)
ou f (x) =
ou
Q(x)
J(x)
I(x)
f (x) =
J(x)
f (x) =
lim f (x) = r si Q(a) 6= 0
m
= ±∞ (le signe est
0
lim f (x) = r si Q(a) 6= 0 ou J(a) 6=
0
m
lim f (x) =
= ±∞ (T.S.)
x→a
0
0
F.I. à lever (voir para0
x→a
x→a
lim f (x) =
x→a
x→a
déterminé par un tableau de signe)
lim f (x) =
x→a
graphe ??)
lim f (x) =
0
F.I. à lever
0
Remarque Un point adhérent à un domaine de définition est une valeur ponctuelle de x rejetée
du domaine mais telle que lim− f (x) et/ou lim− f (x) peuvent être calculée.
x→a
x→a
24
CHAPITRE 2. LES LIMITES
lim f (x) où ±∞ est adhérent au domaine.
x→±∞
f (x) = P (x) ou
f (x) = I(x)
lim f (x) = ±∞
x→±∞
f (x) =
P (x)
Q(x)
lim f (x) =
x→a
m
=0
±∞
lim f (x) =
x→±∞
I(x)
P (x)
ou f (x) =
ou
Q(x)
J(x)
I(x)
f (x) =
J(x)
f (x) =
±∞
F.I. à lever
±∞
lim f (x) =
m
=0
±∞
lim f (x) =
±∞
F.I. à lever
±∞
x→±∞
x→±∞
lim f (x) = ∞ − ∞ F.I. à lever
x→±∞
Remarque Détermination du signe de l’infini
Ce problème ne se pose que lors du calcul de la limite d’une fraction dont le
dénominateur tend vers 0 (quand x tend vers une limite finie a) ou dans le
cas de certaines indéterminations. Une étude de signe de la fonction permet
immédiatement de déterminer le signe de l’infini.
2.6
Cas d’indétermination
Bien qu’il en existe d’autres, nous n’envisagerons que les quatre cas d’indétermination suivants :
0
•
0
∞
•
∞
• ∞−∞
• 0.∞
Le dernier cas est surtout théorique, car il peut facilement se ramener à un des deux premiers
en tenant compte du fait que diviser par un nombre, c’est multiplier par son inverse. Il sera traité
exclusivement en 6ème année.
Il reste donc en pratique trois cas à étudier. Ces cas d’indétermination seront étudiés sur base
d’exemples détaillés.
25
2.6. CAS D’INDÉTERMINATION
2.6.1
Cas
0
0
1. Calculer lim
x→1
On obtient :
x2 − 4x + 3
.
x2 − 3x + 2
x2 − 4x + 3
0
=
F.I.
x→1 x2 − 3x + 2
0
Dans ce cas de figure, le numérateur et le dénominateur de la fraction s’énnulent pour x = 1.
Le numérateur et le dénominateur sont donc divisible par (x − 1) et donc factorisable 2 . On
a:
x−3
(x − 1)(x − 3)
= lim
=2
lim
x→1 x − 2
x→1 (x − 1)(x − 2)
√
x+1−2
2. Calculer lim √
.
x→3
x−3
On obtient :
√
x+1−2
0
F.I.
lim √
=
x→3
0
x−3
La présence du facteur commun est moins visible que dans le cas précédent. Pour le voir
apparaître plus clairement, on rationnalise le numérateur ET le dénominateur. On a :
√
√
√
√
x+1−2
x+1−2
x−3
x+1+2
√
√
lim √
= lim √
x→3
x→3
x−3
x−3
x−3
x+1+2
lim
et, après simplifications :
√
√
x+1−4
x−3
x−3
√
lim
= lim √
=0
x→3
x−3
x + 1 + 2 x→3 x + 1 + 2
2. D’après la loi du reste vue en 3ème
26
CHAPITRE 2. LES LIMITES
2.6.2
Cas
∞
∞
1. Calculer lim
x→±∞
On obtient :
x2 − 1
.
2x2 + 3x + 2
x2 − 1
∞
=
F.I.
2
x→±∞ 2x + 3x + 2
∞
Factorisons l’expression dans la limite en mettan en évidence les termes de plus haut degré.
On a :
1
2
x 1− 2
x
lim
x→±∞
3
2
2
2x 1 +
+
2x 2x2
lim
1
1
Les termes en et 2 sont quasi nul lorsque x tend vers ±∞ et sont donc négligeables par
x
x
rapport aux termes unités. La limite devient donc :
lim
x→±∞
2. Calculer lim
x→±∞
On obtient :
√
x2
1
1
=
= lim
2
x→±∞
2x
2
2
4x − 1
.
+ 5x + 3
x2
4x − 1
∞
=
F.I.
x→±∞
∞
+ 5x + 3
En effctuant la même opération que dans l’exemple ci-dessus :
1
4x 1 −
4x
lim s x→±∞
5x
3
2
x 1+ 2 + 2
x
x
lim
En négligeant les termes en
√
x2
1
1
et 2 , on obtient :
x
x
lim
x→±∞
4x
4x
√ = lim
x2 x→±∞ |x|
On doit, contrairement au cas précédent, scinder la limite en deux parties. On a :
lim
x→+∞
et
lim
x→−∞
4x
=4
x
4x
= −4
−x
27
2.6. CAS D’INDÉTERMINATION
2.6.3
Cas ∞ − ∞
Calculer lim
√
x→±∞
x+1−
√
2x + 1 .
Remarquons que, en raison du domaine de définition de la fonction, la limite en −∞ n’existe pas.
On a :
i
h√
√
x + 1 − 2x + 1 = ∞ − ∞ F.I.
lim
x→+∞
En rationnalisant cette expression, on obtient :
√
√
√
√
x + 1 − 2x + 1 . x + 1 + 2x + 1
√
√
lim
x→+∞
x + 1 + 2x + 1
ou, en simplifiant :
lim
x→+∞
(x + 1) − (2x + 1)
−x
∞
√
= lim √
=
√
√
x→+∞
∞
x + 1 + 2x + 1
x + 1 + 2x + 1
F.I.
On est ramené au cas du paragraphe 2.6.2. On a :
lim
x→+∞
√
−x
−x
= lim s √
s x→+∞
x + 1 + 2x + 1
1
1
x 1+
+ 2x 1 +
x
2x
En négligeant les termes en
1
1
et 2 , on obtient :
x
x
lim
x→+∞
ou en rationnalisant :
lim
x→+∞
√
−x
−x
√ = lim √
√ x + 2x x→+∞ x 1 + 2
√
√
−x x
− x
√ = lim
√ = −∞
x→+∞ 1 +
x 1+ 2
2
28
CHAPITRE 2. LES LIMITES
2.7
Exercices
1. Déterminer graphiquement les limites en a suivantes. Le cas échéant, déterminer la limite à
gauche et la limite à droite.
(a) a = −2, −1, 0, 2
(b) a = ±∞
(e) a = −∞, −3, −2, −1, 0, 1, 3, +∞
(c) a = −3, −2, 1, 2, 3
(d) a = ±∞
29
2.7. EXERCICES
2. Calculer les limites suivantes. Dans le cas de limites infinies, spécifier si les fonctions tendent
vers +∞ ou −∞
x2 + 2x + 5
x→1
x2 + 1
2−x
(b) lim √
x→2
2+x
x3 + 5x2 − x − 3
(c) lim
x→−2
x2 − 3x + 4
−3
(d) lim
x→2 (x − 2)2
(a) lim
x+2
√
x + x2 + x + 3
(e) lim
x→−3
(f) lim (x2 + 5x + 2)
x→+∞
(g) lim
x→−∞
(h) lim
x→+∞
3x2 − x + 2
4
5
x−5
3. Calculer les limites suivantes
x3 − 1
x→1 x − 1
4x3 − 2x2 + x
(b) lim
x→0
3x2 + 2x
x2 + 3x − 10
(c) lim
x→2 3x2 − 5x − 2
x3 − x2 − x + 1
(d) lim
x→−1
x2 + 2x + 1
(a) lim
|x + 1|
x→−1 x + 1
√
1+x−1
(f) lim
x→0
x
√
x2 + x + 1 − 1
(g) lim
x→0
x
√
2x + 1 − 3
√
(h) lim √
x→4
x−2− 2
(e) lim
4. Calculer les limites suivantes
(a) lim
x→±∞
(b) lim
x→±∞
(c) lim
x→±∞
4x3 − 2x2 + 1
x2 − 1
4x3 − 2x2 + 1
3x3 + 5
4x3 − 2x2 + 1
x4 − 1
5. Calculer les limites suivantes
√
(a) lim
x2 + 1 − x + 1
x→±∞
√
(b) lim x x2 + 1 − x
x→±∞
(d) lim
x→±∞
(e) lim
x→±∞
(f) lim
x→±∞
(c) lim
4x + 1
√
2
x + 5x + 3
2x
√
2x2 − 2x
x+1
√
2
x −4−x
√
x2 − x − x
x→±∞
√
(d) lim 3x + 1 − 9x2 − 3x
x→±∞
6. Calculer les limites suivantes (cas mélangés)
8x3 + 2x2 − 5x + 1
x→±∞ 8x3 + 10x2 − 11x + 2
x+4
x−6
(b) lim
−
x→0
x2 − 4 x(x − 2)
(a) lim
2
2
2x + bx − b
,b∈R
x→±∞ x2 + 2bx + b2
x+4
x−6
(d) lim
−
x→2
x2 − 4 x(x − 2)
x+4
x−6
(e) lim
−
x→±∞
x2 − 4 x(x − 2)
(c) lim
(f) lim
2x2 + bx − b2
,b∈R
x2 + 2bx + b2
(g) lim1
8x3 + 2x2 − 5x + 1
8x3 + 10x2 − 11x + 2
x→−b
x→ 2
1
x+1
(h) lim
x
x→0
x−
x−1
x+1
(i) lim √
x→±∞
x2 + 2x + 2 − 1
5+
30
CHAPITRE 2. LES LIMITES
(j)
(k)
(l)
(m)
(n)
1
5+
x+1
lim
x
x→1
x−
√ x−1
x+4−2
lim
x→0
x
1
5+
x+1
lim
x
x→2
x−
x−1
8x3 + 2x2 − 5x + 1
lim
3
2
x→ 14 8x + 10x − 11x + 2
1
5+
x+1
lim
x
x→±∞
x−
x−1
(o) lim
x→±∞
√
x+4−2
x
√
x−1
(p) lim √
3
x→1
x−1
x+1
x→−1
x2 + 2x + 2 − 1
√
(r) lim 3x − 9x2 − x − 4
(q) lim √
x→±∞
(s) lim
x→0
(t) lim
8x3 + 2x2 − 5x + 1
8x3 + 10x2 − 11x + 2
x→±∞
2x
√
2x − 3 + x2 − 2x + 3
Chapitre 3
Les asymptotes
3.1
Définition
Définition: Une droite asymptote (ou plus simplement asymptote) à
une courbe est une droite telle que, lorsque l’abscisse ou
l’ordonnée d’un point de la courbe tend vers l’infini, la
distance de la courbe à la droite tend vers 0 a .
a. Le calcul des asymptote est donc intimement lié à celui des limites
On parle parfois de branche infinie ou de comportement à l’infini de la fonction. Une asymptote est utilisée dans certaines sciences pour prédire le comportement à long terme d’une grandeur.
Un asymptote peut être une courbe quelconque (et pas seulement une droite). Ainsi, par
exemple, le "trident de Newton", courbe représentative de la fonction :
f (x) =
ax3 + bx2 + cx + d
x
admet deux courbes asymptotes : une parabole d’équation ax2 +bx+c et une hyperbole d’équation
d
x
Figure 3.1 – Graphe de la fontion
x3 + 1
x
Cependant, dans le cadre de ce cours, nous nous limiterons aux droites asymptotes.
31
32
CHAPITRE 3. LES ASYMPTOTES
3.2
Point adhérent au domaine
Définition: Le point a est adhérent à domf si tout intervalle centré en
a possède un point dans domf . On a :
∀r ∈ R+
0 :]a − r, a + r[∩domf 6= φ
1
, le point 1 est adhérent au domaine R\{1}
x√− 1
• Soit la fonction f (x) = x2 − 1, le point 1 est adhérent au domaine −∞, −1] ∪
[1, +∞ mais le point 0 ne l’est pas.
Exemples • Soit la fonction f (x) =
3.3
Asymptotes verticales
Considérons le graphe de la fonction f (x) =
x−2
.
x+3
Le domaine de définition de la fonction ci-dessus est R\ {−3}
A l’aide du calcul des limites, on peut constater que si x tend vers -3, la fonction tendra vers
l’infini. Graphiquement, on constate la présence d’une asymptote verticale en x = −3
Définition: La droite d’équation x = a est une asymptote verticale (en
abrégé AV) de la courbe d’équation y = f (x) si et seulement
si :
lim f (x) = ±∞
x→a
Les points (valeurs de x) où la courbe est susceptible de
présenter une AV sont les points adhérents au domaine de
définition a
a. c’est-à-dire les valeurs "ponctuelles"(ne correspondant pas à un intervalle de valeurs) rejettées du domaine de définition de la fonction.
33
3.3. ASYMPTOTES VERTICALES
3.3.1
Premier exemple
Considérons la fonction
f (x) =
x2
2x − 1
− 3x + 2
Le domaine de définition de la fonction est R\ {1, 2}. Les valeurs ponctuelles rejetées du
domaine sont donc x = 1 et x = 2.
Calculons la limite de la fonction pour ces deux valeurs de x. On a :
lim
2x − 1
= ±∞
x2 − 3x + 2
lim
2x − 1
= ±∞
− 3x + 2
x→1
et
x→2 x2
La courbe représentative de f (x) présente donc deux asymptotes verticales d’équation
AV1 ≡ x = 1
et
AV2 ≡ x = 2
comme le montre le graphe suivant
3.3.2
Deuxième exemple
Considérons la fonction
f (x) =
x2
x−1
− 3x + 2
Comme dans l’exemple précédent, on a domf : R\ {1, 2}. Les valeurs ponctulles rejetées du
domaine sont donc x = 1 et x = 2.
Calculons la limite de la fonction pour ces deux valeurs de x. On a :
lim
x→1 x2
= lim
x→1
x−1
0
= F.I.
− 3x + 2
0
1
x−1
= lim
= −1
(x − 1)(x − 2) x→1 x − 2
34
CHAPITRE 3. LES ASYMPTOTES
et
lim
x→2 x2
2x − 1
= ±∞
− 3x + 2
La courbe représentative de f (x) présente donc une seule asymptote verticale d’équation
AV ≡ x = 2
3.3.3
Troisème exemple
Considérons la fonction
f (x) =
2x − 1
x2 + 2
Le domaine de cette fonction étant R, il n’y aucune asymptote verticale.
3.3.4
Remarque importante
Dans le cadre de ce paragraphe, nous nous sommes intéressés uniquement aux asymptotes
verticales. Il est claire que les différentes présentent d’autres asymptotes 1 . Nous les étudierons
dans les paragraphes suivants.
1. Comme le montre les graphiques
35
3.4. ASYMPTOTES HORIZONTALES
3.4
Asymptotes horizontales
Les asymptotes horizontales concernent l’étude du comportement à l’infini de la fonction,
c’est-à-dire lorsque la variable x tend vers ±∞. Elle permet de prédire le comportement de la
fonction en dehors de la zone représentée sur papier.
Reprenons le graphe de la fonction f (x) =
x−2
.
x+3
On constate graphiquement que si x tend vers ±∞, le graphe de la fonction tend vers 1.
Définition: La droite d’équation y = b est une asymptote horizontale
(en abrégé AH) de la courbe d’équation y = f (x) si et seulement si :
lim f (x) = b
x→±∞
Remarquons que, pour pouvoir déterminer une éventuelle asymptote horizontale, il faut que
±∞ appartiennent au domaine de définition de la fonction.
3.4.1
Premier exemple
Considérons la fonction
f (x) =
2x − 1
x2 − 3x + 2
Le domaine de définition de f (x) contient ±∞. Le calcul des AH est donc possible. On a :
lim
x→±∞ x2
= lim
x→±∞
2x − 1
∞
=
F.I.
− 3x + 2
∞
2x
2
=
lim
=0
x→±∞ x
x2
La fonction présente donc une asymptote horizontale d’équation
AH ≡ y = 0
36
CHAPITRE 3. LES ASYMPTOTES
3.4.2
Deuxième exemple
Considérons la fonction
√
x2 − 5
f (x) =
x+2
Le domaine de définition de f (x) contient ±∞. Le calcul des AH est donc possible. On a :
√
∞
x2 − 5
=
F.I.
lim
x→±∞
x+2
∞
√
|x|
x2
= lim
= lim
x→±∞
x→±∞ x
x
Vu la présence de la valeur absolue, il faut séparer le calcul de la limite en deux parties. On a :
lim
x→−∞
lim
−x
= −1
x
x→+∞
x
=1
x
Dans ce cas-ci, on a deux asymptotes horizontales 2 :
AHg ≡ y = −1
AHd ≡ y = 1
2. Les labels
g
et
d
signifie respectivement "à gauche" (−∞) et "à droite" (+∞)
37
3.4. ASYMPTOTES HORIZONTALES
3.4.3
Troisième exemple
Considérons la fonction
f (x) =
√
1 − x2
Le domaine de définition de la fonction ne contient pas ±∞. Il n’y a donc pas d’asymptote
horizontale.
3.4.4
Remarque importante
Dans le cadre de ce paragraphe, nous nous sommes intéressés uniquement aux asymptotes
horizontales. Il est claire que les différentes présentent d’autres asymptotes. Nous les étudierons
dans les paragraphes suivants.
38
CHAPITRE 3. LES ASYMPTOTES
3.5
Asymptotes obliques
Une asymptote oblique est une droite d’équation générale
AO ≡ y = mx + p
Soit la fonction f (x) dont le graphe est représenté ci-dessous.
Choisissons un point A(x, y) sur le graphique de cette fonction et faisons tendre x vers +∞.
Le point A s’éloignera vers l’infini et son ordonnée deviendra aussi de plus en plus grande. Dans
le cas présent, on a :
lim f (x) = +∞
x→+∞
et
lim f (x) = −∞
x→−∞
Dès lors, si une fonction admet un asymptote oblique, elle n’admettra pas d’asymptote
horizontale et inversément.
On a :
|AB| = |f (x) − (mx + p)|
(3.5.1)
Puisque cette longueur tend vers 0 quand x tend vers l’infini (par définition d’une asymptote),
on a :
lim [f (x) − (mx + p)] = 0
x→+∞
ce qui entraîne
f (x) − (mx + p)
=0
x→+∞
x
car x est différent de 0, quand il tend vers l’infini et donc
f (x)
p
lim
− (m + ) = 0
x→+∞
x
x
lim
39
3.5. ASYMPTOTES OBLIQUES
Définition: Une asymptote oblique est une droite d’équation générale
AO ≡ y = mx + p
où
m = lim
x→+∞
f (x)
x
et
p = lim [f (x) − mx]
x→+∞
Les relations permettant de calculer le coefficient angulaire
et l’ordonnée à l’origine d’une asymptote oblique sont appelées les "formules de Cauchy"
3.5.1
Remarque concernant le calcul des asymptotes horizontales et
obliques
Le calcul des asympotes horizontales et obliques passe par des calcul de limites en ±∞ et
∞
.
amène parfois à devoir lever des indéterminations du type
∞
D’après ce qui a été vu au paragraphe 2.6, il ressort que :
• Si le degré du numérateur de la fonction et inférieur ou égale à celui du dénominateur la
fonction admettra une asymptote horizontale ;
• Si le degré du numérateur est supérieur d’une unité au degré du dénominateur, la fonction
admettra une asymptote oblique ;
• dans tous les autres cas, elle n’admettra aucune asymptote, ni horizontale, ni verticale.
Dans le cas de calcul de limites en ±∞ amenant à des indéterminations du type ∞ − ∞, la
conclusion est moins évidente à tirer.
De plus, et uniquement dans le cas de fonctions rationnelles, le calcul de l’asympote peut se
faire à l’aide de la division euclidienne. Cette technique, qui sera développée dans les exemples
(voir paragraphe 3.5.2) est beaucoup plus rapide que l’application des formules et permet en outre
d’obtenir des informations conmplémentaires concernant la position de la courbe par rapport aux
asymptotes (voir à ce sujet le paragraphe 3.6)
3.5.2
Premier exemple
Considérons la fonction
f (x) =
2x3 − 1
x2 − 3x + 2
Cette fonction rationnelle présente un degré du numérateur est supérieur d’une unité au degré
du dénominateur, la fonction admettra une asymptote oblique.
40
CHAPITRE 3. LES ASYMPTOTES
Les formules de Cauchy donnent :
m = lim f (x).
x→±∞
1
2x3 − 1
∞
= lim
=
F.I.
x x→±∞ x3 − 3x2 + 2x
∞
= lim
x→±∞
et
p = lim
x→±∞
2x3
=2
x3
2x3 − 1
2x3 − 1 − 2x3 + 6x2 − 4x
−
2x
=
lim
x→±∞
x2 − 3x + 2
x2 − 3x + 2
= lim
x→±∞
∞
6x2 − 4x − 1
=
F.I.
2
x − 3x + 2
∞
6x2
= lim
=6
x→±∞ x2
La fonction admet une asymptote oblique d’équation
AO ≡ y = 2x + 6
Pour la trouver d’une autre manière, effectuons la division euclidienne. On a :
2x3
−1 x2 − 3x + 2
2x3 −6x2 +4x
2x + 6
2
6x
−4x
6x2 −18x +12
14x −13
La fonction s’écrit donc :
14x − 13
x2 − 3x + 2
14x − 13
Analysons cette fonction. Si x tend vers ±∞, la fraction 2
tend vers 0 en raison de
x − 3x + 2
l’explication donnée au paragraphe 3.5.1. Si x tend vers ±∞, la fonction tend vers la droite
d’équation y = 2x + 6 qui, par définition d’une asymptote, est une asymptote oblique de la
fonction 3 .
f (x) = 2x + 6 +
3. voir paragraphe 3.1
41
3.5. ASYMPTOTES OBLIQUES
3.5.3
Deuxième exemple
Considérons la fonction
f (x) =
√
x2 − 1
Cette fonction rationnelle présente un degré du numérateur est supérieur d’une unité au degré
du dénominateur, la fonction admettra une asymptote oblique.
Par contre, dans ce cas-ci, il n’est plus possible de trouver l’équation de l’asymptote par division
euclidienne. Il faut donc appliquer les formules de Cauchy. On a :
√
x2 − 1
∞
1
=
F.I.
m = lim f (x). lim
x→±∞
x x→±∞
x
∞
En levant l’indétermination conformément aux prescriptions du paragraphe 2.6.2, on obtient :
m = 1 en + ∞
et
m = −1 en − ∞
De plus, on trouve aisément que
p=0
Dans ce cas-ci, on a deux asymptotes obliques :
AOg ≡ y = −x
AOd ≡ y = x
3.5.4
Remarque importante
Dans le cadre de ce paragraphe, nous nous sommes intéressés uniquement aux asymptotes
horizontales. Il est claire que les différentes présentent d’autres asymptotes.
42
CHAPITRE 3. LES ASYMPTOTES
3.6
Position d’une courbe par rapport à une asymptote
Afin de pouvoir dessiner complètement le graphe d’une fonction, il est encore important de
connaître la position de la courbe par rapport aux asymptotes.
L’étude de cette position consiste à dire
• si la courbe représentative de la fonction tend vers ±∞ l’infini au voisinage d’une asymptote
verticale ;
• si la courbe représentative de la fonction est située au-dessus ou sous les asymptotes horizontales et/ou obliques.
La position de la courbe par rapport à une asymptote verticale s’effectue à l’aide d’un simple
tableau de signe de la fonction autour de x = a 4 .
L’étude de la position de la courbe par rapport aux asymptotes horizontales et obliques passe
par le calcul du signe de la distance entre la courbe et l’asymptote.
Définissons cette distance par :
d(x) = f (x) − yasymptote
comme le montre la figure suivante
Sur cette figure [AB] représente la distance d(x), [AC] la fonction f (x) et [BC], yasymptote .
Si cette distance est positive, la fonction est située au dessus de l’asymptote. Si elle est négative,
elle est sous l’asymptote.
Exemple Reprenons la fonction
2x3 − 1
x2 − 3x + 2
Cette fonction admet deux asymptotes verticales en x = 1 et x = 2 et une asymptote
oblique d’équation y = 2x + 6.
Etudions la position de la courbe par rapport aux asymptotes.
f (x) =
4. point où il y a une asympote verticale
43
3.6. POSITION D’UNE COURBE PAR RAPPORT À UNE ASYMPTOTE
Exemple
L’étude du signe de la fonction donne :
x
−∞
2x3 − 1
−
2
x − 3x + 2
+
f (x)
−
√
3
4
2
0
0
1
+
+
+
0
|−∞
+∞
2
+
−
−
0
|+∞
−∞
+∞
+
+
+
On a donc
2x3 − 1
= +∞
x→1
x2 − 3x + 2
3
2x − 1
lim+ 2
= −∞
x→1
x − 3x + 2
3
2x − 1
lim− 2
= −∞
x→2
x − 3x + 2
2x3 − 1
lim+ 2
= +∞
x→2
x − 3x + 2
Pour l’asymptote oblique, calculons la distance entre la courbe et l’asympote. On a :
lim−
d(x) =
2x3 − 1
− (2x + 6)
x2 − 3x + 2
Après réduction au même dénominateur, réduction et simplification, on obtient :
d(x) =
14x − 13
− 3x + 2
x2
Cette fonction tend vers 0 si x tend vers ±∞ (par définition d’une asymptote). L’étude
du signe de cette distance donne :
x
−∞
14x − 13
−
2
x − 3x + 2
+
f (x)
−
13
14
0
0
1
+
+
+
0
|−∞
+∞
2
+
−
−
0
|+∞
−∞
+∞
+
+
+
On constate qu’en −∞ la fonction est sous l’asymptote, en +∞ elle est au dessus de
l’asympote.
La figure suivante met en évidence ces résultats.
44
CHAPITRE 3. LES ASYMPTOTES
Exemple Remarquons que, par la division euclidienne effectuée au paragraphe 3.5.2, la distance
apparaît immédiatement dans l’écriture simplifiée de la fonction :
f (x) = 2x + 6 +
14x − 13
− 3x + 2
x2
3.7. EXERCICES
3.7
45
Exercices
Pour les fonctions suivantes, déterminer
• le domaine de définition ;
• les zéros ;
• l’intersection avec l’axe Oy ;
• le signe ;
• les asymptotes éventuelles ainsi que la position relative de la courbe par rapport aux
asymptotes.
1 − 6x
2x − 5
x2 − 4x + 3
f (x) =
2x + 3
r
x−1
f (x) =
x+1
3x2 + 3x
f (x) = 2
x − 3x − 4
r
x2 − x − 1
f (x) =
−1 + 4x2
√
√
f (x) = x2 − 4 − x2 − 1
√
f (x) = x − x2 − 1
x
f (x) = √
1 − x2
1. f (x) =
2.
3.
4.
5.
6.
7.
8.
x−
√
√
x2 − 1
x
1 − x2
x2 − 1
x2 − 4 −
x2 − x − 1
−1 + 4x2
]−1, 1[
−∞, −1] ∪ [1, +∞
−∞, −2] ∪ [2, +∞
0
/
/
√
1± 5
2
√ # 1− 5
1 1
−∞,
∪ − ,
2
2 2
"
√
1+ 5
∪
, +∞
2
r
f (x) = √
√
0
R\ {−1, 4}
x2
3x2 + 3x
− 3x − 4
1
1,3
−∞, −1[ ∪ [1, +∞
x−1
x+1
r
3
R\ −
2
1
6
5
R\
2
1 − 6x
2x − 5
1
5
0
/
/
1
0
/
1
−
∩Oy
1
2
x = ±1
/
/
x=±
x→−1
x = 4( lim f (x) =
x = −1
3
2
5
2
x=−
x=
AV
3
)
5
1
2
/
y = 0 en +∞
y=0
y=
y=3
y=1
/
y = −3
AH
/
/
/
/
2x − 11
4
/
y = 2x en −∞
y=
/
AO
r
3
4
/
d(x)≥ 0 en +∞
et d(x)≤ 0 en −∞
d(x)≤ 0 toujours
d(x)≥ 0 si x ≤ −
12
≥ 0 si x > 4
x−4
x−1
− 1 ≥ 0 si x < −1
x+1
3
45
≥ 0 si x > −
4(2x + 3)
2
5
14
≥ 0 si x <
5 − 2x
2
d(x)
3.8
x2 − 4x + 3
2x + 3
zéro(s)
domf
f (x)
46
CHAPITRE 3. LES ASYMPTOTES
Solutions des exercices
Chapitre 4
Les dérivées
4.1
4.1.1
Rappels
Accroissements et taux d’accroissement
Soit un fonction f (x) continue sur un intervalle I.
Considérons deux valeurs données x1 et x2 de la variable x ⊂ I, auxquelles correspondent deux
valeurs f (x1 ) et f (x2 ) de la fonction.
Figure 4.1 – Accroissement
47
48
CHAPITRE 4. LES DÉRIVÉES
Définition: On définit :
• l’accroissement ∆x de la variable x :
∆x = x2 − x1
• l’accroissement ∆f de la fonction f (x)
∆f = f (x2 ) − f (x1 )
Le taux d’accroissement t de la fonction est le rapport entre
les accroissements ∆f et ∆x. Il s’agit donc du quotient :
α=
4.1.2
∆f
∆x
Coefficient angulaire d’une droite
Le coefficient angulaire (ou coefficient de direction) de la droite d’équation y = mx + p
est m.
Le coefficient angulaire m de la droite passant par les points A(xA , yA ) et B(xB , yB ) est donné
par :
yB − yA
m=
xB − xA
C’est le taux d’accroissement de la fonction f (x) = mx + p L’équation de la droite de coefficient
angulaire m donné et passant par le point A(xA , yA ) s’écrit :
y − yA = m(x − xA )
4.1.3
Sécante à une courbe
On considère une courbe C d’équation y = f (x) et deux points A et B situés sur cette courbe.
La droite AB est sécante à la courbe C.
Une droite est sécante à une courbe lorsqu’elle coupe cette courbe.
Figure 4.2 – Sécante à une courbe
49
4.2. NOMBRE DÉRIVÉ ET FONCTION DÉRIVÉE
4.1.4
Tangente à une courbe
Si les points A et B sont confondus, la droite s devient tangente à la courbe. C’est ce qui
arrive notamment lorsque A reste fixe et que B se déplace sur la courbe vers A jusqu’à être
confondu avec A.
Figure 4.3 – Tangente à une courbe
Conséquence Lorsque l’un des deux points d’intersection de la courbe et de la sécante se
rapproche de l’autre jusqu’à être confondu avec celui-ci, la sécante porte le nom
de tangente.
Il résulte de cette définition que le coefficient angulaire de la tangente t à une
courbe C en un point A est la limite du coefficient angulaire d’une sécante s
comprenant le point A lorsque le point B tend vers A.
mt = lim ms
B→A
4.2
Nombre dérivé et fonction dérivée
Considérons une fonction f (x), continue sur un intervalle donné I du domaine de définition.
4.2.1
Exemple introductif
Considérons la fonction f (x) = x2 et le point A(2,4) situé sur la courbe C représentant cette
fonction. On cherche à déterminer le coefficient angulaire de la tangente à la courbe C au point
A.
A cet effet, choisissons un autre point B(x, x2 ) quelconque, mais situé également sur la courbe C.
50
CHAPITRE 4. LES DÉRIVÉES
Le coefficient angulaire de la sécante s est
ms =
x2 − 4
x−2
Lorsque B se déplace sur la courbe C en direction de A, ce coefficient angulaire varie, mais
l’expression qui permet de le calculer reste inchangée.
Quand B s’approche de A, la droite s s’approche de la tangente et lorsque B arrive en A, s est
confondue avec la tangente t.
Le coefficient angulaire de la tangente est la limite de l’expression ci-dessus lorsque x tend vers 2.
On constate (graphiquement) que le coefficient angulaire de la tangente t vaut 4.
Algébriquement, ce coefficient angulaire vaut :
mt = lim ms = lim
x→2
x→2
0
x2 − 4
= FI
x−2
0
(x − 2)(x + 2)
=4
x−2
On dit que 4 est le nombre dérivé de la fonction x2 en x = 2. On notera :
= lim
x→2
f 0 (2) = 4
De la même façon, calculons f 0 (−1). On a :
f 0 (−1) = lim
x→−1
= lim
x→−1
0
x2 − 1
= FI
x+1
0
(x − 1)(x + 1)
= −2
x+1
On peut ainsi calculer le coefficient angulaire de la tangente t à la courbe d’équation y = f (x)
en n’importe quel point d’abscisse a donnée. En effet, on a
f 0 (a) = lim
x→a
= lim
x→a
x 2 − a2
0
= FI
x−a
0
(x − a)(x + a)
= 2a
x−a
51
4.2. NOMBRE DÉRIVÉ ET FONCTION DÉRIVÉE
4.2.2
Définitions
Définition: On considère la fonction :
f : R 7→ R : x 7→ f (x)
que l’on suppose continue en x = a.
Le nombre dérivé de f (x) en x = a est :
f 0 (a) = lim
x→a
f (x) − f (a)
x−a
si cette limite existe.
La fonction f 0 (x), dérivée de la fonction f (x) est la fonction
qui applique tout point sur le nombre dérivé de f (x) en ce
point :
f 0 : R 7→ R : x 7→ f 0 (x)
Dériver une fonction, c’est rechercher sa fonction dérivée.
Le domaine de dérivabilité d’une fonction est l’ensemble
des réels en lesquels elle est dérivable.
4.2.3
Autre formulation
En appelant ∆x = a − x et la fonction dérivée s’écrit :
f 0 (x) = lim
∆x→0
ou encore
f 0 (x) = lim
∆x→0
4.2.4
f (x) − f (x + ∆x
−∆x
f (+∆x ) − f (x)
∆x
Propriétés
• Une fonction est dérivable en a si et seulement si f 0 (a) est un nombre réel.
• Une fonction est dérivable à gauche en a si et seulement si
f 0 (a) = lim−
x→a
f (x) − f (a)
x−a
existe et est un nombre réel.
• Une fonction est dérivable à droite en a si et seulement si
f 0 (a) = lim+
x→a
f (x) − f (a)
x−a
existe et est un nombre réel.
• Une fonction dérivable à gauche et à droite de a est dérivable en a.
52
4.2.5
CHAPITRE 4. LES DÉRIVÉES
Dérivabilité et continuité
Définition: Soit une fonction f (x) définie sur un intervalle I. Si f (x)
est dérivable sur I, elle est continue sur I.
En effet, si f (x) est dérivable en a, cela signifie que f 0 (a) existe.
De plus, on peut écrire, si x est un point quelconque de I, différent de a :
f (x) = f (a) +
f (x) − f (a)
(x − a)
x−a
et donc,
lim f (x) = lim f (a) + lim
x→a
x→a
x→a
f (x) − f (a)
(x − a)
x−a
ou, en appliquant les propriétés des limites
lim f (x) = f (a) + lim
x→a
ou, puisque lim
x→a
x→a
f (x) − f (a)
. lim (x − a)
x→a
x−a
f (x) − f (a)
= f 0 (a) existe
x−a
lim f (x) = f (a)
x→a
ce qui prouve que la fonction est continue.
Remarque L’inverse n’est pas vrai, un fonction continue n’est pas nécessairement dérivable.
Pour s’en convaincre, il suffit de considérer l’exemple de la fonction f (x) = |x|.
En effet, on a f (0− ) = f (0+ ) = 0 mais f 0 (0− ) = −1 et f 0 (0+ ) = 1
4.3. EQUATION D’UNE TANGENTE À UNE COURBE
4.3
53
Equation d’une tangente à une courbe
S’il existe, le nombre dérivé d’une fonction en un point de celle-ci est le coefficient angulaire
de la tangente à la courbe représentative de cette fonction en ce point.
Définition: L’équation de la tangente au point d’abscisse a s’écrit
t ≡ y − f (a) = f 0 (a)(x − a)
4.4
Formules de dérivation
Dans ce qui suit, nous supposerons que les conditions d’existence sont toutes remplies.
4.4.1
Dérivée d’une constante
Considérons la fonction constante :
f : R 7→ R : x 7→ k k ∈ R
On a :
f (x) − f (a)
k−k
= lim
=0
x→a x − a
x−a
f 0 (a) = lim
x→a
La dérivée d’une constante est nulle. On a :
(k)0 = 0
4.4.2
Fonction identité
Considérons la fonction constante :
f : R 7→ R : x 7→ x
On a :
f 0 (a) = lim
x→a
f (x) − f (a)
x−a
= lim
=1
x→a x − a
x−a
La dérivée de la fonction identité vaut 1. On a :
(x)0 = 1
54
CHAPITRE 4. LES DÉRIVÉES
4.4.3
Puissances entières de x
Considérons la fonction constante :
f : R 7→ R : x 7→ x2
On a :
f 0 (a) = lim
x→a
f (x) − f (a)
x 2 − a2
= lim
= 2a
x→a x − a
x−a
La dérivée de la fonction x est :
2
x2
0
= 2x
De même considérons la fonction constante :
f : R 7→ R : x 7→ x3
On a :
f 0 (a) = lim
x→a
f (x) − f (a)
x 3 − a3
= lim
= 3a2
x→a x − a
x−a
La dérivée de la fonction x3 est :
x3
0
= 3x2
En généralisant, on obtient que la dérivée de la fonction xn (n ∈ N) est :
(xn )0 = nxn−1
Exemples On a les dérivées suivantes :
0
• (x9 ) = 9x8
0
• (x14 ) = 14x13
4.4.4
Racine carrée de x
Considérons la fonction constante :
f : R 7→ R : x 7→
√
On a :
x
√
√
f (x) − f (a)
x− a
0
f (a) = lim
= lim
= FI
x→a
x→a
x−a
x−a
0
√
√ √
√
x− a x+ a
1
√ = √
= lim
.√
x→a
x−a
x+ a
2 a
√
La dérivée de la fonction x est :
0
√ 0
1
x = √
2 x
4.5. OPÉRATIONS SUR LES DÉRIVÉES
4.4.5
55
Puissance quelconque de x
Nous admettrons sans démonstration que a dérivée de la fonction xn (n ∈ R) est :
(xn )0 = nxn−1
√ 0 1 0 1 1
1
Exemples • ( 3 x) = x 3 = x( 3 −1) = √
3
3
3 x2
0 0
1
1
1
1
1
• √
= x− 2 = − x(− 2 −1) = − √
2
x
2 x3
4.5
Opérations sur les dérivées
On considère deux fonctions
f : R 7→ R : x 7→ f (x)
et
g : R 7→ R : x 7→ g(x)
supposée continue. On supposera dans la suite que toutes les conditions d’existence sont vérifiées
4.5.1
Dérivée d’une somme de fonctions
On a :
(f + g)(x) − (f + g)(a)
x→a
x−a
(f (x) + g(x)) − (f (a) + g(a))
= lim
x→a
x−a
(f (x) − f (a)) + (g(x) − g(a))
= lim
x→a
x−a
= f 0 (a) + g 0 (a)
(f + g)0 (a) lim
La dérivée de la somme de deux fonctions est la somme des dérivées.
(f (x) + g(x))0 = f 0 (x) + g 0 (x)
De même, on démontre que la dérivée de la différence de deux fonctions est la différence des
dérivées.
(f (x) − g(x))0 = f 0 (x) − g 0 (x)
Exemples • (x2 + x4 )0 = (x2 )0 + (x4 )0 = 2x + 4x3
√
1
• ( x − x3 ) = √ − 3x2
2 x
56
CHAPITRE 4. LES DÉRIVÉES
4.5.2
Dérivée d’un produit de fonctions
On a :
(f.g)0 (a) lim
x→a
(f.g)(x) − (f.g)(a)
x−a
= lim
x→a
(f (x).g(x)) − (f (a).g(a))
x−a
(f (x).g(x) − f (a).g(x)) + (f (a).g(x) − f (a).g(a))
x−a
(f (a).g(x) − f (a).g(a))
(f (x).g(x) − f (a).g(x))
+ lim
= lim
x→a
x→a
x−a
x−a
= lim
x→a
= lim
x→a
f (a) (g(x) − g(a))
g(x). (f (x) − f (a))
+ lim
x→a
x−a
x−a
= lim g(x). lim
x→a
x→a
f (x) − f (a)
g(x) − g(a)
+ lim f (a). lim
x→a
x→a
x−a
x−a
= g(a)f 0 (a) + f (a)g 0 (a)
La dérivée du produit de deux fonctions est donné par :
(f (x).g(x))0 = f 0 (x).g(x) + f (x).g 0 (x)
On généraliser cette formule à un nombre quelconque de fonctions. On a :
(f (x).g(x).h(x))0 = f 0 (x).g(x).h(x) + f (x).g 0 (x).h(x)+
f (x).g(x).h0 (x)
(f1 (x).f2 (x)...fn (x))0 = f10 (x).f2 (x)...fn (x) + f1 (x).f20 (x)...fn (x)+
... + f1 (x).f2 (x)...fn0 (x)
0
Exemples ((x2 + 1)(x3 + x)) = (x2 +1)0 (x3 +x)+(x2 +1)(x3 +x)0 = 2x(x3 +x)+(x2 +1)(3x2 +
1) = 5x4 + 6x2 + 1
4.5.3
Dérivée d’un produit d’une fonction par une constante
On a :
(kf (x))0 = (k)0 f (x) + kf 0 (x) = kf 0 (x)
La dérivée du produit d’une fonction par une constante est donné par :
(kf (x))0 = kf 0 (x)
57
4.5. OPÉRATIONS SUR LES DÉRIVÉES
4.5.4
Dérivée d’un quotient de fonctions
On peut écrire
f (x) =
f (x)
.g(x)
g(x)
et, par dérivation des deux membres
0
f (x)
.g(x)
g(x)
f (x)
g(x)
f (x) =
⇔ f 0 (x) =
0
0
.g(x) +
f (x) 0
⇔ f 0 (x) −
.g (x) =
g(x)
f (x) 0
.g (x)
g(x)
f (x)
g(x)
0
.g(x)
f (x) 0
0
.g (x) f (x)
g(x)
=
g(x)
g(x)
f 0 (x) −
⇔
ou, en réduisant au même dénominateur :
0
f (x)
f 0 (x).g(x) − f (x).g 0 (x))
=
g(x)
g 2 (x)
La dérivée du quotient de deux fonctions est donné par :
f (x)
g(x)
0
=
f 0 (x).g(x) − f (x).g 0 (x))
g 2 (x)
0
x+1
1.(x2 + 3) − (x + 1)(2x)
(x + 1)0 (x2 + 3) − (x + 1)(x2 + 3)0
Exemples
=
=
=
x2 + 3
(x2 + 3)2
(x2 + 3)2
−x2 − 2x + 3
(x2 + 3)2
4.5.5
Cas particuliers
On a :
(f n (x))0 = (f (x).f (x)...f (x))0 = nf n−1 (x).f 0 (x)
en appliquant la formule du paragraphe 4.5.2.
De plus, on a :
1
f (x)
0
=
(1)0 .f (x) − 1.f 0 (x))
f 0 (x)
=
−
f 2 (x)
f 2 (x)
en appliquant la formule du paragraphe 4.5.4
58
CHAPITRE 4. LES DÉRIVÉES
4.6
4.6.1
Dérivée de la composée de deux fonctions
Introduction
Comparons les formules de dérivées obtenues ci-dessus :
• (f n (x))0 = nf n−1 (x).f 0 (x) et(xn )0 = nxn−1 (x)
0
0
1
1
(f 0 (x))
1
•
et
=− 2
=− 2
f (x)
f (x)
x
x
On constate que ces relations sont fortement similaires.
Dans ces relations, les premières de chaque série représente une fonction composée 1 (la composé
de f et de l’inverse d’une fonction, de f et d’une puissance de fonction).
4.6.2
Formule de dérivation
Soient deux fonctions f (g) et g(x) toutes les deux dérivables. On recherche la dérivée f 0 (g(x)).
D’après la définition de la dérivée, on peut écrire :
f 0 (x) = lim
∆x→0
ou encore
f 0 (x) = lim
∆x→0
f 0 (x) = lim
∆x→0
∆f
∆x
∆f ∆g
.
∆g ∆x
∆f
∆g
. lim
∆g ∆x→0 ∆x
ou, enfin :
f 0 (x) = lim
∆x→0
∆f 0
.g (x)
∆g
Puisque g(x) est dérivable, elle est continue. On a donc :
lim g(x) = g(a)
x→a
ou en reprenant les notations du paragraphe 4.2.3 et notant ∆g = g(x + ∆x) − g(x)
lim ∆g = 0
∆x→0
On peut donc écrire
f 0 (x) = lim
∆g→0
ou encore
∆f 0
.g (x)
∆g
f 0 (x) = f 0 (g).g 0 (x)
La dérivée d’une fonction composée est donc donnée par :
(f ◦ g(x))0 = (f (g(x))0 = f 0 (g(x)).g 0 (x)
1. voir pour rappel le paragraphe ?? du chapitre ??
59
4.7. DÉRIVÉES SUCCESSIVES
√
Exemple Considérons la fonction x√2 − 3x. On peut observer que cette fonction est la composée
de deux fonctions g(x) = x et f (x) = x2 − 3x. Dès lors :
√
4.7
x2 − 3x
0
2x − 3
1
(x2 − 3x)0 = √
= √
2 x2 − 3x
2 x2 − 3x
Dérivées successives
La dérivée d’une fonction étant elle-même une fonction, elle peut être dérivée.
Lorsque l’on dérive la dérivée d’une fonction, on trouve la dérivée seconde de la fonction de départ.
Il est évident que l’on peut continuer de la sorte indéfiniment et obtenir les dérivées troisième,
quatrième, cinquième,... d’une fonction donnée.
4.8
En résumé
(f (x) ± g(x))0 = f (x)0 ± g(x)0
(f (x).g(x))0 = f (x)0 g(x) + f (x)g(x)0
0
f (x)0 g(x) − f (x)g(x)0
f (x)
=
g(x)
g(x)2
(kf (x))0 = kf (x)0
(k)0 = 0
(x)0 = 1
(xn )0 = nxn−1
√ 0
1
( x) = √
2 x
0
1
1
=− 2
x
x
(f (x)n )0 = nf (x)n−1 f (x)0
p
0
f (x)0
f (x) = p
2 f (x)
0
1
f (x)0
=− 2
f (x)
f (x)
60
CHAPITRE 4. LES DÉRIVÉES
4.9
Exercices
1. En utilisant la définition du nombre dérivé, écrire l’équation de la tangente à la courbe
d’équation y = f (x) au point d’abscisse x = a si
√
x3
(a) f (x) = x et a = 2
(c) f (x) =
et a = 2
3
1
2
(b) f (x) = 1 + x + x et a = −
4
2. On donne la fonction f (x) = x2 + 2mx − 3 où m est un paramètre réel. Que vaut m si la
pente de la tangente à la fonction f (x) au point d’abscisse 2 vaut -1 ?
3. Dériver les fonctions suivantes (pour chaque étape, indiquer la formule utilisée) :
(a) f (x) = x3
1
(b) f (x) = 2
x
√
(c) f (x) = 3 x
1
(d) f (x) = √
2 x
(e) f (x) = 2x2 − x
(f) f (x) = x4 + 3x2 − 6
x2
(g) f (x) = 2ax3 −
+ c (a, b et c sont des
b
constantes)
√
√
3
(h) f (x) = 6 x7 + 4 x5 − 2x
4. Dériver les fonctions suivantes (pour chaque étape, indiquer la formule utilisée) :
√ 3
(a) f (x) = (1 + 4x3 )(1 + 2x2 )
(k) f (x) = (1 + 3 x)
q
p
(b) f (x) = x(2x − 1)(x2 − 6x + 3)
√
(l)
f
(x)
=
x+ x+ x
2
2x + 3x + 1
(c) f (x) =
1 − 4x
x(1 + x2 )
√
(m)
f
(x)
=
3
x +1
1 − x2
(d) f (x) = 2
p
x√− x − 2
(n) f (x) = 3 (4x − 1)2
x3
√
(e) f (x) =
(o) f (x) = 5x − x2 − 9
1 + x2
√
(f) f (x) = (2x2 + 3)2
x−1
3
(p) f (x) =
1
2x + 4
(g) f (x) = 1 −
√
x
1− x
√
√
(q) f (x) =
(h) f (x) = (x + 1) x − 1
1+ x
√
(x + 1)3
3
(i) f (x) =
1 + 3x
(r)
f
(x)
=
(2x
−
3)
2
rx
2x − 1
x+1
(s) f (x) = p
(j) f (x) =
(3x2 + 5x + 2)5
x−1
3x2 + 2mx + m
où m est un paramètre réel. Que doit valoir
x+m
m pour que la tangente à la courbe représentative de la fonction en son point d’intersection
avec l’axe des ordonnées soit parallèle à la droite d’équation d ≡ 2y + x − 3 = 0
5. On donne la fonction f (x) =
61
4.10. SOLUTIONS DES EXERCICES
4.10
Solutions des exercices
√
1. (a) y =
2. m = −
2
(x + 2)
4
8x + 15
16
4
(c) y = (3x − 4)
3
(b) y =
5
2
3. (a) 3x2
2
(b) − 3
x
1
(c) √
3
3 x2
1
(d) − √
4 x3
4. (a) 4x(10x3 + 3x + 1)
(b) 8x3 − 39x2 + 24x − 3
8x2 − 4x − 7
(c) −
(4x − 1)2
x2 − 4x + 1
(d)
(x − 2)2
√
x(3 − x2 )
(e)
2(x2 + 1)2
(f) 8x(2x2 + 3)
3(x − 1)2
(g)
x4
3x − 1
(h) √
2 x−1
(x − 2)(x + 1)2
(i)
3
r x
x+1
x−1
(j)
(x + 1)(x − 1)
√
( 3 x + 1)2
√
(k)
3
x2
2
5. m =
5
(e) 4x − 1
(f) 4x3 + 6x
2x
b
√
20 √
3
x2 − 2
(h) 21 x5 +
3
p√ √
√
√
(2 x + 1)
x( x + 1) + 4x( x + 1)
qp
(l)
√ √
√
8x( x + 1)
x( x + 1) + x
(g) 6ax2 −
2x4 − 3x2 − 1
(m) − p
(1 − x2 )3
8
√
3
3( 4x − 1
√
5 x2 − 9 − x
√
(o)
x2 − 9
(n)
(p)
4−x
√
4(x + 2)2 x − 1
1
(q) − √ √
x( x + 1)2
(r)
3(2x − 3)2 (14x + 1)
√
2 3x + 1
(s)
3(11 − 16x2 )
p
2 (3x2 + 5x + 2)7
62
CHAPITRE 4. LES DÉRIVÉES
Chapitre 5
Applications de la dérivée
5.1
5.1.1
Croissance et décroissance
Rappels : croissance, décroissance, minimum et maximum
Définition: Soit une fonction f (x) et un intervalle [a, b] du domaine de
définition.
Une fonction est croissante sur l’intervalle [a, b] si et seulement si ∀x1 , x2 ∈ [a, b] : x2 ≥ x1 ⇒ f (x2 ) ≥ f (x1 ).
Une fonction est décroissante sur l’intervalle [a, b] si et
seulement si ∀x1 , x2 ∈ [a, b] : x2 ≥ x1 ⇒ f (x2 ) ≤ f (x1 ). Une
fonction passe par un maximum sur l’intervalle [a, b] lorsqu’elle cesse de croître pour commencer à décroître.
Une fonction passe par un minimum sur l’intervalle [a, b]
lorsqu’elle cesse de décroître pour commencer à croître.
Remarque Un minimum (maximum) n’est pas nécessairement le point le plus bas (haut) de la
fonction. Il s’agit d’une notion "locale".
Figure 5.1 – Maximum et minimum, croissance et décroissance
63
64
CHAPITRE 5. APPLICATIONS DE LA DÉRIVÉE
5.1.2
par
Lien entre dérivée première et croissance
Choisissons donc deux valeurs x1 et x2 appartenant à l’intervalle [a, b] (x1 < x2 ). Définissons
• ∆x = x2 − x1
• ∆f = f (x2 ) − f (x1 )
Si la fonction f (x) est croissante, par définition ∆x et ∆f ont le même signe 1 ; le taux d’ac∆f
croissement
est donc positif. Quand la valeur de x2 se rapproche de celle de x1 , ce rapport
∆x
reste positif et devient la dérivée première f 0 (x) de la fonction.
Si la fonction f (x) est décroissante, par définition ∆x et ∆f sont de signes contraire ; le taux
∆f
est donc négatif. Quand la valeur de x2 se rapproche de celle de x1 , ce rapd’accroissement
∆x
port reste négatif et devient la dérivée f 0 (x) de la fonction.
Définition: Une fonction f (x) est croissante si sa dérivée première est
positive ; elle est décroissante si sa dérivée première est
négative.
5.1.3
Extremums
Les définitions des maximum et minimum (ou plus généralement "extremums") données au
paragraphe 5.1.1 montre que :
Définition: Une courbe représentative d’une fonction présente un extremum en un point si, en ce point, la dérivée première de
cette fonction s’annule et change de signe.
1. par lé définition du paragraphe 5.1.1
5.2. DÉRIVÉE SECONDE ET CONCAVITÉ
5.2
5.2.1
65
Dérivée seconde et concavité
Approche intuitive
Considérons le graphe d’une fonction f (x) donné ci-dessous.
On constate que le coefficient angulaire de la tangente à la courbe augmente 2 entre les points
A et C (où il est maximum). De même, il décroit entre C et E (où il est nul). Au delà de E, il
continue à décroître 3 jusqu’au point F (où il atteint une valeur minimale) pour réaugmenter de
nouveau jusqu’au point G (où il est à nouveau nul).
Le coefficient angulaire de la tangente à une courbe étant lié à la dérivée première de la
fonction et la qualité de croissance-décroissance d’une fonction étant lié au signe de cette dérivée
première, on peut dresser le tableau suivant :
x
coeff.angulaire
(f 0 (x))0 = f 00 (x)
xA
xB
xC
xD
xE
xF
xG
0 % % % M & & & 0 & m % 0
0 + + + + + + + 0 − − − 0
+ + + + 0 − − − − − 0 + +
On peut établir un lien entre le signe de la dérivée seconde et la concavité de la fonction.
5.2.2
Concavité et dérivée seconde
D’après l’exemple précédent (paragraphe 5.2.1), on peut conclure que :
Définition: Une fonction tourne sa concavité vers le haut si sa dérivée
seconde est positive. Elle tourne sa concavité vers le bas si
sa dérivée seconde est négative.
2. en valeur positive
3. en valeur négative
66
5.2.3
CHAPITRE 5. APPLICATIONS DE LA DÉRIVÉE
Point d’inflexion
Définition: Une courbe représentative d’une fonction admet un point
d’inflexion en I si et seulement si
• cette courbe admet une tangente en ce point
• la concavité de cette courbe change de sens en ce point
(c’est-à-dire que la dérivée seconde) s’annule et change
de signe).
5.3
Cas particuliers
Dans certains cas (principalement dans le cas des fonctions irrationnelles ou contenant des
valeurs absolues), une fonction peut être continue sans être dérivable (cf. paragraphe 4.2.4).
5.3.1
Point anguleux
Une fonction présente un point anguleux lorsque sa dérivée première est discontinue (c’està-dire qu’elle change de signe sans s’annuler).
p
Exemple La fonction f (x) = x2 (x + 1) présente un point anguleux en x = 0 comme le montre
le graphe suivant :
5.3.2
Point de rebroussement
Une fonction présente un point de rebroussement lorsqu’elle présente une tangente verticale
(sa dérivée première est infinie) et que sa dérivée première change de signe sans s’annuler.
Si la dérivée première ne change pas de signe mais est infinie, la fonction présente simplement
une tangente verticale.
p
Exemple La fonction f (x) = |x| présente un point de rebroussement en x = 0 comme le
montre le graphe suivant :
5.4. ETUDES DE FONCTIONS
5.4
5.4.1
67
Etudes de fonctions
Plan de travail
Nous adopterons le plan de travail suivant :
• Détermination du domaine de définition.
• Parité et périodicité.
• Etude de f(x).
– Zéros.
– Intersection avec l’axe des ordonnées (Oy).
– Signe.
• Recherche des équations des éventuelles asymptotes.
• Etude de f’(x).
– Zéros (qui permettent de déterminer les éventuels extremums).
– Signe (qui permet de déterminer la croissance et la décroissance).
• Etude de f”(x).
– Zéros (qui permettent de déterminer les éventuels points d’inflexion et les équations de
tangentes en ces points).
– Signe (qui permet de déterminer la concavité de la courbe).
• Détermination de quelques points particuliers.
• Tableau récapitulatif.
– 1re ligne : valeurs particulières de la variable par ordre croissant ;
– 2e ligne : les zéros, les pôles et le signe de f’(x) ;
– 3e ligne : les zéros, les pôles et le signe de f”(x)’ ;
– 4e ligne : croissance et décroissance de f(x) ;
– 5e ligne : concavité.
• Esquisse du graphique.
68
CHAPITRE 5. APPLICATIONS DE LA DÉRIVÉE
5.4.2
Premier exemple
Soit à étudier la fonction
−x3 − x2 + x + 1
x2
Les étapes de l’étude de fonction complète sont détaillées ci-après.
1. Domaine :
CE : x2 6= 0 ⇔ x 6= 0.
Le domaine est donc R0
f (x) =
2. Zéros :
⇔
⇔
⇔
⇔
f (x) = 0
−x3 − x2 + x + 1 = 0
−x2 (x + 1) + (x + 1) = 0
(1 − x2 )(x + 1) = 0
(1 − x)(x + 1)2 = 0
Les zéros sont donc x = 1 et x = −1 (qui sont tous les deux dans le domaine de définition
de la fonction).
3. Intersection avec l’axe 0y : f (0) n’existe pas car 0 est hors domaine.
−(−x)3 − (−x)2 + (−x) + 1
qui n’a rien à voir ni avec f (x) ni avec −f (x).
4. Parité : f (−x) =
(−x)2
La fonction n’est donc ni paire ni impaire.
5. Signe : Le signe est résumé dans le tableau de signe suivant :
x
1−x
(x + 1)2
x2
f (x)
−1
+
+
+
+
0
0
0
+
+
+
+
1
+ 0 −
+
+
0 +
+
±∞ + 0 −
6. Asymptotes
(a) Asymptote verticale : 0 est rejeté du domaine, on obtient
lim f (x) =
x→0
1
= +∞
0
d’après le tableau du point 5.
(b) Il n’y a pas d’asymptote horizontale car on est en présence d’une fonction rationnelle
et le degré du numérateur et supérieur au degré du dénominateur.
(c) Asymptote oblique : la division euclidienne de numérateur par le dénominateur donne
f (x) = −x − 1 +
x+1
x2
x+1
Lorsque x tend vers l’infini 4 , le troisième terme ( 2 tend vers zéro car le degré du
x
numérateur est inférieur à celui du dénominateur. Dès lors, on peut affirmer que si x
tend vers l’infini la fonction tend vers la fonction g(x) = −x − 1 qui se représente graphiquement par une droite. On est en présence de la définition d’une asymptote 5 .Dès
lors, la droite d’équation y = −x − 1 est asymptote oblique de la fonction f (x).
4. ce qui correspond à la situation d’une asymptote
5. "droite de laquelle un courbe se rapproche indéfiniment sans jamais la toucher "
69
5.4. ETUDES DE FONCTIONS
7. Dérivée première : On a successivement :
0
f (x) =
−x3 − x2 + x + 1
x2
0
=
(−x3 − x2 + x + 1)0 (x2 ) − (−x3 − x2 + x + 1)(x2 )0
x4
=
(−3x2 − 2x + 1)(x2 ) − (−x3 − x2 + x + 1)2x
x4
=
(−3x2 − 2x + 1)(x2 ) − (−x3 − x2 + x + 1)2x
x4
=x
(−3x2 − 2x + 1)(x) − (−x3 − x2 + x + 1)2
x4
=
−3x3 − 2x2 + x + 2x3 + 2x2 − 2x − 2
x3
=
−x3 − x − 2
x3
=
−(x + 1)(x2 − x + 2)
x3
Le tableau de signe de la dérivée première est détaillé ci-dessous
x
−(x + 1)
x2 − x + 2
x3
f 0 (x)
−1
0
+ 0 −
+
+
−
− 0
− 0 + ∞
−
+
+
−
Ce tableau est le tableau de variation de la fonction f (x).
8. Dérivée seconde : Lorsque que l’on redérive la fonction obtenue au point 7, on obtient :
f 00 (x) =
2(x + 3)
x4
Le tableau de signe de la dérivée seconde est :
x
−3
0
2(x + 3) − 0 +
+
4
x
+
+ 0 +
f 00 (x) − 0 + ∞ +
9. Tableau récapitulatif :
Le tableau récapitulatif du comportement de la fonction est présenté ci-dessous.
70
CHAPITRE 5. APPLICATIONS DE LA DÉRIVÉE
x
f (x)
f 00 (x)
−∞
0
−3
−
−
f (x)
+
&
∩
0
−
+
−1
0
+
+
0
∞
∞
1
−
+
+∞
−
+
+
0
+ A.V. + 0 −
P.I. &
m
%
& 0 &
−3, 16
∪
(−1,
0)
∪
∪
∪
9
A.O.
A.O.
Le graphe de la fonction est le suivant 6
6. Il doit être dessiné à l’aide de la calculatrice graphique avant de démarrer l’étude car tous les résultats
des calculs peuvent y être vérifiés ! !
71
5.4. ETUDES DE FONCTIONS
5.4.3
Deuxième exemple
Soit à étudier la fonction
f (x) =
√
x2 − 3x − 4 − 2x
Les étapes de l’étude de fonction complète sont détaillées ci-après.
1. Domaine :
CE : x2 − 3x − 4 ≥ 0 ⇔ (x + 1)(x − 4) ≥ 0
−1
4
x
x2 − 3x − 4 + 0 − 0 +
Le domaine est donc : −∞, −1] ∪ ]3, +∞
√
2. Zéros : f (x) = 0 ⇔ x2 − 3x − 4 − 2x = 0
√
√
x2 − 3x − 4 − 2x = 0 ⇔ x2 − 3x − 4 = 2x
⇔ x2 − 3x − 4 = 4x2
qui n’a pas de solution réelle.
3. Intersection avec l’axe 0y : f (0) n’existe pas car 0 est hors domaine.
4. Parité : Le domaine n’est pas symétrique par rapport à x = 0, la fonction n’est donc ni
paire ni impaire.
5. Signe 7 :
Si x ≤ −1 la fonction est toujours positive.
Si x ≥ 3, la fonction s’écrit :
√
f (x) = x2 − 3x − 4 − 2x
√
⇔ f (x) =
√
x2 − 3x − 4 − 2x
x2 − 3x − 4 + 2x
√
x2 − 3x − 4 + 2x
⇔
x2 − 3x − 4 − 4x2
f (x) = √
x2 − 3x − 4 + 2x
⇔
f (x) = √
−3x2 − 3x − 4
x2 − 3x − 4 + 2x
Le numérateur est toujours négatif (∆ < 0 et a < 0) et le dénominateur toujours positif
(x > 0), donc la fonction est toujours négative.
6. Asymptotes
(a) Asymptote verticale : il n’y a aucun point rejeté du domaine, donc il n’y a pas d’asymptote verticale.
(b) Asymptote horizontale : On a respectivement
lim f (x) = ∞ − ∞ F I
x→+∞
et
lim f (x) = +∞
x→−∞
7. L’étude de signe de telles fonctions est loin d’être immédiate et demande un certain "feeling"
72
CHAPITRE 5. APPLICATIONS DE LA DÉRIVÉE
On a donc une possibilité d’A.H. en +∞. Lorsqu’on lève l’indétermination :
lim f (x) = ∞ − ∞ F I
x→+∞
√
√
x2 − 3x − 4 − 2x
x2 − 3x − 4 + 2x
√
x2 − 3x − 4 + 2x
= lim
x→+∞
= lim
x→+∞
√
−3x2 − 3x − 4
x2 − 3x − 4 + 2x
+∞
F.I.
+∞
=
= lim
x→+∞
√
−3x2
x2 + 2x
= +∞
Il n’y donc pas d’asymptote horizontale.
(c) Asymptote oblique : On a :
∞
f (x)
=
FI
x→+∞
x
∞
√
√
x2 − 3x − 4 − 2x
x2 − 3x − 4 + 2x
√
= lim
x→+∞
x x2 − 3x − 4 + 2x
m = lim
= lim
x→+∞
−3x2 − 3x − 4
√
x x2 − 3x − 4 + 2x
+∞
F.I.
+∞
=
= lim
−3x2
√
x
x2 + 2x
= lim
−3x2
x (x + 2x)
x→+∞
x→+∞
= −1
et
p = lim (f (x) + x) = lim
x→+∞
x→+∞
√
x2 − 3x − 4 − x = ∞ − ∞ F.I.
3
En levant l’indétermination, on obtient : p = − .
2
3
On a donc une A.O. en +∞ d’équation y = −x − .
2
3
En effectuant le même calcul en −∞, on obtient une A.O. d’équation y = −3x +
2
73
5.4. ETUDES DE FONCTIONS
7. Dérivée première : Après calcul et simplification, on obtient :
√
4 x2 − 3x − 4 − 2x + 3
0
√
f (x) = −
2 x2 − 3x − 4
Le tableau de signe de la dérivée première est détaillé ci-dessous :
√
5 3 3
x
−1
4
+
3
2
0
f (x) − ±∞ //// ±∞ +
0
−
Ce tableau est le tableau de variation de la fonction f (x).
8. Dérivée seconde : Lorsque que l’on redérive la fonction obtenue au point 7, on obtient :
−25
f 00 (x) = q
4 (x2 − 3x − 4)3
Cette fonction est toujours négative
9. Tableau récapitulatif :
Le tableau récapitulatif du comportement de la fonction est présenté ci-dessous.
−1
x
4
f 0 (x)
f 00 (x)
− ±∞ //// ±∞ +
− ±∞ //// ±∞ −
f (x)
+
&
∩
A.O.
2
////
////
////
−8
√
5 3 3
+
3
2
0
−
−
−
−
% M
&
√
√
5 3
5 3
3
∩
+ 2, − 2 − 3
∩
3
A.O.
74
CHAPITRE 5. APPLICATIONS DE LA DÉRIVÉE
Le graphe de la fonction est le suivant 8
5.5
Problème d’extrémum
Les problèmes d’extrémums permettent d’"optimiser" une situation réelle selon des critères
bien définis. Le principe de résolution de ce genre de problème est d’exprimer la quantité variable
Q en fonction d’une (ou plusieurs) variable(s) et de déterminer les valeurs de la (ou les) variable(s)
pour lesquelles la quantité Q présente un extrémum (c’est-à-dire telles que Q0 = 0).
Un exemple va nous permettre de comprendre comment traiter les problèmes d’optimisation.
8. Il doit être dessiné à l’aide de la calculatrice graphique avant de démarrer l’étude car tous les résultats
des calculs peuvent y être vérifiés ! !
5.6. THÉORÈME DES VALEURS INTERMÉDIAIRES
75
Exemple Une usine fabrique des boîtes de conserve cylindriques. Sachant que le volume d’une
boîte doit être de 1 dm3 , déterminer ses dimensions (hauteur et rayon de la base) de
telle manière que la quantité de tôle utilisée soit minimum.
Le volume d’une boîte cylindrique est donné par V = πR2 h où R représente le rayon
de la base et h la hauteur.
Il faut que πR2 h = 1000 si nous exprimons le volume mesuré en cm3 .
1000
(car évidemment R 6= 0 ).
Cette expression permet d’écrire h =
πR2
L’aire latérale du cylindre s’obtient par la formule 2πRh, tandis que l’aire de chacune
des bases vaut πR2 . L’aire totale s’écrit donc 2πRh + 2πR2 . Cette expression doit
être minimum.
Compte tenu de la valeur de h obtenue plus haut, on obtient la fonction de R :
f (R) = 2πR
2000
1000
2
+ 2πR2
+
2πR
=
2
πR
R
Pour que cette fonction admette un extremum, il faut que sa dérivée première soit
nulle :
2000
f 0 (R) = − 2 + 4πR
R
qui s’annule pour :
r
3 1000
R=
2π
Il en résulte que la boîte doit avoir un rayon de base de 5,4 cm environ et une hauteur
de 10,9 cm.
5.6
Théorème des valeurs intermédiaires
Soit f : [a, b] → R une application continue, alors pour tout réel u compris entre f (a) et f (b),
il existe au moins un réel c compris entre a et b tel que f (c) = u.
Cas particulier :Théorème de Bolzano
Si f (x) est une fonction définie sur [a, b], dérivable et strictement monotone sur [a, b] et si, de
plus, f (a) et f (b) sont de signe contraire, il existe un et un seul réel c compris entre a et b tel que
f (c) = 0. Dès lors l’équation f (x) = 0 admet une seule solution dans l’intervalle ]a, b[.
Ces deux théorèmes sont admis sans démonstration et seront utilisés dans la méthode de
résolution numérique d’équation dite "méthode de dichotomie"(voir paragraphe 5.7
5.7
Résolution numérique d’équations
Soit f (x) une fonction continue. L’équation f (x) = 0 est parfois impossible à résoudre par
les méthodes algébriques. La notion de dérivée peut permettre d’obtenir de très bonnes approximations des racines de l’équation.
Pour résoudre f (x) = 0, il faut localiser et séparer les solutions, c’est-à-dire, pour chaque
solution x0 cherchée, trouver un intervalle ]a, b[ qui contient x0 et seulement cette valeur. Il faut
donc trouver un intervalle ]a, b[ où f (x) s’annule une seule fois.
76
CHAPITRE 5. APPLICATIONS DE LA DÉRIVÉE
Pour cela, on utilise le théorème de Bolzano (voir paragraphe 5.6).
Ainsi pour trouver un intervalle qui contient une et une seule solution x0 , il suffit de déterminer
a et b tels que
• f est définie sur [a, b] ;
• f 0 existe et garde un signe constant sur ]a, b[ ;
• f (a) et f (b) sont de signe contraire.
Il faut ensuite restreindre l’intervalle ]a, b[ pour augmenter la précision de x0 . Plusieurs techniques existent parmi lesquelles : la dichotomie et la méthode de Newton.
5.7.1
Méthode de dichotomie
Soit f (x) une fonction et ]a, b[ l’intervalle où une solution de l’équation f (x) = 0 a été
localisée. Supposons en outre que f (a) < 0 et f (b) > 0.
La méthode de dichotomie consiste à :
• trouver une valeur x1 de ]a, b[ ;
• calculer f (x1 ) ;
• si f (x1 ) > 0 alors x0 ∈]a, x1 [ ; si f (x1 ) < 0 alors x0 ∈]x1 , b[
On se retrouve donc en présence d’un intervalle dont les extrémités ont des images de signes
contraires et dont la taille a été diminuée. On procède de même avec une autre valeur x2 et ainsi
de suite jusqu’à l’obtention d’une précision donnée. Il s’agit ici d’une méthode "itérative".
Remarquons que si f (a) > 0 et f (b) < 0, la méthode reste la même mais le choix du nouvel
intervalle doit être adapté.
77
5.7. RÉSOLUTION NUMÉRIQUE D’ÉQUATIONS
Exemple Soit à trouver les racines de l’équation x3 − 3x + 1 = 0.
L’étude de la dérivée première montre que la fonction est croissante sur l’intervalle
−∞, −1[∪]1, +∞[ et décroissante ailleurs.
Considérons l’intervalle de départ ]0, 1[ où f (0) > 0 et f (1) < 0.
3
0+1
. On a f (x1 ) = − ≈ −0.375.
Prenons comme valeur x1 =
2
8 1
Comme f (x1 ) est négative, on travaille sur l’intervalle 0, .
2
1
0+
2 et on a f (x ) = 17 ≈ 0.265 et ainsi de suite.
On choisit alors une valeur x2 =
2
2
64
Le tableau suivant reprend les résultats des différents calculs suivants.
Etape
3
4
5
Intervalle
1 1
,
4 2
1 3
,
4 8
5 3
,
16 8
xi
3
8
5
16
11
32
f (xi )
37
−
≈ −0.072
152
381
≈ 0.093
4096
307
≈ 0.009
32768
On constate que, au bout de 5 étapes de calcul, la valeur de f (xi ) est proche de zéro.
11
On peut donc considérer avec relativement peu d’erreur la valeur
(0.34375) comme
32
le zéro de la fonction a .
a. En réalité, le vrai zéro compris dans l’intervalle de départ ]0, 1[ vaut ≈ 0.3472963
5.7.2
Méthode de Newton
La méthode de Newton 9 consiste à trouver la solution d’une équation f (x) = 0 en approximant la fonction en un point par sa tangente en ce point.
Pour cela, partant d’un point x0 que l’on choisit de préférence proche du zéro à trouver (en faisant
des estimations grossières par exemple), on approche la fonction par sa tangente en ce point. Une
nouvelle approximation du zéro de la fonction x1 sera le zéro de la tangente.
On recommence le calcul précédent jusqu’à avoir une approximation du zéro qui ne varie pas
d’une itération à l’autre.
9. Isaac Newton(4 janvier 1643 - 31 mars 1727) est un philosophe, mathématicien, physicien, alchimiste,
astronome et théologien anglais
78
CHAPITRE 5. APPLICATIONS DE LA DÉRIVÉE
L’équation d’une tangente à une courbe d’équation y = f (x)au point d’abscisse x0 est :
y − f (x0 ) = f 0 (x0 )(x − x0 )
Le zéro de cette tangente (x1 ) est tel que y = 0, ou :
x1 = x0 −
f (x0 )
f 0 (x0 )
Exemple Soit à trouver les racines de l’équation cos x = x3 .
La dérivée de la fonction
f (x) = cos x − x3
est
f 0 (x) = − sin x − 3x2
1
Partons de x0 = . Le tableau suivant reprend les différents stades des calculs.
2
Etape
xi
1
2
3
4
0.5
1.11214
0.90967
0.86626
f (xi )
f 0 (xi )
1.11214
0.90967
0.86626
0.86548
xi+1 = xi −
Ici aussi, la méthode converge rapidement vers une solution qui varie peu d’une itération à l’autre (0.001) a .
a. La vraie solution de cette équation est 0.8654740331
79
5.8. EXERCICES
5.8
Exercices
1. Trouver les extremums des fonctions suivantes et en étudier les variations :
(a) f (x) = x3 − 3x
x2 + 2
(b) f (x) = √
x−1
Déterminer les coordonnées de ces extremums.
x+2
2. Etudier les variations de la fonction f (x) = 2
et écrire l’équation de la tangente au
x −3
graphique de f (x) au point d’abscisse 2.
3. Calculer la valeur de a pour que la fonction f (x) = x2 + ax + 1 ait un minimum en x = 2.
4. On donne la fonction f (x) = x3 − 4ax + b où a et b sont des nombres réels. Déterminer a et
b pour que f (x) soit minimum en x = 1 et comprennent le point (1,-5).
x2 + mx + p
ait un minimum en x = 1 et
2(x + 1)
passe par le point (0,1). m et p sont des nombres réels.
5. Trouver m et p pour que le graphique de f (x) =
6. On donne les tableaux de variations suivants. Après avoir complété le tableau en ayant fait
apparaitre la variation et la concavité de la fonction, établir une ébauche de graphe pour
chaque fonction ainsi décrite.
x
−∞
−1
0
1
+∞
f 0 (x)
+
+ 1 +
+
(a) 00
−
− 0 +
+
f (x)
f (x) −∞
−2
0
2
+∞
1
x
−∞
−1
− 12
0
1 +∞
2
0
f (x)
− 0 + + + 0 − − − 0 +
(b) 00
f (x)
+ + + 0 − − − 0 + + +
f (x) +∞
2
2.5
3
2.5
2
+∞
x
−∞
f (x)
−
(c) 00
−
f (x)
f (x) −1
0
1
2
+∞
|
+ 0 − − −
|
− − − 0 +
0
− 21
−1
−∞ |−∞
x
−∞
f (x)
−
(d) 00
f (x)
−
f (x)
0
−1
0
|
− − −
|
+ 0 −
+∞
0
−∞ |
0
0
x
f 0 (x)
(e) f 00 (x)
f (x)
−∞
−
−
+∞
AO ≡ y = −x +
3
2
1
+∞
|
−
|
+
+∞
0
−∞ |
1
2
|
/////////////
|+∞ +
−∞
| ///////////// |
−
0 ///////////// 0
+∞
+∞
AO ≡ y = x −
3
2
80
CHAPITRE 5. APPLICATIONS DE LA DÉRIVÉE
x
−∞
f (x)
−
(f) 00
−
f (x)
f (x) +∞
0
0
2
+∞
+ + +
−∞ |
|
− 0 +
1
2
x
−∞
−2
f (x)
− − −
(g) 00
f (x)
− − −
f (x)
0
−1
0
−1
|
−
|
+
+∞
−∞ |
x
−∞
0
f (x)
− −1| + 1 +
(h) 00
f (x)
−
|
+
f (x)
1
0
0
3
|
|
4
+∞ +∞
0
+1
−1 |
|
1
+∞
+
−
+∞
+
+
+∞
|−∞
1
|
|
2 +∞
+ + +
− − −
−1
0
1
2
+∞
|
+ + +
|
− − −
+∞
|−∞
−2
1
7. Etudier complètement les fonctions suivantes
(a) f (x) = (x + 2)2 (x − 1)
x3
(b) f (x) = 2
x −1
√
(c) f (x) = |x + 2| 1 − x
√
(d) f (x) = x2 − 5x + 4
p
(e) f (x) = x(x − 2)2
ax2 + bx + c
et (C) sa courbe représentative
x−2
dans un plan muni d’un repère orthonormal. Déterminez a, b, c pour que (C) ait les propriétés
suivantes :
• (C) passe par le point A(0; 5)
• la tangente à (C) au point A est parallèle à l’axe des abscisses ;
• la tangente à (C) au point B d’abscisse 1 a pour coefficient directeur -3.
Etudier les variations de la fonction f ainsi obtenue.
8. Soit f la fonction définie sur R\{2} par f (x) =
5.8. EXERCICES
81
9. On donne les graphes des fonctions suivants. Pour chacun, établir le tableau récapitulatif
du comportement de la fonction.
(2x − 2)2
définie sur R\ 12 . On désigne par C sa courbe
2x − 1
représentative dans un repère orthogonal
10. On considère la fonction f (x) =
1
(a) Déterminer la limite de f (x) en . Quelle conséquence graphique en tire-t-on pour C ?
2
c
(b) Déterminer les réels a, b et c tels que f (x) = ax + b +
sur le domaine de
2x − 1
définition.
(c) En déduire le comportement de la fonction en +∞ et en −∞.
(d) En déduire que la droite d ≡ y = 2x − 3 est une asymptote oblique de C. Etudier la
position relative de d et C.
(e) Utiliser la forme trouvée en 10b pour calculer la dérivée f 0 (x) de f (x). Dresser le
tableau de variation de f (x).
(f) Ecrire l’équation de la tangente à C au point d’abscisse 2.
82
CHAPITRE 5. APPLICATIONS DE LA DÉRIVÉE
11. Soit la fonction f (x) =
2x2 − 7x + 11
x−2
(a) Calculer la limite de f (x) − (2x − 3) lorsque x tend vers +∞ et vers −∞. Conclure.
(b) Etudier la variation de f (x) et dresser son tableau de variation
(c) Donner une équation de la tangente au point d’abscisse 3.
(d) Donner les abscisses des points où la courbe admet une tangente horizontale.
(e) La courbe admet-elle une tangente parallèle à la droite d’équation d ≡ y − 2x = 0. Si
oui en quelle(s) abscisse(s) ?
x3
12. On donne la fonction f (x) =
et le graphe de sa dérivée f 0 (x).
2
(x − 1)
(a) Etablir l’équation des asymptotes de f (x).
(b) Sur base du graphe de f 0 (x) (et sans la calculer explicitment,), établir le tableau récapitulatif en le justifiant.
13. Soit la fonction f de R dans R définie par :
p
f (x) = 3 (x + 2)(x − 1)2
et C la courbe d’équation y = f (x)
(a) Calculer f 0 (x) et f 00 (x) et préciser les domaines de définition de f 0 (x) et f 00 (x).
(b) Déterminer une équation cartésienne
i. de la tangente à C au point d’abscisse -1
ii. des asymptotes (éventuelles) de C
(c) Établir le tableau récapitulatif du comportement de f .
5.8. EXERCICES
83
14. Quelles doivent être les dimensions d’un rectangle de périmètre 64 mètres pour que son aire
soit maximale.
15. Un fermier désire clôturer une superficie rectangulaire de 8000 m2 bordant une autoroute.
La clôture de long de l’autoroute lui coûte 10e par mètre alors que celle des autres côtés
coûte 7e par mètre. Trouver le coût minimal des travaux.
16. Une compagnie fabrique des boîtes avec des pièces de carton de 16cm par 10cm (en coupant
des carrés à chaque coin et en relevant les côtés). Quelles sont les dimensions de la boite de
volume maximal pouvant être obtenue ? Calculer ce volume maximal.
17. On donne un cercle de rayon r = 1. Parmi les triangles isocèles inscrits dans ce cercle, quels
sont ceux dont l’aire est maximale ? Dans ce cas que vaut l’angle au sommet ?
18. Considérons une tente en forme de cône circulaire droit, dont le rayon de base est R, et dont
la hauteur vaut h (on ne considère pas de tapis de sol). On impose un volume V de la tente.
h
faut-il choisir pour que l’aire du tissu utilisé soit minimale ? Calculer R et
Quel rapport
R
h dans le cas où V = 2 m3
84
CHAPITRE 5. APPLICATIONS DE LA DÉRIVÉE
Troisième partie
Géométrie
85
Chapitre 6
Calcul vectoriel dans l’espace
6.1
Définitions
Soient A et B deux points distincts de l’espace.
−→
Définition: Le vecteur AB est une entité géométrique caractérisée par :
• sa direction (celle de la droite AB) ;
• son sens (de A vers B) ;
• sa longueur (ou sa norme) définie par la
distance
de A
−→
−→
à B. La norme du vecteur AB est notéeAB = d(A, B)
Figure 6.1 – Définition d’un vecteur
Remarques • A est l’origine du vecteur et B est l’extrémité du vecteur.
−→ →
−
• le vecteur nul est le vecteur dont l’origine coïncide avec l’extrémité : AA = 0
• un vecteur peut également être représenté par une seule lettre (sans mentionner
−
explicitement l’origine et l’extrémité) : →
u
87
88
6.2
6.2.1
CHAPITRE 6. CALCUL VECTORIEL DANS L’ESPACE
Opérations sur les vecteurs
Vecteurs égaux
Définition: Deux vecteurs sont égaux s’ils ont le même sens, la même
direction et la même norme.
−→ −
−
Dans la figure de la page suivante, les vecteurs AB, →
u et →
v sont égaux.
Figure 6.2 – Egalité de vecteur
Propriétés Considérons quatre points A, A, C et D non alignés de l’espace.
−→ −−→
−−→ −−→
Si AB = DC et/ou AD = BC alors ABCD est un parallélogramme et réciproquement. La démonstration de cette propriété est laissée au soin du lecteur.
Cette propriété est très utile pour démontrer qu’un quadrilatère est un parallélogramme.
Remarque Il faut être très attentif à la manière de nommer les sommets d’un polygone. Deux
lettres consécutives dans le nom du polygone doivent être reliées par un segment.
6.2.2
Vecteurs opposés
Définition: Deux vecteurs sont opposés s’ils ont :
• même direction ;
• même longueur ;
• sens opposé.
−→
−→
On écrit alors : AB = −BA
89
6.2. OPÉRATIONS SUR LES VECTEURS
6.2.3
Somme de vecteurs
Vecteurs consécutifs
Définition: Deux vecteurs sont consécutifs si l’extrémité du premier
coïncident avec l’origine du second.
Dans ce cas, la somme de deux vecteurs est définie par :
−→ −−→ −→
AB + BC = AC
Cette relation est la loi de Chasles 1
Figure 6.3 – Relation de Chasles
Cette relation est fondamentale pour le calcul vectoriel. En effet, elle permet d’exprimer que
"la somme de deux vecteurs consécutifs est un vecteur dont l’origine est l’origine
du premier vecteur et l’extrémité, l’extrémité du second vecteur "
(lecture de la relation de gauche à droite) mais surtout que
"tout vecteur peut être décomposé en la somme de deux vecteurs consécutifs"
(lecture de la relation de droite à gauche).
1. Michel Chasles, né à Épernon (Eure-et-Loir) le 15 novembre 1793 et mort à Paris le 18 décembre 1880
90
CHAPITRE 6. CALCUL VECTORIEL DANS L’ESPACE
La relation de Chasles peut être généralisée à un nombre quelconque de vecteurs.
Figure 6.4 – Relation de Chasles généralisée
−→ −→ →
−
Remarquons que la somme de deux vecteurs opposés donne le vecteur nul (AB + BA = 0 )
Vecteurs quelconques
Si les vecteurs sont quelconques, il suffit d’utiliser la définition des vecteurs égaux donnée
−→ −−→
au paragraphe 6.2.1. En effet, pour effectuer la somme AB + CD, il suffit de créer un vecteur
−−→0 −−→
BD = CD. Dès lors :
−→ −−→ −→ −−→0 −−→0
AB + CD = AB + BD = AD
(par la relation de Chasles).
Figure 6.5 – Somme de deux vecteurs quelconques
−−→
−→
Remarque on aurait tout aussi bien pu créer un vecteur A0 C égale au vecteur AB pour effectuer
−
−
→
−
−
→
−→ −−→
−−→
cette somme. On aurait eu alors : AB + CD = A0 C + CD = A0 D
6.2. OPÉRATIONS SUR LES VECTEURS
91
Vecteurs de même origine
Dans le cas particulier où les vecteurs on la même origine, le principe développé au paragraphe
6.2.3 est toujours utilisable.
Figure 6.6 – Somme de deux vecteurs de même origine
−−→0 −→
−−→0 −→
−→ −→ −→ −−→0
AC
ou
un
vecteur
AB.
Dès
lors
AB+AC = AB+BB =
On
construit
un
vecteur
BB
=
CB
=
−−→0
−→ −→ −→ −−→0 −−→0
AB ou AB + AC = AC + CB = AB .
Dans les deux cas le résultat est le même : la somme de deux vecteurs de même origine est un
vecteur égale à la diagonale du parallélogramme ABB 0 C
6.2.4
Différence de deux vecteurs
Soustraire deux vecteurs revient à additionner au premier l’opposé du second. On a donc
−→ −−→
−→
−−→
−→ −−→
AB − CD = AB + (−CD) = AB + DC. L’opération différence revient donc au même qu’une
opération somme.
Figure 6.7 – Différence de deux vecteurs
92
CHAPITRE 6. CALCUL VECTORIEL DANS L’ESPACE
6.2.5
Produit d’un vecteur par un réel
−→
Considérons un vecteur AB et un nombre réel k (k ∈ R0 ).
−→
Définition: Le vecteur k.AB est un vecteur :
−→
• de même direction que AB ;
−→
• de même sens que
si k > 0 et de sens opposé si k < 0 ;
−→AB
• de longueur |k| AB .
−−→
−→ −→
1 −→
Dans la figure ci-dessous, CD = 2AB et EF = − AB
2
Figure 6.8 – Multiplication d’un vecteur par un réel
Pour construire le produit d’un vecteur par un réel, on utilise le théorème de Thalès 2 illustré
ci-dessous.
6.2.6
Propriétés des opérations sur les vecteurs
Les opérations décrites dans les paragraphes précédents donnent toute un vecteur comme
résultat.
−
−
−
On peut démontrer les propriétés suivantes concernant la somme vectorielle (∀→
u ,→
v ,→
w)
→
−
→
−
−
−
−
• le vecteur nul est neutre pour l’addition : →
u + 0 = 0 +→
u =→
u;
→
−
→
−
→
−
→
−
• la somme de deux vecteurs est commutative : u + v = v + u ;
−
−
−
−
−
−
−
−
−
• la somme vectorielle est distributive : →
u +→
v +→
w = (→
u +→
v)+→
w =→
u + (→
v +→
w ).
→
−
→
−
De même, pour la multiplication par un réel (∀ v , w , ∀a, b ∈ R0 )
−
−
−
• la somme de réel est distributive sur la multiplication par un réel : (a + b)→
u = a→
u + b→
u;
→
−
→
−
→
−
• la multiplication par un réel est distributive sur la somme vectorielle : a( u + v ) = a u +
−
a→
v ;
−
−
• (ab)→
u = a(b→
u ).
2. vu en 3ème
93
6.3. VECTEURS PARTICULIERS
6.3
6.3.1
Vecteurs particuliers
Vecteurs parallèles
Définition: Deux vecteurs sont parallèles s’ils ont la même direction.
Vectoriellement, le parallélisme s’exprime par :
−→ −−→
−→
−−→
AB//CD ⇔ ∃k ∈ R0 |AB = k.CD
Figure 6.9 – Vecteurs parallèles
6.3.2
Points colinéaires
Considérons trois points A, B et C de l’espace.
Définition: Les points A, B et C sont alignés si et seulement si :
−→
−→
∃k ∈ R0 |AB = k.AC
Figure 6.10 – Points alignés
Remarque Cette relation est vrai pour tous les vecteurs définis par A, B et C et ne doit être
démontrée que pour deux vecteurs choisis (elle est vrai pour le 3ème aussi).
94
CHAPITRE 6. CALCUL VECTORIEL DANS L’ESPACE
6.3.3
Combinaison linéaire de vecteurs
−
−
Définition: Un vecteur →
u est combinaison linéaire des vecteurs →
v et
→
−
w (en abrégé combili) si et seulement si :
−
−
−
∃a, b ∈ R0 |→
u = a.→
v + b.→
w
6.3.4
Points coplanaires
Considérons quatre points A, B, C et D de l’espace.
Définition: Les points A, B, C et D sont coplanaires si et seulement
si :
−→
−→
−−→
∃k1 , k2 ∈ R0 |AB = k1 .AC + k2 .AD
Remarque Cette relation est vrai pour tous les vecteurs définis par A, B, C et D et ne doit être
démontrée que pour deux vecteurs choisis (elle est vrai pour tous les autres aussi).
6.4
Base du plan
Pour placer un point dans l’espace on doit nécessairement se fixer trois axes non parallèles
et des unités de mesure sur chacun de ces axes. Pour représenter des vecteurs, on utilisera plutôt
−
→
− →
− →
desvecteurs
unités
( i , j , k )plutôt que des unités. Ces vecteurs sont tels que leur norme vaut
−
− →
− →
→
1 ( i = j = k = 1).
−
→
− →
− →
L’ensemble (O, i , j , k ) est appelé base de l’espace.
Dans le cadre de ce cours, on travaillera toujours en repère orthonormé (c’est-à-dire avec des axes
deux à deux perpendiculaires.
6.5
Expression d’un vecteur dans un repère orthonormé
Dans un repère orthonormé, considérons le point P (xP , yP , zP ) .xP , yP et zP sont les coor−
→
− →
− →
données du point P dans le repère (O, i , j , k ).
−−→ −−→
−→
−→
Le vecteur OP peut se décomposer en OP = OP 0 + P 0 P (par la loi de Chasles)ou encore
−→ −→ −−→0 −−0→
OP = OA + AP + P P .
−−→ −−→ −−→ −→
→
−
−→ −→ −−→ −→
→
−
→
−
Comme AP 0 = OB et P 0 P = OC, on peut écrire OP = OA+ OB + OC = xP i +yP j +zP k
(puisque les coordonnées d’un point représentent un multiple de l’unité de base).
→
−
−→
→
− →
−
Le vecteur OP peut donc être décomposé en fonction des vecteurs de base i , j et k .
−→
On dit que (xP , yP , zP ) sont les composantes du vecteur OP .
Remarquons que la décomposition d’un vecteur en fonction des vecteurs de base est unique
(à un point P correspond un et un seul triplet de coordonnées).
6.6. OPÉRATIONS SUR LES VECTEURS ET COMPOSANTES
95
Figure 6.11 – Composantes d’un vecteur
6.6
Opérations sur les vecteurs et composantes
−→ −−→
Dans la suite du paragraphe, on considérera les vecteurs OA et OB de composantes respec−→
−−→
tives OA : (xA , yA , zA ) et OB : (xB , yB , zB ). Toutes les opérations décrites dans le cours de 4ème
peuvent être généralisées sans peine.
6.6.1
Egalité de vecteurs
La décomposition d’un vecteur en fonction des vecteurs de base étant unique, l’égalité de
deux vecteurs entraînent l’égalité des composantes :

 x A = xB
−→ −−→
yA = yB
OA = OB ⇔

zA = zB
6.6.2
Somme de vecteurs
On a :
−→ −−→
OA + OB : (xA + xB , yA + yB , zA + zB )
Les composantes de la somme de deux vecteurs sont la somme des composantes de chacun des
vecteurs.
96
CHAPITRE 6. CALCUL VECTORIEL DANS L’ESPACE
6.6.3
Produit d’un vecteur par un réel
On a :
−−→
−→
−−→
OB = k.OA ⇔ OB : (k.xA , k.yA , k.zA )
Les composantes du produit d’un vecteur par un réel k sont le produit des composantes de ce
vecteur par le réel k.
6.6.4
Vecteurs opposés
−→
−→
L’opposé d’un vecteur est égal au produit de ce vecteur par −1 : −OA = −1.OA. Dès lors :
−→
OA : (−xA , −yA , −zA )
Les composantes de l’opposé d’un vecteur sont l’opposé des composantes du vecteur.
6.6.5
Composantes d’un vecteur quelconque
−→
Considérons un vecteur quelconque AB.
D’après la loi de Chasles, ce vecteur peut être décomposé en la somme de deux vecteurs consécutifs.
−→ −→ −−→
−→ −−→ −−→ −→
On a : AB = AO + OB = −OA + OB = OB − OA.
−→
Dès lors, les composantes de AB sont données par :
−→
AB : (xB − xA , yB − yA , zB − zA )
Les composantes d’un vecteur quelconque sont obtenues en effectuant la différence des coordonnées de l’extrémité et de l’origine.
97
6.6. OPÉRATIONS SUR LES VECTEURS ET COMPOSANTES
Application coordonnées du milieu d’un segment
−−→ 1 −→
On a AM = AB.
2
En terme de composantes, si le point M : (xM , yM ), on a :
1
(xM − xA , yM − yA , zM − zA ) = (xB − xA , yB − yA , zB − zA )
2

xB − x A


x M − xA =


2

yB − yA
En égalant les composantes :
yM − yA =

2


z − zA

 zM − zA = B
2

x B + xA

xM =


2

yB + yA
ou
yM =

2


 z = zB + zA
M
2
Dès lors, les coordonnées du milieu M du segment [AB] sont :
M:
xA + xB yA + yB zA + zB
,
,
2
2
2
Les coordonnées du milieu d’un segment correspondent à la moyenne arithmétique
des coordonnées des extrémités de ce segment.
Figure 6.12 – Milieu d’un segment
98
CHAPITRE 6. CALCUL VECTORIEL DANS L’ESPACE
6.7
6.7.1
Produit scalaire
Définition
→
−
−
Considérons deux vecteurs de même origine →
a et b et faisant un angle α entre eux.
−
Définition: Si kak représente la norme du vecteur →
a a , le produit sca→
−
−
laire des vecteurs →
a et b est :
→
→
−
− →
−
→
−
a . b = k a k . b . cos α
(6.7.1)
−
a. c’est-à-dire la longueur du vecteur →
a
Le produit scalaire de deux vecteurs est, contrairement aux autres opérations sur les vecteurs
vues au chapitre précédent, un nombre réel 3 .
Remarque Si l’un des vecteurs est le vecteur nul, le produit scalaire est nul.
6.7.2
Cas particuliers
Vecteurs alignés
Dans le cas de vecteurs alignés, l’angle entre les vecteurs vaut 0 et le produit scalaire des
→
−
−
vecteurs →
a et b vaut :
→
→
−
− →
−
−
a . b = k→
a k . b .cos0
→
→
−
− →
−
−
a . b = k→
a k. b Remarque :
norme d’un vecteur
Du cas particulier précédent il découle que
2
→
−
−
−
−
−
a .→
a = k→
a k . k→
a k = k→
ak
(6.7.2)
Vecteurs opposés
Dans le cas de vecteurs opposés, l’angle entre les vecteurs vaut π et le produit scalaire des
→
−
−
vecteurs →
a et b vaut :
→
→
−
− →
−
→
−
a . b = k a k . b . cos π
→
→
−
− →
−
→
−
a . b = −k a k. b 3. Les normes et le cosinus d’un angle sont en effet des nombres réels
99
6.7. PRODUIT SCALAIRE
6.7.3
Produit scalaire de deux vecteurs perpendiculaires
→
−
−
Lorsque les vecteurs →
a et b , l’angle entre les deux vecteurs vaut
vaut
→
→
−
π
− →
−
→
−
a . b = k a k . b . cos
2
→
−
→
−
a.b =0
π
2
et le produit scalaire
Conséquences • Le produit scalaire de deux vecteurs perpendiculaires est nul.
• Si le produit scalaire de deux vecteurs est nul, alors, les deux vecteurs sont
perpendiculaires ou un des deux vecteurs est le vecteur nul.
6.7.4
Produit scalaire dans un repère orthonormé
→
−
−
Soient deux vecteurs →
a et b placés dans un repère orthonormé. Ces deux vecteurs peuvent
être décomposés en fonction des vecteurs de base 4 . On a respectivement :
(
→
−
→
−
→
−
→
−
a = xa . i + ya . j + za . k
→
−
→
−
→
−
→
−
b = xb . i + yb . j + zb . k
Si l’on effectue le produit scalaire des deux vecteurs, on a respectivement
→
−
→
−
→
−
→
−
→
−
→
−
→
−
→
−
a . b = (xa . i + ya . j + za . k ).(xb . i + yb . j + zb . k )
−
→
−
→
−
→
−
→
−
→
−
→
−
→
−
→
− →
→
−
→
−
→
−
→
−
→
−
→
−
→
−
= xa . i .xb . i +xa . i .yb . j +xa . i zb . k +ya . j .xb . i +ya . j .yb . j +ya . j .zb . k +za . k .xb . i +za . k .yb . j +za
Par définition d’un repère orthonormé, on a
−
→
− →
→
− →
−
→
− →
−
i . j = 0, i . k = 0, k . j = 0
et
→
→
− →
−
− 2
i.i =i =1
Dès lors :
→
−
→
−
a . b = xa .xb + ya .yb + za .zb
(6.7.3)
Le produit scalaire de deux vecteurs en repère orthonormé est donc égal à la somme du produit
des composantes de ces vecteurs.
6.7.5
Applications
Norme d’un vecteur
D’après les relations (6.7.2) et (6.7.3), il vient successivement :
2
→
−
−
−
a .→
a = k→
a k = xa .xa + ya .ya + za .za = x2a + ya2 + za2
Dès lors
4. voir le paragraphe 6.5
p
−
k→
a k = x2a + ya2 + za2
100
CHAPITRE 6. CALCUL VECTORIEL DANS L’ESPACE
Angle entre deux vecteurs
D’après les relations (6.7.1) et (6.7.3), il vient successivement, en tenant compte de la relation
développée au paragraphe 6.7.5 :
→
→
−
− →
−
−
a . b = k→
a k . b . cos α
⇔ cos α =
xa .xb + ya .yb + za .zb
→
− −
k→
a k. b En tenant compte de la relation (6.7.3), on obtient :
→
−
→
−
a.b
p
⇔ cos α = p
x2a + ya2 + za2 . x2b + yb2 + zb2
6.8. EXERCICES
6.8
101
Exercices
1. On considère le volume suivant constitué de trois parallélépipèdes rectangle (|AF | = 3,
|F E| = 4 et |AG| = 2). De plus, les points M , N , O et P sont les milieux respectifs des
segments [GH], [HI], [KJ] et [LK]
(a) Déterminer deux vecteurs égaux aux vecteurs
−→
i. T R
−−→
ii. HE
(b) Déterminer un représentant des vecteurs suivants
−−→ −→
i. KE + DI
1 −−→ −−→
ii. DF − N Q
2
−−→ −→
iii. F B − OS
−→ −−→ −−→
iv. GF − ED + P N
−→
−−→
(c) Si l’on place l’origine des axes en F , l’axe Ox selon F A, l’axe Oy selon F D et l’axe
−→
Oz selon F L, déterminer les coordonnées des points B, I et S
−−→ −→ −→ −−→
−−→ −−→ −−→
2. Démontrer que si 2AX = AB + AC + AD alors 2BX = BC + AD
3. Dans un repère orthonormé Oxyz, déterminer les valeurs de a, b et c pour que
−→ −−→
(a) AB = CD si A(−2, 3, 1 − 2c), B(a − 1, 2, −1), C(1, 3b + 2, 0) et D(2a + 3, b, −3c)
(b) M (1, −2, 3) est le milieu de [AB] si A(a + 2c, 2b − 3, c − 2)) et B(3a − 1, b + 2, c + 2)
(c) G(2, 0, −c+1) est le centre de gravité du triangle ABC si A(2a, b+1, 2c), B(−3, b−2, 1)
et C(3a + 2, −2, 3c + 2)
4. Soit dans un repère les points A(1,-2,3), B(0,-1,1), C(-1,1,2) et D(3,-1,4).
(a) Placer les points dans un repère orthonormé ;
102
CHAPITRE 6. CALCUL VECTORIEL DANS L’ESPACE
−→ −−→ 3 −−→ −→ 5 −−→
(b) Déterminer les composantes de 2AB, 3BC + AD et CA − BD ;
2
3
−−→ −−→ 1 −−→
−−→
(c) Déterminer les coordonnées du point E tels que EC = BC − AD + 3DB ;
2
(d) Déterminer les coordonnées du points F tels que ADF E soit un parallélogramme.
5. Déterminer x pour que les points A, B, C et D soient coplanaires.
(a) A(−1, 0, 1), B(2, −1, 1), C(0, 1, 2) et D(9, x, 0)
(b) A(1, 3, −2), B(x, −1, 1), C(2, 1, 0) et D(3x, −9, 8)
6. Déterminer λ et µ pour que les vecteurs ~u et ~v soient colinéaires
(a) ~u = ~i + 2~j + 3~k et ~v = λ~i + µ~j − 2~k
(b) ~u = 2~i + 3~j − ~k et ~v = λ~i + (λ − 1)~j + µ~k
7. L’espace étant munis d’un repère othonormé, considérons les points A(1, 0, 1), B(2, 1, 0) et
C(0, 2, 2).
(a) Déterminer les coordonnées du centre de gravité G du triangle ABC ;
(b) Déterminer les coordonnées du centre de gravité K du tétraèdre OABC 5 ;
−−→ 3 −→
(c) Vérifier que OK = OG
4
8. On donne un cube M N P QM 0 N 0 P 0 Q0 . Son arête mesure 5cm.
−−−→ −−→ −−→ −−→
(a) Calculer les produits scalaires P 0 N 0 .M Q et N 0 N .P 0 M ;
−−→ −−→ −−−→ −→
(b) Calculer l’angle entre les vecteurs QM et QN , M 0 P 0 et QP ;
ˆ 0P
(c) Calculer la valeur de l’angle QM
9. Dans l’espace muni d’un
déterminer les réels a et b pour que les vecteurs
repère orthonormé,
−→
−→
−→
3 2b
AB : (1, 2, a) et AC : b − 2, − ,
soient orthogonaux au vecteur EF : (1, −2, 3)
4 3
10. Dans un repère orthonormé, on considère un cube M N P QM 0 N 0 P 0 Q0 dont l’arête a une
longueur 2.
−−→
−−→
−−→
(a) Démontrez que QN 0 est orthogonal à M P et à Q0 P
(b) Montrez que le triangle Q0 M P est équilatéral (en utilisant le produit scalaire)
5. Le centre de gravité d’un tétraèdre est l’intersection des médianes d’un tétraèdre, c’est à dire les droites
joignant un des sommets du tétraèdre et le centre de gravité de la face opposée
Quatrième partie
Trigonométrie
103
Chapitre 7
Rappel de trigonométrie
7.1
Nombres trigonométriques d’un angle dans un triangle
rectangle
Dans un triangle rectangle ABC on définit les nombres trigonométriques d’un angle
comme des rapport de longueurs de côtés de ce triangle.
Figure 7.1 – Trigonométrie dans le triangle rectangle
On définit ainsi 1 :
• le sinus d’un angle comme le rapport de la longueur du côté opposé à l’angle à la
AB
c
longueur de l’hypoténuse : sin C =
= ;
BC
a
• le cosinus d’un angle comme le rapport de la longueur du côté adjacent à l’angle à la
AC
b
= ;
longueur de l’hypoténuse : cos C =
BC
a
• la tangente d’un angle comme le rapport de la longueur du côté opposé à l’angle à la
AB
c
longueur du côté adjacent à l’angle : tan C =
= ;
AC
b
1. On se souviendra du moyen mnémotechnique "SOHCAHTOA"
105
106
CHAPITRE 7. RAPPEL DE TRIGONOMÉTRIE
7.2
Le cercle trigonométrique
Le cercle trigonométrique est un cercle :
• de centre O 2 ;
• de rayon 1 ;
• orienté positivement dans le sens contraire des aiguilles d’une montre.
Dans le cercle trigonométrique, des angles orientés seront représentés. Pour rappel, pour
définir un angle orienté, il faut :
• un sommet(O) ;
• une demi-droite origine([OI) ;
• une demi-droite extrémité([OA).
A tout angle orienté correspond un et un seul point image (A). Par contre un point du cercle
trigonométrique correspond à une infinité d’angles (donné à 2π près). Tout angle représenté par
un point du cercle trigonométrique se note sous la forme
α + 2kπ où k ∈ Z
La valeur de l’angle α comprise dans l’intervalle ] − π, π] est appelée valeur principale de l’angle.
Figure 7.2 – Le cercle trigonométrique
Ce cercle est divisé en quatre quadrants correspondant à des angles particuliers (0,
3π
).
2
2. l’origine du repère
π
, π,
2
7.2. LE CERCLE TRIGONOMÉTRIQUE
107
Figure 7.3 – Quadrants du cercle trigonométrique
Ce cercle permet de lire facilement les nombres trigonométriques de n’importe quel angle
orienté, comme le montre les figures suivantes.
Figure 7.4 – Lecture du cosinus et du sinus d’un angle orienté
108
CHAPITRE 7. RAPPEL DE TRIGONOMÉTRIE
Figure 7.5 – Lecture de la tangente et de la cotangente d’un angle orienté
Enfin, vu la présence d’axes orientés, les nombres trigonométriques d’un angle orienté ont des
signes dépendant du quadrant dans lequel l’angle se trouve. La figure suivante résume les signes
des différents nombres trigonométriques en fonction du quadrant.
Figure 7.6 – Signe des nombres trigonométriques
7.3
Identités fondamentales
Le triangle rectangle de la figure 7.1 permet de déduire les identités fondamentales suivantes
entre les nombres trigonométriques d’angles orientés :
sin2 a + cos2 a = 1
1
1 + tan2 a =
cos2 a
1
1 + cot2 a =
sin2 a
109
7.4. ANGLES REMARQUABLES
7.4
Angles remarquables
Il existe une série d’angles pour lesquels on peut trouver une valeur exacte des nombres
π
π π
trigonométriques. Il s’agit des angles , et .
6 4
3
L’ensemble des valeurs exactes des nombres trigonométriques des angles remarquables est résumé
dans le tableau suivant.
α
0
sin α
0
cos α
1
tan α
0
cot α
∞
π
6
1
2
√
3
2
√
3
3
√
3
π
4
π
2
π
3π
2
√
3
2
1
0
-1
1
2
0
-1
0
1
√
3
∞
0
∞
1
√
3
3
0
∞
0
√
2
2
√
2
2
π
3
Table 7.1 – Valeurs des nombres trigonométriques d’angles remarquables
7.5
Angles associés
Les angles associés permettent d’exprimer les nombres trigonométriques d’angles quelconques
(n’appartenant pas nécessairement au premier quadrant) en fonction d’angles se trouvant dans le
premier quadrant.
On retrouve aisément, à l’aide du cercle trigonométrique, les identités suivantes.
Angles supplémentaires
Angles anti-supplémentaires
sin(π − α) = sin α
cos(π − α) = − cos α
tan(π − α) = − tan α
cot(π − α) = − cot α
sin(π + α) = − sin α
cos(π + α) = − cos α
tan(π + α) = tan α
cot(π + α) = cot α
Angles opposés
Angles complémentaires
sin(−α) = − sin α
cos(−α) = cos α
tan(−α) = − tan α
cot(−α) = − cot α
sin
cos
tan
cot
π
− α = cos α
2
π
− α = sin α
2
π
− α = cot α
2
π
−
α = tan α
2
Table 7.2 – Angles associés
110
7.6
CHAPITRE 7. RAPPEL DE TRIGONOMÉTRIE
Exercices
iπ h
3
1. Sachant que cos x = − et que x ∈
, π , déterminer une valeur exacte de sin x et de
7
2
cot x.
√
7
3π
2. Sachant que tan x =
et que x ∈ π,
, déterminer une valeur exacte de sin x.
4
2
3. Dans un cercle trigonométrique de 5cm de rayon,
(a) placer le(s) angle(s) α dont le sinus vaut 0,3
(b) placer le point P représentant l’angle -156◦ et lire sur le cercle, une valeur approchée
de cos(−156◦ ) et tan(−156◦ )
(c) placer le(s) angle(s) β dont la cotangente vaut -1,2 et dont le cosinus est positif
4. Simplifier les expressions suivantes
π
(a) tan(x + 3π) + cot x + tan x −
2
3π
5π
(b) 3 tan x +
+ 2 tan x −
− 3 cot(x + π)
2
2
π
π
sin
− x sin(π + x)
sin(9π − x) tan x −
2
2
π
(c)
+
3π
cos
+ x cos(π − x) cot(x + 5π) cos
−x
2
2
3π
π
sin
− x cos x −
cot(x − 2π)
2
2
(d)
tan(3π + x) cot(−x) cos(π + x)
5. Simplifier l’expression suivante
3π
cos x +
2
cos(3π + x) tan(−x)
π
E(x) =
cot(7π + x) cos − − x
2
7π
−5π
Après simplification, calculer une valeur exacte de E
et de E
6
4
p
√
π
11π
10 + 2 5
=
, déterminer une valeur exacte de cos
et de
6. Sachant que cos
10
4
10
14π
sin
.
10
1
1
7. Remarques : on définit la sécante sec x =
et la cosécante csc x =
.
cos x
sin x
Démontrer les identités suivantes :
(a) tan x sin x = sec x − cos x
sin x
1 + cos x
(b)
+
= 2 csc x
1 + cos x
sin x
1
1
(c)
+
= 2 + 2 cot2 x
1 + cos x 1 − cos x
1 + sin x
(d) (tan x + sec x)2 =
1 − sin x
7.6. EXERCICES
sin2 a + sin a cos a + cos2 a
= 1 + tan a + tan2 a
cos2 a
sin3 a + cos3 a sin3 a − cos3 a
+
=2
(f)
sin a + cos a
sin a − cos a
sin2 a − cos2 b
(g)
= 1 − cot2 a cot2 b
sin2 a sin2 b
(e)
111
112
CHAPITRE 7. RAPPEL DE TRIGONOMÉTRIE
Chapitre 8
Formules de transformation
8.1
8.1.1
Formules d’addition
Introduction
Il est tentant d’écrire
cos (a + b) = cos a + cos b
Et cependant, l’exemple suivant montre le contraire
cos (60◦ + 30◦ ) = cos 60◦ + cos 30◦
ou
cos 90◦ = cos 60◦ + cos 30◦
ou encore
√
3
1
0 6= +
2
2
Ce paragraphe va établir les formules permettant de calculer les nombres trigonométriques 1 de
la somme et la différence de deux angles.
8.1.2
Formules des cosinus
Cosinus de la différence de deux angles
Considérons, sur la figure de la page suivante, une portion de cercle trigonométrique.
Sur ce cercle sont placés les points :
• A, représentatif de l’angle a et dont les coordonnées sont (cos a; sin a)
• B, représentatif de l’angle b et dont les coordonnées sont (cos b; sin b)
• C, représentatif de l’angle a − b et dont les coordonnées sont (cos(a − b); sin(a − b))
1. Nous nous limiterons dans le cadre de ce cours à sinus, cosinus et tangente
113
114
CHAPITRE 8. FORMULES DE TRANSFORMATION
Les triangles AOB et COI sont semblables 2 . On peut donc affirmer que
AB = CI ⇔ AB 2 = CI 2
En calculant la distance sur base des coordonnées, on a :
(cos a − cos b)2 + (sin a − sin b)2 = (cos(a − b) − 1)2 + (sin(a − b) − 0)2
ou, en développant les produits remarquables et en tenant compte de l’identité fondamentale de
la trigonométrie 3 :
2 − 2 cos a cos b − 2 sin a sin b = 2 − 2 cos(a − b)
En réorganisant les termes, on a :
cos(a − b) = cos a cos b + sin a sin b
Cosinus de la somme de deux angles
On a successivement :
cos(a + b) = cos [a − (−b)]
= cos a cos(−b) + sin a sin(−b)
Les relations entre les angles associés (voir paragraphe 7.5) permettent d’écrire :
cos(a + b) = cos a cos b − sin a sin b
2. deux côtés de même longueur encadrant un angle au sommet
3. cos2 x + sin2 x = 1
115
8.2. FORMULES DE DUPLICATION
8.1.3
Formules des sinus
En remarquant que 4 :
sin x = cos
On a
π
2
−x
hπ
i
− (a + b)
h2 π
i
= cos
− a − b)
π
π2 − a cos b + sin
− a sin b
= cos
2
2
sin(a + b) = cos
En réutilisant les angles associés, on obtient
sin(a + b) = sin a cos b + sin b cos a
De même, on démontre que :
sin(a − b) = sin a cos b − sin b cos a
8.1.4
Formules des tangentes
On a :
tan(a + b) =
sin(a + b)
cos(a + b)
En appliquant les formules développées aux paragraphes 8.1.2 et 8.1.3 et en divisant le numérateur
et le dénominateur de la fraction ci-dessus par le produit cos a cos b, on obtient :
tan(a + b) =
tan a + tan b
1 − tan a tan b
tan(a − b) =
tan a − tan b
1 + tan a tan b
De même :
8.2
8.2.1
Formules de duplication
Introduction
Les formules de duplication permettent de déterminer les nombres trigonométriques de l’angle
double. En effet, on ne peut écrire :
cos(2x) = 2 cos x
√
1
Pour s’en convaincre, il suffit de remarquer que cos 60◦ = 6= 2 cos 30◦ = 3.
2
Ce paragraphe va permettre d’établir les formules de duplication
4. voir paragraphe 7.5
116
CHAPITRE 8. FORMULES DE TRANSFORMATION
8.2.2
Formules du cosinus
On a
cos 2a = cos(a + a)
En appliquant les formules d’addition, on a :
cos 2a = cos a cos a − sin a sin a
ou encore
cos 2a = cos2 a − sin2 a
La relation fondamentale de la trigonométrie permet également d’écrire 5 :
cos 2a = 2 cos2 a − 1
(8.2.1)
cos 2a = 1 − 2 sin2 a
(8.2.2)
ou
8.2.3
Formule des sinus et des tangentes
De même, on montre que :
sin 2a = 2 sin a cos a
et
tan 2a =
8.3
2 tan a
1 − tan2 a
Formules de Carnot
Ces formules permettent de linéariser des expressions trigonométriques. Elles sont basée sur
les relations 8.2.1 et 8.2.2.
On peut écrire :
1 + cos 2a
cos2 a =
2
et
1 − cos 2a
sin2 a =
2
Ces relations sont les formules de Carnot.
8.4
Formules de Simpson
Les formules de Simpson 6 permettent de factoriser des expressions trigonométriques. Elles
sont basées sur les formules d’addition.
On a
sin(a + b) = sin a cos b + sin b cos a
et
sin(a − b) = sin a cos b − sin b cos a
5. en substituant sin2 a par 1 − cos2 a
6. Thomas Simpson (1710-1761), mathématicien britannique.
117
8.4. FORMULES DE SIMPSON
Faisons la somme de ces deux expressions. On obtient :
sin(a + b) + sin(a − b) = 2 sin a cos b
p+q
p−q
Posons p = a + b et q = a − b. On a également a =
et b =
.
2
2
On peut dès lors écrire :
p+q
p−q
sin p + sin q = 2 sin
cos
2
2
On démontre de même que
sin p − sin q = 2 cos
p−q
p+q
sin
2
2
p+q
p−q
cos
2
2
p−q
p+q
sin
cos p − cos q = −2 sin
2
2
7
Ces formules sont les formules de Simpson
cos p + cos q = 2 cos
7. Elles peuvent être retenue à l’aide du moyen mnémotechnique : "Si, coco, si ; coco, si si ! Priorité au sinus
et à l’addition, -2 à la dernière".
118
8.5
CHAPITRE 8. FORMULES DE TRANSFORMATION
Exercices
1. A l’aide des formules d’addition, montrez que
π
+ x = − sin x
(a) cos
2
π
√2
(b) sin
−x =
(cos x − sin x)
4
2
√
π
π
√3 + 1
3−1
(c) sin
+ x + cos
+x =
cos x +
sin x
6
6
2
2
2. Calculer après décomposition des angles en la somme ou la différence de deux autres angles
(remarquables).
5π
12
π
(b) tan
12
(c) sin105◦
(a) cos
3. Montrer que les expressions suivantes sont indépendantes de x :
2π
4π
+ x + sin
+x
(a) sin x + sin
3
3
(b) cos2 x − 2 cos a cos x cos(a + x) + cos2 (a + x)

√
iπ h

2

 sin a =
et a ∈
,π
2√
2
4. Calculer cos(a − b) et tan(a + b) si
3
3π


et b ∈ π,
 cos b = −
2
2
5. Montrer que
(a) cos a sin(b − c) + cos b sin(c − a) + cos c sin(a − b) = 0
(b) (1 − cos b cos c)2 − sin2 b sin2 c = (cos b − cos c)2
et résoudre l’équation x2 sin2 b − 2(1 − cos b cos c)x + sin2 c = 0
6. Etablir la relation permettant de calculer tan(a + b + c) et déduire la relation liant tan a,
tan b et tan c lorsque a, b et c sont les angles d’un triangle.
7. Vérifier et donner les conditions d’existence des identités suivantes
π
π
(a) cos4 a − sin4 a = cos 2a
(f) tan
+ a − tan
− a = 2 tan 2a
4
4
2
(b) tan a + cot a =
2
sin 2a
(g) sin 2a =
cot a − 1
1 − sin 2a
tan a + cot a
(c)
=
cot a + 1
cos 2a
sin 2a
cos a
a
(h)
.
= tan
(d) cos 2a(1 + tan a tan 2a) = 1
1 + cos 2a 1 + cos a
2
1 + cot2 a
1
=
(e)
(i) 4(cos6 a − sin6 a) = cos 2a(4 − sin2 2a)
2 cos a
sin 2a sin a
119
8.5. EXERCICES
.
8. Si 2 tan a = 3 tan b, démontrer que tan(a − b) =
sin 2b
5 − cos 2b
9. On donne tan a = 3 (et a ∈ QI . Calculer cos 3a.
p
√
2− 2
10. Sachant que cos x =
et x ∈ QIV , calculer les nombres trigonométriques de 2x.
2
11. Factoriser les expressions
(a) sin 3a + sin 5a + 2 sin 4a
(b) cos2 2b − cos2 b
12. Simplifier les expressions
(a)
sin 4a − sin 2a
cos 6a − cos 4a
(b)
sin a + sin 3a + sin 5a
cos a + cos 3a + cos 5a
13. Démontrer en utilisant les formules de Simpson que
b+c
a+b
a+c
(a) sin a + sin b + sin c − sin(a + b + c) = 4 sin
sin
sin
2
2
2
π
2π
3π
4π
(b) cos
+ a + cos
+ a + cos
− a + cos
−a =0
5
5
5
5
14. Exercices récapitulatifs
π
(a) Si (a + b) = , vérifier que (1 + tan a)(1 + tan b) = 2.
4
b
(b) Si tan x = , vérifier que a cos 2x + b sin 2x = a.
a
(c) Calculer sin 2x sachant que sin x − cos x = 0.2.
√
√
(d) Si 4 sin2 x − 2(1 + 3) sin x + 3 = 0, calculer sin 2x, cos 2x et tan 2x.
(e) Si tan a = 4 et a ∈ QI , calculer sin 4a.
(f) Vérifier 4(cos6 a + sin6 a) = 1 + 3 cos2 2a.
(g) Vérifier (cos a − cos b)2 + (sin a − sin b)2 = 4 sin2
a−b
.
2
(h) Vérifier sin 3a = 4 sin a sin(60◦ + a) sin(60◦ − a).
(i) Vérifier tan 3a − tan 2a − tan a = tan 3a tan 2a tan a.
sin 2a + sin 5a − sin a
(j) Montrer que
= tan 2a.
cos 2a + cos 5a + cos a
(k) Montrer que cos 80◦ + cos 40◦ − cos 20◦ = 0.
(l) Simplifier cos2 (a + b) + cos2 (a − b) − cos 2a cos 2b.
120
CHAPITRE 8. FORMULES DE TRANSFORMATION
Chapitre 9
Equations et inéquations trigonométriques
9.1
Définition
Définition: Une équation (inéquation) trigonométrique est une équation (inéquation) dans laquelle la variable apparaît dans
une fonction trigonométrique.
Résoudre une équation (inéquation) trigonométrique
consiste à trouver les valeurs des angles (exprimés en radians) vérifiant l’égalité (inégalité) proposée.
9.2
Equations trigonométriques élémentaires
Toute équation trigonométrique, aussi complexe soit elle, se ramène toujours à la résolution
d’une équation élémentaire. Ces équations sont étudiées ci-dessous.
9.2.1
Equation élémentaire du type sin x = sin a
Dans l’équation
sin x = sin a
x est l’inconnue et a un angle réel connu.
Résoudre cette équation revient à rechercher les valeurs de l’angle x dont le sinus est égal à une
valeur connue (sin a). Visualisons cette équation dans le cercle trigonométrique suivant.
Figure 9.1 – Equation élémentaire sin x = sin a
121
122
CHAPITRE 9. EQUATIONS ET INÉQUATIONS TRIGONOMÉTRIQUES
D’après la figure, on voit que les angles x pour lesquels le sinus vaut sin a sont a et π − a
Les solutions de l’équation sont donc
x = a + 2kπ
sin x = sin a ⇔
x = (π − a) + 2kπ
9.2.2
k∈Z
Equation élémentaire du type cos x = cos a
Dans l’équation
cos x = cos a
x est l’inconnue et a un angle réel connu.
Résoudre cette équation revient à rechercher les valeurs de l’angle x dont le cosinus est égal à une
valeur connue (cos a). Visualisons cette équation dans le cercle trigonométrique suivant.
Figure 9.2 – Equation élémentaire cos x = cos a
D’après la figure, on voit que les angles x pour lesquels le cosinus vaut cos a sont a et −a
Les solutions de l’équation sont donc
cos x = cos a ⇔
9.2.3
x = a + 2kπ
x = −a + 2kπ
k∈Z
Equation élémentaire du type tan x = tan a
Dans l’équation
tan x = tan a
x est l’inconnue et a un angle réel connu.
Résoudre cette équation revient à rechercher les valeurs de l’angle x dont le tangente est égal à
une valeur connue (tan a).
9.3. EQUATIONS TRIGONOMÉTRIQUES QUELCONQUES
123
Visualisons cette équation dans le cercle trigonométrique suivant.
Figure 9.3 – Equation élémentaire tan x = tan a
D’après la figure, on voit que les angles x pour lesquels la tangente vaut tan a sont a et π + a
Les solutions de l’équation sont donc
tan x = tan a ⇔ x = a + kπ k ∈ Z
9.3
9.3.1
Equations trigonométriques quelconques
Classification des équations trigonométriques
Equations générales
La plupart des équations trigonométriques ne sont pas fondamentales. Cependant, par quelques
modifications souvent simples, il est possible de s’y ramener.
On essayera de transformer l’équation en une autre ne contenant plus qu’un seul nombre trigonométrique d’un seul angle inconnu. En prenant ce nombre trigonométrique comme inconnue
auxiliaire, on obtient une équation algébrique à une inconnue.
On veillera en outre à discuter les solutions en fonction des limites entre lesquelles peuvent varier
les nombres trigonométriques.
Pour résoudre une équation trigonométrique quelconque, on pourra utiliser :
1. Les relations trigonométriques fondamentales :
sin2 x + cos2 x = 1
1
1 + tan2 x =
cos2 x
1
1 + cot2 x =
sin2 x
124
CHAPITRE 9. EQUATIONS ET INÉQUATIONS TRIGONOMÉTRIQUES
2. Les angles associés
Angles supplémentaires
Angles anti-supplémentaires
sin(π − α) = sin α
cos(π − α) = − cos α
tan(π − α) = − tan α
cot(π − α) = − cot α
sin(π + α) = − sin α
cos(π + α) = − cos α
tan(π + α) = tan α
cot(π + α) = cot α
Angles opposés
Angles complémentaires
sin(−α) = − sin α
cos(−α) = cos α
tan(−α) = − tan α
cot(−α) = − cot α
sin
cos
tan
cot
π
− α = cos α
2
π
− α = sin α
2
π
− α = cot α
2
π
−
α = tan α
2
3. Les formules de transformation
(a) Formules de duplication
cos 2a = cos2 a − sin2 a
cos 2a = 2 cos2 a − 1
cos 2a = 1 − 2 sin2 a
sin 2a = 2 sin a cos a
2 tan a
tan 2a =
1 − tan2 a
(b) Formules d’addition
cos(a + b) = cos a cos b − sin a sin b
cos(a − b) = cos a cos b + sin a sin b
sin(a + b) = sin a cos b + cos a sin b
sin(a − b) = sin a cos b − cos a sin b
tan a + tan b
tan(a + b) =
1 − tan a tan b
tan a − tan b
tan(a − b) =
1 + tan a tan b
(c) Formules de Simpson
p+q
p−q
cos
2
2
p+q
p−q
sin p − sin q = 2 cos
sin
2
2
p+q
p−q
cos p + cos q = 2 cos
cos
2
2
p+q
p−q
cos p − cos q = −2 sin
sin
2
2
sin p + sin q = 2 sin
(d) Formules de Carnot
1 + cos 2a
2
1 − cos 2a
2
sin a =
2
cos2 a =
9.3. EQUATIONS TRIGONOMÉTRIQUES QUELCONQUES
125
4. Les techniques classiques de factorisation (mise en évidence, équation du second degré,
produits remarquables, )
Ces techniques permettent en général de transformer l’équation initiale en équation produit du
type :
A(x).B(x) = 0
où A(x) et B(x) sont des équations trigonométriques élémentaires du style de celles exposées au
paragraphe 9.2.
Remarque importante : On devra toujours poser les conditions d’existence et de simplification de
l’équation sous peine d’obtenir des solutions inacceptables.
Equation en sin x et cos x
1. Si l’équation ne contient que des puissances paires de sin x et cos x, on utilise la relation
fondamentale de la trigonométrie : sin2 x + cos2 x = 1 pour remplacer sin x par cos x ou vice
versa.
2. Si l’équation est homogène en sin x et cos x, c’est à dire qu’elle comporte des termes en sin x,
cos x et sin x cos x, il suffit de diviser les deux membres l’équation par cos2 x et de passer à
l’inconnue auxiliaire tan x 1 .
π
Attention, dans ce cas, il faut imposer x 6= + kπ pour que l’équation continue d’exister.
2
Equation du type a cos x + b sin x = c
Dans cette équation, a et b sont des réels non nuls.
Puisque a 6= 0, on peut diviser les deux membres de l’équation par a.L’équation devient
cos x +
ou encore, en posant
c
b
sin x =
a
a
b
= tan φ
a
c
cos x + tan φ sin x =
a
sin φ
c
⇔ cos x +
sin x =
cos φ
a
c
⇔ cos φ cos x + sin φ sin x = cos φ
a
Finalement, on peut écrire à l’aide des formules d’addition :
cos(x − φ) =
c
cos φ
a
Cette relation est valable pour autant que
c
cos φ ≤ 1
a
ou encore, après élévation au carré
c 2 ≤ a2 + b 2
1. en utilisant le fait que 1 + tan2 x =
1
sin x
et tan x =
cos2 x
cos x
126
CHAPITRE 9. EQUATIONS ET INÉQUATIONS TRIGONOMÉTRIQUES
L’équation devient donc une équation fondamentale (φ est connu) dont la solution est

c cos φ

−1

+ 2kπ
 x − φ = cos
a
k∈Z
c cos φ


+ 2kπ
 x − φ = − cos−1
a
ou encore

c cos φ

−1

+ φ + 2kπ
 x = cos
a
c cos φ


+ φ + 2kπ
 x = − cos−1
a
k∈Z
Exemples
1. Soit à résoudre sin x = sin 3x.
Cette équation peut s’apparenter à une équation élémentaire. On a donc
(
x = kπ
x = 3x + 2kπ
π
π k∈Z
sin x = sin 3x ⇔
⇔
x= +k
x = (π − 3x) + 2kπ
4
2
Remarque : on aurait pu également résoudre cette équation à l’aide des formules de Simpson.
En effet, on a successivement :
sin x = sin 3x
⇔ sin x − sin 3x = 0
⇔ cos 2x sin x = 0
qui est une équation produit dont les solutions sont
(
x = kπ
π k∈Z
π
⇔
x= +k
4
2
2. Soit à résoudre sin x = − cos x.
Les angles associés permettent d’écrire l’équation sous la forme :
π
+x
sin x = sin
2
dont les solutions sont :

 x = π + x + 2kπ
2
 x = π − π + x + 2kπ
2
La première équation est impossible, la seconde donne :
x=
π
+ kπ k ∈ Z
4
k∈Z
9.3. EQUATIONS TRIGONOMÉTRIQUES QUELCONQUES
127
7
.
3. Soit à résoudre 3 tan2 x + 5 =
cos x
Les conditions d’existence de tan x impose que
x 6=
π
+ kπ
2
Les relations fondamentales de la trigonométrie permettent d’écrire l’équation sous la forme :
7
1
−1 +5=
3
2
cos x
cos x
ou encore, en simplifiant, en réduisant au même dénominateur et en simplifiant par cos x 2 :
2 cos2 x − 7 cos x + 3 = 0
En posant y = cos x, l’équation devient
2y 2 − 7y + 3 = 0
dont la solution est :
(
y=3
1
y=
2
La première solution est à rejeter puisque y représente un cosinus qui doit toujours être
inférieur à 1. La seconde donne, en repassant à l’inconnue x :

 x = π + 2kπ
3
k∈Z
 x = − π + 2kπ
3
x
4. Soit à résoudre l’équation 2 cos x + 3 = 4 cos .
2
Les formules de duplication (appliquées à l’angle x) donne :
4 cos2
x
x
− 4 cos + 1 = 0
2
2
En appliquant la même technique que pour l’exemple précédent, on obtient les solutions :


 x = 2π + 4kπ
3
k∈Z
2π

 x=−
+ 4kπ
3
5. Soit à résoudre l’équation sin4 x + cos4 x = 1.
La formule fondamentale de la trigonométrie permet d’écrire, après simplification, l’équation
sous la forme :
2 cos2 x 1 − cos2 x = 0
dont les solutions sont
2. puisque x 6=
π
+ kπ
2
(
π
+ kπ
2
x = kπ
x=
k∈Z
128
CHAPITRE 9. EQUATIONS ET INÉQUATIONS TRIGONOMÉTRIQUES
6. Soit à résoudre l’équation sin2 x + sin x cos x − cos2 x = 0.
En divisant les deux membres de l’équation par cos2 x 3 et en tenant compte du fait que
sin x
1
et tan x =
, on a
1 + tan2 x =
2
cos x
cos x
tan2 x + tan x − 1 = 0
En posant y = tan x et en résolvant cette équation, on obtient :

√ !

−1
+
5

−1

+ kπ

 x = tan
2
√ !
k∈Z

−1
−
5

−1

+ kπ

 x = tan
2
Remarque : il peut arriver que les valeurs obtenues comme solution ne soit pas des valeurs
remarquables ! !
√
7. Soit à résoudre l’équation cos x + 3 sin x = 1.
√
π
On pose tan φ = 3 et donc φ = . L’équation devient :
3
π
cos x + tan sin x = 1
3
π
3 sin x = 1
⇔ cos x +
π
cos
3
sin
π
π
π
cos x + sin sin x = cos
3
3
3
π
π
= cos
⇔ cos x −
3
3
⇔ cos
dont les solution sont
ou encore
9.4

π
π


 x − 3 = 3 + 2kπ
k∈Z

π
π

 x − = − + 2kπ
3
3

2π

 x=
+ 2kπ
3
k∈Z


x = 2kπ
Inéquations trigonométriques
Le résolution d’inéquations trigonométriques est quelque peu plus complexe que celle des
inéquations algébriques. En effet, l’existence de racines multiples d’une fonction trigonométrique
complique la construction du tableau de signe lié à l’inéquation. Cependant, le cercle trigonométrique permet de réduire ce problème.
Quelques exemples vous nous permettre de saisir les techniques de résolution des inéquations
trigonométriques.
3. x 6=
π
+ kπ
2
9.4. INÉQUATIONS TRIGONOMÉTRIQUES
9.4.1
129
Remarque préliminaire
Depuis la 4ème, on sait que tous les angles sont donnés à 2π près. Dès lors, on est souvent
amené à travailler en valeur principale des angles, c’est-à-dire les valeurs d’angles comprises dans
l’intervalle [0, 2π[ ou, pour des raisons qui apparaitront dans le cadre de l’étude des fonctions
trigonométriques 4 dans l’intervalle
[−π, π[
Dès lors toutes les solutions des inéquations trigonométriques seront toujours précisées dans ce
dernier intervalle
9.4.2
Inéquations trigonométriques simples
Premier exemple
Soit à résoudre l’inéquation
1
2
La représentation de cette inéquation sur le cercle trigonométrique est la suivante :
sin x ≤
La solution de cette inéquation 5 est
πi
5π
x ∈ −π,
∪
, π (+2kπ, k ∈ Z)
6
6
h
Deuxième exemple
Soit à résoudre l’inéquation
4. Voir cours d’analyse de 6ème
5. représentée en vert sur la figure
π √
tan 3x +
> 3
2
130
CHAPITRE 9. EQUATIONS ET INÉQUATIONS TRIGONOMÉTRIQUES
La représentation de cette inéquation sur le cercle trigonométrique est la suivante :
La solution de cette inéquation 6 est
π iπ π h
∈
,
(+kπ, k ∈ Z)
3x +
2
3 2
ou, en décallant l’intervalle de −
π
2
−π
3x ∈
, 0 (+kπ, k ∈ Z)
6
et, enfin, en divisant par 3 :
kπ
−π
, 0 (+ , k ∈ Z)
x∈
18
3
Troisième exemple
Soit à résoudre l’inéquation
tan
3π
− tan 2x ≥ 0
5
Cette inéquation peut encore s’écrire :
tan 2x ≤ tan
6. représentée en vert sur la figure
3π
5
131
9.4. INÉQUATIONS TRIGONOMÉTRIQUES
La représentation de cette inéquation sur le cercle trigonométrique est la suivante
La solution de cette inéquation 7 est
π 3π
2x ∈
,
(+kπ, k ∈ Z)
2 5
et, enfin, en divisant par 2 :
π 3π
x∈
,
4 10
7. représentée en vert sur la figure
(+
kπ
, k ∈ Z)
2
132
CHAPITRE 9. EQUATIONS ET INÉQUATIONS TRIGONOMÉTRIQUES
9.4.3
Inéquations trigonométriques complexes
Les techniques de résolution d’inéquations complexes passent toujours par une factorisation
complète (facteurs du premier ou du second degré) de l’inéquation afin d’être capable d’appliquer
les techniques vues au paragraphe 9.4.2
Premier exemple
Soit à résoudre l’inéquation
cos 2x + cos x ≤ 0
En procédant de même que pour les équations trigonométriques 8 , l’inéquation peut s’écrire :
2 cos2 x − 1 + cos x ≤ 0
ou encore
2 cos2 x + cos x − 1 ≤ 0
Si on pose y = cos x, l’inéquation se ramène à une simple inéquation algébrique du second degré
2y 2 + y1 ≤ 0
dont la solution est donnée par :
1
−1
y
2
2y 2 + y − 1 + 0 − 0 +
ou :
1
−1 ≤ y ≤ ]
2
ou encore, en terme de cos x :
1
−1 ≤ cos x ≤ ]
2
Le cercle trigonométrique permet de trouver la solution de cette inéquation (en vert sur la figure)
On trouve :
h
π i hπ h
x ∈ −π, − ∪ , π (+2kπ, k ∈ Z)
3
3
8. voir à ce sujet le paragraphe 9.3.1
133
9.4. INÉQUATIONS TRIGONOMÉTRIQUES
Deuxième exemple
Soit à résoudre l’inéquation
sin 3x + cos x > 0
On a successivement :
sin 3x + sin
π
2
−x >0
et, par les formules de Simpson :
π




π
3x −
3x + − x
−x
2
2
 cos 
>0
2 sin 
2
2
et enfin :
π
π
2 sin x +
cos 2x −
>0
4
4
Cette inéquation est vérifiée lorsque les deux facteurs sont du même signe, c’est à dire si


 sin x + π > 0
 sin x + π < 0
4 4 ou
 cos 2x − π > 0
 cos 2x − π < 0
4
4
Nous sommes donc ici en présence d’un système de deux inéquations relativement élémentaires à
une inconnue.
Intéressons-nous au premier cas :

 sin x + π > 0
4  cos 2x − π > 0
4
ou 9

 x + π ∈ ]0, π[ (+2kπ, k ∈ Z)
4
i
h
 2x − π ∈ − π , π (+2kπ, k ∈ Z)
4
2 2
et enfin

π 3π


(+2kπ, k ∈ Z)
 x∈ − ,
4 4
π 3π


(+kπ, k ∈ Z)
 x∈ − ,
8 8
La compatibilité de ce système est déterminé graphiquement par :
ou :
π 3π
S1 : x ∈ − ,
8 8
(+2kπ, k ∈ Z)
9. à l’aide du signe des fonctions trigonométriques de base et du cercle trigonométrique
134
CHAPITRE 9. EQUATIONS ET INÉQUATIONS TRIGONOMÉTRIQUES
Le second cas est le complément du précédent. Sa solution est donc :

i
πh
3π


, π (+2kπ, k ∈ Z)
 x ∈ −π, − ∪
4
4
3π 7π


,
(+kπ, k ∈ Z)
 x∈
8 8
La compatibilité de ce système est déterminé graphiquement par :
ou :
3π 7π
5π π
∪
,
(+2kπ, k ∈ Z)
S2 : x ∈ − , −
8
4
8 8
La solution générale l’inéquation :
sin 3x + cos x > 0
est la réunion des deux solution strouvées précédemment, soit :
S = S1 ∪ S2
135
9.5. EXERCICES
9.5
Exercices
1. Résoudre graphiquement les équations suivantes :
√
√
2
(c) 1 + 2 cos x = 0
(a) sin x =
2√
√
(d) 2 3 sin x + 3 = 0
(b) tan x = − 3
2. Résoudre les équations suivantes
(a) sin x =
1
4
cot x cot x
1
−
=
5
3
4
√
(c) 12 cos x = cos x − 2
(b)
3. Résoudre les équations suivantes (techniques diverses) 10
(a) *tan 3x = −1
(b) cot 3x = cot x
π
1
(c) cos 2x −
=−
3
2
(d) *sin x = cos x
(e) tan x cot 4x = 1
(f) *3 tan2 x = 1
(g) 2 cos2 x = cos x
(h) *2 sin2 x − 3 sin x + 1 = 0
(i) *3 cos2 x = 7(1 − sin x)
(j) tan2 x + cot2 x = 4
(k) *sin 2x + tan 2x = 0
(l) *cos 2x = cos x + 1
(m) *3 cos x(sin x + tan x) = 2(1 + cos x)
(n) *5 sin2 x − 2 cos2 x − 3 sin x cos x = 0
(o) *sin x + cos x = 1
√
(p) *cos x + 3 sin x = 1
√
√
(q) 2 cos x − 2 sin x = 1
(r) 2 sin x − 3 cos x = 3
10. Les exercices marqués d’une * doivent être réalisés, les autres servent d’entrainement
136
CHAPITRE 9. EQUATIONS ET INÉQUATIONS TRIGONOMÉTRIQUES
4. Résoudre les inéquations suivantes :
√
3
(a) cos x >
2√
(b) 3 tan y − 3 ≥ 0
(c) 1 − 3 sin x ≤ 0
(d) 2 sin 3t + 1 < 0
3π
(e) tan
− tan 2x ≥ 0
5
3
(f) sin2 3x ≤
4
9.6
(g) 2 |cos x| − 1 > 0
(h) 2 sin2 x − 3 sin x + 1 < 0
2 sin 2x − 1
>0
cos 2x − 3 cos x + 2
√
√
(j) tan2 2x + (1 − 3) tan 2x − 3 ≤ 0
(i)
(k) sin 3 − sin 2x + sin x ≥ 0
Solutions
π 3π
1. (a) S =
,
+ 2kπ (k ∈ Z)
4 4
n πo
(b) S = −
+ kπ (k ∈ Z)
3
3π 3π
(c) S = −
,
+ 2kπ (k ∈ Z)
4 4
π 4π
(d) S = − ,
+ 2kπ (k ∈ Z)
3 3
2. Résoudre les équations suivantes
(a) S = {0.253; 2.889} + 2kπ (k ∈ Z)
(b) S = {−0.49} + kπ (k ∈ Z)
(c) S = {−2.518; 2.518} + 2kπ (k ∈ Z)
3. Résoudre les équations suivantes (techniques diverses) 11
nπ o
n π o kπ
(i)
S
=
+ 2kπ (k ∈ Z)
(a) S = −
+
(k ∈ Z)
2
12
3
(j) S = {−1.093; −0.478; 0.478; 1.093} +
(2k + 1)π
(b) S =
(k ∈ Z) (attention
kπ (k ∈ Z)
2
kπ
au C.E.)
(k) S =
(k ∈ Z)
n π π o kπ
2
(c) S = − ,
+
(k ∈ Z)
(l) S = {−2.467; 2.467} + 2kπ (k ∈ Z)
6 2
3
π 5π
(m) S = {0.73; 2.41; π} + 2kπ (k ∈ Z)
(d) S =
,
+ 2kπ (k ∈ Z)
n
πo
4 4
(n) S = −0.38;
+ kπ (k ∈ Z)
kπ
n πo 4
(e) S = −
(k ∈ Z)
(o) S = 0,
+ 2kπ (k ∈ Z)
3
2
n π πo
2π
(f) S = − ,
+ kπ (k ∈ Z)
(p) S = 0,
+ 2kπ (k ∈ Z)
6 6
3
n π
o
π π π
(g) S = − , − , ,
+ 2kπ (k ∈ Z)
π
7π
2
3 3 2
(q) S =
,
+ 2kπ (k ∈ Z)
12 12
π π 5π
(h) S =
, ,
+ 2kπ (k ∈ Z)
(r) S = {1.966; π} + 2kπ (k ∈ Z)
6 2 6
4. (a)
11. Les exercices marqués d’une * doivent être réalisés, les autres servent d’entrainement
Cinquième partie
Annexes
137
139
.1. FORMULAIRE DE TRIGONOMÉTRIE
.1
Formulaire de trigonométrie
y
1J
cot α
A tan α
sin α
0
α
cos α
x
I
1
1. Angles remarquables
α
0
π
6
sin α
0
1
2
cos α
1
tan α
0
cot α
∞
√
3
2
√
3
3
√
3
π
4
π
3
√
√
2
2
√
2
2
1
1
π
2
π
3π
2
3
2
1
0
-1
1
2
0
-1
0
∞
0
∞
0
∞
0
√
3
√
3
3
2. Angles associés
Angles supplémentaires
Angles anti-supplémentaires
sin(π − α) = sin α
cos(π − α) = − cos α
tan(π − α) = − tan α
cot(π − α) = − cot α
sin(π + α) = − sin α
cos(π + α) = − cos α
tan(π + α) = tan α
cot(π + α) = cot α
Angles opposés
Angles complémentaires
sin(−α) = − sin α
cos(−α) = cos α
tan(−α) = − tan α
cot(−α) = − cot α
3. Identités fondamentales
sin
cos
tan
cot
π
− α = cos α
2
π
− α = sin α
2
π
− α = cot α
2
π
− α = tan α
2
sin2 a + cos2 a = 1
1
1 + tan2 a =
cos2 a
1
2
1 + cot a =
sin2 a
140
4. Formules de duplication
cos 2a = cos2 a − sin2 a
cos 2a = 2 cos2 a − 1
cos 2a = 1 − 2 sin2 a
sin 2a = 2 sin a cos a
2 tan a
tan 2a =
1 − tan2 a
5. Formules d’addition
cos(a + b) = cos a cos b − sin a sin b
cos(a − b) = cos a cos b + sin a sin b
sin(a + b) = sin a cos b + cos a sin b
sin(a − b) = sin a cos b − cos a sin b
tan a + tan b
tan(a + b) =
1 − tan a tan b
tan a − tan b
tan(a − b) =
1 + tan a tan b
6. Formules de Simpson
p+q
p−q
cos
2
2
p−q
p+q
sin
sin p − sin q = 2 cos
2
2
p+q
p−q
cos p + cos q = 2 cos
cos
2
2
p−q
p+q
sin
cos p − cos q = −2 sin
2
2
sin p + sin q = 2 sin
7. Formules de Carnot 12
1 + cos 2a
2
1 − cos 2a
2
sin a =
2
cos2 a =
8. Formules de Simpson inverses 13
1
sin a sin b = − (cos(a + b) + cos(a − b))
2
1
sin a cos b = (sin(a + b) + sin(a − b))
2
1
cos a cos b = (cos(a + b) + cos(a − b))
2
9. Equations trigonométriques
x = a + 2kπ
sin x = sin a ⇔
k∈Z
x = π − a + 2kπ
cos x = cos a ⇔
x = a + 2kπ
x = −a + 2kπ
tan x = tan a ⇔ x = a + kπ k ∈ Z
12. Utiles en math 8h
13. Utiles en math 8h
k∈Z
141
.1. FORMULAIRE DE TRIGONOMÉTRIE
Résumé
y
√
− 3
√
-1
−
3
3
1
√
√
J
√
3
2
C 0 (2π/3)
3
√
1
3
3
3
C(π/3)
√
2
2
B 0 (3π/4)
B(π/4)
3
3
1
2
A0 (5π/6)
−
√
3
2
√
−
2
2
− 12
√
A(π/6)
1
2
O
√
2
2
√
3
2
x
I
1
0
A00 (7π/6)
A000 (11π/6)
− 12
B 00 (5π/4)
√
2
2
√
− 23
√
B 000 (7π/4) −
3
3
−
C 00 (4π/3)
C 000 (5π/3)
-1
√
− 3
142
.2
Fomrulaire de dérivées
Formules générales
(f (x) ± g(x))0 = f (x)0 ± g(x)0
(f (x).g(x))0 = f (x)0 g(x) + f (x)g(x)0
0
f (x)0 g(x) − f (x)g(x)0
f (x)
=
g(x)
g(x)2
(kf (x))0 = kf (x)0
Formules particulières
(k)0 = 0
(x)0 = 1
(xn )0 = nxn−1
√ 0
1
( x) = √
2 x
0
1
1
=− 2
x
x
(f (x)n )0 = nf (x)n−1 f (x)0
0
p
f (x)0
f (x) = p
2 f (x)
0
f (x)0
1
=− 2
f (x)
f (x)
(cos x)0 = − sin x
(sin x)0 = cos x
(cos f (x))0 = − sin f (x)f (x)0
(sin f (x))0 = cos f (x)f (x)0
1
cos2 x
1
(cot x)0 = − 2
sin x
f (x)0
cos2 f
f (x)0
0
(cot f (x)) = − 2
sin f
(tan x)0 =
(tan f (x))0 =
1
1 − x2
1
(arccos x)0 = − √
1 − x2
f (x)0
p
(arcsin f (x)) =
1 − f 2 (x)
f (x)0
(arccos f (x))0 = − p
1 − f 2 (x)
0
(arcsin x) = √
(arctan x)0 =
(ln x)0 =
1
1 + x2
1
x
(loga x)0 =
0
(arctan f (x))0 =
f (x)0
1 + f 2 (x)
f (x)0
f (x)
f (x)0
(loga f (x))0 =
f (x). ln a
(ln f (x))0 =
1
x. ln a
(ex )0 = ex
(ef (x) )0 = ef (x) .f (x)0
(ax )0 = ax . ln a
(af (x) )0 = af (x) . ln a.f (x)0
Table des figures
3.1
Graphe de la fontion
x3 + 1
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
x
31
4.1
Accroissement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
47
4.2
Sécante à une courbe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
48
4.3
Tangente à une courbe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
49
5.1
Maximum et minimum, croissance et décroissance . . . . . . . . . . . . . . . . . .
63
6.1
Définition d’un vecteur . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
87
6.2
Egalité de vecteur . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
88
6.3
Relation de Chasles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
89
6.4
Relation de Chasles généralisée . . . . . . . . . . . . . . . . . . . . . . . . . . . .
90
6.5
Somme de deux vecteurs quelconques . . . . . . . . . . . . . . . . . . . . . . . . .
90
6.6
Somme de deux vecteurs de même origine . . . . . . . . . . . . . . . . . . . . . .
91
6.7
Différence de deux vecteurs
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
91
6.8
Multiplication d’un vecteur par un réel . . . . . . . . . . . . . . . . . . . . . . . .
92
6.9
Vecteurs parallèles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
93
6.10 Points alignés . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
93
6.11 Composantes d’un vecteur . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
95
6.12 Milieu d’un segment . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
97
7.1
Trigonométrie dans le triangle rectangle . . . . . . . . . . . . . . . . . . . . . . . . 105
7.2
Le cercle trigonométrique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 106
7.3
Quadrants du cercle trigonométrique . . . . . . . . . . . . . . . . . . . . . . . . . 107
7.4
Lecture du cosinus et du sinus d’un angle orienté
7.5
Lecture de la tangente et de la cotangente d’un angle orienté . . . . . . . . . . . . 108
7.6
Signe des nombres trigonométriques . . . . . . . . . . . . . . . . . . . . . . . . . . 108
9.1
Equation élémentaire sin x = sin a . . . . . . . . . . . . . . . . . . . . . . . . . . . 121
9.2
Equation élémentaire cos x = cos a . . . . . . . . . . . . . . . . . . . . . . . . . . . 122
9.3
Equation élémentaire tan x = tan a . . . . . . . . . . . . . . . . . . . . . . . . . . 123
143
. . . . . . . . . . . . . . . . . . 107
144
TABLE DES FIGURES