marginal -"et le"

Tle ES Calcul intégral – Collège de Juilly – H. Kerneïs
1
CALCUL INTEGRAL
1. Aire sous une courbe
1.1. Unité d’aire dans un repère orthogonal
On considère
O;OI,OJ
()
un repère orthogonal. K est le point de coordonnées
1;1
()
dans ce repère. L’unité d’aire est l’aire du rectangle OIKJ.
Exemples :
i. L’aire du rectangle ABCD ci-dessus est de 2 unités d’aires.
OI = 2 cm et OJ = 3 cm, donc l’aire de ABCD est
2  2  3 = 12 cm2.
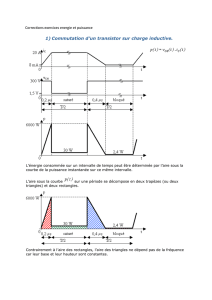
ii. Dans une entreprise de fabrication d’objets, le coût marginal varie par
paliers. Le graphique ci-dessous représente ces variations en fonction du
nombre d’unités déjà produites.

Tle ES Calcul intégral – Collège de Juilly – H. Kerneïs
2
On admet que le coût total (en Euros) pour la fabrication de 1200
unités correspond à l’aire sous la courbe sur l’intervalle [0 ; 1200].
La fonction coût marginal est positive sur [0 ; 1200]. L’aire du domaine
cherché (en gris) est, en unités d’aire :
4 200 0
()
+3 500 200
()
+2 1000 500
()
+5 1200 1000
()
=3700
.
Donc le coût total de fabrication de 1200 unités est de 3700 .
1.2. Notion d’intégrale
Définition 1 : f est une fonction continue sur un intervalle ouvert I, a et b sont
deux réels de I. De plus F est l’une des primitives de f.
On appelle intégrale de f entre a et b le nombre
Fb
()
Fa
()
.
On note ce réel
fx
()
dx
a
b
.
Remarques :
i. Ce nombre se lit « somme de a à b de
fx
()
dx
» ou « intégrale de a à b de
fx
()
dx
».
ii. Ce nombre ne dépend pas de la primitive choisie. En effet, avec les notations
précédentes, les autres primitives de f sont de la forme
Gx
()
=Fx
()
+k
avec
k un nombre réel. Et l’on remarque que
Gb
()
Ga
()
=Fb
()
Fa
()
.
iii. Dans la pratique, pour calculer
fx
()
dx
a
b
, on détermine une primitive F de
f sur un intervalle contenant a et b, puis on écrit :
fx
()
dx
a
b
=Fx
()
a
b
=Fb
()
Fa
()
.
Exemple :
x
2
dx
1
2
=x
3
3
1
2
=2
3
31
3
3=7
3
.
Propriété 1 :
i.
fx
()
dx
a
a
=0
.
ii.
fx
()
dx
b
a
=fx
()
dx
a
b
.
Preuve : avec les notations précédentes…
i.
fx
()
dx
a
a
=Fa
()
Fa
()
=0
.
ii.
fx
()
dx
b
a
=Fa
()
Fb
()
=Fb
()
Fa
()
()
=fx
()
dx
a
b
.

Tle ES Calcul intégral – Collège de Juilly – H. Kerneïs
3
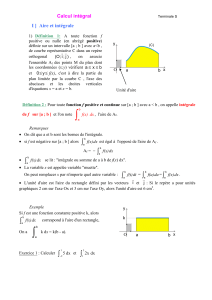
1.3. Intégrale et aire sous une courbe
Propriété 2 : admise…
f est une fonction continue et positive sur un intervalle I. a et b sont deux réels
de I tels que a  b. C est la courbe représentative de f dans un repère
orthogonal.
fx
()
dx
a
b
est l’aire, en unités d’aire, du domaine compris entre la courbe C,
l’axe des abscisses et les droites d’équations x = a et x = b.
Remarques :
i. On dit aussi de manière moins rigoureuse que c’est l’aire sous la courbe C
entre a et b.
ii. On pourrait approcher l’aire sous la courbe en ajoutant les aire
fx
()
dx
de
tous les rectangles de dimensions dx (aussi petit que l’on veut) et
fx
()
.
Exemple : C est la courbe représentative de la fonction
x1
x
sur
l’intervalle
0;+
. On désigne par
st
()
l’aire, en unités d’aire, sous
cette courbe entre 1 et t. On a :
Si t  1,
st
()
=dx
x
1
t
=lnx
1
t=lnt
.
Si 0 < t  1,
st
()
=dx
x
t
1
=lnx
t
1=lnt
.
2. Valeur moyenne d’une fonction sur un intervalle
Définition 2 :
f est une fonction continue sur un intervalle I. a et b sont deux réels de I tels que
a < b. La valeur moyenne de f sur l’intervalle [a ; b] est le réel :
1
bafx
()
dx
a
b
.

Tle ES Calcul intégral – Collège de Juilly – H. Kerneïs
4
Interprétation géométrique : cas où f est positive sur [a ; b].
C est la courbe représentative de f dans un repère orthogonal. En unités d’aire :
fx
()
dx
a
b
est l’aire sous cette courbe entre a et b ;
et
mba
()
est l’aire du rectangle ABCD (en gris sur le dessin).
Donc m, valeur moyenne de f sur [a ; b], est la « hauteur » du rectangle de base
ba
()
ayant la même aire que le domaine sous la courbe C entre a et b.
Remarque : m a la même unité que la fonction f.
Exemples :
i. Le débit en m3/h d’une pompe à arrosage qui fonctionne en été de 6
heures à 20 heures, est modélisé par
fx
()
=5e
0,002x
où x est l’heure
considérée (6  x  20). Une primitive F de f est :
Fx
()
=51
0,002 e0,002x=2500e0,002x
.
Le volume d’eau débité par cette pompe entre 6 heures et 20 heures est
fx
()
dx
6
20
=F20
()
F6
()
 71,85 m3.
Le débit moyen de cette pompe entre 6 et 20 heures est égal à :
1
20 6fx
()
dx
6
20
5,13
m3/h.
Ce nombre est la valeur moyenne de la fonction f, il est donc exprimé
dans la même unité.
ii. Dans une région où une épidémie commence à se propager, on
constate que le nombre de malades contaminés t jours après le début de
l’épidémie est M(t).
Le nombre total de malades sur une période de 30 jours est
Mt
()
dt
0
30
.
Le nombre moyen de personnes contaminées par jour est
1
30 Mt
()
dt
0
30
.

Tle ES Calcul intégral – Collège de Juilly – H. Kerneïs
5
3. Propriétés de l’intégrale
f et g sont des fonctions continues sur un intervalle I, a et b sont deux réels quelconques.
3.1. Linéarité
Théorème 1 :
i.
fx
()
+gx
()
()
dx
a
b
=fx
()
dx
a
b
+gx
()
dx
a
b
.
ii.
kf x
()
dx
a
b
=kfx
()
dx
a
b
pour tout réel k.
Preuve :
i. Soient F et G des primitives respectives de f et g sur I. Alors
F + G est une primitive de f + g sur I. (Voir chapitre sur les
primitives.) Ainsi :
fx
()
+gx
()
()
dx
a
b
=Fx
()
+Gx
()
a
b
=Fb
()
+Gb
()
Fa
()
+Ga
()
=Fb
()
Fa
()
+Gb
()
Ga
()
=fx
()
dx
a
b
+gx
()
dx
a
b
ii. De manière analogue car kF est une primitive de kf sur I.
Exemple : Calculer
4t
2
+3e
t
()
dt
0
1
.
3.2. Positivité et ordre
Théorème 2 : a et b sont deux réels de I tels que a  b.
Si pour tout x de [a ; b],
fx
()
0
, alors
fx
()
dx
a
b
0
.
Preuve : F est une primitive de f sur I, alors pour tout x de I,
F'x
()
=fx
()
. Or
fx
()
0
sur [a ; b], donc F est une
fonction croissante sur [a ; b]. Ce qui implique que
Fa
()
Fb
()
c’est à dire
Fb
()
Fa
()
0
et donc
fx
()
dx
a
b
0
.
Théorème 3 : a et b sont deux réels de I tels que a  b.
Si pour tout x de I,
fx
()
gx
()
, alors
fx
()
dx
a
b
gx
()
dx
a
b
.