CALCUL INTÉGRAL

PhG - Calcul intégral
I- Théorèmes et définition
Théorème 1
Soit une primitive F d'une fonction f continue sur un intervalle I et un couple de réels (a ; b) de I,
le nombre réel F(b) – F(a) est indépendant du choix de la primitive F.
Démonstration :
Soit G une autre primitive de la fonction f sur I. On a G = F + C où C est une fonction constante sur I.
Le calcul de la différence G(b) – G(a) donne : G(b) – G(a) = F(b) + C – (F(a) + C) = F(b) – F(a).
Ce résultat justifie la définition suivante.
Définition
Soit f une fonction continue qui admet F comme primitive sur un intervalle I et un couple de réels
(a ; b) de I, le nombre réel F(b) – F(a) s'appelle l'intégrale de a à b de la fonction f.
Le réel F(b) – F(a) s'écrit souvent sous la forme condensée
F(t) b
a
,
L'intégrale de a à b de f se note
b
adt)t(f
b
adt(t)f
= F(b) – F(a) =
F(t) b
a
et se lit «somme de a à b de f(t) dt».
Commentaires :
1. Dans l'écriture
b
adt)t(f
, la lettre t est une variable muette qui peut être remplacée par n'importe quelle autre
lettre, hormis a, b et f déjà choisies.
2- Le symbole intégral correspond à l'écriture du XVIIè siècle, étirement de la lettre S du mot latin summa.
Théorème 2
Soit f une fonction continue sur un intervalle I, l'unique primitive de f qui s'annule en un point a
de I est la fonction définie sur I par
xf
adt)t(
.
Démonstration :
À tout réel x de l'intervalle I, on peut associer l'intégrale de a à x de f ; soit K cette fonction x :
Error!
xf
adt)t(
.
Si F est une primitive de f sur I, alors pour tout x de I,
xf
adt)t(
= F(x) – F(a) soit K (x) = F(x) – F(a).
On en déduit que K est une primitive de la fonction f car K ' (x) = F ' (x) = f(x)
On a aussi K(a) = F(a) – F(a) = 0 ; or il existe sur I, une unique primitive qui s'annule en a : K est cette primitive.
La primitive de f qui s'annule au point a de I est la fonction définie sur I par K(x) =
xf
adt)t(
.
II- Propriétés d'une intégrale
Soit f et g deux fonctions continues sur un intervalle I et a, b et c trois réels de l'intervalle I.
 Relation de Chasles
  c
b
b
a
c
adx)x(dx)x(dx)x( fff
De façon évidente on a : F(c) – F(a) = [F(b) – F(a)] – [F(c) – F(b)].

y
x
O
b
a
C
A
A '
 La relation de Chasles avec a = b = c donne :
a
adx)x(f
= 0.
 La relation de Chasles avec a = c donne :
b
a
a
bdx)x(dx)x( ff
.
 Linéarité de l'intégrale
  b
a
b
a
b
adx)x(dx)x(dx)x()( gfgf
avec  et  deux réels quelconques
 Ce qui donne aussi :
  b
a
b
adx)x(dx)x()( ff
et
  b
a
b
a
b
adx)x(dx)x(dx)x()( gfgf
.
 L'intégration, le calcul des intégrales, dispose d'une règle bien particulière nommée
intégration par parties.
Si f et g sont deux fonctions dérivables sur un intervalle I, et si f ' et g ' sont continues sur I,
alors on peut écrire, pour tout réels a et b de I :
  b
a
b
a
b
adx)x()x(')x(.)x(dx)x(')x( gfgfgf
III- Calcul d'aire
Le calcul intégral prend ses racines dans le calcul d'aires et de
volumes. Eudoxe (–408; – 355) et Archimède (–287; – 212)
donnent l'idée fondamentale : «pour trouver une aire inconnue,
on l'encadre de plus en plus finement par des aires connues».
Mais cette méthode a des limites matérielles. Les mathématiciens
ont inventé d'autres méthodes de calcul très performantes.
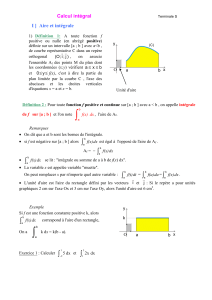
Soit f une fonction continue sur [a ; b],
C sa représentation graphique et F une primitive de f.
1- f est positive sur [a ; b]
L'aire A colorée sur la figure est :
A =
a
adx)x(f
= F(b) – F(a)
Cette aire est limitée par C, l'axe Ox et les droites
d'équation x = a et x = b.
2- f est négative sur [a ; b]
(–f) est positive sur [a ; b] et l'aire A ' est donc :
A ' = –
a
adx)x(f
= – [ F(b) – F(a)]

PhG - Calcul intégral
y
x
O
b
c
a
C
3- f change de signe sur [a ; b]
Si f change de signe un nombre fini de fois sur
[a ; b], on fait la somme des aires sur les
intervalles où f à un signe constant.
Exemple :
f change de signe en c avec f(x) 0 sur [a ; c[
et f(x) 0 sur [c ; b].
L'aire colorée sur la figure est :
A =
c
adx)x(f
+  –
b
cdx)x(f
4- Aire du domaine compris entre deux courbes
Soit g et h deux fonctions continues sur [a ; b], C 1 et C 2 leurs courbes représentatives.
On pose f = g – h et on est ramené aux cas précédents.
IV- Valeur moyenne d'une fonction
Soit f une fonction continue sur l'intervalle [a ; b] avec a < b.
La valeur moyenne de f sur [a ; b] est le réel :
b
adt)t(
ab 1f
.
Commentaires :
 Interprétations en physique
1. Lorsque v est la vitesse instantanée d'un mobile en mouvement, la fonction x : t
Error!
l(t), où l(t) est la distance
parcourue à l'instant t, est une primitive de v (v = dl
dt). Le réel
b
adt)t(
ab 1v
peut s'écrire l(b) – l(a)
b – a .
Cette expression est la vitesse moyenne du mobile sur l'intervalle de temps [a ; b], c'est-à-dire la vitesse constante
qu'il faudrait donner au mobile pour qu'il parcourt la même distance dans la même durée.
2. On appelle intensité efficace I d'un courant alternatif, l'intensité d'un courant continu qui produirait à travers une
résistance le même effet Joule pendant la durée d'une période.
Si l'intensité du courant alternatif à l'instant t est donnée par I =
I
ˆ
sin t, la loi de Joule conduit à :
W(T) = R I 2 T =
dt)t(IR
T
0
2
, d'où I 2 = 1
T
T
0
2dt)t(I
c'est-à-dire que I 2 est la valeur moyenne sur [0 ; T] de la fonction t
Error!
I 2(t).
 La valeur moyenne est égale à une valeur de la fonction continue f.
Il existe un réel c de l'intervalle [a ; b] tel que : f(c) =
b
adt)t(
ab 1f
.
V- Applications du calcul intégral
1- On considère la fonction f définie sur l'intervalle [0 ; 45] par x
Error!
100 – 80 e – 0,02 x.
On note C la courbe représentative de la fonction f dans un repère orthogonal.
1. Déterminer la dérivée f ' de la fonction f.

2. Étudier le signe de la dérivée et dresser le tableau de variation de la fonction f.
3. On considère l'intégrale I =
45
0
x02,0 dx)e80100(
qui représente l'aire du domaine
délimité par la courbe C, l'axe des abscisses et les droites d'équation x = 0 et x = 45.
a) Montrer que I = 500 + 4000 e – 0,9.
b) En déduire la valeur arrondie de I au dixième d'unité d'aire.
1
2- Aire d'un triangle
2
On considère les points A(3 ; 2) et B(5 ; 0) dans un repère orthogonal (O;
Error!
,
Error!
) d'unité
1 cm.
1. Donner une équation des droites (OA) et (AB).
2. En utilisant le calcul intégral, calculer en cm 2 l'aire du triangle OAB.
3. Vérifier le résultat en appliquant la formule donnant l'aire d'un triangle.
4. Déduire de la question 2. la valeur moyenne de f sur l'intervalle [0 ; 5].
3- Statique
3
Une poutre de 8 mètres et de poids linéique 400 N.m – 1 repose par ses extrémités A et B sur
des supports dans un même plan horizontal.
Outre son poids, la poutre supporte une charge dont la répartition est :
C(x) = 500 x pour 0 x 4 et C(x) = 4000 – 500 x pour 4 x 8.
C(x) est la charge exercée au point d'abscisse x et exprimée en N.m – 1.
a) Représenter la fonction de répartition de charge linéaire totale Q (c'est-à-dire la charge C(x)
plus le poids).
b) Calculer les actions aux appuis.
4- Intensité moyenne
4
Un circuit est parcouru par un courant alternatif sinusoïdal d'intensité instantanée i.
i(t) =
I
ˆ
sin t avec
I
ˆ
: intensité maximale
1. Calculer l'intensité moyenne
I
sur une période, puis sur une alternance
I
1 (une demi période).
2. Déterminer l'intensité moyenne
I
2 du courant redressé monoalternance.
3. Déterminer l'intensité moyenne
I
3 du courant redressé double alternance.
1
1. f '(x) = 1,6 e – 0,02 x 2. fonction croissante (0; 20) (45 ; 67,5) 3. I = 662,6 unités d'aire
2
1. y = 2
3x y = – x + 5 2. A = 5 cm 2 3. idem 4.
f
= 1
3
1. Courbe symétrique/x = 4 2. RA = RB = 5600 N

PhG - Calcul intégral
4
1.
I
= 0
I
1 = 2
I
ˆ
2.
I
2 =
I
ˆ
3.
I
3 = 2
I
ˆ