Intégrale

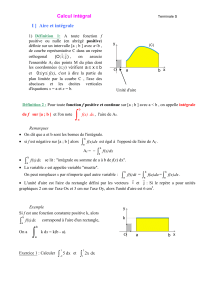
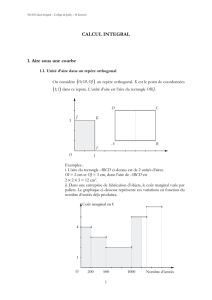
Chapter 1
Primitives et Intégrales
1
Part I
Primitives
2
Part II
Intégration
3
1.1
Notion d’intégrale d’une fonction
! ! ! !
! !
Le plan étant muni d’un repère orthogonal O; i ; j , on dé…nit les points I, J et K par OI = i ; OJ = j
, = et OIKJ est un rectangle. L’aire du rectangle OIKJ dé…nit alors l’unité d’aire (u.a.).
1.1.1 Aire et intégrale d’une fonction positive
1.1.1.1 Dé…nition
Soit f une fonction continue et positive sur un intervalle [a; b] et C sa courbe représentative dans le repère
Z b
! !
O; i ; j : L’intégrale de a à b de f est le réel noté
f (x)dx , égal à l’aire, exprimée en unités d’aire, du
a
domaine D délimité par C, l’axe des abscisses et les droites d’équations x = a et x = b.
Remarque a et b sont les bornes de l’intégrale et x est une variable muette : elle n’intervient pas dans le
Z b
Z b
Z b
f (u)du:
f (t)dt =
résultat. On peut la remplacer par les lettres t ou u, ainsi :
f (x)dx =
a
a
a
Z 0
Z 3
Exemples : a)
3dx = 6: b)
xdx = 2 (3+1)
= 4:
2
2
1
1.1.2 Valeur moyenne
1.1.2.1 Dé…nition
Soit f une fonction continue et positive sur un intervalle [a; b] avec a < b. La valeur moyenne de f sur [a; b]
Z b
1
est le réel = b a f (x)dx:
a
Z b
Z b
1
Remarque : = b a f (x)dx () (b a) =
f (x)dx:
a
a
Donc la valeur moyenne de f sur [a; b] est donc le réel tel que le rectangle de dimensions et b a soit de
même aire que le domaine D délimité par la courbe représentant f , l’axe des abscisses et les droites d’équations
x = a et x = b:
4
1.2
Intégrale et primitive
1.2.1 Intégrale d’une fonction continue, positive et croissante sur un intervalle [a; b]
1.2.1.1 Théorème
Soit f une fonction continue, positive et croissante sur un intervalle I = [a; b] . On note C, sa courbe
représentative dans le plan muni d’un repèreZ orthogonal.
x
On dé…nit sur [a; b] la fonction A : x 7 !
f (t)dt et on …xe xo dans [a; b] .
a
Cette fonction A est dérivable sur I et sa dérivée est f:
Preuve
On …xe xo dans [a; b]: L’aire de la surface coloriée est A (xo ) : (…gure 4).
On a hf (xo ) A(xo + h) A(xo ) hf (xo + h), puisque f est croissante sur I:
Selon que h > 0 ou h < 0 , on a :
f (xo ) A(xo +h)h A(xo ) f (xo + h) ou f (xo + h) A(xo +h)h A(xo ) f (xo ):
Comme f est continue sur I, donc lim f (xo + h) = f (xo ) , et d’après le théorème des gendarmes, il en résulte
h!0
A(xo +h) A(xo )
h
h!0
lim
= f (xo ):
Donc A est dérivable en a et A0 (xo ) = f (xo ); pour tout xo 2 I.
1.2.2 Primitive d’une fonction continue
1.2.2.1 Théorème admis
Soit f une fonction continue sur un intervalle [a; b]: Alors la fonction
dé…nie sur [a ; b] par (x) =
Z
est l’unique primitive de f sur [a; b] qui s’annule en a:
Remarques
La fonction , dé…nie dans le théorème, est donc dérivable sur [a; b] , de dérivée f:
Ce résultat montre que toute fonction continue sur [a; b] admet une, donc des primitives sur [a; b]:
Plus généralement, toute fonction continue sur un intervalle I quelconque admet des primitives.
Z b
f (t)dt = F (b) F (a):
Soit F une primitive quelconque de f sur [a; b], alors
x
f (t)dt
a
a
En e¤et, il existe une constante k telle que pour tout x de [a; b], F (x) = (x) + k. Alors :
Z b
f (t)dt puisque (a) = 0.
F (b) F (a) = (b) + k
(a) k = (b)
(a) = (b) =
a
1.2.3 Généralisation de l’intégrale à l’aide d’une primitive
1.2.3.1 Propriété et dé…nition
Soit f une fonction continue sur un intervalle I et F une primitive quelconque de f sur I. Pour tous réels a
et b de I, la di¤érence F (b) F (a) ne dépend pas de la primitive de f choisie.
Z b
On dé…nit alors l’intégrale de a à b de f par
f (t)dt = F (b) F (a):
a
Z b
On écrit aussi :
f (t)dt = [F (x)]ba = F (b) F (a) :
a
Exemple
Z 1
h 2
(x x3 ) dx = x2
2
x4
4
i1
=
2
12
2
1.3
1.3.1
1ère propriété
( 2)2
2
14
4
( 2)4
4
: = ::: = 49 :
Propriétés de l’intégrale
Z
a
f (t)dt = 0
a
5
1.3.2 Relation de Chasles
Soit f une fonction continue sur un intervalle I. Pour tous réels a, b et c de I, on a :
Z
b
f (t)dt +
a
:
Preuve
Z
Z
b
Z
c
f (t)dt =
b
Z
c
f (t)dt
a
c
f (t)dt +
f (t)dt = F (b) F (a) + F (c)
a
b
Z a
Z b
f (t)dt =
f (t)dt:
Conséquence :
a
F (b) = F (c)
F (a) =
Z
c
f (t)dt:
a
b
1.3.3 Linéarité
Soit f et g deux fonctions continues sur un intervalle I et k un réel. Pour tous réels a et b de I, on a :
Z b
Z b
Z b
Z b
Z b
(f + g) (t)dt =
f (t)dt +
g(t)dt et
(kf ) (t)dt = k f (t)dt
a
a
a
a
a
Preuve : Si F et G sont des primitives de f et g sur I, alors F + G est une primitive de f + g, et kF une
primitive de kf sur I: etc::::
1.3.4 Intégrales et inégalités
Soit f une fonction dé…nie et continue sur unZintervalle I de R, et a, b deux réels appartenant à I.
b
i) Si a b et f 0 sur l’intervalle I, alors
f (t)dt 0:
Za b
ii) Si a b et f 0 sur l’intervalle I, alors
f (t)dt 0:
a
Z b
f (t)dt 0:
iii) Si a b et f 0 sur l’intervalle I, alors
a
Z b
iv) Si a b et f 0 sur l’intervalle I, alors
f (t)dt 0:
a
1.3.5 Conservation de l’ordre
Soit f et g deux fonctions continues sur [a; b]. Si f
Z b
Z b
f (x) g(x) , alors
f (x)dx
g(x)dx:
a
g sur [a; b], c’est-à-dire si, pour tout réel x de [a; b],
a
Preuve : Si f
g sur [a; b] , alors, pour tout réel x de [a; b] , g(x)
continue sur [a; b]:
Z b
D’après la propriété de positivité, on obtient
(g(x) f (x)) dx
a
Z b
Z b
Z b
f (x)dx 0: Donc
g(x)dx
f (x)dx:
a
a
f (x)
0 . D’autre part, g
0: Puis par linéarité :
Z
f est
b
g(x)dx
a
a
1.3.6 Inégalités de la moyenne
Soit f une fonction continue sur un intervalle I, et a et b deux réels de I.
i) Si a
b et s’il existe deux réels m et M tels que m
f (x)
M , pour tout réel x de [a; b] , alors
Z b
m(b a)
f (x)dx M (b a):
a
Z b
ii) S’il existe un réel M positif tel que jf j M sur I, alors
f (x)dx
M jb aj:
a
Preuve : i) Pour tout réel x de [a; b] , on a : m
Z b
Z b
Z b
mdx
f (x)dx
M dx; c’est à dire m(b
a
a
a
ii) Il su¢ t de prendre m =
M , dans i).
f (x)
a)
Z
M , donc, par conservation de l’ordre, on obtient :
b
f (x)dx
M (b
a):
a
6
1.4
Intégrale d’une fonction continue et négative sur [ a , b ]
f est une fonction continue et négative sur [a; b] . C est sa courbe représentative dans un repère orthogonal.
D est le domaine compris entre C , l’axe des abscisses et les droites d’équations x = a et x = b .
Dans ce cas,
Z on convient que l’intégrale de a à b de f est l’opposée de l’aire de D:
b
On note :
f (x)dx = aire de D:
Z b
On dit parfois que
f (x)dx est l’aire algébrique du domaine compris entre C , l’axe des abscisses et les
a
a
droites d’équations x = a et x = b pour indiquer qu’elle est positive si f est positive sur [a; b], négative si f
est négative sur [a; b].
1.5
Intégrale d’une fonction continue de signe quelconque sur [a ; b]
Pour une fonction continue et de signe quelconque sur [a; b] , on convient que l’intégrale de a à b de f est
la somme des aires algébriques des domaines dé…nis à partir des intervalles sur lesquels f (x) garde un signe
constant.
Exemple :
f est la fonction dé…nie sur [a; b] par la courbe ci-contre.
Z b
f (x)dx = aire de (D1 ) aire de (D2 ) + aire de (D3 ) aire de (D4 ):
a
1.6
Aire d’un domaine compris entre deux courbes
Soit f et g deux fonctions continues sur un intervalle I, a et b deux réels de I tels que a b.
Lorsque f
g sur [a; b] , l’aire en u.a. du domaine limité par les courbes Cf et Cg sur [a; b] (en bleuté sur
Z b
(g(x) f (x)) dx:
la …gure) est calculée par : aire de (D) =
a
Le domaine D peut être décrit, si besoin est, comme l’ensemble des points M (x; y) tels que : a
f (x) y g(x):
1.7
x
b et
Intégration par parties
1.7.1 Propriété
Soit u et v deux fonctions dérivables sur l’intervalle I telles que u0 et v 0 soient continues sur I. Pour tous réels
a et b de I, on a :
Z
b
0
u (x)v(x)dx =
a
Z
a
b
[u(x)v(x)]ba
u(x)v 0 (x)dx = [u(x)v(x)]ba
Z
1
u(x)v 0 (x)dx
a
Z
b
u0 (x)v(x)dx
a
Exemples
Z 1
Z 1
x
x 1
xe dx = [xe ]0
ex dx = (e 0) [ex ]10 = e (e 1) = 1:
0Z
Z0 e
Z e
e
e
1
ln xdx = [x ln x]1
x x dx = (e ln e 1 ln 1)
dx = e
1
b
1
0
(e
1) = 1:
1
7
8
9