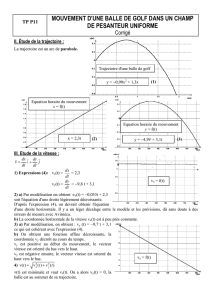
Chapitre 5 ‐ Trigonométrie, deuxième partie

!
Chapitre!5!‐!Trigonométrie,!deuxième!partie!!
Expression exacte de nombres trigonométriques
Exercices
1) L'exercice 16 du chapitre 4 était consacré au triangle d'or. En utilisant les résultats et
les constructions qui apparaissent dans sa résolution, établir l'expression exacte de
a)
€
sin π
10
et
€
cos π
10
; b)
€
cos π
5
et
€
sin π
5
.
2) En étudiant les propriétés du triangle isocèle rectangle, établir l'expression exacte de
€
cos π
4
,
€
sin π
4
et
€
tan π
4
.
3) Etudier les propriétés du triangle équilatéral de manière à établir l'expression exacte de
a)
€
cos π
3
,
€
sin π
3
et
€
tan π
3
; b)
€
sin π
6
,
€
cos π
6
et
€
tan π
6
.
4) En revenant aux définitions de cosα, sinα et tanα, établir l'expression exacte de
a)
€
cos0
,
€
sin0
et
€
tan0
; b)
€
cos π
2
,
€
sin π
2
et
€
tan π
2
.
5) En utilisant les propriétés obtenues dans la résolution des exercices précédents, compléter
le graphique et le tableau qui se trouvent à la page suivante. Il y a deux colonnes pour α :
l'une doit contenir les valeurs 0°, 30°, 45°, 60° et 90°, l'autre leur équivalent en radians.
1"

2"
α
cosα
sinα
tanα

Corrigé des exercices
1) Reprenons la construction faite dans la résolution de l'exercice 16)
du chapitre 4 et ajoutons-y deux points :
E = milieu de [AB]
F = milieu de [BC]
Rappelons que
€
d(A, B) =d(A, C) =L
d(B, C) =
avec L
=1+5 2
Le triangle isocèle ABC peut être découpé en deux triangles rectangles AFC et AFB.
Considérons le triangle AFC et nommons α1, ϕ et γ les amplitudes de ses angles et a1,
f et c1 les longueurs de ses côtés, comme indiqué sur le dessin.
€
ϕ=π
2
car AFC est rectangle en F
€
α1=α
2=1 2
π
5=π 10
€
a1=d(C, F) =d(B, C)
2= 2
;
€
f=d(A, C) =L
.
€
sin π
10 =sinα1=a1 f=
2
L=1 2 L=1 2
2
1+5=1 1+5=1 5+1=5−1
5+1
( )
5−1
( )
=5−1
5−1=5−1 4
Le triangle isocèle ABD peut être découpé en deux triangles rectangles AED et BED.
Considérons le triangle AED et nommons α, ε et δ3 les amplitudes de ses angles et a2,
e et d les longueurs de ses côtés, comme indiqué sur le dessin.
€
ε=π
2
car AED est rectangle en E
€
α=π
5
par définition de ABC
€
d=d(A, E) =d(A, B)
2=L 2
€
e=d(A, D) =d(B, D) =d(B, C) =
(voir ex. 16) du chapitre 4)
€
cos π
5=cosα=d e=
L
2
=1 2
L
=1 2
1+5
2=1+5 4
3"

Nous avons obtenu que
€
sin π
10 =5−1 4
et que
€
cos π
5=1+5 4
.
Pour trouver
€
cos π
10
et
€
sin π
5
, appliquons la relation fondamentale :
€
cos2α+sin2α=1
€
cos2π
10 +sin2π 10 =1
€
cos2π
5+sin2π 5=1
€
cos2π
10 =1−sin2π 10
€
sin2π
5=1−cos2π 5
€
cos2π
10 =1−5−1 4
2
€
sin2π
5=1−1+5 4
2
€
42cos2π
10 =42−5−1
( )
2
€
42sin2π
5=42−1+5
( )
2
€
4 cos π
10
2
=16 −5−2 5 +1
( )
€
4 sin π
5
2
=16 −1+2 5 +5
( )
€
4 cos π
10
2
=16 −5+2 5 −1
€
4 sin π
5
2
=16 −1−2 5 −5
€
4 cos π
10
2
=10 +2 5
€
4 sin π
5
2
=10 −2 5
€
4 cos π
10 = ± 10 +2 5
€
4 sin π
5= ± 10 −2 5
Comme
€
π
10
est du 1er quadrant, Comme
€
π
5
est du 1er quadrant,
€
4 cos π
10 =10 +2 5
€
4 sin π
5=10 −2 5
€
cos π
10 =10 +2 5 4
€
sin π
5=10 −2 5 4
Conclusion
a)
€
sin π
10 =5−1 4
et
€
cos π
10 =10 +2 5 4
.
b)
€
cos π
5=1+5 4
et
€
sin π
5=10 −2 5 4
.
4"

2) ABC étant rectangle,
€
b2=a2+c2
€
b=a2+c2
.
ABC étant isocèle,
c = a.
ABC étant isocèle rectangle,
€
b=a2+c2=a2+a2=2a2=2a
.
€
α=γ=π
4
€
β=π
2
€
cos π
4=cosα=c b=a
2 a=1 2=2
2
€
sin π
4=sinα=a b=a
2 a=1 2=2
2
€
tan π
4=tanα=a c=a a=1
5"