Trigonométrie

Chapitre. Trigonométrie
Rappel de vocabulaire:
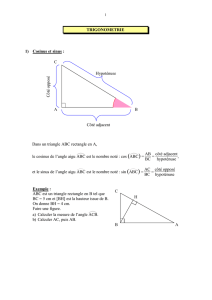
ABC est un triangle rectangle en A.
[BC] est l'hypoténuse.
[AB] est le côté adjacent à l'angle d B .
[AC] est le côté opposé à l'angle d B .
[AC] est le côté adjacent à l'angle d C .
[AB] est le côté opposé à l'angle d C
I. Cosinus, sinus, tangente d’un angle aigu
Soit BAC un triangle rectangle en A, on définit
• le cosinus de l’angle
d
dd
d
B , noté cos
d
dd
d
B le rapport AB
BC ;
• le sinus de l’angle
d
dd
d
B , noté sin
d
dd
d
B le rapport AC
BC ;
• la tangente de l’angle
d
dd
d
B notée tan
d
dd
d
B , le rapport AC
AB
remarque 1: cos
d
B = longueur du côté adjacent à
d
B
longueur de l’hypoténuse
sin
d
B = longueur du côté opposé à
d
B
longueur de l’hypoténuse tan
d
B = longueur du côté opposé à
d
B
longueur du côté adjacent à
d
B
remarque 2: Le cosinus et le sinus d’un angle aigu sont compris entre 0 et 1.
La tangente d’un angle aigu est un nombre positif.
II. Deux formules fondamentales
tan x = sin x
cos x
démonstration : sin x
cos = AC BC × BC AB
sin x
cos = AC AB
sin x
cos = tan x .
cos
2
x + sin
2
x = 1
démonstration : cos
2
x + sin
2
x = ( AB
BC )
2
+ ( AC
BC )
2
cos
2
x + sin
2
x = AB
2
BC
2
+ AC
2
BC
2
cos
2
x + sin
2
x = AB
2
+ AC
2
BC
2
,
par le théorème de Pythagore, AB
2
+ AC
2
= BC
2
donc cos
2
x + sin
2
x = 1
remarque 1: Application au quart de cercle de rayon 1 :
Dans un repère orthonormé (O, I, J), un point M du premier quart de cercle de centre O de rayon 1 a pour coordonnées:
M (cos x, sin x ) où x est une mesure de l’angle
a
PON.
démonstration:
M a pour coordonnées (OP; OR) dans ce repère.
cos x = OP
OM Donc cos x = OP 1 cos x = OP
OR = MP, donc sin x = MP
OM sin x = OR 1 sin x = OR
De plus: tan x = IN
OI donc tan x = IN
1 tan x = IN
Quelques valeurs trigonométriques à connaître:
B
A C
hypoténuse
J
sin
x
cos
x
1
O
N
I
1
M
R
P

III. Et dans les exercices
Voici quelques petits trucs pour faire plus facilement les exercices
1) On cherche à connaître un angle.
Enoncé de l'exercice:
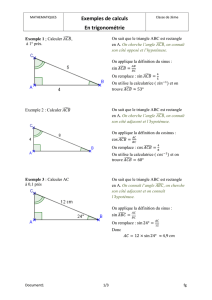
ABC est un triangle rectangle en A avec AB = 13 cm et AC = 8 cm.
Déterminer une valeur arrondie au degré de
a
ABC.
Procédure:
1) On vérifie que cet angle est un angle de triangle rectangle:
on écrit: "Le triangle
Le triangleLe triangle
Le triangle ABC est rectangle en
est rectangle enest rectangle en
est rectangle en A".
2) On regarde si on connaît :
• l'hypoténuse et le côté adjacent de l'angle On va utiliser le cosinus de l'angle.
• l'hypoténuse et le côté opposé à cet angle On va utiliser le sinus de l'angle.
• le côté opposé et le côté adjacent à l'angle On va utiliser la tangente de l'angle.
3) On écrit la formule qui nous intéresse: ici, on connaît le côté opposé et le côté adjacent à l'angle. On
va donc utiliser la tangente de l'angle.
On écrit: "tan a
aa
a
ABC = AC
AB"
"tan a
aa
a
ABC = 8
13"
5) On a maintenant besoin de la calculatrice pour trouver une valeur approchée de l'angle:
Sur la plupart des calculatrices récentes, on tape la procédure suivante:
sur Casio fx-92 CollègeII: I0G JOWXZKa
écriture à l'écran: tan
-1
( 8 ÷ 1 3 )
Sur Texas Instruments TI Collège &` M @ F H:D
écriture à l'écran: tan
-1
( 8 ÷ 1 3 )
La calculatrice va écrire le résultat suivant: 31.60750225
C'est une valeur arrondie de l'angle.
On va donc noter sur la copie: " a
aa
a
ABC %
%%
% 32 °".
Au bilan, voilà ce qui apparaît sur la copie:
Le triangle ABC est rectangle en A.
donc tan a ABC = AC
AB tan a
ABC = 8
13 donc a
ABC % 32 °

2) On cherche une longueur.
Enoncé de l'exercice:
On considère un triangle ABC rectangle en A, tel que AB = 5 cm et
a
ACB
= 40 °.
Déterminer une valeur arrondie au dixième de BC.
Procédure:
1) On vérifie que cet angle est un angle de triangle rectangle:
on écrit: "Le triangle
Le triangleLe triangle
Le triangle ABC es
eses
est rectangle en
t rectangle ent rectangle en
t rectangle en A".
2) On regarde si on connaît :
• l'hypoténuse et le côté adjacent de l'angle On va utiliser le cosinus de l'angle.
• l'hypoténuse et le côté opposé à cet angle On va utiliser le sinus de l'angle.
• le côté opposé et le côté adjacent à l'angle On va utiliser la tangente de l'angle.
3) On écrit la formule qui nous intéresse: ici, on connaît l'hypoténuse et le côté à l'angle. On va donc
utiliser le sinus de l'angle.
On écrit: " sin a
aa
a
ACB = AB
BC "
Ce qui nous intéresse, c'est de déterminer la longueur BC. Faut-il multiplier ? diviser ?
Pour être sûr de ne pas se tromper, on va transformer cette écrire pour faire apparaître un produit en
croix.
on écrit: " sin a
aa
a
ACB
1 = AB BC"
La division par 1 ne change pas la valeur du premier membre.
Ici, on obtient donc
on écrit: "BC = AB × 1
sin a
aa
a
ACB"
"BC = 5 × 1
sin 40 "
La calculatrice donne sur son écran: 7.778619134
On écrit: "BC %
%%
% 7,8 cm"
Au bilan, voilà ce qui apparaît sur la copie:
Le triangle ABC est rectangle en A.
sin a ACB = AB
BC soit sin a
ACB
1 = AB BC
BC = AB × 1
sin a ACB
BC = 5 × 1
sin 40 cm
BC % 7,8 cm

Il est évident que pour faire ces exercices, il faut connaître par cœur les relations:
remarque 1: cos
d
B = longueur du côté adjacent à
d
B
longueur de l’hypoténuse
sin
d
B = longueur du côté opposé à
d
B
longueur de l’hypoténuse
tan
d
B = longueur du côté opposé à
d
B
longueur du côté adjacent à
d
B
IV. Quelques valeurs remarquables à connaître
mesure de
l'angle en
degrés 30 45 60
cosinus 3
2 2
2 ou 12 1
2
sinus 1
2 2
2 ou 12 3
2
tangente 3
3 ou 13 1 3