Leçon 7 La dérivation

Leçon 7
La dérivation
Un petit exemple pour bien préciser les choses :
Prenons la fonction f(x) = x
2
pour x∈[0 ; 4]. Nous allons nous intéresser à la vitesse de la
fonction, nous connaissons la formule de physique donnant la vitesse moyenne d’un mobile :
t
d
V=
Entre les valeurs x = 1 et x = 3, cela donne :
V
moy
= 4
2
19
1
3
)1(f)3(f =
−
=
−
−
. Nous utilisons ici ce qu’on appelle en mathématiques le taux
d’accroissement T calculé entre 1 et 3, il représente le coefficient directeur de la droite (AB)
(
AB
AB xx yy
a−
−
= vu en seconde).
La vitesse moyenne ne dit pas ce qui se passe à chaque moment du trajet effectué. Aussi, nous
allons chercher une vitesse instantanée permettant de décrire les variations en chaque point.
Si nous voulons la vitesse au point A, l’idée est de se rapprocher du point A en prenant
x =1+h h petit et en calculant le taux d’accroissement entre les deux points A’ d’abscisse
1+h et le point A d’abscisse 1 (h est un réel positif ou négatif petit, pensons à 0.1 ou à − 0,1
par exemple) :
V = h2
hhh2 h1hh21 h1)h1( 1)h1( )1(f)h1(f
2222
+=
+
=
−++
=
−+
=
−+ −+ (h ≠ 0)
Si nous voulons l’équation de la sécante (AB) :
y = ax + b
nous connaissons a = 4.
Nous pouvons utiliser le point A(1 ; 1)
1 = 4(1) + b, cela donne b = −3.
(AB) y = 4x −
−−
− 3 .
Le taux d’accroissement ne donne pas de
renseignements sur ce qui se passe entre les
deux points A et B. Si nous prenons C (−1 ; 1)
à la place de A
, le taux d’accroissement
n’indiquera pas qu’entre −
1 et 0 la fonction est
décroissante puis croissante.

Si nous faisons tendre h vers 0, alors nous aurons la vitesse instantanée de la fonction en A
c’est-à-dire pour x = 1 (cela revient à regarder le compteur de vitesse de la voiture à un
moment donné) :
lim 2 + h = 2 2 s’appelle le nombre dérivé de f pour x = 1
h  0
Si nous généralisons, le nombre dérivé de f en chaque point x
0
sera :
)x('f
h)x(f)hx(f
lim
0
00
=
==
=
−
−−
−
+
++
+
par définition, f ’(x
0
) s’appelle le
h 0 nombre dérivé de f en x
0
.
Pour la fonction étudiée ici, nous obtenons :
h
hhx2
lim
h
xhhx2x
lim
h
x)hx(
lim
2
0
2
0
2
0
2
0
2
0
2
0
+
=
−++
=
−+
h0 h0 h0
00
x2hx2lim =+=
x0
Conséquence, en x = 1, la vitesse instantanée de f est 2, on écrit f ’(1) = 2.
en x = 3, la vitesse instantanée de f est 6, on écrit f ’(3) = 6.
mais en x = −1, la vitesse sera − 2 et donc f ’(– 1) = – 2 .
Nous pouvons dire maintenant, à tout moment, si cette fonction sera croissante ou
décroissante.
La fonction dérivée de f(x) = x
2
sera donc f ’(x) = 2x ∀
∀∀
∀ x∈
∈∈
∈R.
Cette fonction ayant le même signe que le taux d’accroissement permettra donc de savoir si la
fonction est croissante ou décroissante et donc de construire son tableau de variations.
Théorème
Soit une fonction f, définie sur un intervalle I et dérivable sur cet intervalle :
Si pour tout x ∈ I, f ‘(x) > 0 , alors sera strictement croissante sur I.
Si pour tout x ∈ I, f ‘(x) < 0, alors f sera strictement décroissante sur I.
Si pour tout x ∈ I, f ‘(x) = 0, alors f sera constante sur I.
Nous avons aussi le théorème de la tangente très utilisé :
Théorème
Soit une fonction f, définie sur un intervalle I et dérivable sur cet intervalle, alors en tout
point de la courbe d’abscisse x
0
, nous avons une tangente dont l’équation sera :
y = f ’(x
0
) (x −
−−
− x
0
) + f (x
0
) (T
X0
)
Remarque : cette tangente est la position limite de la sécante (AB) (voir figure) lorsque B tend
vers A. Son coefficient directeur est le nombre dérivé de f en x
0
.
En terminale, nous l’utiliserons comme meilleure approximation affine de la fonction f au
voisinage de x
0
:
Par exemple, pour la fonction f(x) = x
2
, la meilleure approximation affine de f au voisinage de
1 sera : f ‘(1)(x − 1) + f(1) = 2(x − 1) + 1 = 2x − 1 et nous pouvons écrire :

Si x est voisin de 1 alors : f(x ) ≈ 2x − 1
Vérification : x = 1,04 nous avons (1,04)
2
= 1,0816 et 2x − 1 donne 2(1,04) − 1 = 1,08).
Il reste maintenant à utiliser les théorèmes de la dérivation.
Vous devez connaître les théorèmes suivants :
Si f(x) = ax + b alors f ’(x) = a, pour tout x réel.
Si f(x) = ax
2
+ bx + c alors f ’(x) = 2ax + b, pour tout x réel.
Et j’ajoute aussi :
Si f(x) =
x
1
, x ≠ 0, alors f ’(x) =
2
x
1
−, x ≠ 0.
Si f(x) = ku(x), avec k réel, alors f ’(x) = ku ’(x).
Si f(x) =
)x(u 1, avec u(x)
≠ 0 alors f ’(x) = 2
)]x(u[
)x('u
− avec u(x) ≠ 0.

Lycée Première STG
Elève :
Classe :
Fiche n°18
La dérivation
Exercice 1
Donner la fonction dérivée des fonctions suivantes : x∈R
f(x) =
3
x45
−
; f(x) = 3x
2
− 5x + 7 ;
f(x) = (2x − 3)
2
; f(x) =
x
2 ;
f(x) =
x
4
5
−.
Exercice 2
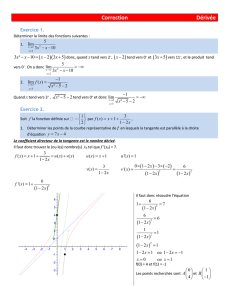
Soit la fonction f définie par f(x) = −x
2
+ 6x + 3, x∈R.
a) Calculer f ‘(x).
b) Etudier les variations de f quand x varie dans R.
c) Donner une équation de la tangente à la courbe pour x = 1 puis x = 3.
d) Représenter graphiquement la courbe et les deux tangentes.
e) Chercher s’il existe une valeur de x, x
0
telle que la tangente à la courbe représentant f soit
perpendiculaire à la tangente en x = 1.
Exercice 3
Soit g(x) =
2
x
1avec x un réel quelconque.
a) Etudier les variations de g et tracer la courbe.
b) Donner deux caractéristiques de cette fonction.
c) Donner une équation de la tangente (T
1
) à la courbe au point d’abscisse x = 1.
(Ces problèmes sont assez théoriques, nous verrons au chapitre suivant les applications en
économie)

Correction
Fiche 18
Exercice 1
La première fonction f(x) =
3
x45
−
est une fonction affine qui peut s’écrire f(x) = x
3
4
3
5−et
donc f ’(x) = 3
4
−
−−
−, Df = Df ’ = R .
La deuxième fonction est une fonction polynôme de degré 2 (Trinôme du second degré).
f(x) = 3x
2
– 5x + 7, f ’(x) = 6x −
−−
− 5 pour tout x appartenant à R. Df = Df ’ = R.
f(x) = (2x − 3)
2
, pour dériver, nous devons ici développer.
f(x) = 4x
2
− 12x + 9 et donc f ’(x) = 8x −
−−
− 12 . Df =Df ’ = R .
f(x) =
x
2, il faut poser x
≠ 0. f ’(x) = 2
−2
x
1=
2
x
2
−
−−
− avec x ≠ 0. Df = Df ’ = R
*
.
f(x) =
x
4
5
−, il faut poser ici x ≠ 4. Nous allons dériver cette fonction qui est de la forme
k
)x(u1. u(x) = 4 − x et donc u ’(x) = − 1.
f ’(x) = 5 
−
−
−
2
)x4( 1=
2
)x4( 5 −
−−
−
avec x ∈
∈∈
∈ R \{4} c’est-à-dire x ≠
≠≠
≠ 4 .
Exercice 2
f(x) = −x
2
+ 6x +3, x∈R. (polynôme de degré 2)
a) f ’(x) = −2x + 6 pour tout x réel.
b) Le signe de f ’ nous donnera les variations de f.
Nous pouvons faire un seul tableau contenant l’étude du signe de f ’ et les variations de f.
x −∞ 3 +∞
(Théorème sur le
−2x + 6 + 0 − signe de ax +b )
12
f(x) f(3) = 12.
−∞ −∞
Nous allons admettre que la fonction tend vers −∞ quand x devient très grand ou très petit
(x tend vers +∞ ou −∞, c’est – x
2
qui donne la réponse).
La fonction étudiée est donc croissante pour x ∈
∈∈
∈ ] −
−−
−∞
∞∞
∞ ; 3] et décroissante sur l’intervalle
[3 ; + ∞
∞∞
∞ [ , nous reconnaissons une parabole tournée vers les y négatifs à cause de a < 0,
a = − 1 devant x
2
.
c) Pour x = 1, appelons la tangente (T
1
). Son équation sera :