Fiche de cours

Chapitre 9
Terminale S
Les nombres complexes - 2
Ce que dit le programme :
CONTENUS
CAPACITÉS ATTENDUES
COMMENTAIRES
1ère partie
Forme algébrique, conjugué.
Somme, produit, quotient.
Équation du second degré à
coefficients réels.
• Effectuer des calculs algébriques avec
des nombres complexes.
• Résoudre dans C une équation du second
degré à coefficients réels.
• Représenter un nombre complexe par un
point ou un vecteur.
• Déterminer l’affixe d’un point ou d’un
vecteur.
On introduit dans ce chapitre des éléments
lui donnant une dimension historique.
Le plan est muni d’un repère orthonormé
• Passer de la forme algébrique à la
forme trigonométrique et inversement.
• Connaître et utiliser la relation
La notation exponentielle est introduite après
avoir montré que la fonction θ a cosθ + i sinθ
vérifie la même relation fonctionnelle que la
fonction exponentielle.
Les nombres complexes permettent de
mémoriser les formules trigonométriques
d’addition et de duplication vues en première.
[SI] Analyse fréquentielle d’un système.
Représentation géométrique.
Affixe d’un point, d’un vecteur.

2ème partie
Forme trigonométrique :
- module et argument,
interprétation géométrique dans
un repère orthonormé direct ;
- notation exponentielle.
(O ; ⃗u ; ⃗v ).
2
z z=∣z∣
• Effectuer des opérations sur les
nombres complexes écrits sous
différentes formes.
I. Forme trigonométrique
1.1) Forme trigonométrique d'un nombre complexe
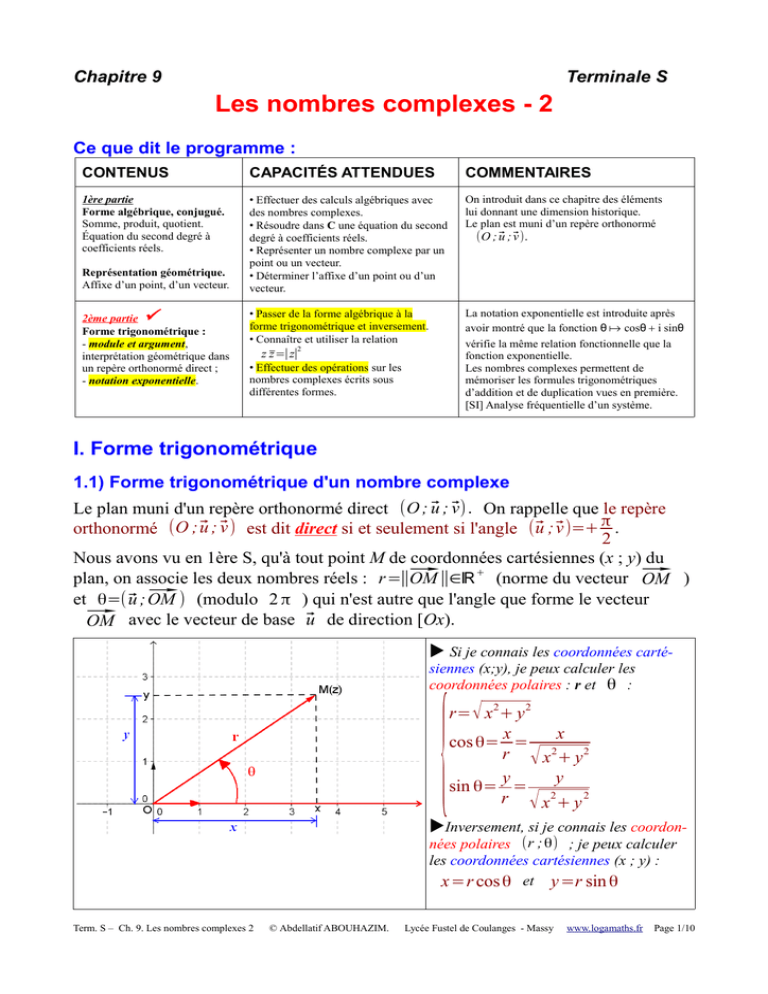
Le plan muni d'un repère orthonormé direct (O ; ⃗u ; ⃗v ). On rappelle que le repère
orthonormé (O ;⃗u ; ⃗v ) est dit direct si et seulement si l'angle (⃗u ;⃗v )=+ π .
2
Nous avons vu en 1ère S, qu'à tout point M de coordonnées cartésiennes (x ; y) du
plan, on associe les deux nombres réels : r=∥⃗
OM ∥∈ℝ + (norme du vecteur ⃗
OM )
et θ=( ⃗u ; ⃗
OM ) (modulo 2 π ) qui n'est autre que l'angle que forme le vecteur
⃗
OM avec le vecteur de base ⃗u de direction [Ox).
 Si je connais les coordonnées cartésiennes (x;y), je peux calculer les
coordonnées polaires : r et θ :
{
r= √ x 2+ y 2
x
x
cos θ= = 2 2
r √x +y
y
y
sin θ= = 2
r √ x + y2
Inversement, si je connais les coordonnées polaires (r ; θ) ; je peux calculer
les coordonnées cartésiennes (x ; y) :
x=r cos θ et y=r sin θ
Term. S – Ch. 9. Les nombres complexes 2
© Abdellatif ABOUHAZIM.
Lycée Fustel de Coulanges - Massy
www.logamaths.fr
Page 1/10
Le couple (r ;θ) correspond aux coordonnées polaires du point M dans le plan muni
du repère orthonormé direct (O ; ⃗u ; ⃗v ).
Nous allons – tout simplement– traduire cette écriture avec les nombres complexes.
Définition 1.
A tout point M d'affixe z, du plan complexe muni d'un repère orthonormé direct
(O ;⃗u ; ⃗v ), on associe les deux nombres réels :
r=∥⃗
OM ∥∈ℝ + qu'on appelle le module de z et on note r=∣z∣ ; et
•
θ=( ⃗u ; ⃗
OM ) (modulo 2 π ) qu'on appelle l'argument de z et on note
•
θ=arg ( z) [2π] (lire modulo 2 π , c'est-à-dire à 2 k π près).
Soit z∈ℂ et M le M d'affixe z, du plan complexe muni d'un repère orthonormé
direct (O ;⃗u ; ⃗v ). D'après cette définition, nous pouvons maintenant, réécrire la
forme algébrique de z.
z = x+iy
•
•
r=∣z∣=∥⃗
OM ∥=√ x 2+ y 2
x=r cos θ et y=r sin θ
•
x
y
• ou encore cos θ=
et sin θ=
∣z∣
∣z∣
Par conséquent : z= x+iy=r cos θ+i r sin θ = r (cos θ+i sin θ)
Définition 2.
Soit M un point du plan complexe muni d'un repère orthonormé direct (O ;⃗u ; ⃗v ).
Soit z l'affixe du point M. Alors l'écriture
z=r (cosθ+i sin θ)
s'appelle la forme trigonométrique de z, avec r=∣z∣ est le module de z et
θ=arg ( z)=( u⃗ ;⃗
OM ) (modulo 2 π ) est l'argument de z (à 2 k π près).
Exemples
Déterminer la forme trigonométrique des nombres complexes suivants :
z 1=1+i ; z 2=1+i √ 3 et z 3=−√ 3+i
Pour z 1=1+i
– 1er réflexe : Je calcule le module de z 1=1+i .
∣z 1∣= √ x 2+ y 2=√ 12+12= √ 2
– 2ème réflexe : Je calcule cos θ et sin θ :
{
x
1
2
= =√
∣z∣ √ 2 2
y
1
2
sin θ= = = √
∣z∣ √ 2 2
cos θ=
Term. S – Ch. 9. Les nombres complexes 2
© Abdellatif ABOUHAZIM.
Lycée Fustel de Coulanges - Massy
www.logamaths.fr
Page 2/10
– 3ème réflexe : Je consulte mon cercle trigonométrique :
2ème cas
1
cos θ=±
2
√3
sin θ=±
2
1er cas
cos θ=±
√2
2
√2
sin θ=±
2
3ème cas
√3
cos θ=±
2
1
sin θ=±
2
– Nous sommes bien dans le 1er cas et cos θ>0 et sin θ>0 .
π
Donc θ= 4 [ 2π] .
π
π
– Par conséquent z 1= √ 2 cos 4 +i sin 4
( ()
( ))
Pour z 2=1+i √ 3 :
– 1er réflexe : Je calcule le module de z 2=1+i √ 3
√
2
∣z 2∣=√ x + y = 1 +( √ 3) =√ 4=2
– 2ème réflexe : Je calcule cos θ et sin θ :
x 1
cos θ= =
∣z∣ 2
y √3
sin θ= =
∣z∣ 2
2
2
2
{
– 3ème réflexe : Je consulte mon cercle trigonométrique :
– Cette fois, nous sommes dans le 2ème cas et cos θ>0 et sin θ>0 .
π
Donc θ= 3 [2π] .
π
π
– Par conséquent z 2=2 cos 3 +i sin 3
Pour z 3=−√ 3+i :
– 1er réflexe : Je calcule le module de z 3=−√ 3+i
( ()
√
2
( ))
∣z 3∣= √ x + y = (−√ 3) +1 = √ 4=2
2
2
Term. S – Ch. 9. Les nombres complexes 2
2
© Abdellatif ABOUHAZIM.
Lycée Fustel de Coulanges - Massy
www.logamaths.fr
Page 3/10
– 2ème réflexe : Je calcule cos θ et sin θ :
{
x −√ 3
=
∣z∣
2
y 1
sin θ= =
∣z∣ 2
cos θ=
– 3ème réflexe : Je consulte mon cercle trigonométrique :
– Cette fois, nous sommes dans le 3ème cas et cos θ<0 et sin θ>0 .
5π
[ 2π] .
Donc θ=
6
– Par conséquent z 3=2 cos 5π +i sin 5 π
6
6
( ( ) ( ))
Cas particuliers très importants :
Soit z un nombre complexe non nul. On pose z= x+iy et arg (z)=θ [ 2π] .
Alors :
z= x−iy est le symétrique de z par rapport à l'axe des abscisses :
•
∣z∣=∣z∣ et arg (z)=−θ=−arg (z) [2π]
−z=−x−iy est le symétrique de z par rapport à l'origine O :
•
∣−z∣=∣z∣ et arg (−z)=θ+π=arg ( z)+π [ 2π]
−z=−x+iy
•
est le symétrique de z par rapport à l'axe des ordonnées :
∣−z∣=∣z∣ et arg (−z)=π−θ=π−arg (z) [2π]
1.2) Propriété des modules et arguments
Théorème 1.
Le plan complexe est muni d'un repère orthonormé direct (O ; ⃗i ; ⃗j). Soient z1 et z2
deux nombres complexes dont on connaît les formes trigonométriques telles que :
z 1=r 1 (cos θ1+i sin θ1) et z 2=r 2 (cos θ2+i sin θ2 ). Alors :
Term. S – Ch. 9. Les nombres complexes 2
© Abdellatif ABOUHAZIM.
Lycée Fustel de Coulanges - Massy
www.logamaths.fr
Page 4/10
1°) z 1 z 2=r 1 r 2 [ cos (θ1+θ2)+i sin (θ1+θ2) ]
2°)
1 1
= [ cos(−θ2)+i sin(−θ2) ] , z 2≠0
z2 r2
3°)
z1 r1
= [ cos(θ1−θ2 )+i sin (θ1−θ2) ] , z 2≠0
z2 r2
Démonstration :
z 1 z 2=r 1 ( cos θ1+isin θ1)×r 2 ( cos θ2+isin θ2 )
1°)
= r 1 r 2 [ cos θ1 cos θ2+i cos θ1 sin θ2 +i sin θ1 cos θ2−sin θ1 sin θ2 ]
= r 1 r 2 [( cos θ1 cos θ2−sin θ1 sin θ2)+i ( cos θ1 sin θ2+sin θ1 cos θ2 ) ]
z 1 z 2=r 1 r 2 [ cos (θ1+θ2)+i sin (θ1+θ2) ] = forme trigonométrique de z1z2.
d'après les formules d'addition de trigonométrie vues en 1ère S.
C'est aussi un moyen de "retrouver ces formules".
CQFD
On en déduit immédiatement que :
∣z 1 z 2∣=r 1 r 2=∣z 1∣×∣z 2∣ et arg (z 1 z 2)=θ1+θ2=arg (z 1)+arg ( z 2 ) [ 2π]
(1°)
(1°bis) ∣z 2∣=r 2=∣z∣2 et arg (z 2)=2θ=2 arg ( z ) [2π]
(1°ter) ∣z n∣=r n=∣z∣n et arg (z n)=n θ=n×arg (z) [2π] pour tout n∈ℕ
2°) On suppose que z 2≠0 , alors :
1
1
1
1
=
= ×
z 2 r 2 ( cos θ2 +i sin θ2 ) r 2 cos θ 2+i sin θ2
On multiplie par le conjugué du dénominateur, pour obtenir :
cos θ2−i sin θ2
1 1
= ×
z 2 r 2 ( cos θ2+i sin θ2)( cos θ2−i sin θ2 )
La fonction cosinus est paire et la fonction sinus est impaire, donc :
1 1 cos (−θ2 )+i sin (−θ2 )
= ×
z2 r2
cos2 θ2+sin 2 θ 2
1 1
= [ cos(−θ2)+i sin(−θ2) ] , z 2≠0
Ce qui donne :
CQFD
z2 r2
On en déduit immédiatement que, pour tout z≠0 :
1
1
1
1
=−θ2=−arg (z 2)
= =
(2°)
et arg
z2
z 2 r 2 ∣z 2∣
∣∣
( )
[2π]
3°) On suppose que z 2≠0 . En utilisant les deux résultats précédents, on a :
Term. S – Ch. 9. Les nombres complexes 2
© Abdellatif ABOUHAZIM.
Lycée Fustel de Coulanges - Massy
www.logamaths.fr
Page 5/10
z1
1
=z 1×
donc
z2
z2
∣ ∣∣ ∣ ∣ ∣
z1
1
1 ∣z ∣
= z 1× =∣ z 1∣× = 1
z2
z2
z 2 ∣z 2∣
De même, pour l'argument :
z
1
1
arg 1 =arg z 1×
=arg (z 1)+arg
=arg (z 1 )−arg (z 2)
z2
z2
z2
() ( )
( )
On en déduit immédiatement que : pour tout z 1 et z 2≠0 :
z 1 ∣z 1∣
z1
=
=arg ( z 1)−arg (z 2)
(3°)
et arg
z 2 ∣z 2∣
z2
∣∣
()
[ 2π] CQFD
[2π]
En résumé :
Il suffit de résumer les propriétés ainsi obtenues dans le théorème 1, pour les modules
d'une part et pour les arguments d'autre part, en rajoutant quelques
Pour tous nombres complexes z 1 et z 2≠0 :
(1°) ∣z 1 z 2∣=∣z 1∣×∣z 2∣
et arg (z 1 z 2)=arg (z 1 )+arg (z 2) [2π]
1
1
1
=
=−θ2=−arg (z 2) [2π]
(2°)
et arg
z 2 ∣z 2∣
z2
∣∣
(3°)
∣∣
z 1 ∣z 1∣
=
z 2 ∣z 2∣
( )
et arg
()
z1
=arg ( z 1)−arg (z 2)
z2
[2π ]
Cas particuliers très importants :
Soit z un nombre complexe non nul. On pose z = x+iy et arg (z)=θ
∣z∣=0 (ssi) z=0
4°)
5°)
z est un nombre réel positif (ssi) ∣z∣=z (ssi) z= x ∈ℝ +
(ssi) arg (z)=0 [2π]
[ 2π]
5°bis) z est un nombre réel négatif
(ssi) ∣z∣=−z (ssi) z= x∈ℝ − (ssi) arg (z)=π
6°)
[2π ]
z est un imaginaire pur à coefficient positif
π
(ssi) z=iy , y∈ℝ + (ssi) arg (z)= 2 [2π]
6°bis) z est un imaginaire pur à coefficient négatif
−π
[2π ]
(ssi) z=iy , y∈ℝ − (ssi) arg (z)= 2
Term. S – Ch. 9. Les nombres complexes 2
© Abdellatif ABOUHAZIM.
Lycée Fustel de Coulanges - Massy
www.logamaths.fr
Page 6/10
1.3) Application à la géométrie
Théorème 2.
Le plan complexe est muni d'un repère orthonormé direct (O ; ⃗i ; ⃗j). Soient A, B et
C trois points du plan d'affixes respectifs zA , zB et zC. Alors :
OA∥
OA) [2π ]
1°) ∣z A∣=OA=∥⃗
et arg (z A)=( ⃗u , ⃗
AB∥
2°) ∣z B −z A∣= AB=∥⃗
3°)
∣ ∣
z C − z A AC
=
z B − z A AB
et
arg (z B −z A)=( u⃗ , ⃗
AB)
et
arg
(
[2π ]
)
z C −z A
=(⃗
AB ,⃗
AC )
z B− z A
[2π ]
Démonstration :
1°) Immédiat, par définition.
2°) Par définition, Pour tous points A et B du plan, il existe un point M et un seul
d'affixe zM, tel que ⃗
OM =⃗
AB . Donc zM = zB – zA. Les deux égalités en découlent :
∣z B – z A∣=∣z M ∣=OM = AB et arg (z B −z A)=arg (z M )=( ⃗u ; ⃗
OM )=( ⃗u ; ⃗
AB) .
3°) D'après le théorème 1 et la propriété précédente, nous avons :
z C − z A ∣z C − z A∣ AC
=
=
– d'une part :
z B − z A ∣z B − z A∣ AB
∣ ∣
( )
– et d'autre part :
z −z
arg C A =arg (z C −z A)−arg ( z B− z A )
z B− z A
=( ⃗u ,⃗
AC )−( ⃗u ,⃗
AB)
=( u⃗ ,⃗
AC )+(⃗
AB , u⃗ )
=(⃗
AB , ⃗u )+( ⃗u , ⃗
AC )
=(⃗
AB ,⃗
AC ) d'après la relation de Chasles.
Exemple d'application :
1°) Déterminer l'ensemble E1 des points M d'affixes z dans le plan complexe
muni d'un repère orthonormé direct (O ;⃗u ; ⃗v ) vérifiant l'égalité
∣z−3+2i∣=5 (1)
2°) Déterminer l'ensemble E1 des points M d'affixes z dans le plan complexe
muni d'un repère orthonormé direct (O ;⃗u ; ⃗v ) vérifiant l'égalité
∣z−3+2i∣=∣z+1−i∣ (2)
3°) Soient A, B et C trois points d'affixes z A=3−2i , z B=−1+i et z C =6+2i
dans le plan complexe muni d'un repère orthonormé direct (O ;⃗u ; ⃗v ) .
zC − z A
3.a) Calculer le module et l'argument de Z=
z B −z A
3.b) En déduire la nature du triangle ABC.
Term. S – Ch. 9. Les nombres complexes 2
© Abdellatif ABOUHAZIM.
Lycée Fustel de Coulanges - Massy
www.logamaths.fr
Page 7/10
1°) Soit A le point d'affixe z A=3−2i . On a les équivalences suivantes :
∣z−3+2 i∣=5 (ssi) ∣z− z A∣=5
(ssi) AM = 5
(ssi) M ∈C (A ;5) .
Conclusion : E1 est le cercle de centre A et de rayon r = 5.
2°) Soit A le point d'affixe z A=3−2i et B le point d'affixe z B =−1+i On a les
équivalences suivantes :
∣z−3+2i∣=∣z+1−i∣ (ssi) ∣z− z A∣=∣z−z B∣
(ssi) AM = BM
(ssi) M est équidistant de A et de B
(ssi) M appartient à la médiatrice du segment [AB].
Conclusion : E2 est la médiatrice du segment [AB].
3°.a) Soient A, B et C trois points d'affixes z A=3−2i , z B=−1+i et z C =6+2i .
On a :
z − z (6+2i )−(3−2 i) 3+4i
3+4i
3+4 i
1
Z= C A =
=
= 2
=
= =−i
z B −z A (−1+i)−(3−2i ) −4+3i i ×4+3i i (4 i+3) i
Par conséquent : ∣Z∣=1 et arg (Z)= −π [2π] .
2
AC
=1 équivaut à AB = AC.
3°.b) D'une part, ∣Z∣=1 équivaut à
AB
Ce qui signifie que le triangle ABC est isocèle en A.
D'autre part : arg (Z )= −π équivaut à (⃗
AB ; ⃗
AC )= −π [2π] .
2
2
⃗
⃗
Ce qui signifie que les vecteurs AB et AC sont orthogonaux. Donc, le triangle
ABC est rectangle en A.
Conclusion : Le triangle ABC est isocèle-rectangle en A.
II. Forme exponentielle
2.1) Étude d'une fonction particulière
On considère la fonction définie sur ℝ et prend ses valeurs dans ℂ de la manière
suivante f : θ a f (θ) = cos θ + i sin θ.
D'après le 1° du théorème 1, nous avons :
cos (θ +θ' ) + i sin (θ +θ' ) = (cos θ + i sin θ) (cos θ' + i sin θ' ).
Par conséquent, on a :
f (θ+θ ' )= f (θ)× f (θ' )
Pour tous θ , θ ' ∈ℝ :
Ceci signifie que la fonction f vérifie la même relation fonctionnelle que la fonction
exponentielle. Donc, il existe un nombre k tel que, pour tout θ∈ℝ : f (θ)=e k θ ,
avec k = f ' (0) . On calcule f ' (θ) = – sin θ + i cos θ et k = f ' (0)=i . Par suite :
pour tout θ∈ℝ : f (θ ) = eiθ et par suite
Term. S – Ch. 9. Les nombres complexes 2
© Abdellatif ABOUHAZIM.
eiθ = cos θ + i sin θ.
Lycée Fustel de Coulanges - Massy
www.logamaths.fr
Page 8/10
2.2) Forme exponentielle d'un nombre complexe
Définition 1.
Pour tout nombre θ∈ℝ , on note : eiθ = cos θ + i sin θ.
Par conséquent, tout nombre complexe z = r (cos θ + i sin θ ) de module r et
d'argument θ s'écrit sous la forme :
z = r eiθ (Attention r ⩾0 et θ∈ℝ )
Cette écriture s'appelle la forme exponentielle ou la notation exponentielle du
nombre complexe z.
D'après le théorème 1, nous pouvons énoncer sous la forme exponentielle, les mêmes
propriétés écrites sous la forme trigonométriques :
Théorème 3.
∗+
Pour tous nombres r , r 1, r 2 ∈ℝ et θ , θ1, θ2 ∈ℝ , on a :
1°) ∣e i θ∣=1 et arg (e i θ)=θ . Nous avons bien sûr : e i 0=e 0=1
2°)
3°)
iθ1
i θ2
i (θ1+θ2 )
r 1 e ×r 2 e =r 1 r 2 e
r1 e
iθ1
r2 e
iθ2
=
r 1 i(θ −θ )
×e
r2
1
2
Démonstration :
Ce sont des conséquences directes du théorème n°1.
Corollaires
1°) Formule de MOIVRE : Pour tout θ∈ℝ et n∈ℤ :
iθ n
(e ) =e
i nθ
n
ou encore
(cosθ+i sin θ) =cos(n θ)+i sin(n θ)
iθ
2°) Formules d'EULER :
e +e
cos θ=
2
−i θ
iθ
e −e
et sin θ=
2i
−i θ
3°) Formules trigonométriques : Pour tous réels a et b, on a :
Formules d'addition :
Formules de duplication :
a) cos(a+b)=cos a cos b−sin a sin b
c) cos(2 a)=cos2 a−sin 2 a
b) sin (a+b)=sin a cos b+cos a sin b
d) sin (2 a)=2sin a cos a
Démonstration :
1°. a) Nous démontrons d'abord le résultat pour n∈ℕ . On fait un raisonnement par
récurrence. Pour chaque entier n, on appelle Pn la proposition logique
Pn : [ (e i θ)n =e i n θ ].
Term. S – Ch. 9. Les nombres complexes 2
© Abdellatif ABOUHAZIM.
Lycée Fustel de Coulanges - Massy
www.logamaths.fr
Page 9/10
i) Initialisation.
Pour n = 0, (e i θ)0=1=e 0=e i×0×θ Donc P0 est vraie.
(On aurait pu commencer également à n = 1).
ii) Hérédité.
Soit n∈ℕ . Supposons que Pn est vraie. C'est-à-dire : (e i θ)n =e i n θ .
Mais alors : (e i θ)n+1=(e i θ )n×e i θ
par définition des la puissance (n+1)
i θ n+1
i n θ+i θ
d'après l'hypothèse de récurrence
(e ) =e
i θ n+1
i n θ+i θ
d'après la propriété 2°) du théorème 3
(e ) =e
i θ n+1
i( n+1)θ
D'où :
en mettant θ en facteur.
(e ) =e
Donc Pn+1 est vraie.
Par conséquent : Pour tout n∈ℕ : (e i θ)n =e i n θ .
1°. b) Montrons maintenant que le résultat est vrai pour n∈ℤ et n < 0.
On pose n' = – n. Alors n ' ∈ℕ . On peut donc appliquer la propriété avec n' > 0.
1
1
1
1
iθ n
inθ
On a : (e ) = i θ −n = i θ n' = i n' θ = −i n θ =e
.
CQFD
(e )
(e )
e
e
Conclusion . : Pour tout n∈ℤ : (e i θ)n =e i n θ .
2°) Formules d'Euler : On calcule d'abord e−i θ=cos θ−i sin θ=e i θ
On sait que : e i θ=cos θ+i sin θ (1)
et e−i θ=cos θ−i sin θ (2)
– En additionnant membre à membre (1)+(2), nous obtenons :
e iθ+e−i θ
iθ
−iθ
e +e =2 cos θ . D'où le résltat : cos θ=
2
– En soustrayant membre à membre (1)+(2), nous obtenons :
e iθ −e−i θ
iθ
−iθ
CQFD
e −e =2 isin θ . D'où le résltat : sin θ=
2i
3°) On écrit : e ia =cos a+i sin a et e i b=cos b+i sin b
D'après le théorème 3, on a d'une part : e i( a+b)=cos(a+b)+i sin (a+b) (3)
et d'autre part : e i( a+b)=(cos a+i sin a)(cos b+i sin b)
En développant le produit et en regroupant les parties réelle et imaginaire, on obtient:
e i( a+b)=( cos a cos b−sin a sin b )+i ( sin a cos b+cos a sin b ) (4)
Les deux nombres complexes définis dans (3) et (4) sont égaux. Donc, par
identification, leurs parties réelles sont égales et leurs parties imaginaires sont
égales.D'où le résultat :
a) Re( e i( a+b) ) = cos(a+b)=cos a cos b−sin a sin b
b) Im( e i( a+b) ) = sin (a+b)=sin a cos b+cos a sin b .
CQFD
Pour les formules de duplication, il suffit de prendre b=a dans les formules ci-dessus.
OUF !
Term. S – Ch. 9. Les nombres complexes 2
© Abdellatif ABOUHAZIM.
Lycée Fustel de Coulanges - Massy
www.logamaths.fr Page 10/10