Rappels maths IMRT

Rappels Mathématiques
 Puissances
Remarque :
Les puissances de 10 sont un cas particulier des règles précédentes. Il suffit de remplacer a par 10.
De plus, on a par exemple 105 = 1 00 000 et 10-5 = 0, 00001.
Fonctions trigonométriques :
 On utilisera les fonctions sinus ( notée sin ), cosinus ( notée cos ) et tangente ( notée tan ).
 La fonction tangente peut se déduire des deux premières :
sin( )
tan( ) cos( )
x
xx
 Ces fonctions sont périodiques .
la période pour les fonctions sinus et cosinus est
2
; on en déduit donc
sin( 2 ) sin( )xx
; de même,
sin( 4 ) sin( 2 ) sin( )xxx
…en généralisant, on obtient :
sin( 2 ) sin( )x n x
, n étant un nombre entier positif ou négatif.
De la même façon, on a :
cos( 2 ) cos( )x n x
, n étant un nombre entier positif ou négatif.
la période pour la fonction tangente est ; on a donc:
tan( ) tan( )x n x
, n étant un nombre entier
positif ou négatif.
Quelques valeurs remarquables pour les fonctions cosinus et sinus .
Les fonctions sinus et cosinus évoluent entre +1 et -1.
sin( ) sin( . )O n O
sin( ) sin( 2. . ) 1
22
n
sin( ) sin( 2. . ) 1
22
n
cos( ) cos(2. . ) 1On
cos( ) cos( . ) 0
22
n
cos( ) cos( 2. . ) 1n
On peut retrouver facilement ces valeurs grâce au cercle trigonométrique, de rayon 1.
Définition : x étant un nombre non nul, et n un nombre entier non nul, la puissance n-ième de x est le
produit de n facteurs identiques à x :
x n = x
x
……
x. On a n facteurs et n est l’exposant.
Règles : Pour a non nul
1. a0 = 1 et a1 = a
2. a -1 =
a
1
( inverse de a ) et a-n =
n
a
1
3. a n
a p = a n + p et
p
n
a
a
a n – p
4. ( a n ) p = a n p
5. ( a
b ) n = a n
b n et
n
b
a
=
n
n
b
a
cos(x)
sin(x)

 Cas particulier des grandeurs périodiques dans le temps …très fréquentes en physique :
Selon le théorème de FOURIER, une grandeur périodique, de période T, peut
toujours se décomposer en une somme de fonctions sinusoïdales ( ou cosinusoïdales ) :
on étudiera donc plus particulièrement les grandeurs variant de façon sinusoïdale ( ou
cosinusoidale ) dans le temps .
Une telle fonction peut s’écrire :
2
( ) sin( )G t A t
T
A est l’amplitude de G(t)
( G(t) oscille donc entre +A et –A ) ; sa phase à l’origine.
On sait par ailleurs que la fréquence de G(t) ( notée  ) est telle que
1
T
, on
peut par donc exprimer également G(t) ainsi
( ) sin(2 . )G t A t
 Remarque : on peut également définir la pulsation de G(t) ( notée  ) et telle
que
2
2. T
; on a alors
( ) sin( . )G t A t
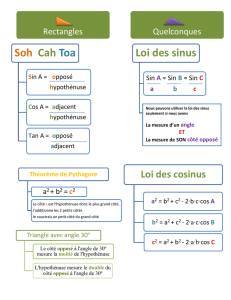
Théorème de Pythagore :
A B
 Trigonométrie dans le triangle rectangle :
Dans le triangle ABC, rectangle en A, on a :
 BC est l’hypothénuse du triangle ABC rectangle en A.
 AB est le côté adjacent de l’angle
B
et le côté opposé de l’angle
C
.
 AC est le côté adjacent de l’angle
C
et le côté opposé de l’angle
B
.
BC
AB
ehypothénus
adjacent
B cos
et
BC
AC
ehypothénus
adjacent
C cos
BC
AC
ehypothénus
opposé
B sin
et
BC
AB
ehypothénus
opposé
C sin
AB
AC
adjacent
opposé
B tan
et
AC
AB
adjacent
opposé
C tan
On pourra retenir SOHCAHTOA (sinus :opposé sur hypothénuse ; cosinus :adjacent sur hypothénuse et
tangente :opposé sur adjacent)
 Equation de droite et proportionnalité
Dans un repère, l’équation de la droite D passant par les points A ( xA ;yA ) et B ( xB ; yB ) est :
baxy
.
 a est appelé le coefficient directeur de la droite D et on a :
AB
AB xx yy
a
.
 b est appelé l’ordonnée à l’origine ( c’est la valeur de y quand x = 0 )
Remarque : Si b = 0 alors l’équation de D devient
axy
. Cette droite passe alors par l’origine du repère et il y
a proportionnalité entre x et y : Ce n’est que dans ce cas qu’on peut utiliser la règle de trois.
C
Dans le triangle ABC rectangle en A, d’après le théorème de Pythagore, on
a : AB² + AC² = BC².
Si dans le triangle ABC, on a AB² + AC² = BC² alors, d’après la réciproque du
théorème de Pythagore, le triangle ABC est rectangle en A.