Chapitre 6 Dérivation et mathématiques « appliquées » (

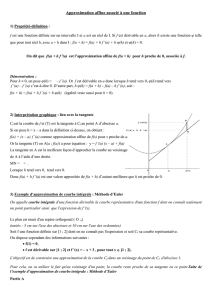
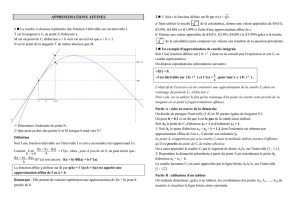
Chapitre 6
Dérivation et mathématiques « appliquées » ( pour la physique aussi)
I) Formule d’ apprixomation affine :
1) théorème :
On considère une fonction définie sur D et a  D
Les deux propriétés suivantes sont équivalentes :
(1) f est dérivable en a
(2) Il existe une fonction  (h) tel que pour tout h tel que a + h  D :
lim(h)0
f( a + h ) = f(a) + h f ’(a) + h  (h) avec : h0
preuve :
(1) implique (2) :
La plus “difficile” : il faut construire la fonction  (h)
« analyse » : si  (h) existe , alors nécessairement :
f(a h) f(a)

h
donc
(h) =
- f ’(a)

« synthèse » : vérifions que (h) vérifie les conditions demandées :
a)
b) vérifions que l’ égalité demandée est vérifiée .
réciproque : (2) implique (1) … C’ est en fait plus facile. On suppose (2) vraie et on
démontre que f est bien dérivable en a .
si (2) est vraie alors : f(a + h) – f (a) =
f(a h) f(a)
h
donc
=
donc f est bien dérivable en a
donc
lim
h 0
f(a h) f(a)
h
=
VOCABULAIRE :
l’ égalité du (2) s’ appelle « formule d’ approximation affine de f en a » .
f( a + h ) = f(a) + h f ’(a) + h  (h)
Le terme en gras est affine en h .
Le terme en italique est négligeable devant un h si h petit
Un(e) physicien(ne) écrira ( sans rigueur !) f( a + h )  f(a) + h f ’(a) si h petit
COMMENTAIRES :
Si f est continue en a ,
Si f est dérivable en a
lim
h0
f ( a + h ) = f (a) f( a + h )  f(a) (approx. d’ ordre 0 )
f( a + h )  f(a) + h f ’(a)
(approx. d’ ordre 1 )
Quelle approximation est la plus précise ??
Exemple 1 :
a) On choisit f(x) = x² et a = 1 .
Alors f ( 1 + h ) 
f(1 + h) 
(apprixomation d' ordre 0 )
(approx.d' ordre 1)
réellement , f ( 1 + h ) =
b) illustration graphique :
Exemple 2 : f(x) = x 3 et a = 2
soit f(2 + h) = ( 2 + h) 3

Réellement , f ( 2 + h ) = ( 2 + h) 3 =
II)Petits accroissements – Ecriture différentielle :
Les écritures de ce paragraphe servent surtout pour la physique .
La formule d' apprixomation affine en a donne :
f( a + h) – f(a)  h f ' (a)
f(a h) f(a)
h
 f ' (a) (2)
(1) ou encore :
Ces deux apprixomations reviennent pour la 1ere à négliger ce qui est petit devant h ,
et pour la deuxième à utiliser directement la notion de limite !!!
Considérons une variable physique f qui dépend du temps , noté t .
Le physicien note :
et
Ainsi h =
l' accroissement de la variable f
l' accroissement du temps ou intervalle de temps .
, on étudie ce qui se passe entre t et t +
Les formule (1) et (2) peuvent donc se noter :

. f ' (t)
(1)
 f ' (t) (2)
Le physicien a donc logiquement noté :
f ' (t) = (limite du quotient de « petits accroissements » !!! )
Exemple 1 ( très important) :
On suppose qu' un objet se déplace le long d' un axe orienté . Apres avoir fixé une origine des
temps et du repère , on appelle x(t) la position de l' objet à l' instant t .
représente x(t + ) - x(t) = distance parcourue pendant l' intervalle
Ainsi : la grandeur
représente : la vitesse ....
et la grandeur x' (t) =
=
représente la vitesse ....
Ce qui signifie physiquement que la limite de la
.....
est la ......
Si on va plus loin , la vitesse v(t) peut se dériver !
On appelle accélération a(t) =
=
notée :
ou a(t) = v ' (t) = x '' (t)
Voir DM page 73 exercice 4 du livre de Mathématiques .
Exemple 1 bis : vitesse de réaction en chimie :
En TP de chimie , vous lisez directement la vitesse de réaction
en lisant
le coefficient directeur de la tangente .
Exemple 2 : (déjà vu) :
Dans la loi de désintégration , le nombre de noyaux se désintégrant entre t et t +
proportionnel à l' intervalle de temps
ET au nombre de noyaux à l' instant t .
est
Appelons N(t) le nombre de noyaux présents à l' instant t .
Ainsi
soit :
=
=
ce qui donne par passage à la limite quand
tend vers 0 :
On obtient une équation différentielle vérifiée par fonction N(t) .
Une equa. différentielle est une équation vérifiée par une fonction et ses dérivées successives.
Equation différentielle du 1er ordre :
exemple en physique :
Equation différentielle du 2eme ordre :
exemple en physique :
III) Principe de la méthode d' Euler :
Il sera étudié sur l' exemple fondamental du programme , traité en TP infopar tableur .
D' autres problèmes pourront être étudiés en DM ou exercices .
On cherche les fonctions f vérifiant le problème suivant :
pour tout x réel , f ' (x) = f(x) et f(0) = 1 noté (E)
La méthode d' Euler est une méthode numérique permettant de « calculer » une solution
approchée de « la solution de (E) ».
Principe :
1) On écrit l' approximation affine en a = 0
f( a + h ) = f (a) + h f ' (a) + h
devient :
comme f vérifie (E) , alors f(h) =
+ h
soit
f(h) ≈
2) On écrit l' approximation en a = 0 + h en se servant de l' approximation précédente :
f( a + h ) = f (a) + h f ' (a) + h
comme f vérifie (E) , f (
devient :
) =
+ h
3) On écrit l' approximation en a = 0 + 2h :
f( a + h ) = f (a) + h f ' (a) + h
comme f vérifie (E) , f (
soit f(
)≈
soit f(
)≈
devient :
) =
+ h
etc... On peut prouver par récurrence que f ( nh) ≈
Numériquement avec un pas h = 0,1 on obtient :
x
0
0,1
0,2
0,3
Solution
1
approchée de (E)
Exercice : appliquer la méthode d' Euler sur le problème suivant .
f(0) = 0 et f ' (x) = x²
(pas h = 0,1) ( on calculera 4 valeurs ! )
avec n entier > 0