Approximations affines

APPROXIMATIONS AFFINES
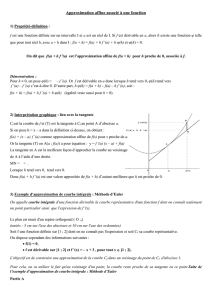
1  La courbe ci-dessous représente une fonction f dérivable sur un intervalle I.
T est la tangente à C
f
au point A d'abscisse a.
M est un point de C
f
d'abscisse a + h où h est un réel tel que a + h ∈ I.
N est le point de la tangente T de même abscisse que M.
1/ Déterminer l'ordonnée du point N.
2/ Que peut-on dire des points N et M lorsque h tend vers 0 ?
Définition
Soit f une fonction dérivable sur l'intervalle I et soit a un nombre réel appartenant à I.
Comme h → 0 lim f(a + h) – f(a)
h = f '(a) , alors , pour h proche de 0, on peut écrire que :
f(a + h) – f(a)
h ≈ f '(a) soit encore : f(a + h) ≈
≈≈
≈ f(a) + h f '(a).
La fonction affine g définie sur r par g(h) = f '(a) h + f(a) est appelée une
approximation affine de f en a + h.
Remarque : Elle permet de calculer rapidement une approximation de f(a + h) pour h
proche de 0.
2  1/ Soit r la fonction définie sur r par r(x) = x.
a/ Sans utiliser la touche de la calculatrice, donner une valeur approchée de f(4,01),
f(3,99), f(4,001) et f(3,999) à l'aide d'une approximation affine de r.
b/ Donner une valeur approchée de f(4,01), f(3,99), f(4,001) et f(3,999) grâce à la touche
de la calculatrice puis comparer ces valeurs aux résultats de la question précédente.
3  Un exemple d'approximation de courbe intégrale
Soit f une fonction définie sur ] 0; +∞ [ dont on ne connaît pas l'expression et soit C
f
sa
courbe représentative.
On dispose cependant des informations suivantes :
• f(1) = 0,
• f est dérivable sur ] 0; +∞
∞∞
∞ [ et f '(x) = 1
x , pour tout x ∈
∈∈
∈ ] 0; +∞
∞∞
∞ [.
L'objectif de l'exercice est de construire une approximation de la courbe C
f
dans un
voisinage du point de C
f
d'abscisse 1.
Pour cela, on va utiliser le fait qu'au voisinage d'un point, la courbe reste proche de sa
tangente en ce point (cf approximations affines).
Partie A : mise en œuvre de la démarche
On décide de partager l'intervalle [1;4] en 30 parties égales de longueur 0,1.
On pose h = 0,1 et on dit que h est le pas de la subdivision réalisée.
Soit A
0
le point de C
f
d'abscisse x
0
= 1 et d'ordonnée y
0
= 1.
1/ Soit A
1
le point d'abscisse x
1
= x
0
+ h = 1,1 dont l'ordonnée est obtenue par
approximation affine de f en x
1
. Calculer son ordonnée y
1
.
Le point A
1
n'appartient pas à la courbe C
f
mais la méthode utilisée permet d'affirmer
qu'il est proche du point de C
f
de même abscisse.
On a ainsi approché la courbe C
f
par le segment de droite A
0
A
1
sur l'intervalle [1 ; 1,1].
2/ Reproduire la démarche précédente à partir du point A
1
en introduisant le point A
2
d'abscisse x
2
= x
1
+ h.
La courbe inconnue C
f
est ainsi approchée par la ligne brisée A
0
A
1
A
2
sur l'intervalle
[1 ; 1,2]
Partie B : utilisation d'un tableur
On souhaite déterminer, grâce à un tableur, les coordonnées des points A
0
, A
1
, …, A
30
de
manière à visualiser la ligne brisée ainsi construite.

APPROXIMATIONS AFFINES
Ouvrir le fichier méthode d'Euler2 : la fenêtre suivante apparaît :
1/ Définir les cellules D5 et E5 en fonction des cellules D4, E4 et A2 de manière à ce
qu'une simple recopie vers le bas de la ligne 5 permette d'obtenir les coordonnées des 31
points recherchés.
2/ Sélectionner les cellules des colonnes D et E complétées puis l'outil "diagramme".
Choisir ensuite comme type de diagramme : XY (dispersion) : points et lignes.
Imprimer la représentation graphique obtenue.
Ce procédé de construction d'une approximation de courbe utilisant les approximations
affines s'appelle la méthode d'Euler.
Partie C
Soit f la fonction définie sur ] 0; +∞ [ par f(x) = ln x, où ln est une fonction encore
inconnue en classe de 1
ère
mais dont on constate la présence sur les calculatrices
scientifiques : touche ln
1/ Construire dans la colonne F les valeurs de ln (x
k
) pour toutes les valeurs de k
considérées (dans un tableur cette fonction se note LN( )).
2/ Utiliser à nouveau l'outil "diagramme" pour faire apparaître dans le même repère que
précédemment, l'allure de la courbe représentative de la fonction f dans l'intervalle [1 ; 4]
On admettra que la fonction f ainsi définie est la fonction dont on a cherché à approcher
la courbe représentative.
L'approximation obtenue dans la partie C est-elle de bonne qualité ?
Comment aurait-on pu améliorer le résultat ?
Remarques : On appelle courbe intégrale d'une fonction dérivable la courbe
représentative d'une fonction f dont on connaît seulement un point particulier ainsi que
l'expression de f '(x).
La fonction f définie ci-dessus s'appelle la fonction logarithme népérien.
(programme de terminale)