TRIGONOMÉTRIE ET ANGLES ORIENTÉS

1ère STrigonométrie Cours
TRIGONOMÉTRIE ET ANGLES ORIENTÉS
Première S - Chapitre 5
Table des matières
I Le cercle trigonométrique et le radian 2
I1 Lecercletrigonométrique ..................................... 2
I2 Leradian .............................................. 3
II Cosinus et sinus d’un réel 3
II 1 Cosinus, sinus et cercle trigonométrique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
II2 Propriétés.............................................. 4
II 3 Valeurs particulières à connaître . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
II 4 Formules de correspondances . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
III Angles orientés 5
III1Définition .............................................. 5
III2Propriétés.............................................. 5
III 2 a Vecteurs colinéaires et angles orientés . . . . . . . . . . . . . . . . . . . . . . . . . . 5
III2bRelationdeChasles .................................... 5
III 2 c Conséquences de la relation de Chasles . . . . . . . . . . . . . . . . . . . . . . . . . . 5
III 3 Mesure principale d’un angle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
IV Résolution d’équations trigonométriques 7
N. Peyrat Lycée Saint-Charles 1/ 7

1ère STrigonométrie Cours
Dans tout le chapitre, le plan est muni d’un repère orthonormé (O;~ i,~ j).
I Le cercle trigonométrique et le radian
I 1 Le cercle trigonométrique
Définition
On appelle cercle trigonométrique le cercle Cde centre O et de rayon 1 sur lequel on choisit un
sens de parcours, appelé le sens direct.
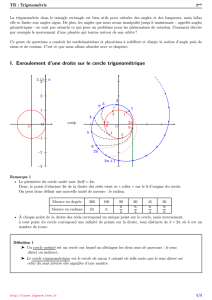
Enroulement de la droite des réels :
Soit dla tangente à Cau point I(1 ; 0).
Alors tout point Nde dest repéré par un unique réel x.
(dpeut être assimilé à un axe gradué)
En enroulant la droite dsur le cercle C, on associe à tout réel xun unique
point M(x)du cercle Cet on dit que xest une mesure de l’angle ÷ IOM.
Remarque :
La longueur d’un cercle de rayon Rest donnée par la formule 2πR.
Or le cercle trigonométrique a pour rayon R= 1, donc sa longueur est de 2π.
Son demi-cercle a donc pour longueur πet son quart de cercle a pour longueur π
2.
Exemple :
Tracer un cercle trigonométrique et placer les points I(0),J(π
2),K(π),L(3π 2),M(2π),N(−π 2),
P(−3π
4).
Propriété
Pour tout réel xet pour tout entier relatif k, les points M(x)et M0(x+k×2π)du cercle trigono-
métrique sont confondus.
Exemple :
Dans l’exemple précédent, Iet Msont confondus, et Net Lsont confondus.
N. Peyrat Lycée Saint-Charles 2/ 7

1ère STrigonométrie Cours
I 2 Le radian
Définition
Le radian est l’unité de mesure des angles tel que la mesure en radian d’un angle est égale à la
longueur de l’arc que cet angle intercepte sur un cercle de rayon 1.
Exemple :
Faire un cercle trigo et placer un point M(x)tel que ÷ IOM =α.
L’angle ÷ IOM de mesure αdegrés intercepte l’arc ¯ IM de longueur x.
On dit alors que l’angle ÷ IOM mesure xradians.
Remarques :
Un angle plat mesure πradians.
Un angle droit mesure π
2radians.
Un angle nul mesure 0radians.
Propriété (admise)
Les mesures en degré et en radian d’un angle sont proportionnelles.
Exemple :
degré 0 180 90 60 45 30
radian 0ππ
2
π
3
π
4
π
6
II Cosinus et sinus d’un réel
II 1 Cosinus, sinus et cercle trigonométrique
Propriété
Soit Cle cercle trigonométrique de centre O dans un repère orthonormé
direct (O;~ i,~ j).
Soit xun réel et Mle point de Ctel que (
~
i, −−→ OM) = xradians.
Le point Ma alors pour coordonnées :
M(cos x; sin x)
Autrement dit : −−→ OM = cos x×~ i+ sin x×~ j.
Démonstration :
Trigonométrie dans un triangle rectangle.
N. Peyrat Lycée Saint-Charles 3/ 7

1ère STrigonométrie Cours
II 2 Propriétés
Propriété
Pour tout réel x, on a :
−16cos x61;−16sin x61;cos2x+ sin2x= 1
Démonstration :
Faire une démonstration rapide et à l’aide du triangle rectangle.
Propriété (admise)
• ∀x∈R,sin(−x) = −sin x.
• ∀x∈R,cos(−x) = cos x.
• ∀x∈R,cos(x+k×2π) = cos(x)et sin(x+k×2π) = sin(x).
II 3 Valeurs particulières à connaître
II 4 Formules de correspondances
Propriété (admise)
Pour tout réel x:
sin Åπ
2−xã= cos x;cos Åπ 2−xã= sin x
sin Åπ
2+xã= cos x;cos Åπ 2+xã=−sin x
sin(π−x) = sin x;cos(π−x) = −cos x
sin(π+x) = −cos x;cos(π+x) = −sin x
N. Peyrat Lycée Saint-Charles 4/ 7

1ère STrigonométrie Cours
III Angles orientés
III 1 Définition
Définition
Soit Cun cercle trigonométrique de centre Odans un repère orthonormé direct (O;~ i,~ j).
Pour tous points Met Nde C, on appelle mesure de l’angle orienté (−−→ OM, −−→ ON)la famille de nombres
sous la forme x+k×2π(k∈Z), où xest la longueur de l’arc ˘ MN.
Faire une figure.
III 2 Propriétés
III 2 a Vecteurs colinéaires et angles orientés
•~u et ~vsont colinéaires et de même sens ⇔(~u,~v) = 0 + k×2π,k∈Z.
•~u et ~vsont colinéaires et de sens contraire ⇔(~u,~v) = π+k×2π,k∈Z.
•~u et ~vsont colinéaires ⇔(~u,~v) = 0 + k×π,k∈Z.
III 2 b Relation de Chasles
Propriété
Pour tous vecteurs ~u,~vet ~w non nuls du plan, on a :
(~u, ~w)=(~u, ~v) + (~v, ~w)
III 2 c Conséquences de la relation de Chasles
Propriété
Pour tous vecteurs ~u et ~vnon nuls :
1) (~u,~v) = −(~v, ~u).
2) (~u, −~v) = (~u, ~v) + π.
3) (−~u,~v) = (~u,~v) + π.
4) (−~u, −~v) = (~u, ~v).
Faire une figure en-dessous de chaque propriété.
N. Peyrat Lycée Saint-Charles 5/ 7