10 Angles 6èA

CH X ANGLES
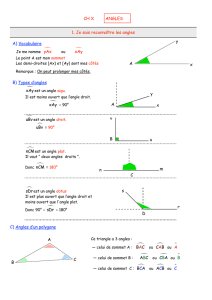
1. Je sais reconnaître les angles
A) Vocabulaire
Je me nomme
yAx
ou
xAy
Le point A est mon sommet
Les demi-droites [Ax) et [Ay) sont mes côtés
Remarque : On peut prolonger mes côtés.
B) Types d’angles
xAy
est un angle aigu.
Il est moins ouvert que l’angle droit.
xAy
≺ 90°
uBv
est un angle droit.
uBv
= 90°
nCM
est un angle plat.
Il vaut “ deux angles droits ”.
Donc
nCM
= 180°
sDr
est un angle obtus.
Il est plus ouvert que l’angle droit et
moins ouvert que l'angle plat.
Donc 90° ≺
sDr
≺ 180°
C) Angles d’un polygone
Ce triangle a 3 angles :
— celui de sommet A :
BAC
ou
CAB
ou
A
— celui de sommet B :
ABC
ou
CBA
ou
B
— celui de sommet C :
BCA
ou
ACB
ou
C
x
A
y
A
C
B
Ax
y
C
m
n
D
r
s
Bu
v

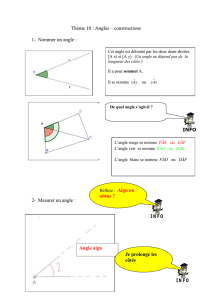
2. Je sais utiliser le rapporteur.
A) L’unité d’angle
L’unité d’angle est le degré. Le symbole du degré est °
Voici un angle de 1° et un angle de 5°.
B) L’angle droit
BAC
= 90°
C) Mesurer un angle : On utilise un rapporteur
AOB
= 120°
Exemples :
D) Tracer un angle de mesure donnée
Construire un angle de 25° et un angle de 138°
1°) On fait coïncider le centre du rapporteur
avec le sommet O de l’angle
2°) On positionne le 0°
sur le côté [OA) de l’angle
3°) On lit la mesure de l’angle sur le côté [OB)
AC
B
27°
130°
28°
110°
42°

A
x'
A'
1°) Je trace un premier côté de l’angle : [A'x').
Ax
y
2°) Je trace deux arcs de même rayon l’un de centre A et l’autre de centre A'.
y
x
A
T
R
x'
A'
M
3°) Je prends l’écartement entre R et T et je le reporte à partir du point M.
Il coupe le premier arc en N. Je trace le deuxième côté de l’angle : [A'N)
R
T
A
y
xx'
A'
N
M
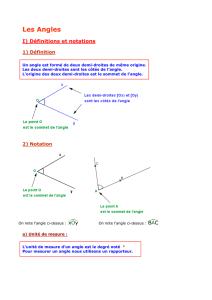
3. Angles égaux. Reproduire un angle au compas.
Reproduire un angle
On peut mesurer l'angle.
On peut utiliser le compas.

4. La bissectrice d’un angle. Je sais calculer un angle.
A) Définition
La bissectrice d’un angle est la demi-droite qui partage cet angle en deux angles égaux.
B) Tracer la bissectrice
Avec le rapporteur
C) Calculer un angle
1°) Calculer l' angle
DAE
2°) Construire les bissectrices
[Ay) de l’angle
DAE
et [Ax) de l’angle
3°) Démontrer que [Ax) ⊥ [Ay)
Solution
1°)
DAE
= 180° - 62°
DAE
= 118°
2°) On trace les bissectrices
3°) On calcule l'angle
xAy
xAy
= ( 62° : 2 ) + ( 118° : 2 )
xAy
= 31° + 59°
xAy
= 90°
Conclusion : [Ax) ⊥ [Ay)
34° : 2 = 17°
AC
B
17°
17°
A
E
B
D
62°
BAD
A
E
B
D
x
y
118°
62°