LES ANGLES

LES ANGLES
CONTENU COMPETENCES EXIGIBLES
Angles
Utiliser le vocabuaire sur les angles.
Sur papier blanc et sans que la méthode soit imposée : reproduire un angle.
Comparer des angles.
Utiliser un rapporteur pour déterminer la mesure en degré d’un angle et construire
un angle de mesure donnée en degré.
Connaître et utiliser la définition de la bissectrice.
Tracer la bissectrice d’un angle au rapporteur.
PREREQUIS : QCM PAGE 155
A CTIVITE 1
I) NOTIONS D ’ ANGLES :
1) D EFINITION :
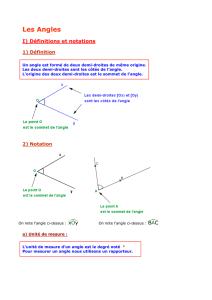
Un angle est formé par 2 demi-droites (qui sont les côtés de l’angle), et d’un
sommet qui est l’origine de ces deux demi-droites.
2) Exemples :
3)
On note l’angle :
xOy
ou
yOx
On note l’angle :
BAC
ou
CAB
1- L’angle
IAJ
2- …………….
3- …………….
4- …………….
5- …………….
6- …………….
7- …………….
8- …………….
1
Exercice 1,2 page 164

LES ANGLES
A CTIVITE 2
Sur chacune des huit pendules ci-dessous, les aiguilles forment un angle numéroté de 1 à 8.
1) Comment appelle-t-on l’angle 6 ?
……………………………………………………….
2) Quels sont les angles saillants ayant une mesure plus petite que l’angle 6 ?
……………………………………………………….
3) Quels sont les angles rentrants ayant une mesure plus grande que l’angle plat ?
………………………………………………………..
4) Comment appelle-t-on l’angle 4 ?
……………………………………………………….
5) Quels sont tous les angles aigus qui apparaissent sur les pendules ?
…………………………………………………….....
6) Quels sont tous les angles obtus qui apparaissent sur les pendules ?
……………………………………………………….
7) Ranger dans l’ordre croissant les angles numérotés de 1 à 8.
………………………………………………..
II) LES ANGLES PARTICULIERS
xOy
= ……….
xOy
= ……….
xOy
= ……….
xOy
= ……….
xOy
= ……….
Angle Nul
(0°) Angle Aigu
(0° à 90°)
Angle Droit
(90°) Angle Obtus (90° à 180°) Angle Plat (180°)
Exercice 5, 6 page 164
O
x
y
O
x
y
x
O
x
y
x
O
x
y
x
O
y

LES ANGLES
III) UTILISATION DU RAPPORTEUR
1) L E RAPPORTEUR :
Le rapporteur n’est pas un instrument de tracé, mais un instrument de mesure.Il est
gradué en degrés (de 0° à 180°).
2) M
ESURER UN ANGLE :
3) C
ONSTRUIRE UN ANGLE :
Graduation
«
extérieure
»
De
0 à 180°
de gauche à
d
roite
Graduation «
intérieure
»
De 0 à 180° de droite à gauche.
Centre
On veut mesurer l’angle
xOy
^ .
On positionne correctement le
rapporteur. On va le faire glisser...
O
x
y
... jusqu’à ce que son centre coïncide
avec le sommet de l’angle.
On va ensuite le faire pivoter...
O
x
y
...jusqu’à ce que le « 0
» d’une des
deux graduations (ici, la graduation
extérieure) se place sur le côté de
l’angle.
On lit alors la mesure de l’angle : 50°
O
x
y
On veut construire un angle xOy
^ qui
mesure 30° à l’aide du rapporteur.
On positionne correctement le
rapporteur
O
x
On repère à l’aide d’un petit point
la position de la graduation désirée.
Ici, il s’agit de la graduation 30°.
On retire le rapporteur, puis on trace à
la règle la demi-droite d’origine O
passant par le repère précédent.
On a construit l’angle xOy
^ qui
mesure 30°
O
x
O
x
y

LES ANGLES
4) E
XEMPLES :
a) À l’aide d’un rapporteur, mesurer dans chacun des cas l’angle
xOy
:
b) Dans chaque cas, tracer la demi droite [
[[
[Ox) ou [
[[
[Oy) pour que l’angle
xOy
ait la mesure
indiquée :
x
y
O
1.
x
y
O
2.
y
O
3.
x
xOy
= 40°
O
x
O
x
xOy
= 70°
O
x
xOy
= 130°
O
y
xOy
= 170°

LES ANGLES
IV) REPRODUCTION D’UN ANGLE AVEC LE COMPAS
PREMIEREMENT DEUXIEMENT TROISIEMMENT QUATRIEMMENT CINQUIEMMENT
On veut reproduire
Cet angle On trace un arc de cercle de centre o.
On obtient les points
B et C qui coupe les
deux demi-droites.
On trace une demi
droite [Au), et l’on
trace un arc de
cercle avec la même
ouverture de compas
Que précédemment
Avec le compas, on
prend l’écartement
entre B et C et l’on
trace l’arc de cercle
de centre B’ et de
rayon BC coupant
l’arc précédent en C’.
Enfin, on trace la
Demi-droite [Av) qui
passe par C’.
V) BISSECTRICE D’UN ANGLE
1- A NGLES A DJACENTS :
Deux angles adjacents ont le même
sommet, un côté commun et sont
situés de part et d’autre de ce côté.
Dans l’exemple ci-contre,
les angles
xOy
et
yOz
sont adjacents
2- D EFINITION DE LA B ISSECTRICE :
La bissectrice d’un angle est la demi-droite qui partage cet angle en deux angles
adjacents de même mesure.
La demi-
droite [Oy) est la bissectrice de
l’angle
xOz
xOy
=
yOz
=
xOz
2
o
x
y
o
x
y
B
C
A
u
B’ B’
A
u
C’
A
B’ u
C’ v
O
z
y
x
O
x
y
z
Dans le dessin ci-dessus, les lignes discontinues
qui se prolongent vers l’horizon partagent la route
en deux angles égaux : Ce sont donc deux bissectrices
Exemple
:
Exemple :