DS de physique de décembre TS2

TS2 Correction DS de Physique décembre 2010
Exercice 1 :
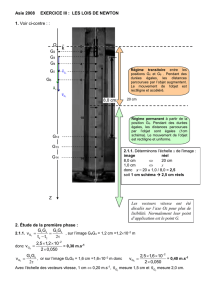
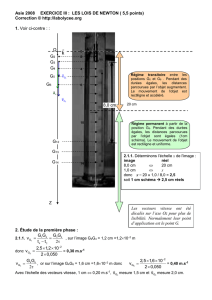
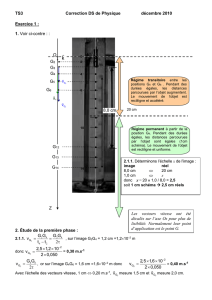
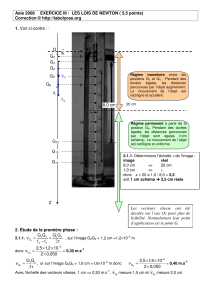
1. Voir ci-contre : :
2. Étude de la première phase :
2.1.
3
2 4 2 4
42 2
GG G G G
vtt
, sur l’image G2G4 = 1,2 cm =1,210–2 m
donc
3
2
G2,5 1,2 10
v2 0,050
= 0,30 m.s-1
5
46
2
GGG
v
, or sur l’image G4G6 = 1,6 cm =1,610–2 m donc
5
2
G2,5 1,6 10
v2 0,050
= 0,40 m.s-1
Avec l’échelle des vecteurs vitesse, 1 cm  0,20 m.s-1,
3
G
v
mesure 1,5 cm et
5
G
v
mesure 2,0 cm.
0
2
4
6
10
14
Z
O
20 cm
Régime transitoire entre les
positions G0 et G8 . Pendant des
durées égales, les distances
parcourues par l’objet augmentent.
Le mouvement de l’objet est
rectiligne et accéléré.
Régime permanent à partir de la
position G9. Pendant des durées
égales, les distances parcourues
par l’objet sont égales (1cm
schéma). Le mouvement de l’objet
est rectiligne et uniforme.
G2
G4
G6
G3
G5
3
G
v
5
G
v
k
4
a
G13
G12
G14
Les vecteurs vitesse ont été
décalés sur l’axe Oz pour plus de
lisibilité. Normalement leur point
d’application est le point G.
2.1.1. Déterminons l’échelle x de l’image :
image réel
8,0 cm  20 cm
1,0 cm  x
donc x = 20  1,0 / 8,0 = 2,5
soit 1 cm schéma  2,5 cm réels
8,0 cm

2.2.
53
53
422
GG
GGv v .k
vv
v
at . .
=
4
a .k
où
k
vecteur unitaire porté par l’axe Oz.
Ainsi :
40,40 0,30
a2 0,050
= 1,0 m.s-2.
Avec l’échelle des accélérations, 1 cm  0,50 m.s-2,
4
a
mesure 2,0 cm.
3. Étude de la deuxième phase
3.1. Durant la seconde phase, en régime permanent, le mouvement est rectiligne et uniforme.
3.2. Première loi de Newton : Dans un référentiel galiléen, un solide soumis à un ensemble de forces qui
se compensent est soit immobile, soit en mouvement rectiligne et uniforme. Et réciproquement.
3.3.
13
12 14
2
GGG
v
. Or sur l’image G12G14 = 2,0 cm = 2,0.10-2 m donc
5
2
G2,5 2,0.10
v2 0,050
= 0,50 m.s-1
Exercice 2 : La grêle
A – CHUTE LIBRE
A.1. Considérons comme système le grêlon dans un référentiel terrestre (supposé galiléen) en chute libre.
Il n’est soumis qu’à son poids.
Appliquons la deuxième loi de Newton :
amP 
ou
amgm o
soit
ago
Par projection sur l’axe Oz vertical, il vient az = go
Or
dt
d
z
az
v
par intégration on obtient vz = go×t + v0z.
Le grêlon tombe sans vitesse initiale, soit v0z = 0 m.s–1 donc : vz = go×t
D’autre part
dt
dz
zv
par intégration on a : z = ½ go×t² + z0.
Or à t = 0 s, le grêlon est en O , donc z0 = 0 m d’où : z = ½ go×t²
A.2. Quand le grêlon atteint le sol, alors z = h = 1500 m, exprimons la date t d'arrivée au sol :
h = ½ go×t² soit
o
gh
t2
remplaçons t par son expression pour trouver la vitesse de chute : vh = go.t =
o
ogh
g2
150080,922v  oh gh
= 171 m.s-1 = 617 km.h-1
Dans le texte, on nous dit que la vitesse d’un grêlon au sol peut atteindre 160 km/h, la valeur obtenue
avec ce modèle de chute libre, n’est pas vraisemblable.
B – CHUTE REELLE
1. FA = ×V×g0 =  
3
3
4r
g0
FA =
80,93,110.
20,3 3
43
2
= 1,8.10-4 N
P = m×go = 13.10-3×9,80 = 0,13 N
Le poids du grêlon est environ 700 fois plus élevé que la poussée d’Archimède, on peut donc négliger
celle-ci devant le poids.

2.a. Appliquons la deuxième loi de Newton au grêlon, dans un référentiel terrestre (supposé galiléen). Le
grêlon est soumis à son poids et à la force de frottement fluide :
amFP 
le poids est vertical dirigé vers le bas
la force de frottement est verticale dirigée vers le haut,
En projetant sur l’axe Oz vertical et dirigé vers le bas il vient : P – F = m×az
Soit :
2
v
v Kgm
dt
d
mo
ou
2
v
v m K
g
dt
do
L’équation différentielle obtenue est bien de la forme
2
v.
vBA
dt
d
avec A = go et B = K / m
2.b. ai = A – B×vi2 a4 = A – B×v42 = 9,80 – 1,56.10-2×17,2² = 5,18 m.s-2
vi+1 = vi + ai×t v5 = v4 + a4×t = 17,2 + 5,18×0,5 = 19,8 m.s-1
2.c. Quand la vitesse limite est atteinte alors celle-ci est constante et
0
v
dt
d
0v2
lim  BA
 2
lim 1056,1 80,9
vB
A
25 m.s-1
B.3.d. On trace l’asymptote à la courbe :
vlim =