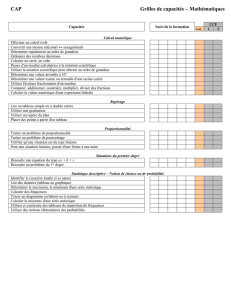
d - Apmep

POLYGONES ET AXES DE
SYMETRIE
RAPPELS :
1) Pour tracer le symétrique A’ d’un point A par rapport à la droite "d".
A
A
A
A’
1 2 3
2) Une figure géométrique possède un axe de symétrie lorsqu’elle se retrouve à la même place
après avoir fait un retournement autour d’une droite.
12
3) En utilisant une symétrie par rapport à une droite (symétrie orthogonale), une figure
géométrique fait un retournement autour d’une droite.
A=A’
B
B’
C
C’
d
TRIANGLES ET AXES DE SYMETRIE :
J’ai dessiné 9 triangles.
Quels sont ceux qui possèdent un axe de symétrie ? (Ils reprennent leur place après un retournement
autour de l’axe de symétrie).
1 2 3 4
87
5
6 9
La figure  possède un axe de symétrie.
La figure  ne possède pas d’axe de
symétrie.
La figure géométrique n’est pas déformée :
Je peux dire que la symétrie par rapport à une
droite (orthogonale) conserve (ne change pas) les
longueurs et les angles.

TRIANGLES ET SYMETRIE ORTHOGONALE
Un triangle isocèle est un triangle qui a un axe de symétrie.
A
B
C
D
d
Exercice
1) Trace en vraie grandeur les triangles isocèles ci-dessous.
1 2 3 4
A
BC
5 cm
7 cm
A
B
C
7 cm
5 cm
A
B
C
4 cm
3 cm
A
B
C
7 cm
3 cm
2) En utilisant les dessins ci-dessus ou en faisant des mesures sur les dessins en vraie grandeur,
calcule le périmètre de chacun des quatre triangles.
AIRE DES TRIANGLES RECTANGLES ET ISOCELES
RAPPEL :
l
L
l
L
l
L
Je découpe le rectangle en deux triangles rectangles. J’assemble les morceaux pour obtenir un
triangle isocèle (ayant un axe de symétrie).
La symétrie orthogonale conserve les aires.
Les deux triangles rectangles ont donc même aire.
La droite "d" est l’axe de symétrie du triangle ABC donc :
1) AB = AC et BD = DC car la symétrie orthogonale
conserve les longueurs.
2) ABC = ACB ; BDA = CDA (angles droits) et
BAD =CAD car la symétrie orthogonale conserve
les angles
3) L’aire du triangle BDA est égale à l’aire du triangle
CDA car la symétrie orthogonale conserve les aires.
Aire d’un rectangle : Longueur
×
largeur
A = L
×
l

3 cm
6 cm
12 cm
3 cm
Exercices :
1) Calcule l’aire des 4 triangles isocèles dessinés précédemment : des tracés ou des mesures
supplémentaires seront parfois nécessaires.
2)
A
BC
D
Utilise ce qui vient d’être fait à la question 2 pour calculer les aires des triangles ci-dessous.
A
B C
1
A
B
C
2
A
B
C
3
A
BC
4
L’aire d’un triangle rectangle est donc égale à la moitié de
l’aire d’un rectangle
Ici : A = (3 cm
×
6 cm) : 2 = 9 cm2
"3 cm
×
6 cm" est le produit des longueurs des côtés de
l’angle droit du triangle.
L’aire d’un triangle isocèle est donc aussi égale à la
moitié de l’aire d’un rectangle
Ici : A = (12 cm
×
3 cm) : 2 = 18 cm2
"12 cm
×
3 cm" est le produit des longueurs de la base
et de la hauteur du triangle.
A l’aide de la perpendiculaire à la droite (BC) passant
par le point A, j’ai découpé le triangle ABC en deux
triangles ABD et ADC.
Après avoir mesuré ce qui est nécessaire, tu vas
calculer l’aire des triangles rectangles ABD et ADC,
puis l’aire du triangle ABC.

AIRE D’UN TRIANGLE
1
A
BC
2
AB
C
3
B
AC
4
A
B
C
5
A
BC
6
A
B
C
7
B
A
C
8
A
B
C
En mesurant ce qui te paraît nécessaire et en traçant ce qui te semble utile, calcule l’aire des 8
triangles de cette feuille.
RAPPELS :
B
DAC
1. L’aire d’un triangle rectangle est la
moitié de l’aire d’un rectangle.
2. L’aire d’un triangle isocèle est la moitié
de l’aire d’un rectangle.

AIRE DE QUADRILATERES
En traçant ce qui te semble utile et en mesurant ce qui te paraît nécessaire, calcule l’aire des 7
quadrilatères ci-dessous.
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
1
2
3
4
7
5
6
RAPPELS :
B
DAC
1. L’aire d’un triangle rectangle est la
moitié de l’aire d’un rectangle.
2. L’aire d’un triangle isocèle est la moitié
de l’aire d’un rectangle.