polygones reguliers

www.mathafr.fr © 05/2014, Mathaf’R, tous droits réservés
Figures construites à l’aide du logiciel de géométrie Geogebra
POLYGONES REGULIERS
3
e
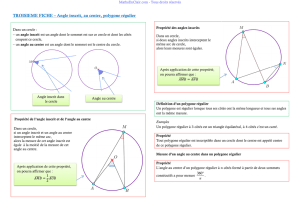
I. Définition
Définition :
Un polygone dont les longueurs des côtés sont égales entre elles
ET dont les mesures des angles intérieurs sont égales entre elles
est appelé un polygone régulier.
Exemple :
Dans la figure ci-contre, ABC est un triangle équilatéral.
Les longueurs AB, BC, CA de ses trois côtés sont égales entre
elles.
Les mesures de ses trois angles (intérieurs)
,
et
sont égales à 60°.
ABC est donc un polygone régulier (à 3 côtés)
Dans la figure ci-contre, EFGH est un carré.
Les longueurs EF, FG, GH et HE de côtés sont égales entre
elles.
Les mesures de ses quatre angles (intérieurs)
,
,
et
sont égales à 90°.
EFGH est donc un polygone régulier (à 4 côtés)
II. Cercle circonscrit à un polygone régulier
Propriété :
Si un polygone est régulier alors on peut tracer un cercle qui passe par chacun de ses sommets.
Définitions :
Le cercle passant par tous les sommets d’un polygone régulier est appelé le cercle circonscrit à
ce polygone régulier.
Le centre du cercle circonscrit à un polygone régulier appelé le centre de ce polygone.
Exemple :
Dans la figure ci-contre, le cercle C passe par tous les
sommets I, J, K, L M, N de l’hexagone régulier IJKLMN.
C est donc le cercle circonscrit à l’hexagone régulier
IJKLMN.
De plus, O est le centre du cercle C . O est donc le centre de
l’hexagone régulier IJKLMN.
C

www.mathafr.fr © 05/2014, Mathaf’R, tous droits réservés
Figures construites à l’aide du logiciel de géométrie Geogebra
III. Mesures d’angles et polygone régulier
Dans cette partie, n désigne un nombre entier.
Propriété :
Dans un polygone régulier à n côtés,
si les côtés d’un angle qui a pour sommet le centre de ce polygone passent par deux sommets
consécutifs de ce polygone, alors la mesure de cet angle est égale à
°
Exemple :
IJKLMN est un hexagone régulier de centre O c’est-à-dire un
polygone régulier à 6 côtés.
De plus, l’angle
a pour sommet le centre O de cet hexagone.
Ses côtés [OL) et [OM) passent par deux sommets consécutifs L
et M de cet hexagone.
Un hexagone ayant 6 côtés, on a :
°
c’est-à-
dire
60°
Méthode :
Pour trouver la mesure des angles intérieurs d’un polygone régulier, on peut utiliser la
propriété donnant la relation entre la mesure d’un angle inscrit et la mesure d’un angle au
centre interceptant un même arc dans un cercle.
Pour cela, on l’applique dans le cercle circonscrit au polygone régulier en observant l’angle au
centre qui intercepte le même arc qu’un des angles intérieurs demandés.
Exemple :
On cherche la mesure de l’angle intérieur
de l’hexagone
régulier IJKLMN de centre O.
Dans le cercle C , l’angle
intercepte le même arc
que l’angle au centre
.
Or, dans un cercle, si un angle inscrit intercepte un
même arc qu’un angle au centre, alors la mesure de cet
angle inscrit est égale à la moitié de la mesure de cet
angle au centre.
Donc
=
Or,
est formé par les couples d’angles adjacents
;
,
;
et
;
.
Donc
=
+
+
+
= 60° + 60° + 60° + 60° d’après la propriété précédente d’où
= 240°.
Ainsi,
=
°
c’est-à-dire
=120°
L’angle
mesure 120°.
C
1
/
2
100%