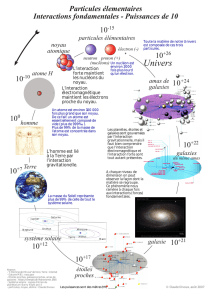
Principes de la cosmologie QUE HNI TEC

ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
Principes de la cosmologie
James Rich
T
Y
L
PO
N
H
EC
E
U
IQ
Adaptation française : Jean-Louis Basdevant
ÉDITION
ES
NIQ E
U
H
LE
S
D E L'É C O
ÉC
E
L
O
Y
L
PO
•L
ÉC
E
L
O
P O LY T E C
H
C
TE
U
Q
I
N
E
ÉC
E
L
O
ÉC
E
U
IQ
Ce logo a pour objet d’alerter le lecteur sur la menace que représente
pour l’avenir de l’écrit, tout particulièrement dans le domaine universitaire, le développement massif du «photocopillage».
Cette pratique qui s’est généralisée, notamment dans les établissements
d’enseignement, provoque une baisse brutale des achats de livres, au
point que la possibilité même pour les auteurs de créer des œuvres nouvelles et de les faire éditer correctement est aujourd’hui menacée. Nous
rappelons donc que la production et la vente sans autorisation, ainsi
que le recel, sont passibles de poursuites.
Les demandes d’autorisation de photocopier doivent être adressées à
l’éditeur ou au Centre français d’exploitation du droit de copie :
20, rue des Grands-Augustins , 75006 Paris. Tél. : 01 44 07 47 70.
T
Y
L
PO
E
L
O
ÉC
N
H
EC
T
Y
L
PO
E
L
O
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
© Éditions de l’École polytechnique - Septembre 2004
91128 Palaiseau Cedex
U
Q
I
N
E
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
C
ÉPréface
Ce livre est destiné aux étudiants et chercheurs qui souhaitent comprendre la
physique de la cosmologie standard du « big-bang » ainsi que l’interprétation des
observations les plus récentes. Il repose sur des cours que j’ai donnés depuis huit ans
à des étudiants de DEA de l’Université de Paris et à des élèves de troisième année de
l’École polytechnique. Comme la plupart de ces étudiants n’avaient pas l’intention de
devenir des cosmologistes professionnels, j’ai mis l’accent sur des sujets qui devraient
être d’un intérêt assez général.
T
Y
L
PO
N
H
EC
E
U
IQ
Dans les dix dernières années, la cosmologie observationnelle a enregistré des progrès stupéﬁants, et l’existence d’un nouvel ouvrage sur le sujet pourrait se justiﬁer
simplement par le fait de rendre compte de toutes ces avancées. Les succès traditionnels de la cosmologie moderne sont bien connus. Les plus importants sont la
compréhension dynamique de l’expansion universelle, la prévision et l’observation du
rayonnement de fond cosmologique et le calcul des abondances des éléments légers.
À cela, on doit ajouter les nouvelles observations qui laissent à penser que nous entrons dans une ère de « cosmologie de précision ». L’observation la plus spectaculaire
a peut-être eu lieu cette année avec la mise en évidence du premier pic acoustique
dans le spectre des anisotropies du rayonnement de fond cosmologique par les collaborations Boomerang et Maxima. Ces très belles mesures ont convaincu beaucoup de
physiciens que l’univers a une densité d’énergie proche de la valeur critique et qu’une
compréhension complète de la formation des structures est peut-être à portée de main.
ÉC
E
L
O
Si beaucoup de cosmologistes s’attendaient à une densité critique, l’observation
qu’elle se scinde en des composantes diﬀérentes a des implications révolutionnaires.
Les observations faites au cours de la dernière décennie ont conﬁrmé que la plupart
de la matière qui est liée dans les galaxies ou dans les amas de galaxies est d’une
espèce inconnue. Beaucoup de cosmologistes pensent que ces observations indiquent
qu’il existe de la « matière noire froide », probablement sous la forme de gaz d’une
particule massive interagissant faiblement, restée jusqu’ici non détectée directement.
La matière noire froide fait partie des meubles dans le circuit des conférences depuis
une vingtaine d’années, et l’on a tendance à oublier combien cette prévision est hardie.
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
Encore plus révolutionnaire est la conclusion, reposant sur les ﬂux observés provenant de supernovae de grand redshift, que l’expansion de l’univers est en train de
s’accélérer. Dans le cadre de la théorie gravitationnelle standard, cela implique que
ÉC
3
E
4
T
Y
L
PO
N
H
EC
E
U
IQ
Préface
le contenu en énergie de l’univers est dominé par une énergie eﬀective du vide ou, de
façon équivalente, par une constante cosmologique. Comme il s’agit d’une nouvelle
forme d’énergie qui n’est pas associée à une particule élémentaire, cette découverte, si
elle se conﬁrme, serait sur le même plan, du point de vue de son importance théorique,
que la découverte des champs électromagnétiques, par exemple.
ÉC
E
L
O
Les observations de la décennie à venir vont procurer des tests de précision de
cette représentation d’un univers dominé par de la matière noire froide et de l’énergie
du vide. Un problème plus diﬃcile sera de déterminer si ces deux substances sont des
« éléments de la réalité » ou simplement des éléments de théories. Même si l’Univers se comporte comme un univers régi par la relativité générale avec un mélange
de matière noire froide et d’énergie du vide, il se peut fort bien que la Nature nous
ait joué un tour à cause de notre ignorance sur un ingrédient clé. Il se pourrait par
exemple, qu’un modèle utilisant seulement de la matière ordinaire mais avec une sorte
de « gravitation modiﬁée » qui agirait aux échelles cosmologiques, reproduise également les observations. Certains auteurs ont mis en avant que cette idée provient
de ce que les modèles qui utilisent la forme la plus simple de particules de matière
noire froide ne prévoient pas correctement la structure des cœurs galactiques, ni le
nombre de petites galaxies. Le temps dira si ces objections au modèle standard se
maintiennent. Si elles le font, la situation risque de se compliquer. Nous devrons alors
nous reposer sur les observations cosmologiques pour déterminer les véritables lois de
la gravitation. Il serait certainement plus reposant que quelqu’un règle la question
directement en détectant les particules de matière noire.
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
Étant donné les questions fascinantes que soulève la cosmologie et l’intérêt suscité
par d’ambitieux programmes observationnels, on n’est pas surpris que certains étudiant souhaitent étudier le sujet avant de maîtriser complètement les fondements de
l’astronomie et de l’astrophysique observationnelles, de la physique des particules, de
la physique nucléaire et de la relativité générale. Ce livre tente de faire ainsi.
La relativité générale est sans nul doute l’aspect le plus diﬃcile de la théorie de la
cosmologie, et elle représente un formidable déﬁ pédagogique dans un cours d’introduction. Initialement, j’avais utilisé les démonstrations newtoniennes habituelles de
l’équation de Friedmann, mais c’est au bout du compte très insatisfaisant. J’ai ﬁni
par adopter la stratégie de présenter la gravitation relativiste nécessaire au problème
considéré en n’utilisant que les outils mathématiques indispensables à la cosmologie
dans son état présent. C’est faisable en raison de l’extrême simplicité de la cosmologie homogène. Nous obtiendrons tous les résultats intéressants sans faire appel aux
connexions aﬃnes ou aux dérivées covariantes.
H
C
TE
U
Q
I
N
Tout en essayant d’être « correct » au plan relativiste, j’ai adopté un point de vue
complètement phénoménologique sur la relativité générale, où la mathématique ne
s’éloigne jamais des observations faites avec des horloges et des radars. Par exemple,
les coordonnées comobiles sont déﬁnies de façon opérationnelle avant que l’on ne
découvre la métrique de Robertson–Walker à partir de considérations de symétrie
générales. Cette stratégie s’attaque à ce qui apparaît, à tort ou à raison, comme l’une
ÉC
E
L
O
Y
L
PO
E
Préface
T
Y
L
PO
N
H
EC
E
U
IQ
5
des grandes diﬃcultés de la pédagogie de la relativité générale, c’est-à-dire faire le
rapport entre tous les symboles et les mesures.
Dans le même esprit phénoménologique, dans un chapitre, on abandonne les coordonnées comobiles habituelles pour utiliser un système simple qui peut être construit
de façon opérationnelle par un observateur en chute libre. Dans un tel système de coordonnées, la métrique est localement Lorentzienne, et bien des choses qui sont obscures
ou mystérieuses dans les coordonnées comobiles deviennent relativement claires. Il est
notamment facile de démontrer l’équation de Friedmann, et la nature de la mystérieuse énergie du vide devient au moins plausible.
ÉC
E
L
O
Pour ce qui concerne la physique des particules et la physique nucléaire, j’ai surtout adopté le point de vue que ces disciplines existent principalement pour fournir au
cosmologiste une liste de particules connues ou hypothétiques, avec leurs interactions
et la valeur de leurs sections eﬃcaces. Par conséquent je n’ai pas tenté de faire la
moindre introduction à ces deux sujets fascinants. Des questions spéculatives comme
la matière noire supersymétrique et les champs scalaires inﬂationnaires ou de quintessence ne sont traités que phénoménologiquement, et je ne mentionne que brièvement
la diﬃculté que l’on peut rencontrer pour les intégrer dans une théorie cohérente des
particules élémentaires.
T
Y
L
PO
N
H
EC
E
U
IQ
Enﬁn, pour ce qui est de l’astronomie et de l’astrophysique, j’ai essayé de fournir
les éléments minimaux pour pouvoir comprendre les observations. Les mesures sont
souvent présentées sous une forme assez non-digérée de façon que les étudiants puissent ressentir la qualité des données et la diﬃculté de les analyser. Je mets souvent
l’accent sur l’importance des hypothèses utilisées dans l’interprétation des données
astrophysiques, souvent ambiguës.
ÉC
E
L
O
Je ne suis pas remonté des données aux moyens observationnels. Cela signiﬁe que
je n’ai pas présenté dans le détail mérité les progrès technologiques importants qui ont
rendu ces observations possibles. Parmi ceux-ci, mentionnons la nouvelle génération
des télescopes de classe 10 m et le Hubble Space Telescope qui ont fourni une vision
tellement plus claire des objets lointains. Les télescopes spatiaux à rayons X ont permis d’étudier en détail les amas de galaxies, les plus gros objets liés de l’univers. Tous
ces télescopes ont fourni des quantités considérables de données de haute qualité en
raison des progrès dans la technologie de détection des photons. Les plus évidents sont
les nouvelles caméras CCD qui ont peu à peu remplacé les plaques photographiques.
Les grandes mosaïques de CCD ont permis de découvrir les supernovae de grand redshift, elles ont permis d’eﬀectuer des explorations de redshifts considérables, ainsi que
la cartographie des distributions de masse par eﬀet de lentille gravitationnelle. Mentionnons également les nouveaux bolomètres cryogéniques qui ont été utilisés dans les
mesures de Boomerang et de Maxima, et qui pourront peut-être un jour permettre la
détection des particules de matière noire.
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
Je n’ai pas pu, non plus, parler des techniques de simulation numérique qui sont
si importantes dans la compréhension de la formation des structures. La discussion
de ce type de processus sera donc assez qualitative.
ÉC
E
6
T
Y
L
PO
N
H
EC
E
U
IQ
Préface
Je n’ai pas abordé le problème non-résolu de comment est initiée la formation
d’étoiles, qui crée ainsi l’univers visible des galaxies. Jusqu’à ce que les astronomes
parviennent à déterminer complètement la distribution de matière dans l’Univers à
l’aide de l’eﬀet de lentille gravitationnelle, ce problème continuera de troubler l’étude
des structures qui repose sur le comptage des galaxies visibles.
ÉC
E
L
O
En ﬁn de compte, je n’ai pas fait de revue de l’historique de la cosmologie moderne. Cette histoire commence avec la découverte par Hubble de l’expansion universelle et son interprétation par Lemaître. Elle a été suivie par la théorie de Gamow de
la nucléosynthèse primordiale et la prévision de l’existence du fond de rayonnement
cosmologique, conﬁrmé expérimentalement par Penzias et Wilson en 1965. Cette histoire est maintenant bien connue et je n’y ferai plus allusion. Une conséquence est que
les travaux des pionniers ont été un peu négligés par rapport aux travaux plus récents.
E
U
IQ
Plusieurs personnes ont contribué à ce travail. Les plus importantes sont mes étudiants au DEA de Champs, Matière et Particules et au DEA de Physique Théorique.
Les questions qu’ils m’ont posées aussi bien que les questions que je pensais qu’ils
pourraient poser ont été pour moi une constante stimulation. Je remercie particulièrement l’étudiante (anonyme) qui m’a lancé un regard furieux lorsque je lui ai dit que
si elle voulait comprendre l’origine de l’équation de Friedmann, elle devait suivre un
cours de relativité générale. Les chapitres 3 et 4 de ce livre son nés de ce moment tendu.
T
Y
L
PO
N
H
EC
Ce livre n’existerait pas sans les encouragements, les conseils et l’aide de JeanLouis Basdevant. Il m’a suggéré d’essayer mon cours de DEA sur les élèves de l’École
polytechnique, dans un enseignement optionnel de second cycle de « Majeure ». Cette
expérience m’a forcé à clariﬁer une bonne partie de la physique de base. Il m’a ensuite poussé à transformer mon cours en un livre. Par ailleurs, je lui dois cette version
française de l’ouvrage original : « Fundamentals of Cosmology » paru chez SpringerVerlag en mai 2001. J’épargne au lecteur les merveilleuses discussions linguistiques
(et autres) que nous avons eues. Il me dit qu’il apprend beaucoup sur la physique
et sur l’anglais en parlant avec moi, c’est réciproque (de toute façon, nous sommes
incapables de dire dans quelle langue, anglais ou français, nous nous parlons ; nos
élèves en sont témoins).
ÉC
E
L
O
Les personnes suivantes ont lu tout ou partie du manuscrit et m’ont fait d’importantes suggestions : Alexis Amadon, Jean-Louis Basdevant, Guillaume Blanc, Alain
Blanchard, Jean-Francois Glicenstein, David Langlois, Thierry Lasserre, Alain Milsztajn, David Lloyd Owen, Charling Tao Dominique Yvon, et particulièrement Jacques
Haissinski. Ils ont trouvé de nombreuses erreurs (pas toutes !) et m’ont très aimablement fait remarquer certains passages par suﬃsamment clairs.
H
C
TE
U
Q
I
N
J’ai bénéﬁcié de discussions avec de nombreux collègues sur l’état de la recherche
récente. J’adresse des remerciements tout particuliers à Monique Arnaud, Christophe
Balland, Marc Besancon, Pierre Binétruy, Alain Blanchard, Jim Bartlett, Nathalie
Deruelle, Ken Ganga, Andy Gould, David Graﬀ, Michael Joyce, Boris Kayser, David
Langlois, Christophe Magneville, Alain Milsztajn, Yannick Mellier, Robert Mochkovitch, Reynald Pain, Marguerite Pierre, Joe Silk, Alfred Vidal-Madjar, Michel Spiro,
ÉC
E
L
O
Y
L
PO
E
Préface
T
Y
L
PO
N
H
EC
E
U
IQ
7
Elizabeth Vangioni-Flan, et tous ceux que j’oublie dans cette liste.
Des ﬁgures non encore publiées m’ont été données par Monique Arnaud, Ken
Ganga, Thierry Lasserre, et Elizabeth Flan-Vangioni. Merci à Albert Bosma pour
avoir fait ressusciter la ﬁgure 2.25. J’ai reçu l’aimable autorisation de reproduire des
ﬁgures provenant du web par l’European Southern Observatory, la NASA et le COBE
working group, l’Agence Spatiale Européenne et le Supernova Cosmology Project.
ÉC
E
L
O
James Rich
Gif-sur-Yvette, Avril, 2002
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
E
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
ÉC
N
H
EC
T
Y
L
PO
E
L
O
E
U
IQ
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
E
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
C
des matières
ÉTable
1 Introduction
1
Composition de l’univers . . . . . . . . . . . . . . . . . .
1.1
L’univers visible : les galaxies . . . . . . . . . . .
1.2
Baryons . . . . . . . . . . . . . . . . . . . . . . .
1.3
Matière noire froide (CDM) . . . . . . . . . . . .
1.4
Photons . . . . . . . . . . . . . . . . . . . . . . .
1.5
Neutrinos . . . . . . . . . . . . . . . . . . . . . .
1.6
Le vide . . . . . . . . . . . . . . . . . . . . . . .
2
L’évolution de l’univers . . . . . . . . . . . . . . . . . .
2.1
Le paramètre d’échelle a(t) . . . . . . . . . . . .
2.2
La gravitation et l’équation de Friedmann . . . .
2.3
Univers ouverts et fermés . . . . . . . . . . . . .
2.4
Évolution de la température . . . . . . . . . . . .
2.5
Une équation de Friedmann améliorée . . . . . .
2.6
L’Évolution des Ω et la Formation des Structures
2.7
Le scénario standard . . . . . . . . . . . . . . . .
3
Questions en suspens . . . . . . . . . . . . . . . . . . . .
Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
13
14
14
24
25
27
27
31
32
32
33
37
39
44
46
49
51
56
2 Cosmologie observationnelle
1
Étoiles et quasi-étoiles . . . . . . .
2
Galaxies . . . . . . . . . . . . . . .
3
Amas de galaxies . . . . . . . . . .
4
La matière noire . . . . . . . . . .
4.1
Les wimps . . . . . . . . . .
4.2
Les axions . . . . . . . . . .
4.3
Matière noire baryonique .
5
Les paramètres cosmologiques . . .
5.1
H0 . . . . . . . . . . . . . .
5.2
Les diverses densités ρ et Ω
Exercices . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
57
57
72
76
81
81
85
85
91
91
94
99
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
N
H
EC
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Y
L
PO
9
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
E
U
IQ
H
C
TE
U
Q
I
N
E
10
E
U
IQ
Table des matières
T
Y
L
PO
N
H
EC
3 Coordonnées et métriques
1
Relativité et gravitation . . . . . . . . . . .
2
Coordonnées comobiles . . . . . . . . . . . .
3
La métrique I : surtout l’isotropie . . . . . .
4
La métrique II : surtout l’homogénéité . . .
5
Propagation des photons . . . . . . . . . . .
6
Distance de luminosité et distance angulaire
7
L’équation des géodésiques . . . . . . . . .
8
Eﬀet de lentille gravitationnelle . . . . . . .
Exercices . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
113
116
123
126
130
134
137
140
143
151
4 Les équations du champ gravitationnel
1
Nos coordonnées en chute libre . . . . .
2
Le tenseur énergie-impulsion . . . . . . .
3
L’équation de Friedmann . . . . . . . .
4
Les paramètres cosmologiques . . . . . .
5
Champs scalaires . . . . . . . . . . . . .
6
Le tenseur de Riemann . . . . . . . . . .
7
Un univers avec ρ = 0 . . . . . . . . . .
8
Le tenseur d’Einstein . . . . . . . . . . .
9
L’équation d’Einstein générale . . . . . .
Exercices . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
159
160
164
169
171
173
175
179
180
181
185
5 Applications de l’équation de Friedmann
1
L’âge de l’univers . . . . . . . . . . . . . . . . .
2
Distances de luminosité et distances angulaires
3
Le problème de l’horizon . . . . . . . . . . . . .
4
Le problème des Ω . . . . . . . . . . . . . . . .
5
L’inﬂation . . . . . . . . . . . . . . . . . . . .
6
Diﬀusion et absorption intergalactique . . . . .
Exercices . . . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
189
191
195
202
210
212
214
216
ÉC
E
L
O
ÉC
E
L
O
T
Y
L
PO
6 L’histoire thermique de l’univers
1
Distributions à l’équilibre . . . .
2
L’équation de Boltzmann . . . .
3
Électrons et positrons . . . . . .
4
Neutrinos . . . . . . . . . . . . .
5
La nucléosynthèse primordiale . .
6
Wimps . . . . . . . . . . . . . . .
7
Baryogénèse . . . . . . . . . . . .
8
L’irréversibilité . . . . . . . . . .
9
Le futur . . . . . . . . . . . . . .
ÉC
E
L
O
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
N
H
EC
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Y
L
PO
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
E
U
IQ
.
.
.
.
.
.
.
.
.
U
Q
I
N
.
.
.
.
.
.
.
.
.
H
C
TE
221
224
229
234
241
243
252
255
256
258
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
E
Table des matières
T
Y
L
PO
N
H
EC
E
U
IQ
11
Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 260
7 La formation des structures
1
Un modèle d’eﬀondrement sphérique .
1.1
La métrique . . . . . . . . . . .
1.2
Expansion et eﬀondrement . .
1.3
Le régime linéaire . . . . . . .
2
Le spectre des ﬂuctuations de densité .
3
Évolution newtonienne . . . . . . . . .
4
Entrée et sortie du rayon de Hubble .
5
Le spectre primordial . . . . . . . . . .
6
Modèles de matière noire froide . . . .
7
Neutrinos et baryons . . . . . . . . . .
8
Propagation des photons . . . . . . . .
9
Anisotropies du CBR . . . . . . . . . .
9.1
Les sources d’anisotropies . . .
9.2
∆θ > θH . . . . . . . . . . . .
9.3
∆θ < θH . . . . . . . . . . . .
9.4
Les paramètres cosmologiques .
Exercices . . . . . . . . . . . . . . . . . . .
ÉC
E
L
O
E
L
O
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
T
Y
L
PO
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
N
H
EC
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
267
273
274
275
280
282
289
294
298
303
306
308
312
314
317
318
321
323
E
U
IQ
A Vecteurs et tenseurs de Lorentz
329
B Unités naturelles
333
C Particules élémentaires
337
D Magnitudes
343
E Solutions des exercices
347
F Formules et nombres utiles
383
ÉC
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
ÉC
N
H
EC
T
Y
L
PO
E
L
O
E
U
IQ
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
E
T
Y
L
PO
N
H
EC
E
U
IQ
E
L
1
CO
ÉChapitre
Introduction
N
H
EC
E
U
IQ
La cosmologie est l’étude globale des caractéristiques de l’univers. Dans ses détails, le cosmos est complexe. Il comporte une multitude d’objets étonnants depuis les
molécules de fullerènes C60 jusqu’aux quasars. Les cosmologistes aiment à moyenner
sur ces objets et à considérer l’univers comme un endroit simple caractérisé par
T
Y
L
PO
– Une densité très faible, ρ ∼ 10−26 kg m−3 , et une émission lumineuse de J ∼
10−39 W m−3 ;
ÉC
E
L
O
– Une composition « chimique » curieuse (voir le Tableau 1.1). La plupart des
particules sont des photons ou des neutrinos froids alors que la majeure partie de
l’énergie est sous forme de matière ordinaire « baryonique » (protons, noyaux
et électrons), de matière noire et, selon toute apparence, une énergie eﬀective
du vide, que l’on nomme également constante cosmologique.
– Un état thermique hors d’équilibre caractérisé par des températures diﬀérentes
pour les photons et les neutrinos et un déﬁcit en noyaux fortement liés.
– Une hiérarchie de structures gravitationnellement liées, depuis les planètes et
les étoiles jusqu’aux galaxies et amas de galaxies.
Relevons enﬁn l’observation qui est à la base de la cosmologie moderne :
U
Q
I
N
– L’univers est en « expansion » en ce sens que la distance entre les galaxies
augmente avec le temps.
H
C
TE
Cette dernière observation implique que l’univers était plus dense dans le passé que
maintenant. Les faits observationnels ainsi que les lois de la physique qu’on ne peut
remettre en cause permettent d’aﬃrmer que l’expansion de l’univers se déroule depuis
une époque où la densité était supérieure de 40 ordres de grandeur à celle que nous
connaissons, avec une température de kT > 10 MeV. En remontant dans le temps,
nous pourrions voir les étoiles et les galaxies se fondre dans un plasma uniforme de
particules élémentaires.
ÉC
E
L
O
Y
L
PO
13
E
14
E
U
IQ
Chapitre 1. Introduction
T
Y
L
PO
N
H
EC
L’ambition première de la cosmologie est de déterminer l’état actuel, thermique,
chimique et structurel, de l’univers à partir des conditions qui régnaient dans l’univers
« primordial ».
Nous verrons dans le chapitre 6 que la composition chimique du tableau 1.1 ainsi
que le non-équilibre thermique s’expliquent en grande partie par les réactions qui
ont eu lieu à des températures voisines de 1 MeV. En particulier, nous calculerons
le rapport neutrino-photon nν /nγ avec grande précision, et nous verrons comment
le rapport hélium-hydrogène nHe /nH est directement lié au rapport baryon/photon
η = nb /nγ . Les autres rapports, parmi lesquels η lui-même, restent encore à expliquer.
La formation de structures, galaxies et amas de galaxies, dans l’univers n’est pas
encore bien comprise. Nous verrons toutefois dans le chapitre 7, le scénario standard
dans lequel les structures observées résultent de la croissance gravitationnelle de petites inhomogénéités dans l’univers primordial. L’incertitude dans ce secteur provient
actuellement de l’ignorance que nous avons sur la nature de la matière noire et sur
l’origine des inhomogénéités primordiales. Les idées les plus ambitieuses nous font
concevoir une époque « inﬂationnaire » qui s’est achevée lorsque l’univers était plus
dense d’un facteur ∼ 10120 que maintenant. Pendant la période inﬂationnaire, les inhomogénéités de densité seraient provenues des ﬂuctuations quantiques d’un champ
scalaire.
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
Dans ce chapitre d’introduction, nous allons commencer par faire une description
qualitative, dans la section 1, des divers composants du tableau 1.1. Dans la section 2,
nous introduirons le modèle cosmologique standard dans lequel l’évolution de l’univers
est déterminée par la gravitation au travers de l’équation de Friedmann, et par la
physique statistique au travers de l’équation de Boltzmann.
Les fondements observationnels du modèle standard seront présentés plus en détail au chapitre 2. Les aspects gravitationnels seront exposés au chapitres 3 et 4, ce
qui nous permettra, au chapitre 5, de comprendre comment l’on mesure les densités
cosmologiques. Les éléments de mécanique statistique nécessaires pour comprendre
l’évolution chimique de l’univers seront exposés au chapitre 6. Enﬁn, les éléments de
la théorie de la formation des structures seront introduits au chapitre 7. Tous ces
sujets sont exposés en plus grand détail dans les nombreux ouvrages sur l’astronomie
et l’astrophysique [2, 3], sur la relativité générale [7, 8], la physique des particules
élémentaires [9] et la cosmologie [13, 14, 15, 16, 17].
ÉC
1
1.1
E
L
O
Composition de l’univers
L’univers visible : les galaxies
Y
L
PO
H
C
TE
U
Q
I
N
Les « briques » de l’univers visible sont des galaxies (Figures 1.1 et 1.2) qui sont
elles-mêmes formées d’étoiles, de gaz interstellaire, et de matière noire non-identiﬁée.
Les galaxies sont de forme très variée (spirale, elliptique, irrégulière) tout comme le
sont leur masse et leur luminosité. Néanmoins, la majorité de la lumière produite dans
l’univers provient de galaxies comportant de 1010 à 1011 étoiles, ce qui produit une
ÉC
E
L
O
E
Composition de l’univers
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
15
Tab. 1.1: Les occupants recensés ou soupçonnés de l’univers. Pour chaque espèce, i, ce tableau donne la densité estimée des particules, ni , ainsi que l’estimation de la densité d’énergie
ou de masse, Ωi = ρi /ρc , normalisée à la « densité critique » ρc = 0.92 h270 × 10−26 kg m−3 .
Certaines des estimations dépendent de la valeur de la constante de Hubble H0 ce qui se
traduit par la présence de facteurs du type h70 = H0 /(70 km s−1 Mpc−1 ) ∼ 1. Sauf pour
la densité des photons, que l’on observe directement, tous les nombres dans ce tableau sont
évalués par des méthodes plus ou moins indirectes et doivent être maniés avec une certaine
précaution. Pour cette même raison, les barres d’erreurs ne doivent pas être prises comme
trop contraignantes.
ni (m−3 )
espèce
O
P
E
L
ÉCO
LY T
N
H
EC
E
U
IQ
Ωi = ρi /ρc
Référence
−5
Ωγ = 5.06 h−2
70 × 10
[21, 22]
−4
Ων > 4 h−2
70 × 10
[23]
photons du CBR
nγ = (4.11 ± 0.02) × 108
νe , νµ , ντ
nν = (3/11)nγ
(par espèce)
baryons
(+électrons)
nb ∼ 0.2 ± 0.05
(nHe /nH ∼ 0.08)
Ωb ∼ (0.04 ± 0.01) h−2
70
[24, 25]
matière noire
froide
?
ΩCDM ∼ 0.3 ± 0.1
[21]
« vide »
0
ΩΛ ∼ 0.7 ± 0.1
[26, 27, 25]
ΩT ∼ 1.1 ± 0.1
total
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
[25]
E
16
ÉC
E
U
IQ
Chapitre 1. Introduction
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
T
Y
L
PO
N
H
EC
E
U
IQ
Fig. 1.1: La galaxie spirale NGC1232 vue par le VLT de l’ESO. Avec la permission de
l’European Southern Observatory [28].
luminosité galactique de
Lgal ∼ 2 × 1010 L ,
(1.1)
où L est la luminosité du soleil, L = 2.4 × 1045 eV s−1 .
Les masses des galaxies ne sont pas bien déﬁnies car l’étude des vitesses de rotation
des nuages galactiques (voir section 2) montre que la plupart de la masse est contenue
dans des halos sombres, grosso modo sphériques, d’extension inconnue (ﬁgure 1.3). La
masse des régions visibles Mvis se trouve principalement dans les étoiles. On observe
qu’elle est à peu près proportionnelle à la luminosité galactique L. Le rapport « masseluminosité » typique est 4M par L
E
L
O
Y
L
PO
H
C
TE
Mvis /L ∼ 4 (M /L ) ,
ÉC
U
Q
I
N
(1.2)
où M = 1.988 × 1030 kg est la masse solaire. Cela entraîne une « masse visible »
E
Composition de l’univers
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
T
Y
L
PO
E
U
IQ
N
H
EC
17
E
U
IQ
Fig. 1.2: La Voie lactée vue de la Terre à 8 kpc du centre galactique. La ﬁgure est un image
de l’ensemble du ciel obtenue à partir de données provenant du Diﬀuse Infrared Background
Experiment (DIRBE) monté sur le Cosmic Background Explorer (COBE) dans les bandes
de longueur d’onde de 1.25, 2.2, et 3.5 micron. La plupart de l’émission à ces longueurs
d’onde provient d’étoiles K, comparativement froides et de faible masse, dans le disque et
dans le noyau de la Voie lactée. La poussière interstellaire n’obscurcit pas appréciablement
l’émission à ces longueurs d’onde ; les cartes représentent l’émission jusqu’aux extrémités de
la galaxie. Avec la permission de NASA Goddard Space Flight Center et du COBE Science
Working Group [29].
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
18
ÉC
E
U
IQ
Chapitre 1. Introduction
E
L
O
T
Y
L
PO
N
H
EC
dark halo
>50 kpc
10 kpc
T
Y
L
PO
N
H
EC
E
U
IQ
100 pc
disk
ÉC
E
L
O
bulge
Fig. 1.3: Une galaxie spirale typique vue par la tranche. La région visible a la forme d’un
disque de rayon ∼ 10 kpc et d’épaisseur ∼ 100 pc. On pense que la plus grande partie de la
masse est sous forme d’un « halo » sphérique dont on ignore l’étendue. La densité du halo
varie comme ρ ∝ R−2 si bien que la masse totale est proportionnelle au rayon R que l’on ne
connaît pas.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Composition de l’univers
T
Y
L
PO
typique par galaxie de
N
H
EC
E
U
IQ
Mvis ∼ 8 × 1010 M .
E
L
O
19
(1.3)
Le rayon des régions visibles des galaxies spirales est typiquement
ÉC
Rvis ∼ 10 kpc ,
(1.4)
où nous utilisons le « parsec », unité de distance communément employée en cosmologie : 1 pc = 3.26 années-lumière = 3.086 × 1016 m.
Les galaxies ne sont pas distribuées uniformément dans l’espace, ce qui provient de
leur interaction gravitationnelle. Les galaxies sont fréquemment regroupées dans des
amas liés, dont les plus grands contiennent des milliers de galaxies. En dépit de cette
inhomogénéité à « petite échelle », l’univers à grande échelle > 100 Mpc apparaît
comme uniforme avec un nombre volumique de galaxies visibles de
ngal ∼ 0.005 Mpc−3
N
H
EC
E
U
IQ
(1.5)
ce qui correspond à une distance typique intergalactique de ∼ 6 Mpc. Insistons sur
le fait que cette densité correspond à celle des galaxies « brillantes ». De fait, il
semble que le nombre volumique de galaxies diverge pour de faibles luminosités. Par
conséquent, le nombre total de galaxies est mal déﬁni. Ces petites galaxies contribuent
peu à la luminosité totale de l’univers :
ÉC
E
L
O
T
Y
L
PO
J ∼ Lgal ngal ∼ 108 L Mpc−3 .
(1.6)
La densité de masse totale correspondant à la partie visible des galaxies est
ρvis = JM/L ∼ 4 × 108 M Mpc−3
(1.7)
pour un rapport masse-luminosité de 4M /L .
La cosmologie moderne est née avec l’observation par Hubble que les galaxies
s’éloignent de nous avec une vitesse de récession dR/dt proportionnelle à leur distance
R (ﬁgure 1.4) :
dR
= H0 R + vp .
dt
U
Q
I
N
(1.8)
H
C
TE
Le facteur de proportionnalité H0 est appelé « constante de Hubble ». son inverse,
H0−1 , est le temps caractéristique pour que des changements appréciables de R se
produisent, et on peut considérer H0 comme le « taux d’expansion » actuel de l’univers local. La constante de Hubble ne doit pas être confondue avec le « paramètre de
Hubble » H(t) qui détermine l’évolution dans le temps du taux d’expansion1
E
L
O
Y
L
PO
1 La convention usuelle consiste à attribuer l’indice 0 à la valeur actuelle d’une grandeur cosmologique.
ÉC
E
20
ÉC
E
U
IQ
Chapitre 1. Introduction
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
T
Y
L
PO
N
H
EC
E
U
IQ
Fig. 1.4: Le « diagramme de Hubble » des vitesses de récession galactiques en fonction de
leur distance pour un ensemble d’amas de galaxies mesuré par le Hubble Key Project [30]. Les
vitesses sont déterminées par le redshift galactique et les distances sont évaluées par une série
de méthodes décrites au chapitre 2 en section 5.1. La pente de la droite donne la constante
de Hubble H0 .
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Composition de l’univers
T
Y
L
PO
N
H
EC
E
U
IQ
21
Comme indiqué en (1.8),, en plus de la « vitesse de Hubble » H0 R, les galaxies
possèdent des vitesses propres quasi-aléatoires que nous appelons vitesses « particulières » vp typiquement de l’ordre de vp ∼ 10−3 c ∼ 300 km s−1 .
La loi de Hubble (1.8) s’applique aux galaxies suﬃsammment « proches » pour
que v c. Dans ce cas, le temps de vol d’un photon entre la galaxie et nous est
suﬃsamment court pour que l’on puisse négliger la variation de R pendant le trajet.
Pour trouver la généralisation « relativiste » (3.59) de la loi de Hubble, applicable à
des galaxies plus lointaines, on doit être plus précis dans la déﬁnition de ce que l’on
nomme « distance », comme nous le verrons au chapitre 3.
Il est diﬃcile de mesurer la distance des galaxies. Pour cette raison, les estimations
de H0 ont varié de plus d’un ordre de grandeur depuis les travaux originaux de Hubble.
Les mesures les plus récentes [21] donnent des valeurs compatibles avec
ÉC
E
L
O
H0 = 70 ± 10 km s−1 Mpc−1 .
E
U
IQ
(1.9)
Dans la section 5.1 du chapitre 2 nous donnerons un aperçu des techniques qui mènent
à ces valeurs.
Puisque H0 est omniprésent dans les formules cosmologiques, il est utile de présenter les résultats numériques en introduisant le paramètre h = H0 /(100 km s−1 Mpc−1 ),
c’est-à-dire :
T
Y
L
PO
H0 = 100 h km s−1 Mpc−1
E
L
O
N
H
EC
h = 0.7 ± 0.1 .
(1.10)
Bien que h soit très largement utilisé dans la littérature nous préférons utiliser dans
ce livre h70 = H0 /(70 km s−1 Mpc−1 ) :
ÉC
H0 = 70 h70 km s−1 Mpc−1
h70 = 1.0 ± 0.15 ,
(1.11)
ce qui nolus permettra de donner des facteurs numériques correspondant directement
aux estimations actuelles de H0 .
Pour mesurer H0 , il est nécessaire de connaître les distances galactiques et les
vitesses de récession. Ces dernières sont aisément accessibles à partir du déplacement
vers le rouge, que nous nommerons dorénavant « redshift », des raies spectrales
galactiques
z ≡
λ0
−1,
λ1
U
Q
I
N
(1.12)
H
C
TE
où λ1 est la longueur d’onde du photon mesurée par un observateur au repos par
rapport à l’émetteur et λ0 est celle que nous observons. On peut interpréter le redshift
comme provenant de l’eﬀet Doppler2 de la vitesse de récession. Pour les galaxies
Y
L
PO
2 Le lecteur n’aimant pas l’interprétation Doppler ne doit pas s’inquiéter – ce n’est qu’une interprétation. Ce sont les relations entre quantités observables, les redshifts et les ﬂux de photons, qui
importent véritablement. En particulier, on observe que les galaxies peu lumineuses (car lointaines)
sont déplacées vers le rouge. C’est la relation entre le redshift et la luminosité apparente qui est
véritablement signiﬁcative. Nous établirons cette relation dans la section 5.
ÉC
E
L
O
E
22
E
U
IQ
Chapitre 1. Introduction
T
Y
L
PO
N
H
EC
proches, la vitesse de récession est nettement inférieure à la vitesse de la lumière, et
la formule de déplacement Doppler non relativiste (λ0 − λ1 )/λ1 = v/c signiﬁe
ÉC
E
L
O
z ∼ v/c
(v/c 1) .
(1.13)
En divisant (1.8) par c on voit que la loi de Hubble peut s’écrire
z =
H0
R
R + vp /c =
+ vp /c
c
dH
z1,
(1.14)
où dH est la « distance de Hubble » :
dH = cH0−1 = 3000h−1 Mpc = 4300 h−1
70 Mpc .
(1.15)
E
U
IQ
Il s’ensuit que z 1 si R dH . L’équation (1.14) permet d’estimer la distance d’une
galaxie à partir de son redshift, R ∼ zdH (z 1). Bien entendu, cette estimation
n’est valable que si la vitesse particulière est négligeable.
Dans ce livre, nous omettrons souvent d’écrire les facteurs « c » :
T
Y
L
PO
dH = H0−1 .
N
H
EC
(1.16)
C’est là le premier cas où nous faisons usage des « unités naturelles », système
d’unités où c, , et k sont « choisies » comme égales à 1. Comme nous le montrons
dans l’appendice B, on ne perd aucune information en négligeant les facteurs c et car on les retrouve aisément par analyse dimensionnelle.
ÉC
E
L
O
Il y a trois premières conséquences importantes de la loi de Hubble :
– L’univers est dynamique. Dans le passé, il était plus dense et, nous le verrons,
plus chaud. Des commentateurs imprudents aiment à extrapoler jusqu’à un point
de densité inﬁnie, appelé « big bang » ou « singularité primordiale ». Ce qui
est certain est que puisque nous ne connaissons pas les lois de la physique à
une densité supérieure à celle qu’avait l’univers avant 10−44 s , cette extrapolation ne peut pas être mise sous forme quantitative 3 . Notons cependant qu’en
extrapolant à partir des valeurs actuelles des vitesses de récession, un temps
de l’ordre de H0−1 s’est écoulé depuis cette singularité putative. Ce temps est
appelé « temps de Hubble » :
tH =
H0−1
10 −1
= 10 h
h−1
70
H
C
TE
an = 1.4 × 10
10
an .
U
Q
I
N
(1.17)
Dans le chapitre 5 nous verrons que le temps de Hubble est l’ordre de grandeur du temps écoulé depuis l’époque où s’appliquent « les lois de la physique
connues », c’est-à-dire depuis que la température était de l’ordre de ∼ 1 GeV.
E
L
O
Y
L
PO
3 Nous verrons que pour extrapoler, on doit connaître, entre autres, la pression en fonction de
la densité d’énergie. Nous ne possédons sur ce sujet aucun point de repère pour des températures
supérieures à ∼ 1 GeV.
ÉC
E
Composition de l’univers
T
Y
L
PO
N
H
EC
E
U
IQ
23
Notons également qu’en un temps de Hubble, la lumière peut parcourir une
distance ctH = dH , la distance de Hubble. On peut donc s’attendre à ce qu’il y
ait un « horizon » à la distance de Hubble. Au-delà de cet horizon, les objets
ne nous sont pas visibles car la lumière n’a pas eu le temps de nous parvenir.
Tout cela sera mis en forme au chapitre 5.
ÉC
E
L
O
– Comme on peut le constater sur la ﬁgure 1.5, la linéarité de la loi de Hubble
signiﬁe qu’un observateur dans une galaxie voisine voit une expansion universelle
avec la même constante H0 . Cela n’est vrai que si la relation entre vitesse de
récession et distance est linéaire. Toute autre loi impliquerait que nous occupons
une position privilégiée au « centre » de l’univers. Cela tend à faire penser que
l’univers est homogène dans notre voisinage dans le sens où tous les observateurs
dans diverses galaxies voient la même loi de Hubble et, très probablement, la
même densité de matière moyennée sur des volumes suﬃsamment grands. Que
cette homogénéité persiste au delà de l’horizon est une question intéressante
qui demeurera sans réponse pendant quelque temps encore. (L’horizon croît
avec un temps caratéristique tH .) Les cosmologistes ont, par tradition, souvent
supposé que l’univers tout entier est homogène, hypothèse élevée au rang de
« Principe cosmologique ». À l’heure actuelle, ce principe est peu-être démodé
car dans plusieurs théories, comme celle de l’inﬂation chaotique, l’univers est
très inhomogène à des échelles supérieures à l’horizon.
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
– À partir de H0 et de la constante de Newton G = GN , on peut former une
grandeur ayant la dimension d’une masse (ou d’une énergie) volumique appelée
« densité critique » :
ÉC
ρc =
3H02
= 0.92 h270 × 10−26 kg m−3
8πG
= 1.4 h270 × 1011 M Mpc−3 = 0.51 h270 × 1010 eV m−3 .
(1.18)
(1.19)
La seconde ligne montre que la densité critique correspond à une galaxie par
Mpc3 ou encore 5 protons/m3. S’il n’y a pas d’énergie du vide, l’expansion d’un
univers homogène super-critique s’arrête à un certain stade et se transforme en
une période de contraction qui se termine (si l’on ose extrapoler à une densité
inﬁnie) par un « big crunch». Dans le chapitre 4, nous verrons qu’un univers
homogène de densité super-critique a un volume ﬁni. S’il existe une énergie du
vide, cette corrélation entre la géométrie et le destin de l’univers est rompue,
mais ρc joue toujours le rôle d’unité « naturelle » de densité.
Y
L
PO
H
C
TE
U
Q
I
N
Il est commode de rapporter les densités cosmologiques à la densité critique et de
former des « Ω ». Par exemple, la densité totale moyenne ρT divisée par ρc est ΩT :
ÉC
E
L
O
ΩT ≡
ρT
.
ρc
(1.20)
E
24
E
U
IQ
Chapitre 1. Introduction
LY T
1
dR1
= H 0R1
dt
O
P
E
L
ÉCO
N
H
EC
d ( R1 - R2 )
= H 0 ( R1 - R2 )
dt
R1 - R2
R1
2
0
R2
dR2
= H 0 R2
dt
E
U
IQ
Fig. 1.5: Si un observateur dans la galaxie 0 voit une expansion universelle avec un taux
N
H
EC
H0 , un observateur dans la galaxie 1 ou 2 verra une expansion avec le même taux H0 . Cela
i
i /dt = H0 R
provient de ce qu’en négligeant les vitesse particulières, la loi de Hubble est dR
pour la position Ri de toute galaxie i. Cela entraîne que d(Ri − Rj )/dt = H0 (Ri − Rj ) pour
toute paire de galaxies i et j, ce qui signiﬁe que n’importe quelle galaxie peut être choisie
comme étant au « centre de l’univers ».
E
L
O
T
Y
L
PO
La densité de la matière visible (1.7) divisée par ρc donne
ÉC
Ωvis =
ρvis
∼ 0.003
ρc
(vis = ”visible” ∼ étoiles) .
(1.21)
On voit que s’il n’y avait que de la matière visible, l’univers serait sous-critique avec
ΩT ∼ 0.003.
Insistons sur le fait que les quantités notées « ρT », « ΩT » représentent les valeurs
actuelles. Les valeurs à d’autre époques seront notées « ρT (t) » et « ΩT (t) ». La densité critique dépend également du temps. Aﬁn d’éviter toute confusion, nous l’écrirons
explicitement 3H02 /8πG à l’époque actuelle et 3H(t)2 /8πG à d’autres époques.
1.2
Baryons
U
Q
I
N
On estime que la densité des baryons est supérieure d’un ordre de grandeur à celle
des baryons visibles (1.21) :
H
C
TE
Ωb = (0.04 ± 0.01) h−2
70 .
Y
L
PO
(1.22)
Cette estimation provient de la théorie de la nucléosynthèse des éléments légers [24]
qui permet de calculer correctement les abondances relatives des éléments légers si
Ωb est proche de cette valeur. En résumant brièvement les résultats du chapitre 6, la
composition nucléaire de l’univers change avec le temps au fur et à mesure que les
ÉC
E
L
O
E
Composition de l’univers
T
Y
L
PO
N
H
EC
E
U
IQ
25
étoiles transforment leur hydrogène en hélium, puis en éléments plus lourds. Néanmoins, il apparaît qu’il existe un mélange « primordial » de noyaux légers formé d’à
peu près 75% d’hydrogène (en masse) et de 25% 4 He accompagnés de traces de 2 H,
3
He, et 7 Li. Ce mélange est observé dans des régions qui n’ont pas été polluées par
la nucléosynthèse stellaire. Les abondances primordiales ont été déterminées par des
réactions nucléaires qui se sont produites lorsque la température de l’univers était de
∼ 60 keV. Les calculs de nucléosynthèse primordiale prévoient les abondances en fonction de la densité baryonique totale à T ∼ 60 keV, puisque cette densité détermine les
taux de réaction nucléaires. Nous verrons au chapitre 6 que les abondances calculées
correspondent aux abondances observées si la densité baryonique actuelle a la valeur
(1.22).
Puisque Ωb > Ωvis , on peut se poser la question de savoir où se trouvent les
baryons manquants, « noirs ». On pense que la plupart se trouvent dans le milieu
intergalactique sous forme d’un gaz ionisé [31]. Une fraction peut se trouver dans
des objets sombres compacts comme des étoiles mortes (étoiles à neutrons ou naines
blanches) ou dans des étoiles trop légères pour s’être allumées (des naines brunes).
Il a aussi été envisagé [32] qu’une fraction appréciable de baryons puisse se trouver
dans des nuages moléculaires froids.
En ﬁn de compte, mentionnons qu’il y a apparemment très peu d’antibaryons
dans l’univers visible [33]. Toute antimatière formée d’antibrayons et de positrons
s’annihilerait rapidement par collision avec de la matière ordinaire. Même si l’antimatière était séparée, d’une manière ou d’une autre, de la matière, les annihilations
dans l’espace integalactique à la frontière entre des domaines de matière et d’antimatière produirait un ﬂux de photons d’annihilation de haute énergie supérieur aux
ﬂus observé en provenance d’autres sources. Il semble probable par conséquent que la
densité d’antimatière est exponentiellement faible dans notre horizon (voir l’exercice
6.7).
ÉC
E
L
O
ÉC
1.3
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
Matière noire froide (CDM)
Les galaxies et les amas de galaxies ont été formées par eﬀondrement gravitationnel de matière non-relativiste. La théorie de ce processus sera évoquée au chapitre 7.
Un résultat central est qu’il est diﬃcile de comprendre comment une quantité (1.22)
de baryons pourrait avoir créé les structures observées. Le principal problème provient
de ce que les photons d’origine cosmologique (section 1.4) ont un spectre en énergie
pratiquement indépendant de la direction d’observation. Nous verrons que cela implique que la distribution des baryons était très homogène à des époques précoces.
Passer de cet état homogène à l’état inhomogène que nous connaissons à présent est
« diﬃcile » s’il n’y a que des baryons en raison de leur couplage étroit aux photons
qui, eux, ont une répartition très homogène.
Les modèles actuellement en vogue supposent qu’il existe de la matière noire sous
une forme qui n’a eu que des interactions faibles et qui a été non-relativiste depuis
l’époque où T était de l’ordre du MeV. Cette matière est appelée de façon générique
« matière noire froide ». Pour faciliter la lecture, nous conservons l’abbréviation
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
26
E
U
IQ
Chapitre 1. Introduction
T
Y
L
PO
N
H
EC
anglaise CDM (cold dark matter). On suppose fréquemment que cette matière est
formée de particules massives non-baryoniques interagissant faiblement, appelées génériquement des « wimps » (weakly interacting massive particles). Le fait qu’elles
aient des interactions faibles leur permet de graviter librement sans être contraintes
par l’interaction avec d’autres particules (baryons et photons).
ÉC
E
L
O
La densité actuelle de CDM est estimée être supérieure d’un ordre de grandeur à
celle des baryons, tout en restant en deçà de la densité critique
ΩCDM ∼ 0.3 .
(1.23)
On pense que la matière noire constitue la majeure partie de la masse des halos
galactiques et des amas de galaxies.
E
U
IQ
Malheureusement, il n’existe pas de wimp connu dans le zoo actuel des particules
élémentaires (Appendix C) et leur existence est une prévision hardie de la cosmologie.
Certaines extensions du modèle standard de la physique des particules élémentaires
prévoient l’existence de wimps suﬃsamment lourds pour ne pas avoir encore été détectés dans les accélérateurs. On a pu penser au début qu’un nouveau neutrino lourd
de masse mν > 1 GeV pouvait constituer la CDM, mais cette idée a été écartée [34]
au vu de la combinaison de résultats dans les accélérateurs et de recherches directes
(section 4).
ÉC
E
L
O
T
Y
L
PO
N
H
EC
Une classe de modèles plus hypothétiques qui prévoit l’existence de wimps est
constituée par les modèles « supersymétriques ». Dans ces modèles, chaque fermion
(resp. chaque boson) est apparié avec un partenaire supersymétrique qui est un boson
(resp. un fermion). Le partenaire supersymétrique le plus léger (LSP) est stable et ne
peut avoir que des interactions faibles, ce qui en fait un candidat idéal pour un wimp.
Au chapitre 6 nous verrons que les partenaires du modèle supersymétrique peuvent
être choisis de façon que le wimp ait la densité requise aujourd’hui (1.24). On estime
que la masse doit être comprise entre 10 GeV et 10 TeV. Des tentatives sont en cours
pour détecter les particules supersymétriques dans les accélérateurs aussi bien que
dans la galaxie (section 4).
D’autres candidats pour la matière noire non-baryonique sont des neutrinos légers et des trous noirs primordiaux. [35]. Nous verrons que des neutrinos de densité
(1.24) devraient avoir des masses de l’ordre de 10 eV. Comme nous le verrons dans
le chapitre 7, de telles particules légères auraient des diﬃcultés à former les structures observées. En eﬀet, elles auraient été relativistes lorsque la température était de
T ∼ MeV et formeraient ce qu’on appelle de la « matière noire chaude ». Les trous
noirs primordiaux conviennent bien pour ce qui concerne la formation de structures
mais il manque aux cosmologistes un scénario convaincant pour que ces trous noirs
soient produits en abondance dans l’univers primordial. [35].
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
La densité totale de matière non-relativiste est la somme des densités de CDM, de
baryons et de neutrinos massifs. Si les théories et estimations actuelles sont justes, la
ÉC
E
Composition de l’univers
T
Y
L
PO
N
H
EC
masse totale est dominée par la CDM, d’où
ΩM ∼ ΩCDM ∼ 0.3
E
L
O
4
E
U
IQ
27
:
(M = matière non − relativiste.)
(1.24)
Hormis les cas où la distinction est importante, nous ne nous préoccuperons pas de
diﬀérencier ΩCDM et ΩM .
É1.4C Photons
Les particules les plus abondantes dans l’univers sont les photons du fond cosmique, que nous notons CBR (cosmic background radiation) (également appelé « CMB »
dans la littérature : cosmic microwave background). Ces photons ont un spectre thermique presque parfait comme on peut le constater sur la ﬁgure 1.6. La température
des photons est Tγ = 2.725 Kelvin = 2.35 × 10−4 eV ce qui correspond à un nombre
volumique de nγ = 411cm−3 . Ce nombre est considérablement plus élevé que celui des
photons émis par les étoiles (exercice 2.2). En dépit de leur grande abondance, la faible
température des photons du fond cosmique résulte en une faible densité d’énergie :
N
H
EC
−5
.
Ωγ = 5.06 h−2
70 × 10
T
Y
L
PO
E
U
IQ
(1.25)
L’univers d’aujourd’hui est pratiquement transparent aux photons (exercice 2.3).
Au chapitre 6, nous verrons que les photons du CBR ont été thermalisés lorsque la
température était supérieure à 0.26 eV et que la matière baryonique était complètement ionisée. À T ∼ 0.26 eV, la matière baryonique s’est « recombinée » pour former
des atomes, et la décroissance correspondante de la section eﬃcace photon-matière a
rendu l’univers transparent.
La température du CBR n’est pas complètement isotrope. On constate des variations relatives de l’ordre de 10−5 d’une direction d’observation à l’autre. On pense que
ces petites variations proviennent des inhomogénéités de densité présentes au moment
de la recombinaison. Ces anisotropies de température fournissent des informations sur
les « conditions initiales » de la formation des structures. Comme nous le verrons au
chapitre 7, le spectre des anisotropies, interprété dans le cadre des modèles en vogue,
procure des informations qui, elles aussi, contraignent ΩT à être proche de 1.
ÉC
1.5
E
L
O
Neutrinos
U
Q
I
N
En sus des photons thermiques, on pense que l’univers est rempli de neutrinos,
νe , νµ et ντ ainsi que des anti-neutrinos correspondants. Les trois « saveurs » de
neutrinos correspondent aux neutrinos produits dans les interactions avec les leptons
chargés correspondants e, µ et τ . Par exemple, le νe est produit dans la désintégration
β en association avec un électron ou un positron :
Y
L
PO
H
C
TE
(A, Z) → (A, Z ∓ 1) e± νe (ν̄e ) .
E
L
O
(1.26)
4 Malheureusement, il n’existe pas dans la littérature de notation standard pour les Ω, et « Ω »
0
est utilisé pour noter tantôt ΩM tantôt ΩT .
ÉC
E
28
ÉC
E
U
IQ
Chapitre 1. Introduction
E
L
O
T
Y
L
PO
10
10−17
N
H
EC
Wavelength (cm)
1.0
0.1
Iν (W m−2 sr−1 Hz−1)
10−18
10−19
2.73 K blackbody
10−20
ÉC
10−21
10−22
N
H
EC
E
U
IQ
E
L
O
T
Y
L
PO
1
FIRAS
DMR
UBC
LBL-Italy
Princeton
Cyanogen
COBE satellite
COBE satellite
sounding rocket
White Mt. & South Pole
ground & balloon
optical
10
100
Frequency (GHz)
1000
Fig. 1.6: Spectre observé du rayonnement cosmique (CBR) [21]. Les points aux longueurs
d’onde < 1 cm proviennent d’observations terrestres. Aux longueurs d’onde plus courtes,
l’atmosphère terrestre est opaque et les mesures doivent être eﬀectuées en ballons, dans des
fusées ou dans des satellites. Les points de haute précision autour du pic du spectre ont été
obtenu avec le détecteur FIRAS du satellite COBE (1989-1995) [22]. Compilation due à The
Particle Data Group.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Composition de l’univers
T
Y
L
PO
N
H
EC
E
U
IQ
29
Le νµ est produit dans la désintégration du méson π en association avec un muon :
π ± → µ± νµ (ν̄µ ) .
E
L
O
(1.27)
Le ντ est produit dans la désintégration du τ :
ÉC
τ ± → π ± ν̄τ (ντ ) .
(1.28)
On pense que les neutrinos de « saveur » bien déﬁnie, νe , νµ et ντ , sont, en fait, des
combinaisons linéaires (au sens quantique) de neutrinos de masse bien déﬁnie ν1 , ν2
et ν3 :
νf =
3
αf i νi
(1.29)
i=1
E
U
IQ
pour f = e, µ, τ .
Les neutrinos interagissent encore plus faiblement que les photons du CBR mais
leur taux d’interaction à T > 1 MeV est suﬃsamment élevé pour qu’ils aient été
thermalisés. Au chapitre 6 nous verrons que pour des températures T < me , les
neutrinos relativistes ont une température légèrement inférieure à celle des photons :
ÉC
E
L
O
T
Y
L
PO
N
H
EC
Tν = (4/11)1/3 Tγ .
(1.30)
Cela correspond à une densité d’énergie par espèce de neutrino (+ antineutrino)
relativiste de
ρν = (7/8) × (4/11)4/3 ργ = 0.227 ργ
par espèce relativiste
(1.31)
et à un nombre volumique de neutrinos (+ antineutrinos) de
nν = (3/11)nγ
par espèce.
(1.32)
Cette relation est valable même si les neutrinos sont maintenant non-relativistes. Par
conséquent, on s’attend à nν = 112 cm−3 par espèce aujourd’hui.
Pour une espèce de neutrino de masse eﬀectivement nulle, mν Tν , la somme des
contributions des neutrinos et des antineutrinos de cette espèce à la densité d’énergie
est encore plus faible que celle des photons du CBR :
−5
Ων = 1.15 h−2
70 × 10
H
C
E
si mν 10−4 eV .
T
Y
POL
U
Q
I
N
(1.33)
Pour une espèce dont la masse est plus grande que la température calculée, les neutrinos sont maintenant non relativistes, et la somme des densités de neutrinos et
d’antineutrinos est
Ων =
E
L
O
mν
mν n ν
= 0.2 h−2
70
ρc
10 eV
ÉC
si mν 10−4 eV .
(1.34)
E
30
E
U
IQ
Chapitre 1. Introduction
T
Y
L
PO
N
H
EC
Si une espèce de neutrino possède une masse de l’ordre de quelques eV, elle doit
contribuer notablement à la densité d’énergie universelle. On peut aussi remarquer
que toute espèce de neutrino telle que nν ∼ nγ doit avoir une masse mν < 30 eV si
l’on veut éviter une densité cosmologique plus grande que celle que l’on observe.
Les limites sur les masses des neutrinos proviennent d’études cinématiques des
désintégrations (1.26), (1.27) et (1.28). Les limites actuelles [21] ne sont pas très
contraignantes : m1 < 10 eV, m2 < 170 keV et, m3 < 18.2 MeV, où i = 1, 2, 3 correspondent aux neutrinos de masses bien déﬁnie les plus proches, quantiquement, des
νe , νµ et ντ .
L’indication expérimentale de l’existence d’une masse non-nulle pour les neutrinos
provient de l’étude des « oscillations de neutrinos » c’est-à-dire la transformation
d’un neutrino de saveur donnée en un neutrino d’une autre saveur, par exemple
ÉC
E
L
O
π + → µ+ νµ ,
(1.35)
E
U
IQ
suivie d’une interaction dans laquelle ce neutrino agit comme ayant une saveur diﬀérente
N
H
EC
ν p → τ − (!) pπ + .
T
Y
L
PO
(1.36)
Ces expériences ne sont malheureusement sensibles qu’aux diﬀérences des carrés des
masses des neutrinos 5 . L’observation récente d’oscillations de neutrinos produits par
des interactions de rayons cosmiques dans l’atmosphère [23] a donnée des résultats
dont l’interprétation simple est
ÉC
E
L
O
m23 − m22 ∼ 10−3 eV 2 .
(1.37)
Des anomalies dans le spectre des neutrinos solaires [36] peuvent s’expliquer par
m22 − m21 ∼ 10−5 eV2 .
(1.38)
Si ces résultats sont conﬁrmés, ils impliquent qu’il existe au moins deux
neutrinos non-relativistes. Les diﬀérences de masses ne donnent que des
férieures sur les masses elles-mêmes, en supposant que celles-ci sont très
les unes des autres m3 m2 m1 . Dans ce cas, on obtient m3 >
m2 > 0.002eV . Cela implique :
Ων > 0.0004 h−2
70 .
espèces de
limites indiﬀérentes
0.02eV et
(1.39)
U
Q
I
N
On pense généralement que les neutrinos ont une hiérarchie de masses semblable à
celle des leptons chargés. Si c’est le cas, les inégalités ci-dessus deviennent en bonne approximation des égalités. Il n’est pas possible actuellement de vériﬁer cette hypothèse,
si bien qu’il est possible qu’un neutrino soit important du point de vue cosmologique
si les espèces de neutrinos ont des masses voisines.
Notons enﬁn qu’en raison de leurs très faibles interactions, il y a peu d’espoir de
détecter le fond cosmique des neutrinos [37].
E
L
O
Y
L
PO
H
C
TE
5 Cette diﬀérence détermine la « longueur d’oscillation », c’est-à-dire la distance caractéristique
parcourue par un neutrino avant qu’il n’interagisse comme un neutrino d’une autre saveur.
ÉC
E
Composition de l’univers
1.6
Le vide
T
Y
L
PO
N
H
EC
E
U
IQ
31
La découverte récente qui est probablement la plus surprenante est que l’univers
semble dominé par une « énergie du vide » ou encore «constante cosmologique» Λ :
ÉC
E
L
O
ΩΛ =
Λ
∼ 0.7
3H02
(1.40)
Par déﬁnition, l’énergie du vide est une énergie qui n’est pas associée à des particules
et qui n’est donc pas diluée par l’expansion de l’univers. Cela implique que la densité
d’énergie du vide est indépendante du temps, sauf si le vide n’est que métastable. La
valeur qu’implique ΩΛ = 0.7 est
ρV (t) ∼ 3 h270 × 109 eV m−3 .
(1.41)
E
U
IQ
Nous discuterons au chapitre 5 les arguments observationnels en faveur d’une telle
forme d’énergie. Ces observations concernent la luminosité apparente d’objets de
grand redshift qui indique si l’expansion universelle est en accélération ou en décélération (ce qu’on attendrait de la part de la gravitation usuelle). On constate que
l’expansion s’accélère et cela peut s’expliquer, comme nous le verrons au chapitre 4,
par une densité d’énergie du vide positive.
On ne peut pas utiliser la physique fondamentale actuelle pour calculer la valeur
de l’énergie du vide, bien que ce concept soit couramment utilisé dans les théories
de jauge modernes des particules élémentaires. On s’attend à ce que cette quantité
change avec la température d’une façon que l’on sait calculer lors de transitions de
phase, par exemple la transition de phase électro-faible à T ∼ 300 GeV lorsque les
bosons intermédiaires W ± et Z 0 deviennent massifs. Alors que l’énergie du vide ne
change pas dans la collisions de particules, et peut donc être ignorée dans les expériences habituelles, elle mène à des eﬀets observables comme l’eﬀet Casimir entre
conducteurs neutres. Malheureusement, toutes les grandeurs calculables qui font intervenir l’énergie du vide ne concernent que des diﬀérences de densités d’énergie et
nous n’avons pas de moyen sûr actuellement pour calculer les densités elles-mêmes.
Malgré le manque d’idées, l’existence d’une énergie du vide d’une valeur donnée
par (1.41) est particulièrement surprenante. En unités naturelles, une densité d’énergie
a la dimension de la quatrième puissance d’une masse. Par conséquent, une densité
d’énergie du vide peut être associée avec une échelle de masse M
ÉC
E
L
O
T
Y
L
PO
ρV ∼
N
H
EC
M4
.
(c)3
U
Q
I
N
(1.42)
H
C
TE
On peut être tenté d’utiliser comme échelle fondamentale la masse de Planck mpl =
(c5 /G)1/2 ∼ 1019 GeV ce qui donne ρV ∼ 3 × 10123 GeV m−3 . Ce nombre est trop
grand de 122 ordres de grandeur, ce qui doit constituer le record de la plus mauvaise
prévision qualitative de l’histoire de la physique. En fait, la densité (1.41) peut être
reliée à une échelle de masse de ∼ 10−3 eV qui n’est reliée à aucune autre échelle
connue en physique des particules, même si elle est proche de l’estimation des masses
des neutrinos.
ÉC
E
L
O
Y
L
PO
E
32
E
U
IQ
Chapitre 1. Introduction
T
Y
L
PO
N
H
EC
Le deuxième problème que pose une densité d’énergie (1.40) est qu’elle est comparable à la densité de matière ΩM ∼ 0.3. Or la densité de matière change lors de
l’expansion de l’univers alors que l’énergie du vide ne change pas. Ainsi, nous semblons
vivre à une époque particulière où les deux énergies sont comparables. Ce problème
sera discuté plus avant dans la section 3.
Notons enﬁn que du point de vue observationnel, il est parfaitement possible que
l’énergie du vide varie lentement avec le temps au lieu d’être strictement constante. Ce
type de composante pourrait être associé à un champ scalaire hypothétique. Les modèles de «Quintessence» qui font intervenir ce type de champ font l’objet de multiples
discussions dans la littérature [38]. Ils reposent sur les problèmes mentionnés ci-dessus
concernant une énergie du vide pure, mais aucun modèle complètement satisfaisant
n’existe à l’heure actuelle.
ÉC
E
L
O
2
2.1
L’évolution de l’univers
Le paramètre d’échelle a(t)
T
Y
L
PO
N
H
EC
E
U
IQ
Il est commode de paramétriser l’expansion de l’univers par une fonction du temps
proportionnelle à la distance entre les galaxies. Cette fonction est appelée le «paramètre d’échelle» a(t) :
E
L
O
a(t) ∝ distances intergalactiques .
ÉC
(1.43)
La loi de Hubble dit que la dérivée logarithmique de a(t) est, à l’heure actuelle, égale
à H0 :
ï ò
ȧ
= H0
t0 ≡ aujourd hui .
(1.44)
a t0
Le nombre volumique de galaxies ngal est proportionnel à une distance−3 . Par
conséquent, si le nombre de galaxies ne change pas au cours du temps, la déﬁnition
(1.43) peut être remplacée par
Å
ã
ngal (t0 ) 1/3
a0 ≡ a(t0 ) .
(1.45)
a(t) ≡ a0
ngal (t)
U
Q
I
N
Alors que le nombre de galaxies n’est pas strictement constant (il n’y en avait
aucune au début) les limites actuelles sur la durée de vie du proton (τp > 1032 an)
font que le nombre baryonique est conservé avec grande précision. Il est donc encore
plus signiﬁcatif de déﬁnir a(t) à partir du nombre volumique moyen de baryons :
Å
ã1/3
nb (t0 )
.
(1.46)
a(t) ≡ a0
nb (t)
E
L
O
Y
L
PO
H
C
TE
À l’époque actuelle, il y a peu d’antibaryons dans l’univers observable et on peut
considérer que nb est le nombre volumique de baryons. Dans l’univers primordial, à des
ÉC
E
L’évolution de l’univers
T
Y
L
PO
N
H
EC
E
U
IQ
33
températures T > GeV, des antibaryons étaient présents sous forme d’un plasma de
quarks et d’antiquarks. À cette époque, nb est le nombre volumique baryonique, c’està-dire le nombre volumique de baryons moins le nombre volumique d’antibaryons.
La valeur actuelle du paramètre d’échelle a0 est, dans la plupart des applications,
une constante arbitraire qui a la dimension d’une longueur. Pour cette raison, nous
utiliserons le «paramètre d’échelle réduit» sans dimension
ÉC
E
L
O
â(t) ≡
a(t)
a0
(1.47)
Cependant, dans certains calculs concernant des objets de grand redshift, nous
aurons besoin du paramètre d’échelle dimensionné. Au chapitre 4 nous utiliserons une
déﬁnition à partir de la distance de Hubble dH = H0−1 :
dH
H −1
= .
a0 = 0
|1 − ΩT |
|1 − ΩT |
N
H
EC
E
U
IQ
(1.48)
Nous verrons au chapitre 3 que la singularité à ΩT = 1 ne pose pas de problème.
Le paramètre d’échelle jouera un rôle essentiel au chapitre 3 lorsque nous déﬁnirons
des coordonnées « comobiles ». Comme on peut le voir sur la ﬁgure 1.7, si l’on néglige
les vitesses particulières, la distance Ri (t) entre nous et la galaxie i est proportionnelle
à a(t) :
ÉC
E
L
O
T
Y
L
PO
Ri = a(t) χi .
(1.49)
La constante de proportionnalité χi est indépendante du temps. on l’appelle la coordonnée radiale « comobile » de la galaxie.
L’évolution temporelle des densités d’énergie dans l’univers s’exprime simplement
à partir du paramètre d’échelle. La densité ρM (t) associée à des particules nonrelativistes est proportionnelle au nombre volumique de particules. Il s’ensuit que
Å
ã
a0 3
ρM (t) = ρM (t0 )
= ρM (t0 ) â−3 .
(1.50)
a(t)
La dépendance en temps des densités d’autres types d’énergie sera donnée dans les
sections suivantes.
2.2
La gravitation et l’équation de Friedmann
H
C
TE
U
Q
I
N
En l’absence de gravitation, la vitesse de récession des galaxies serait constante,
ce qui impliquerait que ä = 0. En présence des eﬀets attractifs de la gravitation, on
s’attend à ce que l’expansion soit décélérée ä < 0. Nous ferons usage de la relativité
générale au chapitre 4 pour établir l’équation d’évolution de ä. Dans cette section,
en guise d’introduction, nous allons utiliser un argument newtonien (d’une validité
discutable) pour établir une équation qui, au bout du compte, se révélera correcte
dans un univers dominé par de la matière non-relativiste.
ÉC
E
L
O
Y
L
PO
E
34
ÉC
E
U
IQ
Chapitre 1. Introduction
E
L
O
T
Y
L
PO
N
H
EC
1
2
R 1 = a(t) χ 1
R 2 = a(t) χ 2
0
R 4 = a(t) χ 4
R3 = a(t) χ 3
E
U
IQ
4
3
T
Y
L
PO
N
H
EC
Fig. 1.7: Si l’on néglige les vitesses particulières, la distance Ri entre nous (galaxie 0) et la
galaxie i est donnée par Ri = a(t) χi où χi est indépendant du temps. La quantité χi est la
coordonnée radiale « comobile » de la galaxie i.
ÉC
E
L
O
Considérons la situation de la ﬁgure 1.8, on place une galaxie de masse m à une
distance R = χa(t) du « centre » d’un univers de densité uniforme ρ. Puisque la
distribution de masse est à symétrie sphérique, le théorème de Gauss « suggère » que
la galaxie subit une force dirigée vers l’origine et proportionnelle à la masse totale
contenue dans une sphère de rayon < χa(t) autour de l’origine :
|F | =
GM (χ)m
,
χ2 a 2
(1.51)
où
M (χ) = 4π(χa)3 ρ/3 .
(1.52)
U
Q
I
N
(Nous ne nous préoccupons pas du fait que le théorème de Gauss s’applique ou non
dans un milieu inﬁni.) En utilisant |F | = mR̈ = mχä on trouve l’équation de décélération de l’univers :
ä
−4πGρ
=
a
3
E
L
O
Y
L
PO
H
C
TE
si ρ ∼ ρM .
(1.53)
C’est la bonne équation si ρ est dominé par de la matière non-relativiste. (En généralisant cela au cas relativiste, nous verrons au chapitre 4 que le paramètre ρ dans
(1.53) est remplacé par ρ + 3p où p est la pression.)
ÉC
E
L’évolution de l’univers
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
35
.
|v| = χ a
F =
GM( χ)m
(χ a(t))2
.
T = m( χ a)2/2
E
U
IQ
U = −GmM( χ )/ χ a
HN
3
M( χ) = ρ 4π( χ a) /3
O
P
E
L
ÉCO
C
E
T
LY
χ a(t)
Fig. 1.8: Traitement newtonien de l’expansion de l’univers. Une galaxie de masse m est
placée dans un univers de densité uniforme ρ à une distance χa(t) du « centre de l’univers ».
La symétrie sphérique suggère que la force newtonienne exercée sur la galaxie est dirigée vers
l’origine et a une valeur F = GM (χ)m/(χa(t))2 , où M (χ) est la masse totale contenue dans
une sphère de rayon < χa(t) autour de l’origine. Pour une densité de masse uniforme ρ,
M (χ) = 4π(χa)3 ρ/3.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
36
E
U
IQ
Chapitre 1. Introduction
N
H
EC
Multipliant et divisant le membre de droite de (1.53) par H02 on trouve la valeur
actuelle de la décélération :
ï ò
ΩM
ä
si ρ ∼ ρM .
= −H02
(1.54)
a t0
2
ÉC
E
L
O
T
Y
L
PO
(Dans la généralisation relativiste, le facteur ΩM /2 est remplacé par (ΩM /2 − ΩΛ )).
Le temps caractéristique pour qu’il se produise un changement appréciable dans la
vitesse de récession est (ä/ȧ)−1 qui vaut aujourd’hui 2tH /ΩM si l’univers est dominé
par de la matière non-relativiste.
On trouve la solution ȧ(t) de (1.53) en tenant compte de ce que, pour un univers
dominé par de la matière non-relativiste, ρa3 est indépendant du temps. Dans ce cas,
on vériﬁe aisément que la solution est :
ò
ï
8πGρa3
2
a−1 + const.
ȧ =
3
N
H
EC
E
U
IQ
où la quantité entre crochets est indépendante du temps. Pour évaluer la quantité
entre crochets, on utilise les valeurs actuelles ȧ(t0 ) = H0 a0 et 8πGρ(t0 )/3 = H02 ΩT ,
et l’on obtient
ȧ
ÉC
E
L
O
2
T
Y
L
PO
8πGρa2
+ H02 a20 (1 − ΩT ) .
=
3
(1.55)
En divisant (1.55) par a2 on trouve l’ « équation de Friedmann » :
Å ã2
ȧ
8πGρ
= H02 (1 − ΩT ) â−2 .
−
a
3
(1.56)
Bien que (1.53) s’applique à une univers dominé par de la matière non-relativiste,
nous verrons au chapitre 4 que l’équation de Friedmann (1.56) est complètement
générale pour un univers homogène.
L’équation (1.55) peut se lire comme la conservation de l’énergie de la galaxie de
la ﬁgure 1.8 :
8πGρa2
T +U
= ȧ2 −
= a20 H02 (1 − ΩT ) ,
2
mχ /2
3
où l’énergie cinétique T de la galaxie est
T =
Y
L
PO
et son énergie potentielle gravitationnelle U est
E
L
O
U (χ) = −
ÉC
H
C
TE
1
1
mṘ2 = mχ2 ȧ2 ,
2
2
8πGρa2
GmM (χ)
= −
mχ2 /2 .
χa(t)
3
(1.57)
U
Q
I
N
(1.58)
(1.59)
E
L’évolution de l’univers
T
Y
L
PO
N
H
EC
E
U
IQ
37
On voit que ΩT > 1 (ΩT < 1) correspond à une énergie totale négative (positive) par
galaxie.
Dans la section suivante, nous trouverons la solution a(t) de l’équation de Friedmann et, pour ce faire, nous aurons besoin de la forme explicite de ρ(t). Pour de la
matière non-relativiste, nous savons déjà que
ÉC
E
L
O
ρM (a) = ρM (a0 )â−3 = ΩM
3H02 −3
â .
8πG
Dans ce cas, l’équation de Friedmann devient
Å ã2
ȧ
= H02 ΩM â−3 + (1 − ΩT )â−2
a
(1.60)
si ΩT ∼ ΩM .
(1.61)
Sur cette expression, on voit explicitement que l’équation de Friedmann donne le
taux d’expansion (H(t) = ȧ/a) en fonction de sa valeur actuelle H0 . Le coeﬃcient de
proportionnalité dépend de ΩM = ΩT et du paramètre d’expansion réduit â.
2.3
Univers ouverts et fermés
T
Y
L
PO
N
H
EC
E
U
IQ
La solution a(t) de l’équation de Friedmann pour un univers homogène dominé
par de la matière (1.61) dépend de la valeur de ΩT ∼ ΩM . La ﬁgure 1.9 montre
trois exemples avec ΩT = ΩM ainsi que le modèle actuellement préféré avec (ΩM =
0.3, ΩΛ = 0.7). Deux classes peuvent être distinguées pour ΩT = ΩM suivant leur
comportement aux temps longs :
ÉC
E
L
O
– ΩT = ΩM ≤ 1. Dans ce cas, (1.61) montre que ȧ est positif quelque soit â.
Par suite, l’expansion se poursuit sans ﬁn. Cela ne suprend pas en raison de
ce que l’énergie newtonienne d’une galaxie (1.57) est positive pour ΩT < 1.
Un univers homogène avec ΩT < 1 est appelé univers « ouvert ». On possède
des expressions simples de a(t) dans deux cas. Pour un univers « vide » ΩT =
ΩM = 0, le premier terme du membre de droite de (1.61) est nul et l’on trouve
a(t) = a0
t
H0−1
(ΩT = ΩM = 0) .
(1.62)
L’âge de l’univers (le temps écoulé entre a = 0 et a = a0 ) est le temps de Hubble.
Pour un « univers critique » , ΩT = 1, le deuxième terme du membre de droite
de (1.61)) est nul et l’on obtient
Ç
a(t) = a0
t
(2/3)H0−1
å2/3
H
C
TE
(ΩT ∼ ΩM = 1) .
Y
L
PO
U
Q
I
N
(1.63)
L’âge de l’univers est les deux tiers du temps de Hubble. L’âge est inférieur au
cas ΩT = 0 car la gravitation a décéléré l’expansion. Par conséquent, l’expansion
était plus rapide dans le passé que maintenant et il a fallu moins de temps à
l’univers pour atteindre sa « taille » actuelle.
ÉC
E
L
O
E
38
ÉC
E
U
IQ
Chapitre 1. Introduction
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
T
Y
L
PO
N
H
EC
E
U
IQ
U
Q
I
N
Fig. 1.9: Le paramètre d’échelle a(t) pour quatre combinaisons de (ΩM , ΩΛ ). Les quatre
H
C
TE
courbes correspondent à la même valeur de a0 et H0 . Le temps écoulé entre la singularité
initiale et aujourd’hui (t0 ) est tH pour (ΩM = ΩΛ = 0), (2/3)tH pour (ΩM = 1, ΩΛ = 0),
0.58tH pour (ΩM = 2, ΩΛ = 0), et 0.96tH pour (ΩM = 0.3, ΩΛ = 0.7). Cette dernière
combinaison correspond au modèle actuellement à la mode qui repose sur l’observation de
supernovas à grand redshift et sur celle des anisotropies du CBR (Chapitre 2, Sec. 5).
ÉC
E
L
O
Y
L
PO
E
L’évolution de l’univers
T
Y
L
PO
N
H
EC
E
U
IQ
39
– ΩT = ΩM > 1. Le cas ΩT > 1 est appelé univers « fermé ». Pour ΩT = ΩM > 1
l’expansion s’arrête (ȧ = 0) lorsque a = amax :
ÉC
2.4
E
L
O
amax = a0
ΩM
ΩT − 1
(ΩT = ΩM > 1) .
(1.64)
Puisque ä < 0, l’expansion actuelle sera suivie par une phase de contraction
qui s’achèvera (peut-être) par un « big crunch ». Nous verrons au chapitre 3
qu’un univers fermé a un volume spatial ﬁni. La relation entre la géométrie
(volume ﬁni) et le destin (big crunch) ne vaut que si l’énergie du vide s’annule.
Dans le cas contraire, un univers fermé (ΩT > 1 ⇒ volume ﬁni) peut avoir une
expansion sans ﬁn.
Évolution de la température
E
U
IQ
Lorsque l’univers se dilate, la densité d’énergie de matière non-relativiste diminue comme ρM ∝ a−3 . Cela provient tout simplement de la dilution des particules,
n ∝ a−3 . Dans cette section nous allons voir que la densité d’énergie de la matière relativiste (photons et neutrinos de masse nulle) décroît comme ρR ∝ a−4 . La diﬀérence
entre ces deux types de comportement provient de ce qu’un observateur comobile voit
une distribution d’énergie du CBR déplacée vers le rouge par un facteur ∝ a−1 de
sorte que l’énergie moyenne des photons 6 décroît comme a−1 . Cet eﬀet se combine à
la dilution, nR ∝ a−3 , pour donner ρR ∝ a−4 .
Le redshift des photons du CBR photons n’est pas diﬀérent de celui des raies
spectrales qui mène à la loi de Hubble. Considérons deux galaxies distantes de dR.
Si l’univers est homogène, des observateurs dans chacune des galaxies voient la même
distribution des photons du CBR. Deux observateurs verront notamment le même
rapport entre l’énergie moyenne du CBR et l’énergie d’une transition atomique donnée produite dans des étoiles locales. Certains des photons stellaires et certains des
photons du CBR dans une galaxie se dirigent vers l’autre galaxie. Lorsque les photons stellaires d’une des galaxies rencontrent l’autre, ils sont observés avec un redshift
d’un facteur (1 − H0 dR/c). Puisqu’il n’y a pas de diﬀérence fondamentale entre les
photons stellaires et ceux du CBR, les photons du CBR doivent être déplacés vers le
rouge par le même facteur dE/E = −H0 dR/c. Puisque tous les photons sont déplacés
vers le rouge par le même facteur, les spectre garde une forme planckienne dont la
température décroît.
Le temps pour échanger des photons entre les deux galaxies est dt = dR/c si bien
que chaque observateur voit une température du CBR qui décroît avec le temps selon :
ÉC
E
L
O
T
Y
L
PO
dT
= −H0 dt
T
E
L
O
N
H
EC
Y
L
PO
⇒
H
C
TE
T
dT
= − ,
da
a
U
Q
I
N
(1.65)
6 Nous verrons que c’est en réalité l’impulsion qui subit un redshift et qu’un fond de particules
non-relativistes subit le même redshift de son impulsion. Toutefois, s’agissant de particules nonrelativistes, l’énergie cinétique est négligeable et l’on peut ignorer l’eﬀet dans le calcul de la densité
d’énergie.
ÉC
E
40
E
U
IQ
Chapitre 1. Introduction
T
Y
L
PO
N
H
EC
Où dans la deuxième expression nous faisons usage de H0 = ȧ/a à t0 . La solution de
cette équation est
ÉC
E
L
O
T (t) = T (t0 )
a0
.
a(t)
(1.66)
Il s’ensuit que dans le passé l’univers était plus chaud qu’actuellement et que dans
le futur il sera plus froid. Le fait que la distribution en impulsion est déplacée vers le
rouge de façon uniforme provient de ce qu’une distribution de Planck reste une distribution de Planck 7 . Ce fait remarquable explique pourquoi on observe aujourd’hui
une distribution thermique bien qu’il n’y ait pas de collisions thermalisantes. Comme
nous le verrons au chapitre 6, les photons ont acquis leur distribution de Planck à une
époque précoce de l’univers lorsque la densité et par conséquent le taux de collision
étaient élevés.
Puisque la densité d’énergie des photons est proportionnelle à T 4 , on a
ργ (a) = ργ (a0 ) â−4
N
H
EC
E
U
IQ
(1.67)
La densité totale de matière relativiste doit inclure les neutrinos relativistes (et toute
autre espèce qui est relativiste aux premiers instants). En incluant seulement les
neutrinos pour le passé pas trop lointain, et en utilisant (1.31) on trouve
T
Y
L
PO
ρR (a) = ργ (a0 ) â−4 [1 + 0.227NνR(a)] ,
E
L
O
(1.68)
où NνR (a) est le nombre d’espèces de neutrinos relativistes à l’époque a(t). La densité
actuelle de matière relativiste, normalisée à la densité critique actuelle est alors
ÉC
ΩR = Ωγ [1 + 0.227NνR(a0 )] ,
(1.69)
Puisque la densité de matière relativiste (1.60) est proportionnelle à a−3 alors
que celle de la matière non-relativiste (1.68) est proportionnelle à a−4 , la matière
relativiste doit prédominer pour a → 0. L’époque où les densités relativiste et nonrelativiste étaient égales est appelée « teq ». En supposant que tous les neutrinos
étaient relativistes à cette époque, on trouve
âeq = â(teq ) =
1.68Ωγ
0.85 × 10−4
∼
.
ΩM
ΩM h270
Cela donne une température à teq de
Teq = 2.8 ΩM h270 eV
T
Y
POL
H
C
E
(1.70)
U
Q
I
N
(1.71)
Si tous les neutrinos ont une masse plus faible que cette valeur Teq , la valeur de aeq
donnée par (1.70) est correcte. Nous utiliserons (1.70) comme valeur nominale de aeq .
E
L
O
7 Que la normalisation de la distribution demeure planckienne, c’est-à-dire n ∝ T 3 et ρ ∝ T 4
γ
γ
provient de la conservation du nombre de photons, nγ ∝ a−3 . Puisque T ∝ a−1 il vient que nγ ∝ T 3 ,
ce qui préserve la normalisation. Ce point délicat sera repris dans la discussion ci-dessous de l’équation
de Liouville.
ÉC
E
L’évolution de l’univers
T
Y
L
PO
N
H
EC
E
U
IQ
41
En anticipant sur le chapitre 3, notons que l’obtention du redshift de la température (1.66) s’applique également aux photons n’appartenant pas au CBR. Considérons
un photon d’énergie E1 emis à t1 par une galaxie lointaine et détectée sur Terre à t0 .
En utilisant le même raisonnement, l’énergie mesurée de ce photon est
ÉC
E
L
O
E0 = E(t1 )
a1
.
a0
(1.72)
Puisque la longueur d’onde d’un photon est inversement proportionnelle à son énergie,
on obtient une formule pour le redshift :
z+1 ≡
a0
λ0
=
.
λ1
a1
(1.73)
Cette formule élégante exprime que la longueur d’onde d’un photon se transforme par
le même facteur que l’univers lui-même8 . Nous donnerons une autre démonstration
de cette formule au chapitre 3 en utilisant des coordonnées co-mobiles.
Terminons cette section par une remarque formelle, non indispensable. La loi (1.66)
peut s’obtenir de façon plus formelle en faisant usage de « l’équation de Boltzmann »
qui régit la distribution de particules dans l’espace des phases
T
Y
L
PO
F =
E
L
O
dN
.
d3 r d3 p
N
H
EC
E
U
IQ
(1.74)
Nous considérons ici l’équation de Boltzmann pour des photons en l’absence d’interactions entre les particules, c’est-à-dire l’équation de Liouville. Cette approximation
est justiﬁée car l’univers est suﬃsamment dilué pour que les collisions entre photons
et matière soient très peu fréquentes (exercice 2.3). Au chapitre 6 nous donnerons une
démonstration de l’équation de Boltzmann avec collisions, ce qui permettra de traiter
l’univers dense primordial.
= 0) une distribution therAujourd’hui (t = t0 ) nous observons localement (R
mique de photons avec T (t0 ) = T0 ∼ 2.7 K. Cela correspond à une distribution de
t)
Planck dans l’espace des phases F (
p, R,
ÉC
= 0, t0 ) =
F (
p, R
1
1
(2π)3 exp(Ep /kT0 ) − 1
Å
1
c
ã3
.
(1.75)
U
Q
I
N
= 0) dans le
Nous voulons calculer la distribution dans l’espace des phases à (R
futur. Comme nous l’avons vu, les photons qui seront présents ici demain sont là-bas
aujourd’hui, ce qui signiﬁe que
H
C
TE
= −vp dt, t0 ) .
= 0, t0 + dt) ∝ F (
p, R
F (
p, R
Y
L
PO
(1.76)
8 C’est pourquoi certains disent que la longueur d’un photon croît parce que l’espace est en expansion. Bien que nous ne prétendions pas comprendre le sens de cette aﬃrmation, nous ne pouvons
aﬃrmer qu’il soit impossible de lui trouver un sens. Insistons cependant sur le fait que l’espace n’apparaît pas comme étant en expansion uniforme car la taille d’objets comme les atomes et les galaxies
ne croît pas avec le temps.
ÉC
E
L
O
E
42
T
Y
L
PO
px
ÉC
E
U
IQ
Chapitre 1. Introduction
E
L
O
N
H
EC
x
R
.......
.......
.dx
.
...
........................... dp
. .. . . x
....
.......
...........................
.........
.. . .
t
t+R/c
N
H
EC
E
U
IQ
Fig. 1.10: Photons dans l’espace des phases. La boîte sur la droite contient des photons avec
px < 0 et py = pz = 0 qui, au temps t, sont en (x ∼ R, y = z = 0). En suivant les trajectoires
individuelles, on voit qu’au temps t+R/c, les photons ont la même impulsion mais sont dans
une boîte située en x ∼ 0. La taille et la forme de la boîte ne changent pas car les photons
ont tous la même vitesse. Le fait que cette taille ne change pas implique que la densité dans
l’espace des phases ne change pas, c’est-à-dire que la constante de proportionnalité dans
(1.76) est égale à l’unité.
ÉC
E
L
O
T
Y
L
PO
L’impulsion p qui apparaît dans les deux membres de cette équation est l’impulsion
dans notre référentiel galiléen. En particulier, la quantité p dans le membre de droite
n’est pas l’impulsion p que mesurerait un observateur au repos dans une galaxie
= −vp dt. L’utilisation de référentiels galiléens sera justiﬁée
s’éloignant à la position R
au chapitre 4 où nous verrons que l’espace-temps peut être considéré comme plat sur
des échelles nettement inféreures à dH .
Sur la ﬁgure 1.10, on voit que la constante de proportionnalité dans (1.76) est
égale à l’unité (théorème de Liouville). Il s’ensuit que
∂F
RF .
= −vp · ∇
∂t
H
C
TE
U
Q
I
N
(1.77)
C’est là l’équation de Liouville en l’absence de forces. Les forces gravitationnelles
peuvent être négligées car le gradient du potentiel gravitationnel (1.59) s’annule à
l’origine. Une fois encore, la justiﬁcation relativiste de tout cela devra attendre le
chapitre 4.
dans notre référentiel galiléen sont reliés aux
Les impulsion des photons en dR
par une
impulsions mesurées par un observateur dans une galaxie en récession en dR
transformation de Lorentz avec β = H0 dR/c 1, c’est-à-dire p → p − Ep β. Il s’ensuit
ÉC
E
L
O
Y
L
PO
E
L’évolution de l’univers
px
T
Y
L
PO
x
ÉC
E
L
O
N
H
EC
E
U
IQ
px
x
t=0
dx
. .... ... .....
... . ..
.. ...
..... ............
(0,p)
43
t =0
dx [γ(1−β)]
dp x
(0, γ p (1+β) )
. .
.... .....
. .... .. .....
. . .. . .
... ... ... .
dp x [γ(1+β)]
N
H
EC
E
U
IQ
Fig. 1.11: Photons de py = pz = 0 et y = z = 0 vus dans deux référentiels reliés par une
transformation de Lorentz le long de l’axe x. Le fait que l’aire de la boîte soit la même dans
les deux référentiels entraîne que la constante de proportionnalité dans (1.79) est égale à
l’unité.
que
ÉC
E
L
O
T
Y
L
PO
0, t0 )
t0 ) ∝ G(
p − H0 Ep dR,
F (
p, dR,
(1.78)
où G(
p) est la distribution dans l’espace des phases vue par la galaxie en récession en
(qui correspond à l’origine dans son référentiel). Une fois encore, la constante de
dR
proportionnalité est égale à un (ﬁgure 1.11) car la transformation de Lorentz préserve
la densité dans l’espace des phases.
Si l’univers est homogène, la fonction G est la même que celle que nous observons
dans notre référentiel galiléen à l’origine. En faisant usage de cela, l’équation (1.78)
devient
0, t0 ) .
t0 ) = F (
p − H0 Ep dR,
F (
p, dR,
(1.79)
R F = −H0 Ep ∇
pF .
∇
U
Q
I
N
qui est équivalent à
En insérant cette expression dans (1.77) on obtient
Y
L
PO
H
C
TE
∂F
pF .
= H0 p·∇
∂t
En changeant de variables t → a(t) et en utilisant H0 = ȧ/a (t0 ), on obtient
ÉC
E
L
O
a
∂F
pF .
= −
p·∇
∂a
(1.80)
(1.81)
(1.82)
E
44
E
U
IQ
Chapitre 1. Introduction
T
Y
L
PO
La solution générale est
N
H
EC
F (
p, a) = F (pa/a0 , a0 ) ,
E
L
O
(1.83)
c’est-à-dire que l’impulsion des photons est déplacée vers le rouge d’un facteur a0 /a.
Une solution particulière est
ÉC
= 0, p
F (R
, a) =
1
1
,
(2π)3 exp(Ep /T (a)) − 1
(1.84)
avec
T (a) = T0
a0
.
a
(1.85)
L’évolution de nγ s’obtient en intégrant sur d3 p l’équation (1.82) ou sa solution
(1.83)
ȧ
dnγ (r = 0, t)
= −3 nγ
dt
a
2.5
⇒
HN
nγ = nγ (a0 )
C
E
T
LY
E
U
IQ
a 3
0
a
.
(1.86)
Une équation de Friedmann améliorée
O
P
E
L
ÉCO
On doit modiﬁer l’équation de Friedmann (1.61) aﬁn de tenir compte de l’énergie qui n’est pas sous forme de matière non-relativiste. Deux formes d’énergie sont
concernées. La première est celle de matière relativiste dont la densité d’énergie est
donnée par (1.68). Une seconde forme est de l’énergie du vide. Cette énergie n’est pas
diluée pendant l’expansion, on s’attend donc à ce que
ρV (a) = ρV (a0 ) =
3H02
ΩΛ .
8πG
(1.87)
Au chapitre 4 nous verrons qu’il suﬃt d’ajouter ces autres sources d’énergie à
l’équation de Friedmann (1.61). On obtient
Å ã2
ȧ
= H02 ΩM â−3 + ΩR â−4 + ΩΛ + (1 − ΩT )â−2 ,
a
où ΩT est la somme des Ω respectifs :
ΩT = ΩM + ΩR + ΩΛ .
H
C
TE
(1.88)
U
Q
I
N
(1.89)
L’eﬀet des quatre termes dans l’équation (1.88) apparaît plus clairement si l’on multiplie par a2 :
ȧ2 = H02 a20 ΩM â−1 + ΩR â−2 + ΩΛ â2 + (1 − ΩT ) .
(1.90)
E
L
O
Y
L
PO
On voit que l’eﬀet de la matière, relativiste ou non, est de décélérer l’univers : ȧ → ∞
pour â → 0, ce que l’on attend de la part de la gravitation habituelle. D’un autre
ÉC
E
L’évolution de l’univers
T
Y
L
PO
N
H
EC
E
U
IQ
45
côté, l’existence d’une énergie du vide positive a pour eﬀet d’accélérer l’expansion :
ȧ → ∞ pour â → ∞ si ΩΛ > 0. Cette observation se conﬁrme si nous diﬀérencions
(1.90) :
Å
ã
ΩM −2
â + ΩR â−3 − ΩΛ â .
ä = −H02 a0
(1.91)
2
ÉC
E
L
O
Il est utile de déﬁnir le « paramètre de décélération » q0 :
ï ò
aä
ΩM
− ΩΛ ,
=
q0 ≡ −
2
ȧ t0
2
(1.92)
où nous avons négligé ΩR ΩM . À partir des deux premières dérivées (1.90) et
(1.91) nous pouvons donner le développement de Taylor de a(t) qui est utile pour
(t − t0 ) tH = H0−1 .
ô
ñ
Å
ã
q0 t − t0 2
t − t0
a(t) = a0 1 +
−
+ .....
tH
2
tH
T
Y
L
PO
N
H
EC
E
U
IQ
Nous utiliserons cette expression au chapitre 5 dans l’analyse du ﬂux provenant de
galaxies lointaines.
À partir de la dépendance en â des quatre termes de (1.88), on s’aperçoit que
l’univers passe par une succession d’époques où chacun des termes est prédominant,
comme nous le résumons dans le Tableau 1.2.
Dans tous les cas, l’univers commence par une époque de « rayonnement » qui
se termine à teq et est suivie par l’époque de matière. La ﬁn de l’époque de matière
dépend des valeurs de ΩT and ΩΛ . Si ΩT > 1 et ΩΛ ∼ 0, l’expansion atteint un
maximum à
ÉC
E
L
O
amax = a0
ΩM
ΩT − 1
ΩT > 1 , Ω Λ ∼ 0 .
(1.93)
Dans ce cas, l’expansion est suivie d’une contraction et l’époque de matière cesse avec
l’apparition d’une nouvelle époque de rayonnement.
Si ΩT < 1 et ΩΛ ≥ 0, l’expansion se poursuit indéﬁniment et l’époque de matière
est suivie soit par une époque de « courbure » lorsque l’équation de Friedmann est
dominée par le terme (1−ΩT ), soit par l’époque du « vide » si l’équation de Friedmann
est dominée par le terme ΩΛ . Nous nommons le temps de la ﬁn de l’époque de matière
tcΛ .
Pour ΩT < 1 et ΩΛ ∼ 0, l’époque de matière est suivie par l’époque de courbure
qui est caractérisée par une expansion libre
a > acΛ = a0
ΩT
1 − ΩT
E
L
O
Y
L
PO
a(t) ∝ t
H
C
TE
U
Q
I
N
époque de courbure
L’expansion est « libre », a(t) ∝ t parce que la densité de matière n’est pas suﬃsante
pour décélérer l’univers.
ÉC
E
46
E
U
IQ
Chapitre 1. Introduction
T
Y
L
PO
N
H
EC
Tab. 1.2: Les époques d’un univers en expansion indéﬁnie. Pour aeq , nous supposons trois
espèces de neutrinos avec mν < 1 eV.
ÉC
E
L
O
époque
a(t)
rayonnement : â < âeq = 1.68Ωγ /ΩM
= 0.85 × 10−4 /(ΩM h270 )
a(t) ∝ t1/2
matière :
a(t) ∝ t2/3
aeq < a < âcΛ
courbure : a > âcΛ = ΩM /(1 − ΩT )
(si ΩΛ = 0)
a(t) ∝ t
E
L
O
N
H
EC
E
U
IQ
1/2
a(t) ∝ exp(H0 ΩΛ t)
vide : a > âcΛ = (ΩM /ΩΛ )1/3
(si ΩT = 1, ΩΛ > 0)
T
Y
L
PO
Pour ΩT ∼ 1 et ΩΛ > 0, l’époque de matière est suivie par l’époque du vide qui
se caractérise par une expansion exponentielle
ÉC
Å
â > acΛ = a0
ΩM
ΩΛ
ã1/3
1/2
a(t) ∝ exp(H0 ΩΛ t)
époque du vide
L’expansion a une dépendance en temps diﬀérente dans les époques de courbure
et du vide. Néanmoins, elle est comparable en pratique car, comme nous le verrons
dans la section suivante, la formation des structures s’arrête à tcΛ . Si les estimations
actuelles, ΩM ∼ 0.3 et ΩΛ ∼ 0.7, sont correctes, la formation de structures a cessé
depuis âcΛ = (0.3/0.7)1/3 ∼ 0.75. Si ces nombres sont erronés et que ΩM ∼ 0.3 et
ΩΛ = 0. alors la formation de structures a cessé depuis un certain temps puisque
âcΛ = 0.3/0.7 ∼ 0.42.
2.6
H
C
TE
U
Q
I
N
L’Évolution des Ω et la Formation des Structures
Y
L
PO
Les Ω sont déﬁnis à partir des valeurs actuelles des densités et du taux d’expansion :
E
L
O
Ωi ≡
ÉC
ρi (t0 )
3H02 /8πG
i = T, M, R, Λ..... .
(1.94)
E
L’évolution de l’univers
T
Y
L
PO
N
H
EC
E
U
IQ
47
Cette déﬁnition peut être généralisée pour donner les valeurs des Ω en fonction du
temps :
ρi (t)
Ωi (t) ≡
3(ȧ/a)2 /8πG
ÉC
E
L
O
i = T, M, R, Λ..... .
(1.95)
L’équation de Friedmann (1.88) donne le taux d’expansion dans le dénominateur. La
dépendance en temps des composantes de l’énergie est donnée par (1.60), (1.68) et
(1.87). Pendant l’époque de matière, on obtient
ΩT (a) ∼ ΩM (a) ∼
1
1+
1−ΩT
ΩM
â
aeq < a < acΛ .
(1.96)
On voit que ΩT (a) → 1 quand a → 0. On pouvait le prévoir directement à partir
de l’équation de Friedmann (1.88) puisque le terme de courbure proportionnel à (1 −
ΩT )â−2 devient négligeable par rapport à ΩM â−3 lorsque a → 0.
La ﬁnesse avec laquelle ΩT était proche de l’unité dans le passé est impressionnante. Au début de l’époque de matière, âeq ∼ 10−4 , ΩT (a) était à 10−4 de l’unité
(pour des valeurs raisonnables de (1 − ΩT )/ΩM ).
Pendant l’époque de rayonnement, ΩT continue d’être proche de l’unité pour a →
0:
E
L
O
T
Y
L
PO
ΩT (a) = ∼ 1 −
ÉC
N
H
EC
1 − ΩT (a0 ) 2
â
ΩR (a0 )
E
U
IQ
a < aeq .
(1.97)
À l’époque de la nucléosynthèse, â ∼ 10−9 , ΩT (a) était à 10−14 de l’unité.
Le fait que ΩT → 1 pour a → 0 est une conséquence toute simple de la conservation
de l’énergie Newtonienne (1.57). Cette relation équivaut à
U ,
ΩT = (1.98)
E−U
où l’énergie E = constante. Que −U → ∞ pour a → 0 demande que ΩT → 1.
Ce qui est plus étonnant est que ΩT (a) ait été suﬃsamment proche de un pour
pouvoir le demeurer pendant une période de durée ∼ tH ∼ 1010 an. Il est facile de
montrer que, si à l’époque t1 on a |ΩT (a1 ) − 1| = 1, ΩT va diﬀérer de 1 de façon
signiﬁcative après que l’univers se sera dilaté d’un facteur −1/n avec n = 2 (n = 1)
pour l’époque du rayonnement (de la matière). Si ΩT (a) avait diﬀéré signiﬁcativement
de 1 dans le passé lointain, ou bien l’univers aurait rapidement atteint une expansion
maximale puis se serait recontracté, ou bien il serait rapidement devenu dominé par la
courbure ou par le vide. Le fait que ΩT ait été suﬃsamment proche de un apparaît de
façon naturelle dans les modèles inﬂationnaires comme nous le verrons au chapitre 5.
La longue durée de l’époque de matière avec ΩM (a) ∼ ΩT (a) ∼ 1 est importante
car un simple argument newtonien montre que des structures gravitationnellement
liées ne peuvent se former à partir de petites ﬂuctuations de densités seulement lorsque
ΩM (a) ∼ ΩT (a) ∼ 1. L’argument est illustré sur la ﬁgure 1.12 où l’on voit un univers
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
48
ÉC
E
U
IQ
Chapitre 1. Introduction
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
ρ=ρc
ρ>ρc
ÉC
E
L
O
T
Y
L
PO
N
H
EC
Fig. 1.12: Formation de structures dans un univers avec ΩM = ΩT ∼ 1. Dans ce type
d’univers, une région sur-dense (ρ > ρc ) peut évoluer comme un mini-univers fermé. Cette
région se dilate jusqu’à un rayon maximum puis se détache de l’expansion universelle en se
contractant et en formant un objet lié gravitationnellement, alors que le reste de l’univers
poursuit son expansion. Dans un univers avec ΩM signiﬁcativement plus petit que un, une
petite sur-densité ne suﬃra pas à rendre la région surcritique et cette région subira une
expansion éternelle. Dans un univers avec ΩM signiﬁcativement plus grand que un, les régions
un peu sur-denses n’ont pas le temps de former des structures avant que l’univers, comme
un tout, cesse de se dilater et se recontracte.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
L’évolution de l’univers
T
Y
L
PO
N
H
EC
E
U
IQ
49
de densité moyenne critique. Parce que ΩT = 1, l’énergie moyenne newtonienne (1.57)
d’une particule dans cet univers est nulle, ce qui permet une expansion sans ﬁn.
L’univers contient une région avec une petite sur-densité ρ + δρ, δρ ρ. Dans cette
région, l’énergie potentielle d’une particule sera abaissée de telle façon que son énergie
totale devienne négative T (r) + U (r) < 0. Ainsi, des particules dans les régions surdenses ne vont participer à l’expansion que pendant une durée ﬁnie avant d’atteindre
une expansion maximale et de retomber sur elles-mêmes en formant une structure
gravitationnellement liée comme une galaxie, ou un amas de galaxies. Ce processus
sera étudié au chapitre 7.
Dans un univers sous-critique, une petite sur-densité ne suﬃra pas à rendre l’énergie d’une particule négative. Une région sur-dense continuera son expansion, à un
taux plus faible.
Dans un univers notablement sur-critique, une petite sur-densité n’aura pas le
temps de former une structure puisque l’univers dans son ensemble se recontracte
après quelques temps de Hubble.
Pour le futur, a → ∞, on montre facilement que ΩT (a) → 0 si ΩT < 0 et ΩΛ = 0.
D’un autre côté, en présence d’énergie du vide ΩΛ > 0 l’univers devient critique pour
les temps longs ΩT (a) = ΩΛ (a) → 1. Dans tous les cas, la formation de structures
cesse lorsque cesse la domination de la matière tcΛ . Ce n’est que si ΩM = ΩT = 1
que les structures de taille continuellement croissante vont continuer de se former.
Par exemple, si ΩM = ΩT = 1, notre groupe local de galaxies formera une structure
gravitationnellement liée à l’amas de la Vierge, notre voisin.
ÉC
2.7
E
L
O
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
Le C
scénario standard
É
Nous avons vu que, dans le modèle cosmologique standard, l’univers traverse une
succession d’époques lorsque il est dominé successivement par le rayonnement, par
la matière non relativiste, puis soit par la courbure, soit par l’énergie du vide. La
dépendance des densités d’énergie en fonction de la température est montrée sur la
ﬁgure 1.13.
Dans le Tableau 1.3, nous énumérons quelques événements de formation qui découlent de ce scénario. La physique connue et acceptée à l’heure actuelle permet de
suivre avec conﬁance la succession des événements qui se sont produits à partir de
T ∼ 1 GeV lorsque l’univers était une soupe quasi homogène de quarks, de gluons et
de leptons. Au fur et à mesure du refroidissement de l’univers, une succession d’états
liés est apparue : hadrons, noyaux, atomes et, ﬁnalement, les états gravitationnellement liés que sont les étoiles et les galaxies. Les dates de formation des états liés
sont appelées des « recombinaisons ». Lors de la recombinaison de formation des
atomes, l’univers est devenu eﬀectivement transparent aux photons. Étonnamment,
les atomes ne sont restés formés que pendant un temps relativement court, car ils ont
été « ré-ionisés » par les photons produits dans les premières étoiles et les premiers
quasars. Mais à cette date, l’univers était suﬃsamment dilué pour rester transparent
(exercise 2.3).
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
50
ÉC
E
U
IQ
Chapitre 1. Introduction
E
L
O
125
T
Y
L
PO
GUT epoch
ρR
Log ρ (eV m−3)
100
75
50
T
Y
L
PO
E
L
O
ρΛ
N
H
EC
E
U
IQ
nucleosynthesis
matter−radiation
equality
ρ
25
ÉC
N
H
EC
M
recombination
today
0
−25 25
20
15
10
5
0
−5
−10
LogT (eV)
Fig. 1.13: La densité d’énergie, de rayonnement et du vide en fonction de la température.
L’échelle de température commence à la valeur attendue pour la grande uniﬁcation soit ∼
1016 GeV. Nous supposons que les particules CDM ont des masses supérieures à ∼ 10 GeV
de telle façon que la courbe de ρM commence à 10 GeV.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Questions en suspens
T
Y
L
PO
N
H
EC
E
U
IQ
51
Nous devons ajouter que la nature du rayonnement a changé avec la température. Aujourd’hui, le rayonnement est formé de photons et de neutrinos légers. À des
températures T > me , des paires électron-positron pouvaient être produites. Nous
montrerons au chapitre 6 que ces paires étaient en équilibre thermique avec les photons et donnaient lieu à un spectre de corps noir semblable à celui des photons et
des neutrinos. En remontant le temps, chaque fois que la température a dépassé un
seuil de production particule-antiparticule une nouvelle composante de rayonnement
de corps noir s’est constituée. Pendant cette période, le nombre de particules et d’antiparticules était pratiquement le même. Le petit excès d’électrons et de baryons que
nous connaissons aujourd’hui provient du faible excédent (∼ 10−10 ) de particules par
rapport aux antiparticules lorsque T me .
Notons ﬁnalement que les deux premières époques du Tableau 1.3, celle de la
baryogénèse et celle de l’inﬂation, sont pour le moment des spéculations et font intervenir une physique qui n’est pas totalement comprise. L’existence de ces époques est
postulée aﬁn d’expliquer certains mystères du scénario standard, comme l’existence
de la légère asymétrie particule-antiparticule et l’origine des ﬂuctuations de densité
qui a mené à la formation des structures.
ÉC
3
E
L
O
T
Y
L
PO
Questions en suspens
E
L
O
N
H
EC
E
U
IQ
Le modèle cosmologique standard explique beaucoup de choses mais il porte en lui
suﬃsamment d’interrogations pour assurer que la cosmologie restera un sujet plein
d’intérêt pendant encore quelque temps. Nous énumérons ci-dessous quelques questions qui, pour le moment, restent sans réponse.
ÉC
1. Quelles sont les valeurs précises des paramètres cosmologiques : H0 , les Ω, et
quel est le spectre des inhomogénéités primordiales ?
2. De quoi est formée la matière noire ? Tant que cette question restera sans réponse, il subsistera un doute sur le fait que la cosmologie standard correspond
en quoi que ce soit à la réalité.
3. Quelle est la théorie correcte de la gravitation à grande échelle ? Dans tout ce
livre, nous ferons usage de la théorie standard de la gravitation newtonienne
et einsteinienne, alors qu’il n’existe pas de vériﬁcation directe de cette théorie
même à l’échelle galactique, sans parler des échelles cosmologiques.
U
Q
I
N
4. Est-ce que les « constantes fondamentales » de la physique sont réellement
constantes sur des échelles de temps cosmologiques ?
5. Que s’est il passé pour T > GeV ?
Y
L
PO
H
C
TE
6. Quelle physique détermine l’importance relative du rayonnement, de la matière
non-relativiste et de l’énergie du vide, et pourquoi vivons-nous à une époque où
les deux dernières sont comparables ?
E
L
O
Les questions 1 et 2 sont au cœur de l’observation cosmologique actuelle. Les
questions 3 et 4 sont des thèmes récurrents, à la limite de la spéculation cosmologique.
ÉC
E
52
ÉC
E
U
IQ
Chapitre 1. Introduction
E
L
O
T
Y
L
PO
N
H
EC
Tab. 1.3: Quelques événements-clés dans le passé. Les valeurs de t0 , trec , et teq dépendent
de (h70 , ΩM , ΩΛ ),nous utilisons ici (1, 0.3, 0.7).
t
Tγ (eV)
événement
t0 ∼ 1.5 × 1010 an
2.349 × 10−4
aujourd’hui
∼ 109 an
∼ 10−3
formation des premières structures,
réionisation atomique
trec ∼ 5 × 105 an
0.26
E
L
O
teq ∼ 5 × 104 an
ÉC
0.8
T
Y
L
PO
N
H
EC
E
U
IQ
« recombinaison » (formation d’atomes),
L’univers devient transparent
égalité matière-rayonnement
6 × 104
nucléosynthèse (formation des noyaux légers,
A = 2, 3, 4, 6, 7)
1s
106
e+ e− → γγ
4 × 10−6 s
∼ 4 × 108
transition de phase QCD (formation de
hadrons à partir des quarks et gluons)
< 4 × 10−6 s
> 109
baryogénèse ( ?) (génération de
l’asymétrie baryon-antibaryon)
3 min
U
Q
I
N
inﬂation ( ?)
(génération des ﬂuctuations de densité)
ÉC
E
L
O
Y
L
PO
H
C
TE
E
Questions en suspens
T
Y
L
PO
N
H
EC
E
U
IQ
53
Par exemple, un modèle de « gravitation newtonienne modiﬁée » faisant intervenir
une accélération fondamentale peut expliquer les courbes de rotation des galaxies sans
avoir à introduire l’existence de matière noire [40]. L’interrogation sur la variation
dans le temps des constantes fondamentales et ses implications cosmologiques a une
histoire longue et fascinante [41].
Les deux derniers points dans la liste ci-dessus sont des sujets importants au cœur
des spéculations actuelles sur la cosmologie. Nous allons les discuter plus complètement. S’agissant du point 5, il existe peu de points de repère expérimentaux pour
nous guider sur ce que peut être la cosmologie à des températures supérieures à
l’énergie des accélérateurs de particules actuels. Il est communément admis que les
idées essentielles de la théorie quantique des champs devraient rester valables jusqu’à
l’énergie de Planck, 1019 GeV, au delà de laquelle des eﬀets inconnus de gravitation
quantique deviendraient importants. On s’attend par conséquent à ce qu’en remontant le temps, la température de l’univers augmente, en franchissant de temps à autre
des seuils particule-antiparticule. Les particules qui sont présentes à ces hautes températures n’auront pas d’eﬀet signiﬁcatif sur le présent sauf si elles sont stables ou
si leurs interactions déterminent des nombres quantiques globaux, comme l’asymétrie
baryon-antibaryon.
Un exemple de ce que la prochaine génération d’accélérateurs peut révéler pour la
cosmologie est l’extension du modèle standard des particules élémentaires à la supersymétrie (voir Appendice C). Dans cette classe de théories, chaque fermion (boson) est
apparié à un nouveau boson (fermion). On s’attend en général à ce que les nouvelles
particules supersymétriques aient des masses dans la région 100 GeV < M < 10 TeV.
On s’attend aussi à ce que la particule supersymétrique la plus légère soit stable. Nous
verrons au chapitre 6 comment cette particule peut être produite thermiquement dans
les débuts de l’univers et comment on peut évaluer le « reliquat » de densité9 de ces
particules aujourd’hui. Il est naturel de supposer que ces particules constituent la
matière noire non-baryonique.
On pense également que les interactions de particules à des échelles supersymétriques jouent un rôle dans la génération de l’asymétrie baryon-antibaryon qui détermine le rapport baryon-photon actuel.
Au dessus des énergies supersymétriques se trouve l’échelle de « grande uniﬁcation » vers EGUT ∼ 1015 GeV. À cette énergie, les constantes de couplage eﬀectives
des interactions faibles, électromagnétiques et fortes convergent vers une valeur commune. On pense que des bosons super-lourds, dont les masses sont de cet ordre,
portent des interactions qui ne conservent pas le nombre baryonique, ce qui provoque
la désintégration du proton.
Du point de vue cosmologique, les interactions de GUT devraient produire des
objets « topologiquement » stables comme des monopôles magnétiques. La densité
attendue du reliquat de monopôles est très au dessus des limites observationnelles sur
ÉC
E
L
O
ÉC
E
L
O
9 Les
T
Y
L
PO
E
L
O
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
expressions anglaises du type « relic density » ou « relic baryons » etc. pour imagées qu’elles
soient, sont diﬃciles à transcrire même en franglais, puisque, pour certains, les reliques, comme les
fossiles, ont une valeur particulière. Nous nous en tenons, dans ce texte, à ce terme de reliquat qui
exprime très exactement la notion en question. Cela permet aussi d’éviter un problème grammatical.
ÉC
E
54
E
U
IQ
Chapitre 1. Introduction
T
Y
L
PO
N
H
EC
la densité actuelle de monopôles. Pour cette raison, l’inﬂation doit se produire à une
température inférieure à l’échelle GUT de façon à diminuer la densité de monopôles
au travers d’une expansion exponentielle de l’univers.
Tournons-nous maintenant vers la question cosmologique la plus intéressante :
celle de l’origine des valeurs relatives des densités du rayonnement, de la matière
non-relativiste, et de l’énergie du vide. Comme nous le verrons au chapitre 6, la
cosmologie explique avec succès l’abondance relative des éléments légers et le rapport
neutrino/photon. Le rapport baryon/photon η = nb /nγ ∼ 5×10−10 n’est pas expliqué,
pas plus que le rapport entre le nombre de particules CDM et le nombre de photons.
Commme nous le verrons au chapitre 6, on expère pouvoir calculer ces rapports lorsque
les paramètres fondamentaux de la physique des particules seront connus.
La situation est moins claire s’agissant de l’énergie du vide car les physiciens des
particules n’ont pas d’idée précise pour calculer ρV . La question a récemment pris
un tour nouveau avec la constatation que la densité eﬀective d’énergie du vide est
aujourd’hui comparable à celle de la densité d’énergie de matière Si l’on se reporte à la
ﬁgure 1.13, ce fait semble être une coïncidence extraordinaire puisqu’à l’époque GUT,
il y avait un écart d’environ 120 ordres de grandeur entre les densité du rayonnement
et du vide, alors qu’aujourd’hui les densités de matière et du vide ne diﬀèrent que
par un facteur ∼ 2. On peut s’interroger sur la possibilité que la physique à l’échelle
GUT ait pu eﬀectuer un ajustement si ﬁn (« ﬁne-tuning ») de ρV de façon telle
qu’il devienne comparable à la densité de matière exactement au moment où des
observateurs intelligents se mettraient à œuvrer.
En l’absence d’un consensus sur cette question, nous choisissons de prendre ce
problème de façon très générale. Cela va nous permettre de discuter de ce que nous
pouvons espérer apprendre au bout du compte sur la physique et la cosmologie. Deux
possibilités viennent à l’esprit pour expliquer la valeur de ρV :
ÉC
E
L
O
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
– La valeur actuelle de ρV est une quantité calculable dans le contexte de la physique des particules ou de sa généralisation (e.g. théorie des cordes ou gravitation
quantique)
– La valeur actuelle de ρV est une variable dynamique qui prend, dans l’espace
et dans le temps, des valeurs dans une plage qui dépend des « accidents » de
l’histoire. La physique fondamentale ne peut donner que la probabilité que telle
ou telle valeur soit observée.
U
Q
I
N
Les idées utilisées dans la première des hypothèses utilisent en général des champs
scalaires hypothétiques et sont appelées « modèles de quintessence ». Dans des modèles typiques de ce genre, l’énergie du champ commence, à des temps très précoces,
par être un peu plus faible que l’énergie du rayonnement. Les équations dynamiques
s’arrangent de telle façon que l’énergie du champ décroisse initialement avec le temps
en demeurant à une valeur relative constante par rapport à l’énergie du rayonnement.
À un certain instant critique, déterminé par la dynamique, l’énergie du champ adopte
une valeur constante. À partir de ce moment, elle se comporte comme une énergie
eﬀective du vide. En faisant en sorte que l’énergie du champ suive au début celle du
rayonnement, la diﬀérence surprenante de 120 ordres de grandeur entre énergie du
ÉC
E
L
O
Y
L
PO
H
C
TE
E
Questions en suspens
T
Y
L
PO
N
H
EC
E
U
IQ
55
rayonnement et énergie du vide peut être contournée. En choisissant la dynamique du
champ de manière ingénieuse (modèles de k-essence) [43], on peut s’arranger pour que
le champ devienne indépendent du temps à teq . Dans cette situation, il n’est pas étonnant que le champ se mette à dominer la densité totale d’énergie peu après, disons,
le moment présent. Bien entendu, le déﬁ, comme dans les modèles inﬂationnaires
de l’univers primordial, est de trouver un champ scalaire qui résolve les problèmes
cosmologiques tout en trouvant un bien-fondé du point de vue de la physique des
particules.
La seconde hypothèse est que ρV est une variable aléatoire. L’Astrophysique a de
nombreux exemples de telles situations, par exemple le rayon de l’orbite de la Terre. Il
peut sembler diﬃcile de concevoir une quantitié aussi « cosmologique » que l’énergie
du vide comme n’étant qu’une variable aléatoire. Il est utile d’imaginer que l’univers,
sur des échelles supérieures à l’horizon, est divisé en domaines dont l’énergie du vide
est diﬀérente. Cette idée n’a évidemment aucune implication observationnelle, mais il
est vrai que dans certaines théories, elle mène à des résultats conformes à la réalité.
Il faut également garder en tête que des grandeurs que nous considérons comme
étant calculables, comme l’abondance des éléments légers, dépendent en fait de la
valeur d’une série de constantes « fondamentales » dont l’origine est inconnue. Il
est parfaitement possible que certaines constantes fondamentales varient dans l’espace ou le temps sur des échelles suﬃsamment grandes et qu’une véritable théorie
fondamentale ne puisse donner que la probabilité qu’elles aient telle ou telle valeur.
Toutes les grandeurs qui ne peuvent être calculées physiquement qu’en probabilité
sont soumises au principe anthropique faible [44]. Nous voulons dire par là que, pour
calculer la probabilité d’observer une certaine valeur de la densité d’énergie du vide,
nous devons connaître non seulement la probabilité a priori P (ρV ) que se réalise une
certaine énergie du vide, mais également la probabilité que telle valeur de l’énergie
du vide permette l’apparition d’observateurs intelligents. Cela mène à une application
simple de la statistique de Bayes :
ÉC
E
L
O
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
P (d observer ρV ) ∝ P (ρV ) P (ρV ⇒ observateurs) .
(1.99)
Cela signiﬁe simplement que nous ne pouvons pas observer une valeur de l’énergie
du vide pour laquelle il est impossible que des observateurs apparaissent. Si l’énergie du vide varie sur des échelles supérieures à l’horizon, les observateurs existeront
préférentiellement dans les régions où la valeur de ρV est « bio-phile »10 . Mis à part
l’inconvénient qu’il ne soit pas possible d’obtenir d’information expérimentale sur ces
autres régions, cette aﬃrmation est la même que dire que le rayon de l’orbite terrestre est, en partie, déterminé par le fait que la température à cette valeur du rayon
est dans une plage de valeurs chimiquement intéressantes où une grande diversité
de molécules peuvent exister. Cela a résulté en un temps caractéristique d’évolution
des espèces vivantes bien inférieur sur Terre qu’il ne l’est sur les autres planètes du
système solaire.
10 Voire
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
« gnosophile » même si cette dernière contrainte est un « vaste programme ».
E
56
E
U
IQ
Chapitre 1. Introduction
T
Y
L
PO
N
H
EC
Les valeurs bio-philes de ρV peuvent être devinées simplement si l’on accepte de se
donner pour règle que la vie évolue préférentiellement dans les endroits où existent des
structures liées : atomes, molécules, planètes etc. Cela implique que la vie se développe
préférentiellement dans des domaines qui sont à une époque dominée par la matière. La
ﬁgure 1.13 nous dit alors que si ρV était supérieur de 12 ordres de grandeur à la valeur
observée, il n’y aurait pas eu d’époque dominée par la matière. Si l’on impose en outre
que l’époque dominée par la matière dure suﬃsamment longtemps pour que se forment
des objets gravitationnellement liés, on trouve une limite beaucoup plus contraignante.
À partir de l’observation du spectre des ﬂuctuations de densité primordiales (chapitre
7), les premières galaxies se sont formées à â ∼ 0.1. Si l’énergie du vide était 1000
fois supérieure à la valeur observée, elle aurait prédominé à â ∼ 0.1. La croissance
exponentielle de a(t) aurait empêché la formation de structures gravitationnellement
liées.
On voit que, sur une échelle logarithmique, ρV est proche de la limite supérieure de
la plage permise. Cela peut faire penser à une sorte de sélection anthropique combinée
à une probabilité a priori favorisant les grandes valeurs bio-phobes de ρV . On trouvera
un bon nombre de spéculation sur ce sujet dans la littérature [45].
Remarquons que la limite anthropique sur ρV dépend des autres paramètres cosmologiques. Considérons un univers ne contenant que des photons, des baryons et de
l’énergie du vide. Dans ce cas, l’égalité matière-rayonnement se produit à une température Teq ∼ ηmp où η = nb /nγ . L’égalité matièré-vide se produit à TcΛ = (ρV /ηmp )1/3 .
L’existence d’une époque dominée par la matière implique alors ρV < (ηmp )4 . L’application correcte de la statistique de Bayes à ρV dépend alors de ce que η soit une
quantité fondamentale ou une quantité anthropique. Dans les deux cas, une avancée
de la physique fondamentale est nécessaire, soit pour calculer la valeur fondamentale
de η, soit pour déterminer la loi de probabilité de η. Il était utile d’insister sur ce
point car on dit parfois que les gens invoquent le principe anthropique comme excuse
pour se permettre de faire des choses pas sérieuses.
ÉC
E
L
O
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
Exercices
1.1 Dessiner le graphe des fonctions ΩT (a), ΩM (a) et ΩΛ (a) dans le cas des valeurs
actuelles (ΩM = ΩT = 1), (ΩM = ΩT = 0.3), et (ΩM = 0.3, ΩΛ = 0.7).
On peut dire que la formation de structures cesse lorsque ΩM (a) tombe au dessous
d’environ ΩM = 0.5. Dans les trois cas, déterminer la valeur de a(t) ou cela se produit.
1.2 Pourquoi l’univers est-il en expansion ?
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
T
Y
L
PO
N
H
EC
E
U
IQ
E
L
2
CO
ÉChapitre
Cosmologie observationnelle
N
H
EC
E
U
IQ
Ce chapitre présente de façon plus détaillée les fondements observationnels de la
cosmologie standard. Nous allons d’abord passer en revue les objets astronomiques
que l’on trouve à diverses échelles. La section 1 est consacrée aux objets compacts
qui émettent les photons visibles de l’univers que ce soit par combustion nucléaire
(dans les étoiles) ou par eﬀondrement gravitationnel (dans l’eﬀondrement du cœur
des supernovae et dans les quasars). Les deux sections suivantes décrivent comment
les étoiles sont regroupées dans des galaxies et des amas de galaxies. Dans la section 4
nous ferons le bilan actuel des eﬀorts menés pour déterminer la nature de la matière
noire qui domine la massse de l’univers. Finalement, dans la section 5, nous résumerons
l’état actuel de la mesure des paramètres du modèle standard de le cosmologie, c’està-dire le taux d’expansion ainsi que les diverses densités universelles. La discussion
des observations des photons du fond cosmique CBR est reportée au chapitre 7.
ÉC
1
E
L
O
T
Y
L
PO
Étoiles et quasi-étoiles
Parmi les milliers d’objets astronomiques visibles à l’œil nu dans le ciel, presque
tous sont des étoiles proches (R < 50 pc). Les exceptions sont le Soleil, la lune, 5
planètes, 4 galaxies et, de temps à autre, des comètes. Les galaxies sont M31 (Andromède), le Grand et le Petit Nuage de Magellan (désignés respectivement par LMC et
SMC), et notre propre Voie Lactée. Même si la cosmologie observationnelle s’intéresse
d’abord aux échelles super-galactiques, il nous serait impossible de comprendre l’univers sans comprendre les étoiles. Dans cette courte section, nous ne pouvons donner
qu’une description assez superﬁcielle de l’astrophysique nécessaire pour la cosmologie.
Les étoiles commencent leur vie sous forme de nuages diﬀus composés principalement d’hydrogène et d’hélium. La première génération comporte le mélange primordial (75% d’hydrogène et 25% d’hélium en masse) produit par les réactions nucléaires dans l’univers primordial. Lorsque les nuages se contractent sous l’eﬀet de
leur propre poids, l’énergie de liaison (négative) se retrouve dans l’accroissement de
ÉC
E
L
O
Y
L
PO
57
H
C
TE
U
Q
I
N
E
58
E
U
IQ
Chapitre 2. Cosmologie observationnelle
T
Y
L
PO
N
H
EC
l’énergie thermique du nuage et dans l’énergie de corps noir rayonnée sous forme de
photons (exercice 2.10). La contraction cesse (temporairement) lorsque le cœur est
porté à une température suﬃsante pour que s’allument les réactions nucléaires 1 . À
ce stade, la puissance rayonnée est compensée par la puissance fournie par les réactions nucléaires et l’étoile peut subsister dans un état stationnaire tant qu’il reste du
combustible nucléaire.
La première série de réactions nucléaires transforme l’hydrogène en hélium. Les
étoiles qui sont dans cette phase de leur combustion constituent ce que l’on nomme
la « séquence principale ». La luminosité d’une étoile de la séquence principale est
grosso modo proportionnelle au cube de sa masse (exercice 2.10). Puisque la quantité
de combustible nucléaire est proportionnelle à la masse, la durée totale de la phase
de combustion de l’hydrogène est proportionnelle à M −2 . Le Tableau 1 donne les
caractéristiques de quelques étoiles de la séquence principale.
Après épuisement de l’hydrogène, l’hélium peut être brûlé pour donner des éléments plus lourds dans la phase « géante ». L’hélium brûlé donne d’abord du carbone
et de l’oxygène, et, dans les étoiles les plus massives, la combustion se poursuit jusqu’au 56 Fe, le troisième des noyaux les plus solidement liés.2
Une partie des éléments lourds produits dans les étoiles pourra ultérieurement être
dispersée dans l’espace interstellaire lors d’explosions de supernovae, terme de la vie
d’étoiles de masse supérieure à ∼ 2M . Il résulte de cette dispersion que dans les
générations ultérieures d’étoiles il entre en faible proportion des éléments plus lourds
que l’hélium (des « métaux » dans le jargon astronomique). Le Soleil, par exemple,
est né il y a 4.5 × 109 années avec ∼ 28% d’hélium (en masse) et ∼ 2% de métaux. On
voit que même les étoiles récentes ont une composition nucléaire peu éloignée de la
composition primordiale. La grande diversité des étoiles provient principalement des
diﬀérences de masse qui s’étalent de ∼ 0.1M à ∼ 50M (Tableau 1).
Dans les intérieurs stellaires, les photons ont une marche aléatoire jusqu’à ce qu’ils
atteignent un rayon où la densité est suﬃsamment faible pour qu’ils s’échappent. La
couche d’où les photons s’échappent s’appelle la « photosphère ». Si les photons
de toutes longueurs d’onde interagissaient avec la même section eﬃcace, le rayon
d’échappement serait indépendant de la longueur d’onde et les spectres stellaires seraient ceux de corps noirs presque parfaits, à la température de la photosphère. La
présence d’atomes non ionisés au voisinage de la photosphère provoque une dépendance de la section eﬃcace dans la longueur d’onde. Les photons de section eﬃcace
plus élevée s’échappent à des rayons plus grands, donc plus froids, ce qui entraîne que
les ﬂux sont plus faibles à ces longueurs d’ondes. Un exemple particulièrement simple
peut se voir sur le spectre d’une étoile A0 montrée sur la ﬁgure 2.1. Les étoiles de ce
type ont des températures de photosphère voisines de 16 000 Kelvin ce qui provoque
la présence abondante d’hydrogène dans les états n = 2. Les sections eﬃcaces des
ÉC
E
L
O
ÉC
E
L
O
T
Y
L
PO
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
1 Les réactions nucléaires ne se produisent qu’à haute température, T ∼ 1 keV, car elles sont
inhibées exponentiellement à basse température par la répulsion coulombienne entre noyaux, tous
chargés positivement.
2 Les noyaux les plus solidement liés sont 58 Fe et 62 Ni, mais ces deux noyaux ne peuvent pas être
produits dans les étoiles par des réactions à deux corps.
ÉC
E
L
O
E
Étoiles et quasi-étoiles
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
59
Tab. 2.1: Caractéristiques de quelques étoiles représentatives de la séquence principale [2].
Les étoiles sont classées selon leur type spectral (O, B, A, F, G, K, M) qui va du chaud au
froid. Chaque classe est divisée en sous-classes (0 à 9). Le tableau montre quatre exemples
allant de O5 (massives, brillantes, chaudes) à M5 (peu massive, peu lumineuses, froides).
Les deux premières lignes montrent la corrélation entre la masse et la luminosité. La durée
de vie τ sur la séquence principale correspond au temps nécessaire pour brûler l’hydrogène du
cœur stellaire (à peu près 10% de l’hydrogène total) à une luminosité grosso modo constante.
La température eﬀective de surface Ts et le rayon R sont reliés par la loi de Stefan. Les deux
lignes suivantes montrent comment la luminosité et la température de surface interviennent
dans la magnitude visuelle absolue MV et dans l’indice de couleur B − V . La dernière ligne
donne le nombre volumique local d’étoiles par unité de magnitude et montre que la plupart
des étoiles ont une masse relativement faible.
type
T
Y
L
PO
O5
A0
G2
60
2.9
LV /LV 8 × 105
τ /1010 an
N
H
EC
E
U
IQ
K5
M5
1.0
0.67
0.21
50
1.0
0.15
0.01
10−4
0.05
1
4
200
Ts (Kelvin)
44500
9520
5860
4350
3240
R/R
12.
2.4
1.0
0.72
0.27
MV
−5.7
0.6
4.7
7.4
12.3
B−V
−0.33
-0.02
0.65
1.15
1.64
dn/dMV (pc−3 )
10−8
10−4
3 × 10−3
3 × 10−3
10−2
E
L
O
M/M
ÉC
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
60
E
U
IQ
Chapitre 2. Cosmologie observationnelle
T
Y
L
PO
N
H
EC
photons sont par conséquent élevées aux longueurs d’ondes correspondant aux transitions (n = 2 → n ) et à celles de la photoionisation à partir de n = 2. Par conséquent,
le spectre contient les raies d’absoption de la série de Balmer ainsi que la « cassure
de Balmer » au voisinage du seuil d’ionisation λ = 370 nm.
Si l’on approxime la photosphère d’une étoile par un corps noir de température
déﬁnie, la luminosité de l’étoile est donnée par la loi de Stefan L = σTs4 πD2 où D
est le diamètre de la photosphère. La mesure du ﬂux φ = L/4πR2 donne alors une
estimation de la dimension angulaire de l’étoile :
ÉC
E
L
O
∆θ =
D
= 2
R
Å
φ
σTs4
ã1/2
,
(2.1)
où R est la distance de l’étoile. Par conséquent, la distance de l’étoile peut être évaluée
si l’on connaît sa taille angulaire, mais cela n’est facile que pour le Soleil.
Parmi les quantités données dans la Table 2.1, seules les grandeurs superﬁcielles
Ts et B − V sont directement mesurables à partir du ﬂux de photons observé. Les
autres grandeurs ne peuvent être déduites que si l’on connaît la distance de l’étoile. Par
conséquent, nous allons nous pencher sur le problème fondamental de la détermination
des distances stellaires.
À part la distance du Soleil, qui est mesurée de façon très précise au radar, les
distances stellaires sont extrêmement diﬃciles à mesurer. La distance d’étoiles de
diamètre connu peut être estimée par (2.1). Les diamètres peuvent être déterminés directement pour les étoiles binaires orientées de telle façon que les deux étoiles
s’éclipsent l’une l’autre périodiquement (exercice 2.9). Le diamètre d’une étoile dont
la photosphère est en expansion, comme une étoile pulsante ou une supernova, peut
être déterminée à partir de la vitesse de la photosphère que l’on détermine par la
position et la forme de ses raies spectrales (cf. chapitre 2, section 5.1).
En dehors de ces cas et de quelques autres exceptions assez rares, les distances
d’étoiles proches peuvent être déterminées par leur « parallaxe », c’est-à-dire leur
mouvement annuel apparent par rapport aux étoiles lointaines qui résulte du mouvement de la Terre autour du Soleil. Le principe de cette technique est illustré sur la
ﬁgure 2.2. L’excellente résolution angulaire du télescope monté sur le satellite Hipparcos [47] qui a fait des observations entre 1989 et 1993 a permis de mesurer la distance
de ∼ 105 étoiles à environ ∼ 200 pc avec une précision de l’ordre de 10%.
Pour les étoiles dont les distances R sont mesurées par parallaxe, la luminosité peut
être calculée par le ﬂux mesuré de photons φ = L/4πR2 , après quelques corrections
dues à l’absorption par la poussière interstellaire3. La luminosité calculée en fonction de la température de surface observée est montrée sur le diagramme « couleurmagnitude » des étoiles de Hipparcos sur la ﬁgure 2.3. La luminosité LV dans la plage
ÉC
E
L
O
T
Y
L
PO
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
3 La longueur d’absorption locale de la lumière dépend fortement de la ligne de visée. Dans le plan
galactique, elle est typiquement de l’ordre de 1 kpc pour des photons de λ ∼ 550 nm [48] Puisque
le taux d’absorption par la poussière est une fonction décroissante de la longueur d’onde, on peut
estimer cette absorption au travers du « rougissement » du spectre d’une étoile par rapport à celui
d’étoiles proches du même type.
ÉC
E
L
O
E
Étoiles et quasi-étoiles
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
T
Y
L
PO
E
U
IQ
N
H
EC
61
E
U
IQ
Fig. 2.1: Spectre d’une étoile « A0 » (λ en nm) [46]. Aux longueurs d’onde supérieures à
400 nm, le spectre suit de près celui d’un corps noir à T ∼ 16 000 Kelvin. À cette température,
une grande partie de l’hydrogène est dans l’état atomique n = 2 et les raies de la série de
Balmer de l’hydrogène (n = 2 → n ) sont clairement présentes. La forte absorption aux
longueurs d’onde plus courtes que la « cassure de Balmer » à ∼ 370 nm est due à la grande
section eﬃcace de photo-ionisation de l’hydrogène dans l’état n = 2 et à l’absorption par des
ensembles de raies proches les unes des autres. La température eﬀective de surface calculée
à partir de la luminosité totale est ∼ 9900 Kelvin.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
62
R
ÉC
D
E
U
IQ
Chapitre 2. Cosmologie observationnelle
E
L
O
T
Y
L
PO
N
H
EC
θ1
θ2
D
R= θ - θ
2
1
E
U
IQ
Fig. 2.2: Mesure de la distance R d’une étoile proche par la méthode du parallaxe. La distance
angulaire θ entre cette étoile et une étoile lointaine subit une modulation annuelle provenant
du mouvement de la Terre autour du Soleil. Dans le cas réaliste de petites modulations,
l’amplitude est θ2 − θ1 = D/R où D = 2 U A = 3 × 1011 m est le diamètre de l’orbite
terrestre. La modulation est de 1 arcsec pour une étoile à une distance de 1 parsec (ce qui
est la déﬁnition de cette unité de longueur).
E
L
O
T
Y
L
PO
N
H
EC
de longueurs d’onde « V » (λ ∼ 550 nm) est donnée en échelle logarithmique inverse
en fonction de la « magnitude absolue » MV :
ÉC
MV = −2.5 log LV + constante.
(2.2)
(La déﬁnition de la magnitude est expliquée dans l’appendice D.) L’échelle horizontale
donne « l’indice de couleur » B − V qui est la diﬀérence en magnitude entre la bande
« B » (λ ∼ 450 nm) et la bande V . Les étoiles de température de surface relativement
basse ont une valeur de B − V grande et celles de grande température de surface une
faible valeur de B − V .
La plupart des étoiles se trouvent sur la bande diagonale dans le diagramme
couleur-magnitude, là où la théorie de la structure stellaire place la séquence principale. Les étoiles les plus massives et brillantes ont les températures de surface les plus
élevées, les moins massives et moins lumineuses ont les températures de surface les
plus basses.
Certaines étoiles post-séquence principale sont sur l’extension diagonale du côté
froid de la séquence principale. Les étoiles géantes rouges du « clump »4 , au voisinage
de MV ∼ 0.75 et (B − V ) ∼ 1.0, qui brûlent leur hélium sont particulièrement
importantes.
La corrélation entre la luminosité et la couleur (Figure 2.3) engendre des corrélations entre le ﬂux et la couleur pour des étoiles groupées à une distance donnée. La
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
4 Ce terme désigne les étoiles qui, au sortir de la séquence principale forment , dans le diagramme
d’Herzprung-Russel une accumulation en touﬀe
ÉC
E
Étoiles et quasi-étoiles
-5
63
0
MV [mag]
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
5
10
ÉC
E
L
O
1
15
-0.5
T
Y
L
PO
N
H
EC
E
U
IQ
10
0.0
0.5
1.0
1.5
2.0
B - V [mag]
Fig. 2.3: Diagramme « couleur-magnitude » d’étoiles dont la distance a été mesurée par
parallaxe par le satellite Hipparcos [47] avec une précision de 10%. En ordonnée la magnitude
absolue dans la bande V (λ ∼ 550 nm) : MV = −2.5 log(LV ) + constant où LV est la
luminosité dans la bande V . (La déﬁnition de la magnitude est expliquée dans l’appendice
D.) En abscisse, l’indice de couleur (B − V ), c’est-à-dire la diﬀérence en magnitude entre
les bandes B (λ ∼ 450 nm) et V . L’indice de couleur est un indicateur de la température
de surface de l’étoile. Les étoiles brillantes et chaudes sont en haut à gauche, les étoiles peu
lumineuses et froides sont en bas à droite. La bande diagonale correspond à des étoiles sur la
séquence principale (qui brûlent de l’hydrogène). Les étoiles post-séquence principale sont sur
la diagonale perpendiculaire du côté froid de la séquence principale. Les étoiles accumulées
vers MV ∼ 0.75 et (B − V ) ∼ 1.0 sont des géantes rouges du clump brûlant de l’hélium. Un
petit nombre d’étoiles mortes (naines blanches) se trouvent vers MV ∼ 12, (B − V ) ∼ 0.
Figure de l’Agence Spatiale Européenne.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
64
ÉC
E
U
IQ
Chapitre 2. Cosmologie observationnelle
E
L
O
T
Y
L
PO
LMC−OUTER
N
H
EC
HODGE−10
HS275 (BAR)
16
16
18
18
E
U
IQ
20
22
24
ÉC
26
E
L
O
T
Y
L
PO
N
H
EC
22
F555W
F555W
20
24
26
28
28
0
.5
1
F555W−F814W
1.5
0
.5
1
1.5
F555W−F814W
Fig. 2.4: Diagramme couleur-magnitude (apparente) pour les étoiles de trois régions du
Grand Nuage de Magellan (LMC) mesuré par le télescope spatial Hubble [49]. En ordonnée
la magnitude apparente dans la bande F555W : F555W = −2.5 log(φ555W ) + constante où
φ555W est le ﬂux dans la bande 555W. (La longueur d’onde moyenne de F555W, 525 nm,
est proche de celle de la bande V usuelle de la ﬁgure 2.3). En abscisse, l’indice de couleur
(F555W−F814W), c’est-à-dire la diﬀérence en magnitude entre les bandes F555W et F814W
(λ ∼ 827 nm). L’indice de couleur est un indicateur de la température de surface de l’étoile.
En comparant les magnitudes apparentes des étoiles du LMC avec les magnitudes absolues
dans la Voie Lactée (Figure 2.3) on peut estimer la distance au LMC.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Étoiles et quasi-étoiles
T
Y
L
PO
N
H
EC
E
U
IQ
65
Figure 2.4 montre le diagramme couleur-magnitude d’étoiles du Grand Nuage de Magellan (LMC). Le ﬂux φV dans la bande de longueurs d’onde V est donné en échelle
logarithmique inverse en fonction de la « magnitude apparente », V :
ÉC
E
L
O
V = −2.5 log φV + constante.
(2.3)
En abscisse est porté un indice de couleur qui est un indicateur de la température de
surface. On est frappé par la similitude entre ce diagramme et le diagramme couleurmagnitude de Hipparcos sur la ﬁgure 2.3. Les étoiles de la séquence principale et
les géantes rouges du clump sont positionnées correctement, ce qui suggère que la
luminosité intrinsèque des étoiles du LMC est pratiquement la même que celle des
étoiles proches du système solaire. En faisant cette hypothèse, on peut estimer la
distance du LMC par la formule φV = LV /4πR2 . Dans le système des magnitudes, cela
est facile à faire car les constantes qui interviennent dans la déﬁnition des magnitudes
sont choisies de telle façon qu’en l’absence d’absorption la magnitude apparente est
égale à la magnitude absolue d’une étoile à une distance de 10 pc :
N
H
EC
V = MV + 5 log(R/10 pc) + A ,
T
Y
L
PO
E
U
IQ
(2.4)
où la constante A prend en compte l’absorption. En utilisant les magnitudes des
géantes rouges du clump dans la bande V et en négligeant l’absorption (faible dans
ce cas) on trouve
ÉC
E
L
O
RLMC ∼ 10 pc × 100.2(19.25−0.75) ∼ 50 kpc .
(2.5)
Ce résultat est correct à 10% près.
Les techniques traditionnelles d’« étalonnage des distances » 5 pour la mesure des
distances galactiques sont des variantes du calcul ci-dessus de la distance du LMC.
L’étalonnage consiste à déﬁnir des plages de distances à l’intérieur desquelles plusieurs
méthodes de détermination des distances peuvent être utilisées. Le raccordement de
deux plages contiguës passe par des « barreaux » d’échelle qui constituent souvent
le point faible du dispositif. Elles utilisent toutes divers types d’objets de luminosité
connue appelés collectivement des « chandelles standard ». La technique n’est sûre
que si l’on peut négliger ou estimer l’absorption et si les diﬀérences intrinsèques de
luminosité entre chandelles lointaines et chandelles proches peuvent être estimées.
Dans l’exemple ci-dessus, on sait que la composition chimique des étoiles du LMC
est légèrement diﬀérente de celle des étoiles du voisinage du Soleil. Cela peut rendre,
par exemple, la luminosité des géantes rouges du clump diﬀérente dans le LMC et
au voisinage du Soleil, et par conséquent modiﬁer les estimations de distances si l’on
n’en tient pas compte [50]. Notons que l’utilisation de chandelles standard diﬀérentes
donne des distances du LMC qui diﬀèrent d’environ 10% [51, 21].
Y
L
PO
H
C
TE
U
Q
I
N
5 Les subtilités respectives de l’anglais et du français nous mènent une fois de plus à déﬁnir un
mot inhabituel dans le jargon astronomique. De fait aux deux mots anglais « scale » et « ladder »
n’en correspond qu’un seul en français : échelle. Dans ce texte, le mot d’échelle apparaît si souvent
que l’on se perd facilement dans le sens de ce que l’on peut lire sans la précaution élémentaire d’en
introduire un autre.
ÉC
E
L
O
E
66
E
U
IQ
Chapitre 2. Cosmologie observationnelle
T
Y
L
PO
N
H
EC
On ne peut utiliser les étoiles de la séquence principale ou les géantes rouges du
clump comme indicateurs de distances que si elle sont à des distances < 1 Mpc. Audelà, ces étoiles sont d’un éclat trop faible pour être résolues. À des distances allant
jusqu’à ∼ 50 Mpc on peut utiliser les étoiles variables appelées Céphéides comme
indicateurs de distances. Les Céphéides sont une classe d’étoiles post-séquence principale qui ont des luminosités périodiques dans le temps. Leur magnitude absolue
est MV ∼ −4 c’est-à-dire qu’elles sont 100 fois plus brillantes que les géantes rouges
du clump et peuvent donc être identiﬁées à des distances supérieures. La luminosité
d’une Céphéide est une fonction connue de sa période comme on peut le voir sur la
ﬁgure 2.5 pour les Céphéides du LMC. La magnitude absolue des Céphéides peut être
déterminée à partir du petit nombre de celles pour qui l’on possède des mesures de
parallaxe par Hipparcos [52]. Toutefois, comme ces dernières sont peu nombreuses, la
plupart des auteurs préfèrent utiliser les Céphéides du LMC aﬁn de calibrer la relation période-luminosité. Cette méthode demande bien entendu que l’on utilise, pour
déterminer la distance du LMC, d’autres objets, comme les géantes rouges du clump
ou des binaires à éclipses (exercice 2.9).
Les « étoiles » les plus brillantes sont les explosions de supernovae (Fig. 2.6). On
pense que celles-ci sont de deux types. Le premier type consiste en des supernovae à
« eﬀondrement du cœur ». Le progéniteur d’un tel objet est une étoile très massive
où le cœur a brûlé jusqu’au 56 Fe.
Lorsque le cœur atteint la masse de Chandrasekhar6 (∼ 1.4M ), le cœur s’eﬀondre
et devient une étoile à neutrons. On pense que ce mécanisme est à l’origine des supernovae de classiﬁcation spectrale de type II et de type Ic. L’énergie gravitationnelle
négative de l’étoile à neutron est compensée par l’émission de neutrinos. Les neutrinos sont rayonnés de préférence aux photons car leur grand libre parcours moyen leur
facilite considérablement la sortie au travers de la matière stellaire environnante par
rapport aux photons. Puisque la masse de l’étoile à neutrons est toujours voisine de
la masse de Chandrasekhar, ces supernovae sont des « chandelles standard à neutrinos ». Cette hypothèse a été conﬁrmée par la détection des neutrinios émis par la
supernova SN1987a dans le LMC.
Le deuxième type de supernova, plus brillant, le type Ia, est le plus utile pour
la cosmologie. Ces supernovae sont, on le pense, des explosions thermonucléaires de
naines blanches de carbone et d’oxygène dont la masse se trouve portée au delà de
la masse de Chandrasekhar par accrétion de matière provenant de leur étoile partenaire dans un système binaire. Lorsque la limite est atteinte, l’étoile commence par
imploser et l’augmentation résultante de densité et de température provoque la combustion explosive du mélange carbone/oxygène en 56 Ni. La majeure partie de l’énergie
de réaction se retrouve sous forme d’énergie cinétique du 56 Ni éjecté. La luminosité
provient principalement de la désintégration radioactive du 56 Ni en 56 Co puis en 56 Fe.
Puisque la masse totale de 56 Ni est toujours voisine de la masse de Chandrasekhar,
les supernovae de type Ia sont pratiquement des « chandelles standard à photons »
ÉC
E
L
O
ÉC
E
L
O
T
Y
L
PO
E
L
O
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
6 La masse de Chandrasekhar ∼ m 3 /m 2 est la masse maximum qu’un objet peut avoir pour
p
pl
que la pression des électrons dégénérés puisse empêcher l’eﬀondrement gravitationnel.
ÉC
E
Étoiles et quasi-étoiles
<V0>
<V0>
ÉC
E
L
O
T
Y
L
PO
N
H
EC
13
14
15
16
17
E
U
IQ
67
E
U
IQ
LMC Cepheids
13
14
15
16
17
ÉC
E
L
O
-.5
T
Y
L
PO
0
N
H
EC
.5
FU
1
1.5
log P
Fig. 2.5: Magnitude apparente V en fonction de la période P en jours pour un lot de Céphéides dans le LMC, mesurée par la collaboration OGLE [53]. Le tableau supérieur montre
deux types de Céphéides, les Céphéides « fondamentales » qui pulsent à la fréquence fondamentale et les « Céphéides de première harmonique » qui ont une période deux fois plus
petite que les fondamentales. Le tableau du bas ne montre que les Céphéides fondamentales
où le meilleur ajustement est V = −2.765 log P + 17.044. La magnitude apparente des Céphéides peut être utilisée pour déterminer la distance au LMC en utilisant la magnitude
absolue des Céphéides de Hipparcos. Réciproquement, la magnitude apparente peut être utilisée pour déterminer la magnitude absolue en utilisant les mesures de distance du LMC faites
par d’autres méthodes.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
68
E
U
IQ
Chapitre 2. Cosmologie observationnelle
T
Y
L
PO
N
H
EC
Supernova 1998ba
Supernova Cosmology Project
(Perlmutter, et al., 1998)
ÉC
E
L
O
(as seen from
Hubble Space
Telescope)
3 Weeks
Before
Supernova
Discovery
(as seen from
telescopes
on Earth)
N
H
EC
E
U
IQ
Difference
ÉC
E
L
O
T
Y
L
PO
Fig. 2.6: Découverte d’une supernova à z = 0.43 par le Supernova Cosmology Project [26].
La ﬁgure montre une portion de 0.06 deg2 d’une image CCD du ciel prise avec des télescopes
basés sur Terre. La plupart des objets sont des galaxies lointaines. Les panneaux marqués « 3
weeks before » et « supernova discovery » montrent des zooms de la grande image prises à
des intervalles de trois semaines. Le panneau « supernova discovery » montre qu’une des
galaxies a une augmentation de luminosité apparente et un léger changement de forme dus
à l’explosion d’une supernova entre les deux prises de vue. Dans le panneau « diﬀerence »,
l’image ne montre que la supernova, le fond ayant été soustrait numériquement. Le dernier
panneau montre la même région du ciel vu par le Hubble Space Telescope. Comme elle ne
souﬀre pas du ﬂou provoqué par l’atmosphère, l’image HST montre que l’explosion de la
supernova a eu lieu sur les bord de la galaxie qui l’héberge. Avec la permission de Saul
Perlmutter.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Étoiles et quasi-étoiles
T
Y
L
PO
N
H
EC
E
U
IQ
69
ce qui les rend extrêmement utiles pour la détermination des distances. Elles sont
suﬃsamment brillantes pour être vues à des redshifts voisins de un. Le seul problème
est qu’elles sont rares, environ une explosion par galaxie et par siècle, qui reste visible
pendant environ un mois. La « courbe de lumière » (ﬂux en fonction du temps) d’une
supernova de type 1a est représentée sur la ﬁgure 2.7.
La luminosité au maximum de la courbe de sept supernovae de type Ia qui se
sont produites dans des galaxies ou amas de galaxies qui ont des distances mesurables
par Céphéides a pu être mesurée. Les sept magitudes absolues sont représentées sur
la ﬁgure 2.8. On peut voir une légère corrélation entre la luminosité maximale et la
durée de l’explosion paramétrisée par la variable ∆m15 , c’est-à-dire le changement
en magnitude 15 jours après la passage par la luminosité maximum. On voit que les
supernovae les plus brillantes sont celles de plus longue durée (petit ∆m15 ). Bien que
ceci ne soit pas complètement compris, on pense que cette corrélation est un reﬂet de
l’abondance relative de carbone et d’oxygène dans l’étoile progénitrice.
Les objets les plus lumineux sont les « quasars » ou « QSO » (objets quasistellaires) [55]. Leur luminosité atteint 100 fois celle d’une galaxie brillante. On pense
que les quasars consistent en un trou noir massif M ∼ 108 M entouré de nuages
gazeux. Si cette idée est vraie, la source de leur énergie serait l’accrétion du gaz
environnant par le trou noir, l’augmentation d’énergie de liaison gravitationnelle s’accompagnant d’une émission de photons. Le spectre d’un quasar typique est présenté
sur la ﬁgure 6.7. Ce n’est pas un spectre thermique ; il possède un pic proéminent
du à l’émission « Lyman-α » par l’hydrogène atomique (n = 2 → n = 1) du gaz
environnant. Comme ils sont très brillants, les quasars peuvent être observés à de très
grands redshifts, le plus grand à ce jour étant z ∼ 5.
Il y a deux raisons pour lesquelles les quasars sont importants en cosmologie.
Tout d’abord, comme ce sont les objets les plus anciens que l’on ait identiﬁés, ils
fournissent de précieuses indications pour la théorie de la formation des structures.
Cette dernière doit notamment se produire suﬃsamment rapidement pour fabriquer
des objets à z ∼ 5. La grande masse des quasars suggère également que ceux-ci ont
joué un rôle important dans la formation des premières galaxies. (Les galaxies les plus
anciennes que l’on ait identiﬁées ont, elles aussi, des redshifts ∼ 5.)
Deuxièmement, les spectres des quasars montrent des raies d’absorption provenant
des éléments présents dans les nuages interstellaires sur la ligne de visée. Ils constituent
par conséquent un important moyen pour sonder le milieu intergalactique. Le spectre
de la ﬁgure 6.7 montre ainsi une « forêt » d’absorption de raies « Lyman-α » sur
le versant bleu des raies d’absorption de l’émission Lyman-α du quasar lui-même.
Lorsque les photons voyagent du quasar vers nous, leur énergie est dégradée par le
redshift cosmologique. Quand il traverse un nuage de redshift znuage , un photon sera
résonant à Lyman-α si l’énergie des photons initiaux E1 satisfait (zquasar +1)/(znuage +
1) = E1 /ELy−α , où ELy−α est l’énergie de la transition Lyman-α. La forêt de raies
d’absorption correspond ainsi à une série de nuages entre le quasar et nous, chaque
nuage absorbant seulement les photons dont les énergies ont été dégradées d’une
quantité bien précise. Le nombre volumique de ces nuages impose des contraintes
importantes sur la théorie de la formation des structures et permet de déterminer la
ÉC
E
L
O
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
E
70
ÉC
E
U
IQ
Chapitre 2. Cosmologie observationnelle
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
T
Y
L
PO
N
H
EC
E
U
IQ
U
Q
I
N
Fig. 2.7: Courbe de lumière (magnitude en fonction du temps) pour une supernova typique de
type Ia [54]. La comparaison de la magnitude apparente du pic avec les magnitudes absolues
de la ﬁgure 2.8 détermine la distance de la supernova.
ÉC
E
L
O
Y
L
PO
H
C
TE
E
Étoiles et quasi-étoiles
ÉC
E
L
O
−20
T
Y
L
PO
N
H
EC
E
U
IQ
71
B
−19
Cepheid (host)
Cepheid (group/cluster)
Distant SNe Ia (Ho=65)
−18
−20
Mmax
V
−19
−18
ÉC
−20
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
I
−19
−18
0.8
1
1.2
∆m15(B)
1.4
1.6
1.8
U
Q
I
N
Fig. 2.8: Magnitude absolue au maximum de luminosité dans les bandes B, V et I de
H
C
TE
supernovae de distance connue [54]. Les sept supernovae spéciﬁées ont explosé dans des
galaxies dont les distances ont pu être mesurées par des Céphéides. La distance des autres
supernovae a été calculée à partir de leur redshift en posant H0 = 65 km s−1 Mpc−1 . La
magnitude absolue au pic montre une légère dépendance en ∆m15 , c’est-à-dire la diﬀérence
de la magnitude au maximum de luminosité et de celle observée 15 jours plus tard.
ÉC
E
L
O
Y
L
PO
E
72
E
U
IQ
Chapitre 2. Cosmologie observationnelle
T
Y
L
PO
N
H
EC
Tab. 2.2: Sources de masse et de luminosité dans le voisinage du Soleil, à 8 kpc du centre
galactique [3, 21]. On pense que la matière noire a deux composantes. La première est conﬁnée
dans le disque galactique et a une densité que l’on évalue à partir du mouvement des étoiles
perpendiculairement au plan galactique. On pense que la seconde composante, le « halo »,
est de forme à peu près sphérique. Sa masse totale se déduit de la courbe de rotation de la
galaxie
ÉC
E
L
O
composante
densité de masse
(M pc−3 )
densité de luminosité
(L pc−3 )
étoiles visibles
0.044
0.067
étoiles mortes
0.028
0
gaz
0.042
matière noire
(disque)
< 0.07
E
L
O
matière noire
(halo)
ÉC
N
H
EC
0
T
Y
L
PO
0.003 − 0.017
(0.1 − 0.7 GeV cm−3 )
E
U
IQ
0
0
quantité et l’état chimique de l’hydrogène local. Nous verrons notamment au chapitre
5 que le fait que les photons super-Lyman-α nous parviennent indique que la plus
grosse partie de l’hydrogène qui se trouve entre nous et les quasars à grand redshift
est ionisé.
2
Galaxies
U
Q
I
N
Les galaxies sont des amas d’étoiles, de gaz et de matière noire. Les plus grandes
comportent de l’ordre de 1011 étoiles. Elles présentent toute une diversité de morphologies, que l’on classe grosso modo en « elliptiques », « spirales » et « irrégulières ».
La Voie Lactée est une galaxie spirale et les caractéristiques du voisinage du Soleil
(Table 2.2) donnent une indication de l’environnement d’un disque galactique typique à 8 kpc du centre galactique. Notons la valeur du rapport masse-luminosité,
M/L ∼ 2.5M/L , qui, à un facteur deux près, est typique de la partie visible de
toutes les galaxies.
Comme pour une étoile, les seuls paramètres observables d’une galaxie sont sa
position dans le ciel, son ﬂux de photons, et la forme de son spectre (Figure 2.9). En
ÉC
E
L
O
Y
L
PO
H
C
TE
E
Galaxies
T
Y
L
PO
N
H
EC
E
U
IQ
73
utilisant les redshifts et la loi de Hubble pour déterminer les distances galactiques, on
s’aperçoit que les galaxies ont la distribution en luminosité très étalée, montrée sur la
ﬁgure 2.10. La partie brillante de la distribution décroît à peu près exponentiellement
avec une luminosité moyenne de
ÉC
E
L
O
10
L∗ ∼ 2.0 h−2
70 × 10 L .
(2.6)
Le facteur h−2
70 vient de l’utilisation de la loi de Hubble dans la détermination des
distances galactiques, R = H0−1 z. Il y a une divergence logarithmique apparente
dans la distribution de luminosité aux faibles luminosités, ce qui fait que le nombre
total de galaxies est mal déﬁni. Les galaxies de faible luminosité contribuent peu
à la luminosité totale de l’univers et, en supposant des rapports masse-luminosités
raisonnables, contribuent peu à sa masse totale.
Outre l’utilisation de la loi de Hubble, les distances galactiques peuvent être déterminées en mesurant le ﬂux lumineux d’objets de luminosité connue. Les objets les
plus sûrs sont les Céphéides (pour des distances R < 50 Mpc) et les supernovae de
type Ia (pour z ≤ 1.5). L’utilisation des Céphéides a permis de calibrer les relations
empiriques entre les luminosités galactiques et les caractéristiques observables. S’agissant des galaxies spirales, une formule très utile est la loi de « Tully–Fisher » qui relie
les luminosités galactiques à leur dispersion en vitesse (ﬁgure 2.11). La dispersion des
vitesses dans une galaxies est un indicateur de sa masse, par conséquent la relation de
Tully–Fisher est liée au rapport masse-luminosité. Une fois calibrée avec les galaxies
à Céphéide, la relation de Tully–Fisher permet de convertir les ﬂux galactiques en
distances jusqu’à R ∼ 200 Mpc.
La masse des galaxies peut être estimée à partir des vitesses d’étoiles ou de
nuages gazeux en orbite dans ces galaxies (exercice 2.8). D’après la dynamique newtonienne, la vitesse circulaire v(r) à la distance r du centre galactique est donnée
par v(r)2 ∼ GM (r)/r où M (r) est la masse à l’intérieur du rayon r. La ﬁgure 2.12
montre la courbe de rotation v(r) d’une galaxie spirale. La vitesse est celle de nuages
d’hydrogène atomique mesurée par le déplacement Doppler de la raie hyperﬁne de
21 cm de l’état fondamental de l’hydrogène. La courbe de rotation est plate à des
distances supérieures au rayon visible de la galaxie, ce qui indique une dépendance
M (r) ∝ r. Puisque la courbe de rotation reste plate jusqu’au dernier point mesuré,
r ∼ 30 h−1
70 kpc, on ne peut déduire qu’un limite inférieure sur la masse galactique ou
sur le rapport masse-luminosité :
ÉC
E
L
O
T
Y
L
PO
N
H
EC
M/L > 20 h70 M /L .
E
U
IQ
H
C
TE
U
Q
I
N
(2.7)
Le facteur h70 provient de l’utilisation de la loi de Hubble pour convertir les écarts
angulaires ∆θ en distances physiques r = R/∆θ = H0−1 z/∆θ. La limite inférieure
sur M/L est de 5 à 10 fois supérieure au rapport masse-luminosité du voisinage du
Soleil. La valeur élevée de M/L indique (par déﬁnition) la présence de matière noire
qui domine les masses galactique.
Le nombre volumique de galaxies brillantes, moyenné sur des volumes de ∼ (100 Mpc)3
ÉC
E
L
O
Y
L
PO
E
74
E
U
IQ
Chapitre 2. Cosmologie observationnelle
T
Y
L
PO
N
H
EC
(a) 9410 f105#14: cz = 35277 km/s, error = 44 km/s
E
L
O
150
ÉC
100
Hβ
50
G band
Mg I
0
CN Ca H
counts
Ca K
3500
4000
4500
5000
T
Y
L
PO
N
H
EC
5500
6000
E
U
IQ
6500
(b) 9410 f139#22: cz = 22535 km/s, error = 31 km/s
E
L
O
200
ÉC
[OIII] 4959
[OII] 3727
150
[OIII] 5007
100
Hβ
50
0
3500
4000
4500
5000
5500
6000
6500
wavelength (Angstroms)
Y
L
PO
H
C
TE
U
Q
I
N
Fig. 2.9: Spectre de deux galaxies obtenus dans l’observation du redshift par LCRS [56].
Comme le spectre d’une galaxie est la somme des spectres des étoiles qu’elle contient, il
montre les mêmes raies spectrales que ceux montrés sur la ﬁgure 2.1. Les raies d’émission
galactiques proviennent de gaz interstellaire chaud excité par les photons ultraviolets d’étoiles
massives ou de quasars dans la galaxie.
ÉC
E
L
O
E
Galaxies
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
75
.1
-3
luminosity function φ (Mpc )
.01
.001
T
Y
L
PO
N
H
EC
E
U
IQ
North+South 112 -23.0 < M < -17.5
.0001
ÉC
10
-5
10
-6
E
L
O
-23
-22
-21
-20
-19
absolute magnitude M
-18
-17
-16
Fig. 2.10: Spectre de magnitude absolue de galaxies obtenu dans l’observation du redshift par
LCRS [57]. Les magnitudes absolues ont été calculées en supposant H0 = 100 km s−1 Mpc−1 .
On notera la divergence logarithmique aux faibles luminosités et la coupure exponentielle au
10
L
delà de L∗ ∼ 2.0 h−2
70 × 10
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
76
ÉC
E
U
IQ
Chapitre 2. Cosmologie observationnelle
E
L
O
T
Y
L
PO
N
H
EC
T
Y
L
PO
N
H
EC
E
U
IQ
Fig. 2.11: Magnitude absolue dans la bande I de galaxies spirales dont les distances sont
mesurées par des Céphéides [30]. La magnitude est linéaire en log ∆v où ∆v est la dispersion
en vitesse mesurée en km s−1 .
est
ÉC
E
L
O
ngal ∼ 0.005 h370 Mpc−3 .
(2.8)
et la luminosité totale (dans la bande V ) est [3]
J0 = (1.2 ± 0.4) h70 × 108 L Mpc−3
(∼ ngal L∗ ).
(2.9)
Une limite inférieure sur la densité moyenne universelle associée aux galaxies se calcule
de la meilleur façon en utilisant J0 et la limite inférieure (2.7) sur M/L :
ρgal = J0 M/L > 2.4 h270 × 109 M Mpc−3 .
(2.10)
U
Q
I
N
On obtient ainsi une limite inférieure à la contribution des galaxies à ΩT
Ωgal > 0.02 .
3
Amas de galaxies
Y
L
PO
H
C
TE
(2.11)
Les galaxies sont souvent liées gravitationnellement en amas. Notre propre galaxie
appartient au « groupe local » qui comporte une douzaine de petites galaxies en
plus des deux grandes galaxies spirales que sont la Voie Lactée et Andromède (M31).
Les structures liées les plus grandes que l’on connaisse sont des « amas riches » de
ÉC
E
L
O
E
Amas de galaxies
18
µ r (mag arsec −2 )
ÉC
E
L
O
T
Y
L
PO
20
N
H
EC
E
U
IQ
77
NGC 3198
22
24
26
Vc (km s−1)
200
E
L
É C100O
T
Y
L
PO
N
H
EC
E
U
IQ
stars + gas
gas
10
20
30
40
Radius (kpc)
U
Q
I
N
Fig. 2.12: Courbe de rotation de la galaxie NGC3198 [58]. Le panneau du haut montre la
H
C
TE
distribution de luminosité qui indique que la majorité de la matière lumineuse est concentrée
sur des distances inférieures à 5 kpc du centre. Le panneau inférieur montre la courbe de
rotation mesurée. La courbe reste plate bien au delà du rayon auquel se trouve la matière
lumineuse, ce qui indique que de la matière noire est présente loin du centre. La courbe
« stars and gas » donne la courbe de rotation que l’on devrait observer si la distribution de
masse suivait la distribution de luminosité avec un rapport masse-luminosité de 3.8M /L .
L’échelle horizontale est prise pour H0 = 75 km s−1 Mpc−1 .
ÉC
E
L
O
Y
L
PO
E
78
E
U
IQ
Chapitre 2. Cosmologie observationnelle
N
H
EC
galaxies qui peuvent contenir des milliers de galaxies et jusqu’à 1015 h−1
70 M dans des
volumes de quelques Mpc3 . Cette masse correspond à une distribution uniforme qui
serait contenue dans une sphère de rayon ∼ 10 h−1
70 Mpc, si bien que les amas riches
ont des sur-densités de l’ordre de 1000. L’amas riche le plus proche de nous est l’Amas
de la Vierge qui est à une distance de ∼ 20 Mpc.
Les amas comme celui de la ﬁgure 2.13 sont assez mal déﬁnis si on les regarde
comme de simples collections de galaxies. Ils sont nettement mieux déﬁnis si on les
observe au travers de leur émission de rayons X. Les rayons X sont produits par
bremsstrahlung d’électrons dans le gaz intergalactique ionisé. On pense que ce gaz
constitue la plus grande partie de la masse baryonique des amas.
La masse des amas peut être assez facilement estimée en mesurant la dispersion
en vitesse des galaxies de l’amas et en appliquant le théorème du viriel (exercice 2.7).
Des techniques plus modernes utilisent la température en rayons X (exercice 2.11)
ou la forme de galaxies lontaines dont l’image est déformée par l’eﬀet de lentille
gravitationnelle de l’amas (voir chapitre 3, section 8). Les amas les plus massifs ont
un rapport masse-luminosité de l’ordre de 200 [59] :
ÉC
E
L
O
T
Y
L
PO
LY T
N
H
EC
E
U
IQ
M
M
.
∼ 200 h70
L
L
O
P
E
L
ÉCO
(2.12)
La masse du gaz de l’amas peut être estimée à partir du ﬂux observé de rayons X
(exercice 2.11). L’observation montre qu’elle est inférieure d’un ordre de grandeur à
la masse totale [60] :
Mgaz
Mbaryons
−3/2
∼
∼ 0.12 h70 .
Mtotale
Mtotale
(2.13)
Ce facteur 10 est probablement la meilleure indication observationnelle de l’existence
d’une matière noire non-baryonique car il serait diﬃcile de cacher 90% des baryons
d’un amas. Comme dans les halos galactiques, l’endroit le plus plausible pour cacher
des baryons serait dans des objets compacts sombres ou dans des nuages de gaz
moléculaire froid.
À des échelles supérieures à celles des amas de galaxies, les relevés de galaxies
à grand redshift montrent que les galaxies apparaissent comme groupées selon des
« parois » ﬁlamenteuses, entourant parfois de larges espaces vides qui contiennent
peu de galaxies visibles. La ﬁgure 2.14 montre une « tranche » du ciel vue dans le
relevé de redshift de Las Campanas. Les parois, ou les vides, les plus grands ont des
tailles de l’ordre de 10 000 km s−1 dans l’espace des vitesses ou de 140 h−1
70 Mpc dans
l’espace habituel. Ces structures ne sont pas liées et participent toujours à l’expansion
universelle, toutefois à un taux réduit à cause de leur auto-gravitation. Comme nous
le discutons dans la section 2.6 du chapitre 1, la question de savoir si ces ﬂuctuations
de densité formeront ou non un jour des structures liées dépend du fait que ΩM soit
ou non toujours suﬃsamment proche de 1.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Amas de galaxies
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
T
Y
L
PO
E
U
IQ
N
H
EC
79
E
U
IQ
U
Q
I
N
Fig. 2.13: L’amas de galaxies RXJ1347.5-1145 [61]. Les contours indiquent le niveau d’émis-
H
C
TE
sion de rayons X par le gaz ionisé intergalactique dans l’amas. L’amas forme une lentille
gravitationnelle pour les galaxies situées derrière lui. Les images de galaxies lointaines sont
en forme d’arcs notés A, B, C, D, et E. Avec la permission de S. Schindler.
ÉC
E
L
O
Y
L
PO
E
80
T
Y
L
PO
N
H
EC
13
ÉC
E
U
IQ
Chapitre 2. Cosmologie observationnelle
14
E
L
O
15
h
12
h
h
11
RA
h
h
10
h
o
-3 o
-6 o
-12
60
50
Dec
40
30
North
11263 galaxies
O
P
E
L
ÉCO
South
LY T
N
H
EC
E
U
IQ
cz (1000 km/s)
20
10
10
20
12434 galaxies
30
40
50
60
21
o
-45 o
-42 o
-39
h
22
h
23
h
0
ÉC
h
PO
E
OL
T
Y
L
1
h
2
H
C
E
h
3
h
U
Q
I
N
4
h
Fig. 2.14: Distribution spatiale de galaxies dans des « tranches » du ciel observée par le
Las Campanas Redshift Survey [56]. Notre galaxie est située à l’intersection des tranches
nord et sud. Les autres galaxies sont dans 6 tranches du ciel chacune de 110 degrés (dans le
plan de la ﬁgure) par 1.5 degré (perpendiculairement à la ﬁgure). Les distances radiales sont
mesurées en vitesse de récession v = cz où z est le redshift. Les distances spatiales peuvent
être estimées à partir de la loi de Hubble : R = cz/H0 ⇒ 10 000 km s−1 = 140 h−1
70 Mpc. On
observe des « murs » et des « vides » de taille allant jusqu’à ∼ 150 h−1
70 Mpc.
E
La matière noire
4
La matière noire
T
Y
L
PO
N
H
EC
E
U
IQ
81
Il y aura incontestablement des doutes sur le modèle cosmologique standard tant
que l’on n’aura pas identiﬁé ce qu’est la matière noire. Nous allons ici passer en revue
les tentatives eﬀectuées pour détecter les deux candidats non-baryoniques les plus en
vogue, les wimps et les axions. Nous décrirons aussi les investigations concernant des
objets sombres astrophysiques dans le halo galactique visibles au travers de l’eﬀet de
lentille gravitationnelle.
ÉC
4.1
E
L
O
Les wimps
Depuis les années 80, les wimps (weakly interacting massive particles) ont toujours constitué les candidats standard pour la matière noire froide (CDM). La raison
première pour introduire de telles particules provient de la formation des structures
(Chap. 7) qui suggère l’existence de CDM. Les extensions supersymétriques du modèle standard des particules élémentaires (qui ont été inventées pour résoudre des
problèmes qui n’ont rien à voir avec la matière noire) prévoient l’existence de telles
particules. Qu’elles n’aient pas encore été détectées dans les accélérateurs laisse à
penser qu’elles ont une masse mχ > 30 GeV [62]. Ces particules auraient été produites thermiquement dans l’univers primordial (Chapitre 6) ce qui donnerait une
abondance cosmologique inversement proportionnelle à leur section eﬃcace d’annihilation. Les modèles supersymétriques comportent de nombreux paramètres libres
ce qui mène à des densités actuelles dans un (vaste) domaine de quelques ordres de
grandeur de part et d’autre de la densité critique.
On s’attendrait à ce qu’aujourd’hui les wimps peuplent les halos de galaxies spirales
comme la nôtre. À partir de la vitesse de rotation galactique, on peut estimer que la
densité locale est de l’ordre de 0.3 GeV cm−3 [37]. La vitesse orbitale d’objets piégés
dans la galaxie est de l’ordre de 250 km s−1 , par conséquent, le ﬂux local de wimps
est de l’ordre de 107 × (1 GeV/mχ ) cm−2 s−1 .
Goodman et Witten [63] ont proposé que ces wimps pourraient être détectés en
observant le recul de noyaux dans des collisions élastiques wimps-noyaux. Des wimps
galactiques de masse dans le domaine du GeV ont des énergies cinétiques de l’ordre
keV et l’on s’attend donc à des reculs de l’ordre du keV. Le taux est proportionnel
à la section eﬃcace élastique de collision wimp-noyau qui dépend des paramètres des
modèles de physique des particules. Des valeurs typiques de ces sections eﬃcaces sont
de l’ordre de 10−44 cm2 , ce qui correspond à une interaction extrêmement faible.
Des diﬀusions de wimps peuvent être observées avec des techniques dites « calorimétriques » (Figure 2.15). Malheureusement, il est diﬃcile de distinguer les événements de wimps des événements provenant de la radioactivité bêta ou gamma (montrées sur cette ﬁgure). Statistiquement, un signal de wimps peut être isolé au travers
de la modulation saisonière attendue de ∼ 5% du taux d’événements [37, 64]. Cette
modulation provient de ce que lorsque le système solaire évolue dans le gaz (isotrope)
de wimps, le mouvement de la terre autour du Soleil s’ajoute ou se retranche dans la
vitesse du détecteur de wimps. Une alternative est que certains détecteurs peuvent
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
E
82
E
U
IQ
Chapitre 2. Cosmologie observationnelle
T
Y
L
PO
N
H
EC
faire la distinction entre les reculs nucléaires et le fond dû à la diﬀusion Compton
d’électrons [65, 66]. C’est le cas des détecteurs hybrides cryogéniques qui peuvent
détecter deux types d’excitations, les phonons et l’ionisation, ou les phonons et la
scintillation. Le rapport des deux signaux est diﬀérent s’agissant de reculs nucléaires
et d’électrons Compton, ce qui permet d’éliminer le bruit de fond.
La génération actuelle d’expériences utilisant soit des scintillateurs à NaI [67],
soit des diodes à germanium [68], soit des calorimètres cryogéniques hybrides germanium/silicium [65, 66] ont des bruits de fond qui les rend insensibles à la plupart des
types de matière noire supersymétrique. Les modèles supersymétriques qui ont les
sections eﬃcaces élastiques les plus élevées donnent des taux un peu au dessous du
niveau de bruit actuel, mais la plupart donnent des taux inférieurs d’au moins deux
ordres de grandeur aux limites actuelles.
En dépit du manque d’enthousiasme des théoriciens, une expérience [67] utilisant
des scintillateurs à NaI a annoncé un taux de comptage qui présente une modulation
annuelle que l’on attendrait de la part de wimps de masse
ÉC
E
L
O
mχ ∼ 50 ± 10 GeV .
C
E
T
LY
La section eﬃcace wimp-nucléon que l’on en déduit est
HN
E
U
IQ
σ ∼ 6 ± 2 × 10−42 cm2 .
O
P
E
L
ÉCO
(2.14)
(2.15)
Ce signal n’a pas été conﬁrmé jusqu’à présent par une expérience concurrente [65]
utilisant des détecteurs calorimètriques cryogéniques hybrides germanium/silicium.
Cette expérience donne pour une limite supérieure
σ < 2.5 × 10−42 cm2 .
(2.16)
La sensibilité des expériences s’améliore rapidement, et ce conﬂit devrait bientôt être
réglé.
À côté de la détection directe, il est possible de détecter le wimps indirectement
au travers de la détection de particules produites dans l’annihilation wimp-antiwimp
aujourd’hui. L’annihilation des wimps a cessé dans l’univers primordial à cause de
l’expansion universelle, mais elle a recommencé lorsque les wimps sont devenus gravitationnellement liés dans les halos galactiques. De plus, le taux d’annihilation est
renforcé à l’intérieur d’objets matériels comme le Soleil ou la Terre. Cela se passe car
il est possible que les wimps soient piégés à l’intérieur de tels objets si, en traversant
l’objet, le wimp subit une collision élastique avec un noyau (Figure 2.16). Si la diﬀusion donne au wimp une vitesse ﬁnale plus faible que la vitesse d’échappement dans
l’objet, le wimp va se trouver sur une orbite qui passe au travers de l’objet. Après
une succession de collisions, le wimp va se trouver thermalisé dans le cœur. Dans le
cas de la matière noire supersymétrique, le taux de piégeage dans le Soleil est suﬃsamment élevé pour que la concentration en wimps atteigne un état stationnaire où
le piégeage est équilibré par soit l’annihilation (pour les wimps de grande masse) ou
par évaporation (pour ceux de faible masse). Dans le cas du Soleil, la frontière entre
faible et forte masse est ∼ 3 GeV.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
La matière noire
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
χ
shielding
χ
nuclear
recoil
sensor
ÉC
E
L
O
T
Y
L
PO
β
83
N
H
EC
E
U
IQ
Compton
electron
γ
γ
radioactive
impurity
Fig. 2.15: Schéma d’un détecteur « calorimétrique » de wimps entouré de son blindage. Le
wimp galactique χ entre dans le détecteur, diﬀuse sur un noyau, et quitte le détecteur. Le
noyau de recul crée des excitations secondaires (de la lumière de scintillation, de l’ionisation,
des phonons) qui sont détectées par le capteur. Également représenté, un événement du bruit
de fond dû à la radioactivité ambiante, qui crée un électron Compton dans le détecteur.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
84
χ
ÉC
E
U
IQ
Chapitre 2. Cosmologie observationnelle
E
L
O
T
Y
L
PO
χχ
N
H
EC
µ
χ
ν
ν +X
χ
χ
χ
ν
π
µ
χ
p
N
H
EC
E
U
IQ
Fig. 2.16: Capture d’un wimp χ dans la Terre. Si le wimp perd suﬃsamment d’énergie dans
T
Y
L
PO
une collision avec un noyau, sa vitesse tombe sous la vitesse d’échappement, ce qui le met sur
une orbite passant par la Terre. Les collisions suivantes thermalisent le wimp au centre de la
Terre. L’annihilation avec un anti-wimp thermalisé mène à la production de neutrinos que
l’on peut détecter à la surface. Comme on l’indique, le bruit de fond pour de tels événements
provient des neutrinos produits par la désintégration de mésons π et K produits par les rayons
cosmiques dans l’atmosphère terrestre.
ÉC
E
L
O
Les seuls produits d’annihilation que l’on peut voir sortir de la Terre ou du Soleil
sont, bien entendu, des neutrinos . Le ﬂux de tels neutrinos peut se calculer, pour
un candidat wimp donné, et se ﬂux peut être comparé à celui observé par des détecteurs souterrains. Le ﬂux observé est complètement expliqué par la désintégration
des mésons π et K cosmiques dans l’atmosphère terrestre (Fig. 2.16). Certains wimps
supersymétriques pourraient donner des ﬂux supérieurs, ils sont donc exclus [69, 70].
U
Q
I
N
Puisque le ﬂux observé de neutrinos est sujet à un bruit de fond inévitable, la seule
amélioration des limites de telles techniques ne peut provenir que de l’observation d’un
petit excès de neutrinos provenant de la direction du Soleil ou du centre de la Terre.
La méthode la plus raisonnable serait de chercher des muons se propageant vers le
haut et provenant d’interactions de νµ dans la roche au dessous d’un détecteur. Les
calculs [71] indiquent qu’un détecteur de 1 km2 avec un seuil en énergie des muons de
∼ 10 GeV serait nécessaire pour observer un signal solaire statistiquement signiﬁcatif
pour de la matière noire supersymétrique typique. Des eﬀorts sont faits dans cette
direction en équipant la Méditerranée [72] et les glaciers du continent antarctique [73]
aﬁn d’observer la lumière Cherenkov produite par des muons.
ÉC
E
L
O
Y
L
PO
H
C
TE
E
La matière noire
4.2
Les axions
T
Y
L
PO
N
H
EC
E
U
IQ
85
Les axions [74] sont des particules scalaires légères hypothétiques qui ont été inventées pour empêcher la violation de CP dans les interactions fortes 7 . Ils auraient
été produits dans l’univers primordial à la fois par des mécanismes thermiques et des
mécanismes non-thermiques et pourraient produire des densités restantes proches de
la criticité si leur masse est dans la gamme ma ∼ 10−5 eV à ∼ 10−3 eV. Les axions se
comportent comme de la matière noire froide et devraient être présents dans le halo
galactique.
La méthode de détection la plus en vogue pour les axions galactiques repose sur le
couplage d’un axion à deux photons [75] ce qui permet à l’axion de se « convertir »
en un photon de fréquence ν = ma c2 /h en présence d’un champ magnétique. Si l’on
accorde une cavité micro-ondes à cette fréquence, les axions se manifestent par un
excès d’absorption de puissance (par rapport aux fréquences voisines). Si le halo est
dominé par des axions, la puissance prévue est faible, de l’ordre de 10−21 W pour
une cavité d’un volume de 3 m3 et pour un champ magnétique de 10 T. Comme la
masse de l’axion est inconnue, il est nécessaire de balayer toute la gamme de fréquences
intéressante. Des expériences-pilotes [76, 77] ont donné des limites sur la densité locale
d’axions d’un facteur 30 supérieur à la densité attendue. De nouvelles expériences sont
en cours pour chercher des axions au niveau de sensibilité requis [78].
ÉC
4.3
E
L
O
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
Matière noire baryonique
ÉC
La théorie de la nucléosynthèse primordiale aﬃrme que la densité baryonique est
environ 0.04 fois la densité critique, ce qui laisse à penser que les baryons ne peuvent
pas rendre compte de toute la matière noire. Il est néanmoins possible que des baryons
composent la matière noire galactique s’ils sont sous une forme qui n’émet ni n’absorbe
de lumière de façon signiﬁcative. Les diverses possibilités ont été passées en revue dans
[79]. La façon la plus simple de cacher des baryons est de les placer dans des objets
compacts qui soit ne brûlent pas (par exemple des naines brunes) ou ont cessé de
brûler (par exemple des naines blanches, des étoiles à neutrons, des trous noirs). Les
naines brunes ont une masse < 0.07M ce qui les rend trop froides pour brûler de
l’hydrogène. À l’origine, elles étaient les candidates favorites parce qu’elles évitent
complètement les contraintes reposant sur la production d’un fond de lumière ou
la pollution du milieu interstellaire par des éléments lourds par perte de masse ou
explosions de supernovae [80].
Les objets sombres qui se trouvent dans les halos galactiques sont appelés des
« machos », pour « massive compact halo objects ».
Paczyński [81] a proposé que les machos pouvaient être découverts au travers de
l’eﬀet de lentille gravitationnelle d’étoiles individuelles du Grand Nuage de Magellan
(LMC) (Fig. 2.17). Cette petite galaxie se trouve à 50 kpc de la Terre.
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
7 Une telle violation donnerait un moment électrique dipolaire permanent au neutron qui violerait
les limites expérimentales actuelles [21].
ÉC
E
86
ÉC
E
U
IQ
Chapitre 2. Cosmologie observationnelle
E
L
O
T
Y
L
PO
N
H
EC
Milky Way
ÉC
E
L
O
T
Y
L
PO
N
H
EC
dark deflector
E
U
IQ
LMC
star
SMC
Fig. 2.17: Schéma d’un eﬀet de lentille gravitationnelle dans le Grand Nuage de Magellan
(LMC) par un objet invisible du halo galactique. Alors que les deux images ne peuvent pas
être résolues aisément, la lumière combinée de ces deux images donne lieu à une ampliﬁcation
temporaire de la lumière de l’étoile lorsque l’objet invisible passe au voisinage de la ligne de
visée. La courbe de lumière d’une source ponctuelle est montrée sur la ﬁgure 2.18.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
La matière noire
T
Y
L
PO
N
H
EC
E
U
IQ
87
La théorie de l’eﬀet de lentille gravitationnelle sera présentée dans la section 8.
Dans le cas du « lensing »8 par des objets stellaires du halo galactique, l’angle entre
les deux images est très petit ( < 1 milliarcsec). Ce type de lentille est donc appelé
« microlensing ». Les télescopes terrestres ne peuvent pas résoudre les deux images
car la turbulence atmosphérique brouille les images et que les objets stellaires ont une
dimension angulaire de l’ordre de 1 arcsec. Le seul eﬀet observable est par conséquent
une ampliﬁcation passagère de l’intensité totale lorsque le macho se rapproche de la
ligne de visée, puis s’en éloigne. L’ampliﬁcation est
ÉC
E
L
O
A =
u2 + 2
√
,
u u2 + 4
(2.17)
où u est la distance la plus proche de la ligne de visée (non-déﬂéchie)
à laquelle passe
le déﬂecteur en unités du « rayon d’Einstein » RE = 4GM Lx(1 − x)/c2 où L est
la distance source–observateur, Lx est la distance observateur–déﬂecteur, et M est la
masse du macho.
L’ampliﬁcation est supérieure à 1.34 lorsque la distance à la ligne de visée est
inférieure à RE . Cette ampliﬁcation correspond à un seuil d’observation raisonnable
puisque la photométrie peut être eﬀectuée aisément à mieux que 10%. À un certain instant, la probabilité P qu’une étoile soit ampliﬁée par plus d’un facteur 1.34
est simplement la probabilité que sa lumière non-déﬂéchie passe à moins d’un rayon
d’Einstein d’un macho :
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
2
P ∼ nmacho L πRE
,
(2.18)
où nmacho est le nombre volumique moyen de machos entre le LMC et nous, et L est
la distance du LMC. La densité de machos est environ nmacho ∼ Mhalo /M L3 où Mhalo
est la masse totale du halo jusqu’à la position du LMC. En utilisant l’expression du
rayon d’Einstein, on trouve que P ne dépend pas de la masse M mais est seulement
déterminée par la vitesse du LMC :
P ∼
2
GMhalo
vLMC
∼
.
Lc2
c2
(2.19)
On pense que le LMC est en orbite autour de la Voie Lactée avec une vitesse de
vLMC ∼ 200 km s−1 (ce qui correspond à une courbe de rotation plate jusqu’au LMC).
Dans ce cas, P est de l’ordre de 10−6 . Des calculs plus détaillés donnent P = 0.5×10−6
[82].
Puisque l’observateur, l’étoile et le déﬂecteur sont en mouvement relatif, une ampliﬁcation notable ne dure que tant que le rayon non déﬂéchi demeure à l’intérieur du
rayon d’Einstein. La courbe de lumière résultante, qui est achromatique et symétrique,
est représentée pour une série de valeurs du paramètre d’impact sur la ﬁgure 2.18.
L’échelle de temps de l’ampliﬁcation est le temps ∆t mis par l’objet pour traverser
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
8 Pour des raisons de concision, nous gardons le terme anglais pour la focalisation et les autres
eﬀets d’optique gravitationnelle.
ÉC
E
88
E
U
IQ
Chapitre 2. Cosmologie observationnelle
N
H
EC
STANDARD MICROLENSING LIGHT CURVE
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
Fig. 2.18: Courbes de microlensing pour une source ponctuelle. Les courbes correspondent à
4 valeurs de la distance d’approche minimale (0.5, 0.7, 1.0 et 1.5 rayon d’Einstein). L’échelle
de durée ∆t , qui dépend de la masse, est normalisée selon (2.20).
T
Y
L
PO
un rayon d’Einstein entre l’observateur et la source. S’agissant d’étoiles du LMC et
de déﬂecteurs de notre halo, les vitesse relatives sont de l’ordre de 200 km s−1 et la
position du déﬂecteur est grosso modo à mi-chemin entre l’observateur et la source
(x ∼ 0.5). Le ∆t moyen est alors
RE
M
∆t ∼
∼ 75 jours
.
(2.20)
200 km s−1
M
ÉC
E
L
O
La distribution en durée peut donc servir pour estimer la masse des machos en supposant qu’ils sont dans le halo galactique (et non dans le LMC).
Deux groupes expérimentaux, la collaboration MACHO et la collaboration EROS,
ont publié les résultats de recherches d’événements dans la direction du LMC et du
SMC (le Petit nuage de Magellan voisin). L’absence d’événements de durée inférieure
à 15 jours a permis aux deux groupes d’exclure les objets de masse dans la plage
10−7M < M < 10−1 M [83] comme composante principale du halo. Ces limites
excluent les naines brunes de masse ∼ 0.07M comme composantes importantes du
halo.
La collaboration MACHO a toutefois observé 13 événements d’une durée moyenne
de ∼ 50 jours [84]. Si on les interprète comme provenant de lentilles sombres du halo
galactique, le taux correspond à une fraction f = 0.2 de machos contribuant à la
masse totale du halo. L’échelle de temps correspond à des objets de masse ∼ 0.4M
(ﬁgure 2.19).
EROS n’a publié que des limite supérieures sur la fraction du halo qui est composée
de machos [85], comme on le montre sur la ﬁgure 2.19.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
La matière noire
T
Y
L
PO
N
H
EC
E
U
IQ
89
Les résultats des deux expériences démontrent qu’il est peu vraisemblable que le
halo soit formé entièrement d’objets de masse stellaire. Le déﬁ actuel est de démontrer
que les événements observés par la collaboration MACHO sont bien dus au lensing
par des objets du halo et non, par exemple, par du lensing d’objets dans les nuages
eux-mêmes. Si cela peut être prouvé, l’estimation de la masse suggèrerait qu’il s’agit
de très vieilles naines blanches, peut-être les premières étoiles.
ÉC
E
L
O
L’information sur la localisation des lentilles (halo galactique ou Nuages de Magellan) est très diﬃcile à obtenir. Le cas le plus facile est celui d’événements de grande
ampliﬁcation, notamment les événements dus à des lentilles binaires. Dans de tels
événements, la courbe de lumière est modiﬁée d’une façon qui dépend des distances
relatives de la lentille et de l’étoile source [86]. Il est également possible d’obtenir de
l’information sur la distance de la lentille dans des événements de très longue durée
où le mouvement de la Terre autour du Soleil modiﬁe la courbe de lumière [87]. Dans
le futur, on pourra aussi résoudre tout juste les deux images de microlensing avec
des téléscopes interférentiels spatiaux. De telles observations donneront suﬃsamment
d’information pour déterminer la distance des lentilles et trancher.
T
Y
L
PO
N
H
EC
E
U
IQ
Des recherches d’objets sombres par microlensing sont en cours dans la galaxie
spirale voisine M31 [88].
E
L
O
Une deuxième façon de cacher des baryons dans les halos galactiques est de les
mettre dans de petits nuages de gaz froid composés d’hélium primordial et d’hydrogène moléculaire [32]. Pour passer inaperçu en raie de 21 cm de l’hydrogène atomique,
l’hydrogène doit être sous forme moléculaire. Le gaz doit être dans des nuages car un
gaz uniformément réparti dans l’espace produirait une absorption des sources extragalactiques dans les transitions moléculaires que l’on n’a pas observée [89]. Des nuages
de densité suﬃsante seraient suﬃsamment rares pour qu’il n’y ait pas d’absorption le
long de la plupart des lignes de visée.
ÉC
Cette idée est très eﬃcace pour cacher les gaz, mais elle est très controversée quant
à la plausibilité que de telles quantités de molécules puissent avoir été fabriquées.
Dans les disques galactiques, on pense que les molécules se forment principalement à
la surface de grains de poussière, ce qui ne peut se produire dans un mélange gazeux
primordial.
H
C
TE
U
Q
I
N
Des limites sur la quantité de nuages froids de gaz moléculaire on été obtenues
à partir du ﬂux de photons de haute énergie qui seraient produits par l’interaction
des rayons cosmiques avec les nuages [90]. Les limites sur la proportion dans le halo
sont plus diﬃciles à déterminer. Dans certaines conditions, les nuages moléculaires
pourraient être observables dans des explorations par microlensing, soit dans notre
galaxie en utilisant les nuages de Magellan [91] ou dans des Amas de galaxies en
utilisant les quasars du fond du ciel [92].
ÉC
E
L
O
Y
L
PO
E
90
ÉC
E
U
IQ
Chapitre 2. Cosmologie observationnelle
E
L
O
T
Y
L
PO
N
H
EC
Excluded by EROS at 95% CL
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
Permitted
by MACHO
at 95% CL
Fig. 2.19: Contraintes de microlensing sur la fraction de masse du halo galactique total
U
Q
I
N
contenue dans les machos (en unités M ). La ﬁgure montre la limite supérieure obtenue par
EROS [85] dans la recherche de microlensing en direction des nuages de Magellan ainsi que
la région permise par MACHO [84] autour d’une fraction de masse de ∼ 0.2 et une masse
de ∼ 0.5M .
ÉC
E
L
O
Y
L
PO
H
C
TE
E
Les paramètres cosmologiques
5
5.1
N
H
EC
E
U
IQ
91
Les paramètres cosmologiques
H0
E
L
O
T
Y
L
PO
Le taux actuel d’expansion H0 , joue un rôle multiple en cosmologie. Son inverse,
le temps de Hubble tH , est l’échelle de temps de l’expansion qui donne l’ordre de
grandeur du temps écoulé depuis le début de l’époque actuelle d’expansion classique :
ÉC
t0 = H0−1 f (ΩM , ΩΛ ) ,
(2.21)
où la fonction f (ΩM , ΩΛ ) tient compte de l’accélération ou de la décélération de
l’expansion ; elle sera calculée au chapitre 5. La distance de Hubble dH = c H0−1 donne
l’échelle de l’horizon classique actuel et la relation entre la distance et le redshift des
galaxies proches
R = c H0−1 z
z1.
H0 détermine la densité critique
LY T
3H02
ρc =
.
8πG
O
P
E
L
ÉCO
N
H
EC
E
U
IQ
(2.22)
(2.23)
Dans un univers avec ΩΛ = 0, la densité critique détermine la frontière entre des univers qui continueront leur expansion éternellement et des univers qui se contracteront.
Enﬁn, comme nous le verrons dans la section suivante, H0 entre dans la détermination des densités universelles de plusieurs façons, et cette constante est nécessaire pour
comparer les densités. Par exemple, la densité de photons est mesurée directement ce
qui donne ργ ∝ Ωγ H02 . La théorie de la nucléosynthèse primordiale permet de déterminer le rapport baryon/photon, par conséquent on connaît également ρb ∝ Ωb H02 .
D’un autre côté, les observations de l’anisotropie du CBR et des supernovae de grand
redshift donne directement ΩM et ΩΛ . Toute conclusion sur les valeurs relatives de
ΩM et Ωb et, par conséquent, l’importance de la matière noire non-baryonique dépend
de la valeur de H0 .
La valeur de H0 se déduit de la loi de Hubble
v = H0 R ,
(2.24)
U
Q
I
N
où v est la vitesse de récession d’une galaxie (que l’on détermine aisément à partir du
déplacement vers le rouge (redshift) des raies spectrales de cette galaxie) et R est la
distance de la galaxie. La loi s’applique dans l’intervalle de vitesses 10−2 c < v < 10−1 c,
la limite inférieure étant nécessaire pour pouvoir négliger la vitesse particulière et la
limite supérieure pour pouvoir négliger les corrections relativistes qui dépendent de
q0 .
La diﬃculté première dans la détermination de H0 provient de la diﬃculté de
la détermination des distances des galaxies. Les diverses méthodes peuvent grosso
modo être rangées en deux catégories, les méthodes « astrophysiques » qui sont
ÉC
E
L
O
Y
L
PO
H
C
TE
E
92
E
U
IQ
Chapitre 2. Cosmologie observationnelle
T
Y
L
PO
N
H
EC
calibrées avec l’étalonnage des distances, et les méthodes « physiques » qui donnent
directement les distances des galaxies.
La plupart des déterminations astrophysiques de distances utilisent des chandelles
standard de luminosité L connue. Le ﬂux provenant d’une chandelle à la distance R
est φ = L/4πR2, par conséquent la mesure du ﬂux donne la distance. Pour les galaxies
suﬃsamment lointaines pour être utilisées dans la détermination de H0 , les seuls objets
suﬃsamment brillants sont les supernovae et les galaxies elles-mêmes. Comme nous
l’avons vu dans la section 1, les supernovae de type Ia ont des luminosités maximales
relativement uniformes (Figure 2.8) ce qui en fait des chandelles standard utiles [93].
On peut également estimer la luminosité d’une galaxie par des lois empiriques qui
relient la luminosité à la dispersion en vitesse, comme la relation de Tully–Fisher
pour les galaxies spirales (Fig. 2.11).
La relation de Tully–Fisher et la luminosité des supernovae doivent être calibrées
à partir de galaxies proches (ou des supernovae qu’elles contiennent) de distance
connue. La meilleure méthode pour déterminer les distances des galaxies proches
consiste à utiliser les étoiles variables Céphéides dont la relation entre leur luminosité
et leur période est connue (Section 1). L’excellent résolution angulaire du Hubble
Space Telescope a permis de résoudre des Céphéides dans des galaxies jusqu’à environ
30 Mpc. À ce jour, les distances de vingt galaxies ont été ainsi déterminées, dont sept
ont hébergé des supernovae de type Ia.
L’étalonnage le plus précis de la relation période-luminosité des Céphéides utilise
les Céphéides du Grand Nuage de Magellan (Fig. 2.5). Cette méthode d’étalonnage
demande de connaître la distance du LMC. On peut aussi calibrer à l’aide de Céphéides
dans des amas d’étoiles dans la Voie Lactée (ce qui demande de connaître la distance
de ces groupes) ou bien directement, grâce au petit nombre de Céphéides dont les
distances on été mesurées directement par parallaxe par le satellite Hipparcos.
La précision de l’étalonnage par les Céphéides du LMC est limitée par notre
connaissance de la distance du LMC. Plusieurs méthodes peuvent être utilisées pour
cette mesure. Certaines utilisent des objets stellaires calibrés par parallaxe (Section 1)
D’autres sont des méthodes physiques qui donnent des mesures directes (voir par
exemple l’exercice 2.9). Toutes ces méthodes donnent des valeurs de la distance du
LMC qui diﬀèrent entre elles de ∼ ±10% [51, 21].
À partir des supernovae de type Ia, le Hubble Space Telescope Key Project sur
l’échelle extragalactique donne [94]
ÉC
E
L
O
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
H0 = 68 ± 2 (statistique) ± 5 (systématique) km s−1 Mpc−1 ,
H
C
TE
alors qu’avec la relation de Tully–Fisher il donne [95]
H0 = 71 ± 4 (statistique) ± 7 (systématique) km s−1 Mpc−1 ,
Y
L
PO
U
Q
I
N
(2.25)
(2.26)
(voir toutefois [96]). Les erreurs systématiques (corrélées) proviennent des échelons de
l’étalonnage des distances ; la moitié est due à la distance du LMC. Les deux valeurs
de H0 sont compatibles avec d’autres méthodes astrophysiques utilisées par le HST
key project [97].
ÉC
E
L
O
E
Les paramètres cosmologiques
T
Y
L
PO
R
ÉC
E
L
O
N
H
EC
E
U
IQ
93
D=2vt
θ
v
Fig. 2.20: Photosphère d’une supernova en expansion à la vitesse v. La vitesse peut être
déduite de la position et de la forme des raies spectrales. Connaissant l’instant de l’explosion
texp on peut déduire le diamère D = 2v(t − texp ). L’angle θ peut être estimé en utilisant la
loi de Stefan, ce qui permet d’estimer la distance R.
T
Y
L
PO
N
H
EC
E
U
IQ
Trois méthodes « physiques » permettent de court-circuiter l’étalonnage des distances. La première est la méthode de la « photosphère en expansion » (EPM) appliquée aux supernovae de type II (Section 1). Après l’explosion initiale, la surface
(photosphère) du cœur se dilate à une vitesse v ∼ 10−2 c, comme on le voit sur la ﬁgure
2.20. La vitesse peut être déterminée empiriquement à partir des déplacements Doppler des raies du spectre de la supernova. La connaissance de l’instant de l’explosion tsn
permet alors de calculer le diamètre physique de la photosphère D = 2v(t − tsn ). Si la
taille angulaire ∆θ était connue, la distance de la supernova pourrait être déterminée
directement par la relation R = 2v(t − tsn )/∆θ. Pour les supernovae extragalactiques,
la taille angulaire est trop faible pour être mesurée directement mais on peut l’estimer
à partir du ﬂux lumineux mesuré, en utilisant la loi de Stefan (2.1), modiﬁée de façon
appropriée pour tenir compte de ce que la photosphère n’est pas exactement un corps
noir. Cette technique mène à une valeur de H0 = 73 ± 15 km s−1 Mpc−1 [98].
La seconde méthode physique utilise le décalage temporel entre deux images du
même quasar subissant un eﬀet de mirage sous l’eﬀet d’amas de galaxies intermédiaires. Trois exemples de quasars ayant subi des eﬀets de lentille gravitationnelle
ont été trouvés pour lesquels la variabilité intrinsèque du quasar permet la mesure
du décalage temporel. Comme les chemins optiques sont proportionnels à l’échelle de
distance et par conséquent à c/H0 , le décalage temporel entre les deux images est
proportionnel à c/H0 . La constante de proportionnalité sera calculée au chapitre 3 en
section 8. Elle dépend de la séparation angulaire des deux images et de la distribution de masse de la lentille. Cette distribution de masse peut être évaluée à partir de
la distribution d’arcs gravitationnels provenant de la lumière de galaxies au delà la
lentille. La connaissance de cette distribution met une limite sur la précision de cette
méthode. Les auteurs conservateurs donnent une valeur H0 = 60 ± 20 km s−1 Mpc−1
[99].
ÉC
E
L
O
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
94
E
U
IQ
Chapitre 2. Cosmologie observationnelle
T
Y
L
PO
N
H
EC
La dernière méthode physique utilise l’eﬀet Sunyaev–Zel’dovich (SZ) qui fait que
les photons du fond cosmique CBR sont chauﬀés par diﬀusion Compton sur le gaz
chaud ionisé d’un amas de galaxies (Fig. 2.21). Le spectre du CBR se trouve déformé
dans la direction de l’amas en proportion de la probabilité de diﬀusion dans l’amas :
ÉC
E
L
O
P ∼ ne σT D = ne σT R∆θ ,
(2.27)
où ne est la densité moyenne d’électrons dans l’amas, σT est la section eﬃcace
Thomson, et D = R∆θ est le diamètre de l’amas à une distance R telle que l’angle
sous-tendu soit ∆θ. Pour un amas, ∆θ peut être observé directement, et si P est
mesuré par eﬀet SZ, il suﬃt d’estimer ne pour determiner R.
La densité d’électrons peut être estimée au travers de la luminosité de l’amas en
rayons X qui est (exercice 2.11)
LX ∼ c2 n2e ασT me T D3 ,
(2.28)
où α est la constante de structure ﬁne. Il s’ensuit que
n2e ∼
N
H
EC
4πφx
.
cασT ∆θ3 R3
T
Y
L
PO
E
U
IQ
(2.29)
En combinant (2.27) et (2.29), on obtient la distance de l’amas :
√
P 2 cα∆θ me T n2e R ∼
.
4πφx σT
ne 2
ÉC
E
L
O
(2.30)
Toutes les quantités du membre de droite peuvent être mesurées sauf n2e /ne 2 . Ce
facteur est de l’ordre de l’unité si le gaz est relativement uniforme. Une non-uniformité
produirait une surestimation de R et, par conséquent, une sous-estimation de H0 . On
doit aussi supposer que l’amas est sphérique, bien que cette hypothèse puisse être
éliminée en moyennant les mesures faites sur plusieurs amas. Une détermination de
H0 par cette méthode a donné [100]
H0 = (54 ± 14) km s−1 Mpc−1 ,
(2.31)
où pratiquement toute l’erreur estimée est due aux eﬀets systématiques évoqués cidessus. Avec l’augmentation du nombre d’amas étudiés, les astronomes pourront
mieux estimer et contrôler les incertitudes de cette méthode prometteuse.
5.2
Les diverses densités ρ et Ω
H
C
TE
U
Q
I
N
Nous donnons ici un résumé des méthodes utilisées pour déterminer les valeurs
actuelles des densités universelles données dans la table 1.1.
La seule densité cosmologique qui soit directement mesurée est la densité de photons avec la mesure de COBE [22] de la température du fond cosmique de photons
CBR, qui donne :
ÉC
E
L
O
Y
L
PO
ργ = (2.61 ± 0.01) × 105 eV m−3
−5
⇒ Ωγ = 5.16 h−2
.
70 × 10
(2.32)
E
Les paramètres cosmologiques
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
95
CBR
e−
ÉC
E
L
O
T
Y
L
PO
N
H
EC
p
E
U
IQ
D
e−
Fig. 2.21: Un amas de galaxies de diamètre D. Les photons du CBR peuvent étre diﬀusés
par les électrons libres du gaz chaud ionisé de l’amas, ce qui augmente l’énergie moyenne
des photons du CBR qui parviennent de la direction de l’amas (eﬀet SZ). Le gaz ionisé émet
aussi des rayons X via le bremsstrahlung thermique d’électrons se diﬀusant sur des protons
et des noyaux.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
96
E
U
IQ
Chapitre 2. Cosmologie observationnelle
T
Y
L
PO
N
H
EC
Les mesures des autres densités tombent dans deux catégories : les mesures qui concernent le rapport d’une densité avec celle des photons et les mesures qui ne le sont pas.
Dans la première catégorie on trouve
ÉC
E
L
O
– Neutrinos. Les calculs thermodynamiques du chapitre 6 donnent nν = (3/11)nγ
pour chaque espèce de neutrinos. La densité actuelle de neutrinos dépend alors
des masses des neutrinos avec (1.33) pour des neutrinos de masse nulle (mν Tγ (t0 ) = 2.349 × 10−4 eV) et (1.34) pour des neutrinos massifs. Notons que le
même type de calcul donnera le nombre volumique de toute espèce de particule
massive interagissant faiblement s’il n’y a pas d’asymétrie particule-antiparticule.
– Baryons. La théorie de la nucléosynthèse primordiale prévoit l’abondance des
éléments légers en fonction du rapport baryon/photon η = nb /nγ . Les abondances observées [24] impliquent η = (5 ± 1) × 10−10 qui donne Ωb = (0.04 ±
0.01) h−2
70 (1.22).
E
U
IQ
– Matière non relativiste. Le rapport de la masse baryonique à la masse totale a
−3/2
été estimé dans les amas de galaxies à ∼ 0.12 h70 ( 2.13). Cette estimation
suppose que toute la masse baryonique est sous la forme de gaz chaud intergalactique ou de galaxies visibles. En supposant que c’est le cas, on peut estimer
ΩM /Ωb en supposant que le rapport baryon sur masse totale dans les amas est
égal à la valeur universelle :
ÉC
E
L
O
T
Y
L
PO
ΩM =
Ωb
0.12
−3/2
h70
N
H
EC
−1/2
= 0.33 h70
,
(2.33)
où nous avons utilisé la valeur de Ωb calculée à partir de la valeur du rapport
baryon/photon donné par la nucléosynthèse. Étant donné le nombre d’hypothèses qui entrent dans la détermination de ce nombre, on hésite à lui attribuer
une incertitude. Notons que l’universalité supposée pour le rapport baryons sur
total est conﬁrmée par les simulations numériques de la formation de structures
[101].
Les autres méthodes de détermination des densités cosmologiques demandent des
concepts qui seront développés dans les chapitres 5 et 7. Elles sont résumées dans la
Table 2.3. Donnons ici un avant goût de ce qui va suivre.
ΩM peut être estimé au travers de son inﬂuence sur la formation de structures.
La méthode la plus simple de ce genre est l’évolution du nombre d’amas de galaxies
avec le temps ou, de façon équivalente, avec le redshift [102]. Comme indiqué en
Sect. 2.6, les structures peuvent se former à partir de petites ﬂuctuations de densité
seulement si l’univers est dominé par de la masse avec une densité proche de la densité
critique. Si cette condition est satisfaite, une région de petite sur-densité agit comme
un mini-univers fermé qui, à un moment, se détachera de l’expansion pour former une
structure virialisée. Si ΩM ∼ 1 des structures se forment encore aujourd’hui, alors
que si ΩM 1 la formation de structures a eu lieu seulement dans le passé lorsque la
densité de masse était proche de la valeur critique. Cet eﬀet devrait être visible sur le
nombre d’amas en fonction du redshift, une dépendance importante étant un signal
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Les paramètres cosmologiques
T
Y
L
PO
N
H
EC
E
U
IQ
97
Tab. 2.3: Quelques méthodes de détermination des paramètres de densité cosmologiques. La
plupart des mesures de ΩM sont compatibles avec ΩM = 0.3 ± 0.1.
E
L
O
quantité
ÉC
ΩM
méthode
référence
proportion de baryons dans les amas
Chap.2, sect. 5.2, exercice 2.7
masse-luminosité dans les amas
Chap. 2, exercice 2.7
spectre des ﬂuctuations de densité
Chap. 7, sect. 2
évolution du nombre d’amas
Chap. 7, sect. 2
ﬂots globaux, vitesses particulières
Chap. 7, sect. 2
q0
diagramme de Hubble des SN
ΩT
anisotropies du CBR
ÉC
E
L
O
T
Y
L
PO
N
H
EC
Chap. 5, sect. 2
E
U
IQ
Chap. 5, sect. 2, et 7 sect.9
que ΩM ∼ 1. Une énergie du vide non-nulle complique l’analyse mais l’évolution des
amas donne tout de même une valeur relativement appréciable pour ΩM . Une étude
récente [103] donne ΩM = 0.49 ± 0.12 pour ΩΛ = 0 et ΩM = 0.44 ± 0.12 pour ΩT = 1.
Aux échelles supra-amas, ΩM est l’un des paramètres qui déterminent la forme
du spectre de puissance des ﬂuctuations de densité. Les structures à grande échelle
de l’univers peuvent être caractérisées en eﬀectuant la décomposition de Fourier
du contraste de densité en modes de longueur d’onde comobile λ = 2πâ(t)/k où
k est le nombre d’onde considéré. Dans la formation de structures avec de la matière noire froide et des ﬂuctuations de densité primordiales adiabatiques, les modes
de petite longueur d’onde voient leur amplitude atténuée parce que ces modes oscillent comme des ondes acoustiques pendant l’époque de rayonnement alors que
l’amplitude des modes de grande longueur d’onde a cru à la fois pendant l’époque
du rayonnement et pendant celle de la matière. La démarcation entre longueurs
d’ondes courtes et longues correspond à la distance de Hubble au moment de l’égalité
matière-rayonnement, a(teq ) = a0 1.68Ωγ /ΩM et à une longueur d’onde actuelle de
λeq ∼ 14 h−1
70 Mpc/(ΩM h70 ).
Les modes plus courts que λeq doivent avoir une amplitude atténuée par rapport
à l’amplitude extrapolée des modes de grande longueur d’onde. Puisque λeq dépend
de ΩM , on peut estimer ΩM à partir du spectre de puissance. Les ﬂuctuations dans la
température du CBR donnent l’amplitude à grande échelle alors que les corrélations
de galaxies donnent l’amplitude aux plus petites échelles. On sait depuis plus de 10
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
98
E
U
IQ
Chapitre 2. Cosmologie observationnelle
T
Y
L
PO
N
H
EC
ans que le spectre de puissance favorise les valeurs de ΩM inférieures à un. Dans une
évaluation récente [104], l’accent a été mis sur le fait qu’aucun modèle ne rend bien
compte de la corrélation des galaxies et des données sur l’anisotropie du CBR, bien
que les modèles avec ΩM ∼ 0.3 fassent mieux que ceux avec ΩM ∼ 1.
En résumé, il apparaît que la plupart des auteurs s’accordent sur le fait qu’un
univers critique ne contenant que de la matière est en désaccord avec les données
ÉC
E
L
O
0.2 < ΩM < 0.7 .
(2.34)
On peut espérer que de meilleures mesures de redshift et des études d’eﬀets faibles
de lentille gravitationnelle par les structures à grande échelle clariﬁeront la situation.
Les estimations de ΩM peuvent être combinées avec une mesure du paramètre
de décélération q0 = ΩM /2 − ΩΛ pour estimer ΩΛ . Pour l’instant, la façon la ﬁable
pour mesurer q0 passe par l’utilisation des supernovae de type Ia comme chandelles
standard. Nous verrons dans la section 5 que, pour un redshift donné, la distance
des objets est une fonction décroissante de q0 (voir la Fig. 3.10). Cela résulte en une
luminosité moyenne apparente des supernovae qui est une fonction croissante de q0 .
Deux équipes [26, 27] ont observé que les ﬂux de supernovae à z ∼ 0.5 sont à peu
près 20% plus faibles que ce que l’on attend dans un univers marginalement décéléré
avec ΩM = 0.3 et ΩΛ = 0 (Fig. 5.3). L’eﬀet peut être expliqué par un paramètre de
décélération de
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
q0 = −0.55 ± 0.2 .
(2.35)
Pour ΩM ∼ 0.3, cela correspond à
ΩΛ ∼ 0.7
si ΩM = 0.3 .
(2.36)
Bien entendu, les ﬂux faibles de supernovae pourraient être expliqués en supposant
que les supernovae typiques étaient moins lumineuses dans le passé que maintenant,
ou bien que 20% de la lumière est absorbé quelque part entre la supernova et nous.
L’hypothèse d’évolution peut être testée localement en observant des galaxies d’âge
eﬀectif diﬀérent, cet « âge eﬀectif » pouvant être donné par leur métallicité. Parce que
toute poussière absorbante serait chauﬀée dans ce processus, l’hypothèse d’absorption
peut être éliminée si le fond diﬀus infra-rouge peut être attribué à des sources discrètes
[105].
La somme des Ω mesurés individuellement donne ΩT ∼ ΩΛ + ΩM ∼ 1. On peut
maintenant mesurer directement ΩT au travers du spectre des ﬂuctuations de température du CBR. Nous verrons au chapitre 7 que le CBR a un spectre d’anisotropies
qui dépend de l’échelle angulaire, c’est-à-dire de la taille des pixels utilisés pour mesurer les variations de température. Plus précisément, notons T (θ, ∆θ) la température
observée dans le ciel dans la direction θ et moyennée sur un disque de rayon ∆θ dans
le ciel. La variance de cette quantité sur toutes les directions déﬁnit ∆T (∆θ). Les
observations par les expériences Boomerang [106] et Maxima [107] montrent un pic
de cette quantité pour ∆θ ∼ 1degré (ﬁgure 7.10).
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Exercices sur le chapitre 2
T
Y
L
PO
N
H
EC
E
U
IQ
99
Suivant une classe de modèles en vogue de formation des structures (des modèles
CDM avec des ﬂuctuations primordiales invariantes d’échelle et adiabatiques) l’échelle
où l’on s’attend à observer les plus grandes ﬂuctuations est celle qui correspond à la
distance de Hubble à la recombinaison. Nous verrons au chapitre 5 (ﬁgure 5.5) que la
taille angulaire correspondante dépend de ΩM et de ΩΛ avec ΩT = 1 ce qui correspond
à ∆θ ∼ 1 deg. Cela est en bon accord avec la valeur observée par les expériences
Boomerang et Maxima qui donnent [25]
ÉC
E
L
O
ΩT = 1.11 ± 0.07 .
(2.37)
Les expériences futures sur satellite [108] sur les anisotropies du CBR devraient mesurer cet Ω particulièrement important avec une très haute précision.
Exercices
E
U
IQ
10
2.1 La luminosité d’une galaxie typique est 2 h−2
70 × 10 L et l’énergie moyenne des
photons stellaires est ∼ 2 eV. Quel est le ﬂux de photons (en m−2 s−1 ) d’une galaxie
de redshift z (z 1 ⇒ R ∼ zdH ) ?
Comparer le ﬂux de photons provenant des plus proches galaxies voisines (R ∼
1 Mpc) avec le ﬂux de photons des étoiles les plus proches (R ∼ 1 pc). (Ce calcul doit
montrer pourquoi la plupart des objets visibles à l’œil nu sont des étoiles.)
ÉC
E
L
O
T
Y
L
PO
N
H
EC
2.2 La densité de luminosité de l’univers est ∼ 1.2 h70 108 L Mpc−3 . En supposant
que la production de lumière stellaire a été relativement constante depuis la formation
des premières étoiles, il y a un temps de Hubble, estimer le nombre de photons (E ∼
2 eV) qui ont été émis par les étoiles. Comparer le nombre de photons stellaires avec
le nombre de photons du CBR. (Ce problème sera traité de façon plus rigoureuse dans
l’exercice 5.12.)
L’énergie stellaire est produite principalement par la fusion de l’hydrogène en
hélium 4p → 4 He+2e+ +2νe. Cette transformation se produit dans les cœurs stellaires
par une suite de réactions qui libèrent au total ∼ 25 MeV. Après thermalisation,
l’énergie quitte la surface stellaire sous la forme de la lumière des étoiles. Estimer le
nombre de protons (par Mpc3 ) qui ont été transformés en hélium au cours du temps
de Hubble qui vient de s’écouler. Comparer ce nombre avec le nombre de protons
disponibles nb ∼ Ωb ρc /mp .
H
C
TE
U
Q
I
N
2.3 Estimer la contribution des processus suivants au libre parcours moyen universel
des photons :
Y
L
PO
– Diﬀusion Thomson des photons sur des électrons libres de nombre volumique
ne ∼ nb .
E
L
O
– Absorption par des étoiles de nombre volumique nétoiles ∼ Ωétoiles ρc /M, Ωétoiles ∼
2
.
0.003 et de section eﬃcace ∼ πR
ÉC
E
100
E
U
IQ
Chapitre 2. Cosmologie observationnelle
N
H
EC
– Absorption par la poussière des galaxies avec ngal ∼ 0.005 Mpc−3 de section
2
eﬃcace ∼ πRgal
, où Rgal ∼ 10 kpc et la fraction de lumière visible absorbée
dans le passage au travers d’une galaxie est ∼ 0.1.
E
L
O
T
Y
L
PO
Comparer ces distances avec dH (∼ la distance des objets visibles les plus lointains). L’univers est-il « transparent » ? (L’exercice 5.13 traitera ce problème plus
rigoureusement.)
ÉC
2.4 Identiﬁer les raies de la série de Balmer de l’hydrogène atomique (n = 2 → n )
dans le spectre de la ﬁgure 2.1.
La raie « Hβ » (n = 2 → n = 4) est observée dans les spectres galactiques de la
ﬁgure 2.9. Estimer les redshifts des deux galaxies.
E
U
IQ
2.5 En supposant qu’on ne peut mesurer que des redshifts, des angles et des ﬂux de
photons, expliquer les facteurs de h70 dans (2.8), (2.9) et (2.10) tout comme l’absence
de tels facteurs dans (2.11).
T
Y
L
PO
N
H
EC
2.6 En comparant la magnitude apparente des Céphéides du LMC (Fig. 2.5) à la
magnitude apparente des Céphéides de la galaxie NGC 1365 (Fig. 2.22) estimer le
rapport des distances de ces deux galaxies. Si on adopte comme distance du LMC
50 ± 5 kpc, quelle est la distance de NGC 1365.
NGC 1365 est un membre de l’amas de galaxies Fornax. La vitesse de récession
de cet amas est 1441 km s−1 . Estimer H0 .
ÉC
E
L
O
2.7 Les propriétés de l’amas Abell-496 on été étudiées dans [109].
(a) La vitesse de récession de A496 est 9885 km s−1 . Quelle est sa distance en fonction
de h70 ?
(b) La ﬁgure 2.23 montre la distribution angulaire des galaxies les plus brillantes de
l’amas A496. Estimer le rayon de cet amas.
(c) La ﬁgure 2.24 montre la distribution de vitesses de récession dans la direction
de l’amas A496. L’accumulation autour de 9885 km s−1 correspond aux membres
de l’amas. la largeur de cette accumulation suggère que la dispersion en vitesse de
A496 est ∆v ∼ 715 km s−1 . Utiliser le théorème du viriel pour estimer la masse de
l’amas : (GM/∆r ∼ ∆v 2 ). Une étude détaillée faite dans [109] donne Mvir = (5.1 ±
14
0.8)h−1
70 10 M .
(d) Le ﬂux de lumière visible venant de A496 indique que la luminosité totale est
12
L = 2.0 h−2
70 ×10 L . En supposant que Mvir /L est égal à la valeur universelle ρM /J0
avec une valeur de la densité universelle de luminosité donnée par (2.9), estimer ρM
et ΩM .
(e) Le spectre en rayons X indique que la température du gaz intergalactique dans
A496 est de 4 ± 1 keV. Le ﬂux de rayons X permet (exercice 2.11) d’estimer la masse
totale de l’amas et la masse totale de gaz intergalactique. Pour A496, la masse totale
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Exercices sur le chapitre 2
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
N
H
EC
101
E
U
IQ
Fig. 2.22: Magnitudes apparentes dans les bandes I et V des Céphéides de la galaxies NGC
1365 [30]. La magnitude est une fonction linéaire de log P où P est la période de la Céphéide
en jours.
E
L
O
T
Y
L
PO
−1
14
dans un rayon de 0.7 h−1
70 Mpc autour du centre de l’amas est (1.7 ± 0.4)h70 × 10 M
−5/2
et la masse totale de gaz dans la même région est (1.4 ± 0.5)h70 × 1013 M . En
supposant que le rapport entre la masse baryonique et la masse totale de A496 est
égal à la valeur universelle, estimer ΩM en adoptant la valeur de Ωb prévue par la
nucléosynthèse.
ÉC
2.8 La ﬁgure 2.25 montre les courbes de vitesse d’iso-récession de la galaxie NGC
5033 déduites du déplacement Doppler de la raie de 21 cm de l’hydrogène atomique.
Les courbes sont superposées à une image optique de la galaxie.
(a) Quel est le redshift de NGC 5033. En négligeant sa vitesse particulière, estimer
sa distance en fonction de h70 .
(b) Le rayon angulaire visible de NGC 5033 est d’à peu près 3 minutes d’arc. Quel
est le rayon visible en fonction de h70 ?
(c) Quelle est la vitesse de rotation loin du centre galactique ? On tiendra compte
de l’inclinaison de la galaxie et supposant qu’elle apparaîtrait comme circulaire si elle
était vue de face.
(d) Estimer la masse de NGC 5033 contenue dans 6 minutes d’arc du centre galactique
(en unités M et en fonction de h70 ).
(e) NGC 5033 a une magnitude apparente dans la bande V de 10.1. Quelle est sa
magnitude absolue et sa luminosité (en unités LV ) en fonction de h70 ? Quel est son
rapport masse-luminosité ?
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
102
ÉC
E
U
IQ
Chapitre 2. Cosmologie observationnelle
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
T
Y
L
PO
N
H
EC
E
U
IQ
U
Q
I
N
Fig. 2.23 : Distribution angulaire de galaxies brillantes dans A496 [109].
ÉC
E
L
O
Y
L
PO
H
C
TE
E
Exercices sur le chapitre 2
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
T
Y
L
PO
E
U
IQ
N
H
EC
103
E
U
IQ
U
Q
I
N
Fig. 2.24: Distribution des vitesses de récession dans la direction de l’amas A496 [109].
L’accumulation de 274 galaxies autour de 9885 km s−1 correspond aux membres de l’amas.
ÉC
E
L
O
Y
L
PO
H
C
TE
E
104
ÉC
E
U
IQ
Chapitre 2. Cosmologie observationnelle
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
T
Y
L
PO
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
Fig. 2.25: Courbes de vitesse d’iso-récession de la galaxie NGC 5033 déduites du déplacement
Doppler shift de la raie de 21 cm de l’hydrgène atomique [110]. Les courbes sont superposées
à une image optique de la galaxie. L’échelle angulaire de la plus grande dimension est en
minutes d’arc. (Avec la permission de A. Bosma.)
ÉC
E
L
O
E
Exercices sur le chapitre 2
N
H
EC
E
U
IQ
105
2.9 Les indicateurs de distance les plus sûrs jusqu’à ∼ 50 Mpc sont les étoiles variables
Céphéides . La méthode la plus sûre pour étalonner la relation période-luminosité des
Céphéides consiste à utiliser le grand nombre de Céphéides observées dans le grand
nuage de Magellan (LMC). Bien évidemment, cette méthode d’étalonnage demande
de connaître la distance du LMC.
Une des mesures les plus directes de la distance du LMC utilise les binaires à
éclipses. Ces systèmes sont formés de deux étoiles en orbite relative dont le plan
orbital est orienté de telle façon que, vues de la Terre, les deux étoiles s’éclipsent l’une
l’autre. Pour des binaires à éclipses à la distance du LMC, les deux étoiles ont une
séparation angulaire tellement faible que les deux étoiles ne peuvent pas être résolues
optiquement. Elles apparaissent plutôt comme une étoile unique dont la luminosité
est périodique en raison des éclipses périodiques.
La ﬁgure 2.26 montre la courbe de lumière (magnitude apparente en fonction du
temps) du système binaire HV2274 dans le LMC [111]. Deux éclipses apparaissent avec
une période de 5.726 jours. La variation de magnitude de 0.75 pendant les éclipses
correspond à un facteur 2 en ﬂux, ce qui indique qu’il s’agit d’une éclipse totale de
deux étoiles de même luminosité et de même rayon.
Les raies spectrales des deux étoiles ne coïncident pas à cause du déplacement
Doppler dû à leur mouvement orbital. On peut donc déterminer indépendamment la
vitesse de récession de chacune des étoiles. La variation des deux vitesses en fonction
du temps est montrée sur la ﬁgure 2.26.
(a) Estimer la vitesse orbitale des deux étoiles et le rayon de l’orbite (circulaire).
(b) En supposant que les deux étoiles ont même masse, estimer cette masse (en unités
M ).
(c) Utiliser la durée des éclipses pour estimer le rayon commun des deux étoiles (en
unités R ).
(d) La température de surface des deux étoiles est de ∼ 23 000 Kelvin. Le ﬂux mesuré
indique, via (2.1), une taille angulaire de D/R = 9.48 × 10−12 . Estimer la distance R
de HV2274. Après une petite correction pour tenir compte de la distance relative de
HV2274 et du centre du LMC, les auteurs de [111] donnent une distance du LMC de
45.77 ± 1.6 kpc.
(e) La ﬁgure 2.5 montre la magnitude apparente des Céphéides du LMC en fonction
de leur période en fonction de leur période. En utilisant la distance au LMC, transformer ces magnitudes en magnitudes absolues. Comparer ces magnitudes avec celles de
Céphéides de distance déterminée par parallaxe [52], MV = −2.81 log P − 1.43 ± 0.16
(période P en jours). Comparer la valeur de H0 qui serait estimée en utilisant les
Céphéides d’Hipparcos avec celle obtenu à l’aide des Céphéides du LMC.
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
T
Y
L
PO
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
2.10 Il peut paraître surprenant que l’on puisse estimer théoriquement la luminosité
d’une étoile sans connaître les réactions nucléaires qui alimentent cette étoile. Pour
comprendre comment on peut le faire, considérons une sphère de rayon R contenant
Np protons et Np électrons sous forme d’un gaz ionisé idéal.
(a) Si la sphère est de densité uniforme, et si elle est en équilibre hydrostatique avec
ÉC
E
L
O
E
106
ÉC
E
U
IQ
Chapitre 2. Cosmologie observationnelle
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
T
Y
L
PO
N
H
EC
E
U
IQ
Fig. 2.26: Le système binaire HV2274 dans le LMC [111]. Le panneau du haut montre la
U
Q
I
N
vitesse de récession des deux composantes stellaires en fonction de la phase orbitale (période
= 5.726 jours). Le panneau du bas montre la courbe de lumière (magnitude apparente en
fonction du temps).
ÉC
E
L
O
Y
L
PO
H
C
TE
E
Exercices sur le chapitre 2
T
Y
L
PO
N
H
EC
E
U
IQ
107
une pression moyenne P et un volume V , montrer que
E
L
O
3P V = −Eg ∼ (3/5)
Gm2p Np2
,
R
(2.38)
où Eg est l’énergie gravitationnelle totale de la sphère et mp la masse du proton.
Le facteur numérique (3/5) dans (2.38) provient de l’hypothèse que la densité
est uniforme. Cela n’est pas le cas pour une étoile, mais une densité non uniforme
changerait tout simplement ce facteur numérique. Dans les reste de l’exercice, nous
ne nous préoccupons pas des facteurs numériques.
En appliquant la loi des gaz parfaits à (2.38), on peut estimer la température
moyenne T dans l’étoile :
ÉC
T ∼
Gm2p Np
.
R
(2.39)
E
U
IQ
(b) En supposant que la sphère contient des photons en équilibre thermique à la
température T , montrer que le nombre total de photons dans l’étoiles est
Å
ã
mp 6
Nγ ∼ Np3
,
(2.40)
mpl
où mpl = c/G = 1.2 × 1019 GeV est la masse de Planck. Comparer Nγ avec Np
pour le soleil (Np ∼ 1057 ).
Les photons diﬀusent dans l’étoile avant de s’échapper à la surface. Le nombre de
collisions dans cette marche au hasard est de l’ordre de
Å ã2
R
,
(2.41)
Ncol ∼
λ
ÉC
E
L
O
T
Y
L
PO
N
H
EC
où λ est le libre parcours moyen d’un photon dans l’étoile.
(c) Montrer que le temps moyen d’échappement d’un photon est
τ ∼
Np σ
,
Rc
(2.42)
où σ est la section eﬃcace moyenne photon-particule dans l’étoile. À partir de cela,
montrer que la luminosité stellaire est
Å
ã
mp 8 c2
3
.
(2.43)
L ∼ Np
mpl
σ
H
C
TE
U
Q
I
N
Pour une étoile comme le Soleil, les atomes sont presque tous ionisés sauf au voisinage
de la surface. Il s’ensuit que σ ∼ σT (la section eﬃcace Thomson). Pour N = 1057 ,
comparer la luminosité obtenue par (2.43) avec L .
Un traitement plus minutieux des facteurs numériques multiplie le résultat cidessus par π 4 /(5 × 38 ) ∼ 3 × 10−3 [112]. Cela donne un accord tout à fait acceptable
avec la luminosité solaire observée étant donné les approximations faites dans ce calcul.
ÉC
E
L
O
Y
L
PO
E
108
E
U
IQ
Chapitre 2. Cosmologie observationnelle
T
Y
L
PO
N
H
EC
On note que (2.43) prévoit qu’une luminosité stellaire est proportionnelle au cube
de la masse, ce qui est en bon accord avec l’observation.
Si la luminosité d’une étoile ne dépend que de sa masse, on peut se demander quel
est le rôle des réactions nucléaires qui alimentent l’étoile. La réponse est qu’elles permettent à l’étoile de brûler plus longtemps avec un rayon stable. Une étoile commence
sa vie sous forme d’un nuage diﬀus trop froid pour que les réactions nucléaires s’allument. Ce nuage rayonne néanmoins des photons en raison de (2.43). En rayonnant
de l’énergie, la conservation de l’énergie implique que le rayon de l’étoile diminue.
Lorsque l’étoile devient plus petite, sa température augmente jusqu’à ce que les réactions nucléaires s’allument. À ce moment-là, une régime stable est atteint où l’énergie
rayonnée est compensée par l’énergie libérée par les réactions nucléaires.
ÉC
E
L
O
E
U
IQ
2.11 À peu près 10% de la masse des grands amas de galaxies se trouve dans du
gaz intergalactique ionisé en équilibre hydrostatique. Ce gaz produit des photons par
bremsstrahlung :
N
H
EC
e− p → e− p γ .
T
Y
L
PO
(2.44)
Les spectres théorique et expérimental sont représentés sur les ﬁgures 2.27 et 2.28.
Contrairement aux photons produits dans les étoiles, ces photons s’échappent directement de l’amas :
(a) Le plus grand amas contient ∼ 1014 M d’hydrogène ionisé dans un rayon de
∼ 1 Mpc. Veriﬁer que le libre parcours moyen des photons dû à la diﬀusion Thomson
dans l’amas est plus grand que le rayon de l’amas.
(b) La section eﬃcace Rutherford à grand angle est ∼ σT /(v/c)4 . Veriﬁer que le libre
parcours moyen eﬀectif des électrons (qui diﬀusent sur des protons) dans l’amas est
plus faible que le rayon de l’amas. Cela justiﬁe l’hypothèse que les électrons et les
protons forment un gaz thermique en équilibre hydrostatique.
Pour des électrons non-relativistes, la section eﬃcace diﬀérentielle de production
de photons d’énergie Eγ par bremsstrahlung est approximativement [113]
ÉC
E
L
O
dσ
c2 σT
∼ α 2
dEγ
v Eγ
Eγ (1/2)me v 2 ,
(2.45)
U
Q
I
N
où α ∼ 1/137 est la constante de structure ﬁne, v c est la vitesse relative électron–
proton, et σT la section eﬃcace Thomson.
En faisant un raisonnement qui sera justiﬁé au chapitre 6, on sait que le taux de
production par unité de volume des photons est proportionnel à la section eﬃcace
diﬀérentielle (2.45), à la densité électronique ne , à la densité de protons np ∼ ne , et
à la vitesse moyenne électron–proton :
ÉC
E
L
O
Y
L
PO
H
C
TE
dNγ
dσ
c
σT
∼ n2p v
∼ n2p αc
.
dtdV
dEγ
v
Eγ
(2.46)
E
Exercices sur le chapitre 2
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
T
Y
L
PO
E
U
IQ
N
H
EC
109
E
U
IQ
Fig. 2.27: Spectre théorique des rayons X d’un amas galactique à une température de 7 keV.
Le spectre suit la section eﬃcace de bremsstrahlung en 1/E à basse énergiee et il décroît
exponentiellement aux énergies supérieures à la températue. Des raies de recombinaison du
fer apparaissent vers 6 keV. La deuxième courbe qui a un ﬂux atténué à basse énergie montre
l’eﬀet de l’absorption dans la Voie Lactée. Avec la permission de Monique Arnaud.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
110
ÉC
E
U
IQ
Chapitre 2. Cosmologie observationnelle
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
T
Y
L
PO
N
H
EC
E
U
IQ
Fig. 2.28: Spectre en rayons X émis par l’amas de galaxies Abell 1413 observé par le
satellite ACSA. La structure du spectre autour de 2 keV provient de la variation d’eﬃcacité
du système de détection. La température de l’amas, obtenue par ajustement, est de 7.6 Kelvin.
Avec la permission de Monique Arnaud.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Exercices sur le chapitre 2
T
Y
L
PO
N
H
EC
E
U
IQ
111
(c) Integrer cette expression jusqu’à un cutoﬀ dans l’énergie des photons donné par la
température T de l’amas pour trouver la luminosité totale en rayons X (énergie/unité
de temps) :
Lx ∼ n2p αcσT me c2 T D3 ,
(2.47)
ÉC
E
L
O
où D est le diamètre de l’amas.
(d) Montrer que le nombre total de baryons, Nb , dans l’amas peut être estimé à partir
du ﬂux de rayons X φx observé :
Nb2 ∼
φx R5 θ3
√
,
αcσT me c2 T
(2.48)
où θ est le diamètre angulaire observé de l’amas et R sa distance. Cette formule montre
que si le redshift d’un amas est utilisé pour estimer sa distance, la masse baryonique
−5/2
totale de l’amas se comporte comme h70 .
(e) Modiﬁer (2.38) de façon que la pression thermique ne supporte que la masse
baryonique de l’amas, et montrer ainsi que la masse totale de l’amas s’exprime en
fonction de sa température T en rayons X par
E
L
O
où r est le rayon de l’amas.
ÉC
ÉC
T
Y
L
PO
Mtot ∼
E
L
O
6kT r
Gmp
N
H
EC
Y
L
PO
E
U
IQ
(2.49)
H
C
TE
U
Q
I
N
E
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
ÉC
N
H
EC
T
Y
L
PO
E
L
O
E
U
IQ
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
E
T
Y
L
PO
N
H
EC
E
U
IQ
E
L
3
CO
ÉChapitre
Coordonnées et métriques
E
U
IQ
Aﬁn d’étudier le mouvement des galaxies et des photons, nous allons avoir besoin d’un système de coordonnées et de sa métrique. De façon générale, un système
de coordonnées attribue à tout événement une coordonnée temporelle, x0 , et trois
coordonnées spatiales, xi , i = 1, 2, 3. Le tenseur métrique gµν donne le carré du
temps propre dτ , c’est-à-dire le temps eﬀectivement mesuré par une horloge lorsque
ses coordonnées d’espace changent de dx1 , dx2 , dx3 pendant une variation dx0 de sa
coordonnée temporelle :
ÉC
E
L
O
T
Y
L
PO
dτ 2 =
3
N
H
EC
gµν dxµ dxν ,
(3.1)
µ,ν=0
où, sans perte de généralité, on peut prendre gµν = gνµ . L’utilité de la métrique vient
du fait qu’en l’absence de forces non-gravitationnelles, des particules test massives
suivent des trajectoires qui maximisent leur temps propre écoulé et que les particules
de masse nulle suivent des trajectoires de temps propre nul. La connaissance de la
métrique permet de calculer les trajectoires des galaxies et des photons.
Dans tout ce livre, nous utiliserons seulement la relativité « sans double décimètre » où les distances sont mesurées par des temps de vol de photons. Un système
de coordonnées simple peut être construit en équipant un observateur à la dérive
(en chute libre) dans l’espace intergalactique d’une horloge et d’un émetteur radar.
Comme l’illustre la ﬁgure 3.1, l’observateur peut mesurer le temps et la distance
d’un événement de la façon habituelle. Le photon est émis au temps ta (mesuré par
l’horloge), il est réﬂéchi par l’événement en question, puis détecté par l’observateur à
l’instant tb (mesuré par l’horloge). On peut attribuer à l’événement une coordonnée
de temps T et une coordonnée radiale R
tb + t a
T =
2
ÉC
E
L
O
Y
L
PO
R =
H
C
TE
tb − t a
.
2
U
Q
I
N
(3.2)
Nous verrons que si l’événement n’est pas trop éloigné de l’observateur, cette procé113
E
114
ÉC
E
U
IQ
Chapitre 3. Coordonnées et métriques
E
L
O
T
Y
L
PO
N
H
EC
T
tb
T
Y
L
PO
(T,R)
ÉC
E
L
O
N
H
EC
E
U
IQ
ta
R
Fig. 3.1: Construction d’un système de coordonnées par un observateur équipé d’une horloge
et d’un radar. L’observateur émet un photon à t = ta et ce photon est réﬂéchi par l’événement
en question. Le photon revient chez l’observateur à t = tb . L’observateur peut attribuer à
l’événement réﬂexion la coordonnée radiale R = (tb − ta )/2 et la coordonnée temporelle
T = (tb + ta )/2. Il se trouve que si l’observateur est en chute libre, la métrique du système
(T, R) est localement lorentzienne à l’origine. Malheureusement, ce système de coordonnées
ne peut être utilisé pour couvrir tout l’univers à cause de l’existence d’horizons.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
T
Y
L
PO
N
H
EC
E
U
IQ
115
dure pour déﬁnir des coordonnées donne la formule habituelle pour le temps propre
dτ 2 = dT 2 − dX 2 − dY 2 − dZ 2 ,
E
L
O
(3.3)
où X = R sin θ cos φ, Y = R sin θ sin φ, Z = R cos θ où θ et φ sont les coordonnées
sphériques angulaires habituelles de l’événement vues par l’observateur. En termes de
métrique, cela signiﬁe
ÉC
g11 = g22 = g33 = = −1
g00 = 1
gµ=ν = 0 .
(3.4)
Bien que ce système de coordonnées soit très commode pour les événements
proches, il ne peut pas être utilisé, même en principe, pour décrire les événements
cosmologiques les plus lointains. La raison en est que les photons que nous recevons
maintenant d’objets de grand redshift on été émis avant que ces objets aient pu recevoir des photons de notre part. Autrement dit, nous étions au delà de l’horizon de
ces objets au moment de l’émission. À cause de ce problème d’horizon, nous avons
besoin, au minimum, d’un réseau d’horloges distribué dans tout l’univers.
Il se trouve que le système de coordonnées le plus pratique pour la cosmologie est
un système de coordonnées « comobiles ». De tels systèmes mesurent les coordonnées
temporelles avec des horloges « comobiles », c’est-à-dire des horloges qui participent à
l’expansion universelle. Un événement dans une galaxie se voit donc attribuer une coordonnée temporelle mesurée par une horloge de cette même galaxie. De plus, comme
nous l’illustrons sur la ﬁgure 3.2, dans des systèmes comobiles, les galaxies se voient
attribuer des coordonnées spatiales qui sont indépendantes du temps. Les coordonnées comobiles sont par conséquent très diﬀérentes des traditionnelles coordonnées
« du laboratoire » dans lesquelles les galaxies en récession ont des coordonnées spatiales qui dépendent du temps alors que la coordonnée temporelle est mesurée par des
horloges ﬁxes par rapport à l’origine.
Nous allons commencer ce chapitre dans la section 1 en discutant de façon plus
détaillée comment la gravitation se décrit de façon relativiste. Nous mettrons l’accent
sur le fait que, dans la relativité restreinte comme en relativité générale, les particules
libres massives suivent des trajectoires qui maximisent leur temps propre. De telles
trajectoires sont appelées des « géodésiques ». La diﬀérence première entre la relativité restreinte et la relativité générale est que, dans la seconde, la métrique n’est
pas constante, c’est une fonction de la position qui permet de décrire les eﬀets de la
gravitation.
Dans la section 2 nous entreprendrons le véritable travail de ce chapitre en donnant des déﬁnitions opératoires pour les coordonnées comobiles. La métrique de ce
système sera alors écrite dans les deux sections suivantes. Comme nous le verrons,
certaines caratéristiques de la métrique sont de pures conséquences de la déﬁnition
des coordonnées, alors que d’autres sont liées aux hypothèses que nous faisons sur les
caractéristiques de l’espace-temps. La première hypothèse, utilisée dans la section 3,
sera de supposer l’univers comme isotrope autour de l’origine, c’est-à-dire qu’il n’y
a pas de direction privilégiée. La seconde, utilisée dans la section 4, sera que l’univers est homogène, c’est-à-dire qu’il n’y a pas d’origine spatiale privilégiée. Ces deux
hypothèses nous mèneront à la métrique de Robertson-Walker.
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
E
116
E
U
IQ
Chapitre 3. Coordonnées et métriques
T
Y
L
PO
N
H
EC
Après avoir déﬁni cette métrique, nous traiterons le problème des trajectoires de
particules en coordonnées comobiles. Dans la section 5, nous considérerons la classe
de trajectoires la plus importante : celle de photons voyageant entre des galaxies
distantes et notre position à l’origine. Ce traitement nous permettra d’établir, à la
section 6, les relations cosmologiques entre les luminosités et les ﬂux mesurés, ainsi
qu’entre la taille des objets et les distances angulaires mesurées.
Dans la section 7, nous traiterons le problème général du mouvement des particules
en déduisant l’équation des géodésiques. Nous calculerons l’équation des géodésiques
dans la métrique de Robertson-Walker, ce qui permettra de traiter le mouvement de
particules-test dans un univers homogène.
Finalement, dans la section 8 nous trouverons l’équation des géodésiques pour un
champ gravitationnel à symétrie sphérique. Cela nous permettra de traiter le problème, important pour la cosmologie, de l’eﬀet de lentille gravitationnelle des amas
de galaxies.
ÉC
1
E
L
O
Relativité et gravitation
T
Y
L
PO
N
H
EC
E
U
IQ
Traditionnellement, on déduit les lois de la relativité restreinte à partir de deux
postulats :
– Il existe une inﬁnité de systèmes de coordonnées, en mouvement relatif uniforme,
dans lesquels les lois de la physique peuvent être exprimées sous la même forme.
Ces systèmes sont dits des référentiels « d’inertie » ou « galiléens ».
ÉC
E
L
O
– La vitesse de la lumière est la même dans tous les référentiels d’inertie.
En dépit de l’importance historique du postulat sur la vitesse de la lumière, si
l’on veut comprendre la relation entre relativité restreinte et relativité générale, il est
préférable de le remplacer par un postulat aussi puissant :
– Une horloge se déplaçant à la vitesse v dans un référentiel d’inertie aﬃchera un
intervalle de temps dτ , entre deux événements sur sa trajectoire, plus petit que
l’intervalle de temps dt mesuré par un système d’horloges au repos :
»
(3.5)
dτ = dt 1 − v 2 /c2 .
U
Q
I
N
Le temps τ est appelé le « temps propre » de l’horloge de vitesse v 1 .
H
C
TE
La conﬁrmation expérimentale du postulat (3.5) est plus frappante que celle du postulat sur la vitesse de la lumière. Les expériences menées sur les accélérateurs de
particules de haute énergie montrent sans conteste que la durée de vie moyenne d’une
particule instable est proportionnelle à γ = (1 − v 2 /c2 )−1/2 . Voyons comment ce fait
empirique est relié à (3.5). Considérons un observateur imaginaire qui se déplace avec
E
L
O
Y
L
PO
1 Comme pour le postulat sur la vitesse de la lumière, ce postulat demande un certain soin dans
la déﬁnition de la procédure expérimentale qu’on utilise pour le vériﬁer. En particulier, les horloges
au repos doivent être synchronisées. Voir l’exercice 3.12.
ÉC
E
Relativité et gravitation
ÉC
E
L
O
T
Y
L
PO
N
H
EC
t1
R2
R2
R1
R1
θ
θ
T
Y
L
PO
χ
E
L
O
χ
ÉC
2
χ
117
t 2 > t1
lab coordinates:
comoving coordinates:
E
U
IQ
2
χ
N
H
EC
E
U
IQ
1
1
θ
θ
Fig. 3.2: Mouvement d’une galaxie de vitesse particulière négligeable dans des coordonnées
du laboratoire et dans des coordonnées comobiles. Dans les coordonnées du laboratoire, la
coordonnée radiale R évolue dans le temps selon la loi de Hubble. Dans les coordonnées
comobiles, la coordonnée radiale χ est indépendante du temps. Dans les deux systèmes, les
coordonnées angulaires de la galaxie sont indépendantes du temps.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
118
E
U
IQ
Chapitre 3. Coordonnées et métriques
T
Y
L
PO
N
H
EC
les particules. L’observateur peut utiliser la loi de désintégration exponentielle des
particules comme horloge en suivant l’évolution du nombre Nv de particules de même
vitesse v que lui-même. Avec cette horloge, l’observateur mesure son (propre) temps
propre par la relation
ÉC
E
L
O
dτ = −T
dNv
,
Nv
(3.6)
où T est la durée de vie moyenne des particules dans leur référentiel au repos, (qui
est le référentiel de l’observateur). Le temps t dans le référentiel du laboratoire peut
être mesuré de la même façon avec un ensemble de N0 particules de vitesse v = 0 :
dt = −T
dN0
,
N0
(3.7)
qui, combiné avec (3.6), donne
N
H
EC
dτ
dNv /Nv
=
.
dt
dN0 /N0
T
Y
L
PO
E
U
IQ
(3.8)
Expérimentalement, on observe que les particules en mouvement se désintègrent plus
lentement que les particules au repos :
ÉC
E
L
O
»
dNv /Nv
=
1 − v 2 /c2 .
dN0 /N0
(3.9)
En combinant ce résultat expérimental avec la déﬁnition de dτ (3.6) et dt (3.7) on
conﬁrme (3.5).
Comme on le montre dans l’exercice 3.12, les transformations de Lorentz peuvent
être déduites de (3.5).
Une manifestation de (3.5) est le fameux paradoxe des jumeaux de Langevin.
Considérons deux horloges initialement au même point (t1 , r1 ). Une des horloges reste
en r1 (considéré comme un référentiel d’inertie) alors que l’autre horloge suit une
trajectoire de vitesse non uniforme v(t) avant de venir retrouver son horloge jumelle
à (t2 , r1 ). Pendant son voyage, l’horloge de vitesse non uniforme compte un temps2
t2
dτ =
t1
»
t2
dt
1−
v(t)2 /c2
t1
E
L
O
dt .
t1
La jumelle avec v = 0 compte un temps
t2
dτ =
t1
t2
<
Y
L
PO
t2
dt .
H
C
TE
U
Q
I
N
(3.10)
(3.11)
t1
2 Il a été vérifé expérimentalement que (3.5) s’applique aux horloges de vitesse non uniforme,
notamment en étudiant la durée de vie de particules instables maintenues en orbite dans des anneaux
de stockage [114].
ÉC
E
Relativité et gravitation
T
Y
L
PO
N
H
EC
E
U
IQ
119
On voit que l’horloge stationnaire compte nécessairement un temps plus long que sa
jumelle. Puisque l’horloge en mouvement a été obligée d’accélérer puis de décélérer
pour revenir à son point de départ, le paradoxe des jumeaux nous permet de déduire
un principe fondamental qui régit le mouvement des particules :
E
L
O
– En l’absence de forces, une particule massive suit un chemin dans l’espace-temps
qui maximise son temps propre par rapport à tous les chemins voisins qui ont
les mêmes points de départ et d’arrivée. Les chemins qui maximisent le temps
propre sont appelés des « géodésiques » de l’espace-temps.
ÉC
Alors que nous avons abouti à cette conclusion en comparant une horloge stationnaire avec une horloge en mouvement, elle est complètement générale car on peut
toujours choisir un référentiel où l’horloge qui n’est pas accélérée est au repos.
Quelques exemples de géodésiques sont montrés sur la ﬁgure 3.3.
Pour nous préparer à plonger dans la relativité générale, il est utile de trouver une
expression plus générale pour le temps propre. L’équation (3.5) montre que dans un
référentiel d’inertie, le temps propre est donné par
N
H
EC
E
U
IQ
dτ 2 = dt2 − dr2 = dx0 dx0 − (dx1 dx1 + dx2 dx2 + dx3 dx3 ) ,
T
Y
L
PO
(3.12)
où x0 = t et (x1 , x2 , x3 ) = r. Cette équation est équivalente à3
E
L
O
dτ 2 =
ÉC
3
ηµν dxµ dxν ≡ ηµν dxµ dxν ,
(3.13)
µ,ν=0
où la métrique ηµν est
η00 = 1
η11 = η22 = η33 = −1
ηµ=ν = 0 .
(3.14)
Nous appellerons des coordonnées qui satisfont (3.13) des « coordonnées Lorentziennes ». Un espace-temps où il est possible de trouver un système de coordonnées
Lorentziennes est dit être « plat ». Notons qu’un système de coordonnées Lorentziennes peut être transformé en un autre système de coordonnées Lorentziennes par
des rotations d’espace, ou par des « boosts » de Lorentz (exercice 3.1). Cela signiﬁe
que les observateurs qui utilisent tous de telles coordonnées observent la même loi
(3.5).
En présence d’une force gravitationnelle (et d’aucune autre force), les particules
suivent toujours des trajectoires qui maximisent leur temps propre pour la simple
raison que la force gravitationnelle peut être éliminée dans une petite région de l’espace
en utilisant un système de coordonnées en « chute libre ». Le principe d’équivalence
qui pose que les masses gravitationnelle et inertielle sont égales, garantit que toutes
les particules sont accélérées de la même façon. Par conséquent, on peut éliminer
l’accélération en utilisant des coordonnées en chute libre. C’est cela qui provoque
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
3 Les indices répétés comme µ et ν dans (3.13) impliquent une sommation (sur ces indices) et nous
.
adoptons la convention d’Einstein d’omettre le signe
ÉC
E
120
ÉC
E
U
IQ
Chapitre 3. Coordonnées et métriques
E
L
O
T
Y
L
PO
N
H
EC
t
b1
b0
b2
a1
a0
T
Y
L
PO
c1
ÉC
E
L
O
N
H
EC
E
U
IQ
c0
c2
x
Fig. 3.3: Trois géodésiques, a0, b0, et c0, dans un espace-temps (plat) à deux dimensions
(x, t). Le chemin avec v = 0, a0, maximise manifestement le temps propre (3.5) puique son
voisin a1 a une vitesse non-nulle sur tout le chemin. Le chemin b0 maximise également le
temps propre comme on le constate en le ragardant dans un référentiel où sa vitesse est nulle,
ou en utilisant l’équation de la géodésique (exercice 3.2). Le chemin c0 est une géodésique
de longueur nulle, ∆τ = 0, ce qui correspond à la trajectoire d’une d’une particule de masse
nulle. Tous ses voisins, comme c1 et c2, sont non-physiques puisqu’ils ont ∆τ 2 < 0 sur un
certain intervalle (les segments de pente inférieure à un).
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Relativité et gravitation
T
Y
L
PO
N
H
EC
E
U
IQ
121
l’état d’apesanteur ressenti par les astronautes. Une collection de particules dans une
région de l’espace inﬁniment petite, apparaît comme obéissant aux lois de la relativité
restreinte. En eﬀet, les référentiels en chute libre constituent, localement, les meilleurs
exemples de référentiels d’inertie. Il en découle que, dans une région inﬁnitésimale,
on peut choisir des coordonnées en chute libre, x̃µ , µ = 0, 1, 2, 3, centrées sur cette
région, de telle façon que la métrique soit
ÉC
E
L
O
gµν (x̃ = 0) = ηµν .
(3.15)
Dans cette région, les particules suivent les géodésiques de la relativité restreinte,
c’est-à-dire des lignes droites.
Alors que la force gravitationnelle peut être éliminée dans une petite région de
l’espace, des particules largement séparées dans un champ gravitationnel non uniforme
vont subir des accélérations relatives. Par exemple, dans le champ gravitationnel de
la Terre, une particule sera accélérée vers le centre de la Terre. Par conséquent, deux
particules séparées horizontalement et lâchées seront vues, par un observateur en chute
libre avec elles, comme étant accélérées l’une vers l’autre (Fig. 3.4). Nous verrons dans
la section 6 que ces eﬀets de marée peuvent être pris en compte dans une métrique
qui a des corrections du second ordre par rapport à la métrique de Lorentz
T
Y
L
PO
gµν (x̃) = ηµν + O(x̃2 )
N
H
EC
E
U
IQ
(coordonnées en chute libre) .
(3.16)
Les coeﬃcients des termes quadratiques dans la métrique seront contraints par la
densité locale d’énergie et d’impulsion au travers des équations des champs d’Einstein
qui seront vues au chapitre 4.
Nous n’aurons pas toujours à utiliser des coordonnées en chute libre, par conséquent il nous faut utiliser des métriques plus générales. Par exemple, il est souvent
utile d’utiliser un système ﬁxe dans un champ gravitationnel. Les expériences avec
des horloges atomiques embarquées et la mesure de la déﬂexion des photons dans des
champs gravitationnels indiquent que le temps propre est donné par
ÉC
E
L
O
dτ 2 ∼ dt2 [1 + 2Φ(r)] − [1 − 2Φ(r)]dr2 ,
(3.17)
c’est-à-dire
g00 ∼ 1 + 2Φ
g11 = g22 = g33 ∼ −1 + 2Φ
gµ=ν ∼ 0 ,
2
(3.18)
où Φ(r) est le potentiel gravitationnel (divisé par c ; dans la suite nous omettrons les
facteurs c) à la position de l’horloge. Nous verrons au chapitre 4 (exercice 4.8) que
(3.17) est la solution des équations d’Einstein pour un champ gravitationnel faible,
Φ 1. Avec cette métrique, le paradoxe des jumeaux peut être considéré dans l’autre
sens. L’horloge qui quitte la Terre et revient, compte un intervalle de temps supérieur
à celui compté par l’horloge restée à l’origine (exercice 3.3).
Le choix de la métrique (3.18) sera conﬁrmé lorsque les techniques de la section 7
nous permettront de montrer que les géodésiques satisfont l’équation
ÉC
E
L
O
Y
L
PO
d2r
Φ(r) ,
= −∇
dt2
H
C
TE
U
Q
I
N
(3.19)
E
122
ÉC
E
U
IQ
Chapitre 3. Coordonnées et métriques
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
T
Y
L
PO
N
H
EC
E
U
IQ
H
C
TE
U
Q
I
N
Fig. 3.4: Quatre particules séparées par de petites distances dans le champ gravitationnel de
Y
L
PO
la Terre. Toutes les particules tombent vers le centre de la Terre en suivant des chemins qui
maximisent leur temps propre individuel par comparaison avec des chemins voisins (exercice
3.4). Comme les chemins ne sont pas parfaitement parallèles, un observateur en chute libre
verra que les particules ont de petites accélérations relatives dues à des eﬀets de marée, c’està-dire à la non-uniformité du champ gravitationnel. Les deux particules à la même distance
radiale apparaîtront comme étant accélérées l’une vers l’autre. Deux particules à des distance
diﬀérentes apparaîtront comme étant accélérées en sens inverse. Dans la relativité générale,
ces accélérations relatives sont régies par le tenseur de Riemann (Chapitre 4, sect. 6).
ÉC
E
L
O
E
Coordonnées comobiles
T
Y
L
PO
N
H
EC
E
U
IQ
123
c’est-à-dire l’équation de Newton habituelle.
Dans un univers homogène, le concept de potentiel gravitationnel n’est pas très
utile et la métrique (3.18) ne peut pas être utilisée. Nous allons donc recommencer
dans la section suivante en déﬁnissant un système de coordonnées comobile utile en
cosmologie. La métrique pour un système de ce genre se trouvera être paramétrisée
par le paramètre d’échelle a(t) et un paramètre de courbure spatiale k. Ces deux
paramètres seront déterminés au chapitre 4 à partir de la densité d’énergie-impulsion
avec les équations d’Einstein.
ÉC
2
E
L
O
Coordonnées comobiles
Dans cette section, nous allons trouver un système de coordonnées comobile utile
pour un univers en expansion. Pour un événement qui se produit près d’une galaxie (ou
un observateur imaginaire en récession selon la loi de Hubble) nous avons besoin d’une
coordonnée temporelle t, de deux coordonnées angulaires, (θ, φ), et d’une coordonnée
radiale χ.
N
H
EC
E
U
IQ
– Comme origine spatiale, nous choisissons (bien entendu) notre propre position.
– Comme coordonnée de temps, nous allons utiliser le temps mesuré par une
horloge attachée à la galaxie (ou l’observateur) en récession. Une telle horloge
est appelée horloge « comobile » :
ÉC
E
L
O
T
Y
L
PO
t = temps mesuré par des horloges comobiles .
(3.20)
Les horloges peuvent être synchronisées au moment du « big bang » ou à
n’importe quel événement bien déﬁni (recombinaison, nucléosynthèse).
– Comme coordonnées angulaires, nous prenons les angles polaire et azimuthal
habituels des événements vus par rapport à une direction arbitrairement choisie
θ, φ = angles vus sur la voûte céleste .
(3.21)
– La déﬁnition de la coordonnée radiale va demander de déﬁnir la « distance
spatiale ». La distance spatiale dS entre des horloges comobile voisines est
déﬁnie par
dS (dχ, dθ, dφ) ≡ temps de vol d un photon sur (dχ, dθ, dφ) .
(3.22)
U
Q
I
N
Par « voisines » nous entendons qu’elles sont suﬃsamment proches l’une de
l’autre pour qu’on puisse négliger l’expansion universelle pendant le voyage des
photons. Notons que nous pouvons mesurer des distances par des temps de vol
« aller simple » car nos horloges comobiles ont été synchronisées.
– Comme coordonnée radiale sans dimension, χ, nous choisissons de prendre la
« distance » R de l’origine divisée par le paramètre d’échelle. Pour des distances
inﬁnitésimales, on a :
ÉC
E
L
O
dχ ≡
Y
L
PO
H
C
TE
1
dR
=
[ dS]dθ=dφ=0 .
a(t)
a(t)
(3.23)
E
124
ÉC
E
U
IQ
Chapitre 3. Coordonnées et métriques
T
Y
L
PO
N
H
EC
– La distance entre des observateurs comobiles qui ne sont pas « voisins » est plus
diﬃcile à déterminer car les distances changent avec le temps. Pour mesurer la
distance suﬃsamment rapidement aﬁn qu’elle ne change pas pendant la mesure,
nous utilisons un réseau d’horloges comobiles synchrones et des émetteurs de
photons, comme on l’a illustré sur la ﬁgure 3.5. Cette ﬁgure montre comment
mesurer la distance, au temps t, entre l’origine et une galaxie lointaine. Au
temps prédéterminé t, chaque station i envoie un photon à la station suivante
et compte le temps ∆ti qu’il faut pour qu’arrive le photon emis par la station
précédente. La distance intégrée est la somme des temps de vol :
∆ti .
(3.24)
S(t) =
dS =
E
L
O
i
Il doit être clair pour le lecteur que, pour le moment, χ est une coordonnée de
pensée (gedanken). Plus loin, nous verrons comment χ peut être déterminé par
des mesures de redshift.
N
H
EC
E
U
IQ
Avant de calculer la métrique pour notre système de coordonnées, il faut mettre
l’accent sur quelques points. D’abord, l’utilisation des coordonnées comobiles est avant
tout une question de commodité pratique puisque, comme nous le verrons, le mouvement des photons et des galaxies est simple dans de telles coordonnées. Cela provient
en partie de ce que, dans la limite de vitesses particulières négligeables, les galaxies ont
des coordonnées spatiales (χ , θ , φ) indépendantes du temps. Encore plus important
est le fait que la coordonnée de temps t peut être directement reliée à des processus
physiques se produisant dans les galaxies. L’utilisation d’horloges ﬁxes par rapport
à l’origine imposerait d’utiliser, entre autres choses, un facteur γ pour relier la coordonnée temporelle aux taux de réaction dans les galaxies, par exemple.
Une deuxième raison pour utiliser des coordonnées comobiles est que l’homogénéité de l’univers peut être rendue manifeste dans des coordonnées comobiles où
toutes les galaxies sont traitées de façon équivalente (mis à part le choix de l’origine
spatiale) Cette propriété sera exploitée dans les deux sections suivantes lorsque nous
déterminerons la métrique.
D’un autre côté, il faut souligner que des coordonnées comobiles ne sont pas des coordonnées d’un référentiel d’inertie (même localement) et certains résultats, bien que
simple mathématiquement, ne seront pas intuitifs. S’agissant d’eﬀets locaux, comme
la propagation de photons entre observateurs voisins, notre intuition est mieux servie
par des coordonnées en chute libre. Par exemple, la dépendance en temps de la température du CBR a été calculée de cette façon dans la section 2.4. Comme nous le
verrons dans le chapitre 4, les équations d’Einstein pour l’évolution de a(t) sont bien
plus simple si l’on adopte des coordonnées en chute libre.
Enﬁn, soulignons que nos déﬁnitions (3.20), (3.21) et (3.23), des coordonnées comobiles sont ambiguës si la distribution de matière est inhomogène. De la matière
localement condensée peut agir comme une lentille gravitationnelle et un objet donné
peut avoir plus d’une image dans le ciel. Notre déﬁnition des coordonnées angulaires
(θ, φ) est donc ambiguë s’il y a deux images de brillance comparable. La déﬁnition
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Coordonnées comobiles
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
125
(χ , t)
3
(χ , t)
2
N
H
EC
(χ 1 , t)
T
Y
L
PO
(χ =0 , t)
ÉC
E
L
O
E
U
IQ
Fig. 3.5: Par convention, les distances sont mesurées par des réseaux d’horloges synchronisées comobiles et des émetteurs de photons. Ici, nous illustrons la mesure de la distance R3 (t)
entre l’origine et la galaxie 3 à χ3 . Au temps t, les trois émetteurs de photons en χ = 0, χ1 , χ2
émettent un photon vers leur voisin. Les photons sont détectés à (t + ∆t1 , χ1 ), à (t + ∆t2 , χ2 )
et à (t + ∆t3 , χ3 ). Par convention, la distance R3 (t) est R3 (t) = ∆t1 + ∆t2 + ∆t3 .
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
126
E
U
IQ
Chapitre 3. Coordonnées et métriques
T
Y
L
PO
N
H
EC
de χ est également ambiguë puisque plus d’un chemin peut être utilisé pour déterminer la distance à l’origine. L’utilisation d’horloges comobiles attachées aux galaxies
est ambiguë puisque les puits de potentiel d’une galaxie peuvent désynchroniser des
horloges en diﬀérents endroits de la galaxie. Nous n’allons pas tenir compte de ces
eﬀets car, dans l’état actuel de l’univers, ils sont d’importance secondaire si l’on ne
considère que les phénomènes à grande échelle.
É C3
E
L
O
La métrique I : surtout l’isotropie
Dans cette section, nous allons commencer notre recherche d’une métrique appropriée à un univers homogène et isotrope.
La plus grosse part de la métrique est une conséquence de la déﬁnition même des
coordonnées. La coordonnée t est mesurée par des horloges de coordonnées spatiales
constantes ce qui implique
dτ = dt
HN
(dχ = dθ = dφ = 0) .
C
E
T
LY
E
U
IQ
(3.25)
Les distances spatiales inﬁnitésimales dS sont mesurées par des temps de vol de
photons, par conséquent des chemins avec dt = dS(dχ, dθ, dφ) doivent avoir dτ = 0.
Cela suggère
O
P
E
L
ÉCO
dτ 2 = dt2 − dS 2 .
(3.26)
Il s’ensuit que des particules qui se déplacent à des vitesses inférieures à la vitesse de
la lumière (trajectoires avec dt > dS) voient un déﬁlement du temps dτ > 0.
Pour déﬁnir la métrique (3.26) il nous faut dS(dχ, dθ, dφ). La situation est illustrée
sur la ﬁgure 3.6.
La déﬁnition (3.23) de la coordonnée radiale χ implique
dS 2 = a2 dχ2
(dθ = dφ = 0) .
(3.27)
Les distances orthogonales à la direction radiale sont plus délicates à traiter. Considérons deux horloges comobiles à la même coordonnée radiale χ mais séparées (sur
le ciel) de (dθ, dφ). Nous supposons que le temps de vol des photons entre les deux
horloges est proportionnel à leur séparation angulaire observée, qui, en coordonnées
sphériques, est ∆Θ = (dθ2 + sin2 θdφ2 )1/2 . Utiliser le théorème de Pythagore pour
combiner dθ et dφ signiﬁe que l’image des la position des horloges dans le ciel n’est
pas étirée dans une direction quelconque (Fig. 3.6). Cela devrait être le cas dans un
univers isotrope puisque qu’il n’existe pas de direction privilégiée. On s’attend aussi à
ce que le temps de vol soit proportionnel au paramètre d’échelle a(t). Le temps de vol
dépendra également de χ d’une façon que nous allons décrire par une fonction r(χ).
En mettant tous ces facteurs ensemble, nous obtenons
ÉC
E
L
O
Y
L
PO
dS 2 = [a(t)r(χ)]2 (dθ2 + sin2 θdφ2 )
H
C
TE
(dχ = 0) .
U
Q
I
N
(3.28)
E
La métrique I : surtout l’isotropie
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
127
a dχ
(χ,θ,φ)
E
U
IQ
ar sinθ dφ
θ
E
L
O
χ=0
ÉC
aχ
T
Y
L
PO
N
H
EC
ar dθ
φ
U
Q
I
N
Fig. 3.6: Un petit cube de dimension dS à la position (χ, θ, φ). Si l’univers est isotrope par
rapport à l’origine, l’image du cube vue sur le ciel depuis l’origine n’est pas déformée car il n’y
a pas de direction privilégiée le long de laquelle l’image peut être étirée. Le cube de la ﬁgure
apparaîtra donc comme un carré dans le ciel de taille angulaire dθ = sin θdφ = dS/ar. Si, en
plus d’être isotrope, l’univers est « euclidien », la taille angulaire du cube sera inversement
proportionnelle à sa distance à l’origine, c’est-à-dire à r(χ) = χ. Si l’univers est homogène
mais pas nécessairement euclidien, la fonction r(χ) ne dépend pas du choix de l’origine.
ÉC
E
L
O
Y
L
PO
H
C
TE
E
128
E
U
IQ
Chapitre 3. Coordonnées et métriques
T
Y
L
PO
N
H
EC
Le facteur de proportionnalité entre le temps de vol et la séparation angulaire ne
dépend pas de (θ, φ) car nous avons supposé que l’univers est isotrope autour de
l’origine.
Si l’espace est « plat », les durées de vol des photons seront proportionnelles à la
distance à l’origine comme en géométrie euclidienne :
ÉC
E
L
O
r(χ) = χ
(espace plat) .
(3.29)
Un espace qui est « localement plat » n’a que des corrections quadratiques à la
relation euclidienne :
ï
ò
b
r(χ) = χ 1 − χ2 + .....
(3.30)
6
⇒
ò
ï
b
χ(r) = r 1 + r2 + ..... ,
6
N
H
EC
E
U
IQ
(3.31)
où b est une constante déﬁnie par cette relation. Dans un espace localement plat, la
relation euclidienne entre les distances radiale et non-radiales s’applique
si la distance
2
radiale est suﬃsamment
petite,
|bχ
|
1,
c’est-à-dire
aχ
a(t)/
|b|.
Au
chapitre 4,
nous verrons que a(t)/ |b| est de l’ordre de ou plus grand que la distance de Hubble
H0−1 , ce qui explique pourquoi l’espace apparaît comme étant assez euclidien.
Pour compléter la métrique, nous devons maintenant combiner les distances radiale et non-radiale. Puisque nous supposons l’univers isotrope autour de l’origine,
la seule direction déﬁnie au point (χ, θ, φ) est la direction radiale. Cela implique que
la direction radiale doit être orthogonale aux surfaces de χ constant. Nous pouvons
alors faire encore usage du théorème de Pythagore pour trouver le temps de vol des
photons pour une direction arbitraire
(3.32)
dS 2 = a2 dχ2 + r(χ)2 (dθ2 + sin2 θdφ2 ) .
ÉC
E
L
O
T
Y
L
PO
Notons que le fait qu’il n’y ait pas de termes croisés, par exemple ∝ dtdχ, dans
cette expression provient de ce que nos horloges sont synchronisées. (Un terme croisé
donnerait des temps de vol qui dépendent de la direction de vol, ce qui impliquerait
que les horloges ne sont pas synchrones.) Notons que la synchronisation est simple
dans un univers homogène.
Il sera utile dans certains cas d’utiliser la fonction r(χ) elle-même comme coordonnée radiale sans dimension. En faisant usage de dr = dχ/χ (r), on trouve que,
dans le système de coordonnées (t, r, θ, φ), la métrique spatiale prend la forme
dS 2 = a2 f (r)dr2 + r2 (dθ2 + sin2 θdφ2 ) ,
(3.33)
où
ÉC
E
L
O
Y
L
PO
H
C
TE
f (r) = χ (r)2 = 1 + br2 + ..... .
U
Q
I
N
(3.34)
E
La métrique I : surtout l’isotropie
T
Y
L
PO
N
H
EC
E
U
IQ
129
La nature des deux coordonnées radiales se voit sur la métrique spatiale. La
coordonnée χ est directement reliée à la distance R entre l’origine et la surface
χ = constante :
ÉC
E
L
O
R(χ, t) = a(t)χ .
(3.35)
La coordonnée r est plus étroitement reliée aux distances non-radiales au travers de
(3.28). Il s’ensuit que la séparation angulaire ∆Θ entre deux observateurs comobiles
au même χ mais séparés d’une distance ∆S est au temps t
∆Θ =
∆S
.
a(t)r
(3.36)
La relation euclidienne ∆S = R∆Θ n’est respectée que si χ = r :
E
U
IQ
∆S
r
b
R2
=
= 1 − r2 + ....... = 1 −
+ ....... .
R∆Θ
χ
6
6a2 /b
N
H
EC
(3.37)
La relation euclidienne est une bonne approximation si R est suﬃsamment petit ;
R2 |a2 /b|.
Les distances non-radiales déterminent l’aire A de la surface χ = constante.
A(r, t) =
[a(t) r dθ] [a(t) r sin θdφ] = 4πr2 a(t)2
(3.38)
ÉC
E
L
O
T
Y
L
PO
ò
ï
Å ã
b
= 4πa2 χ2 1 −
χ2 + ..... .
3
(3.39)
Encore une fois, la relation euclidienne A = 4πR2 n’est respectée que si χ = r :
A
r2
b 2
R2
r
+ ....... .
=
=
1
−
+
.......
=
1
−
4πR2
χ2
3
3a2 /b
(3.40)
L’équation (3.38) suppose que sur la surface r = constante, les lignes de θ constant
sont perpendiculaires aux lignes de φ constant. C’est déjà implicite dans la façon
dont nous avons combiné dθ et dφ dans (3.28) pour construire dS. Cela implique
qu’il n’y a pas de distorsion de la forme d’un objet, par exemple une étoile cubique
convenablement orientée apparaîtrait dans le ciel comme un carré (Fig. 3.6). L’absence
de distorsion est une des caractéristiques d’un univers isotrope puisqu’il n’y a pas de
direction préférentielle dans laquelle les images puissent être déformées.
Comme nous manquons de mesures geométriques directes à grande échelle, on ne
peut restreindre la fonction r(χ) qu’en faisant des hypothèses supplémentaires. On
pourrait être tenté d’imposer la platitude, r(χ) = χ, mais, comme nous le verrons au
chapitre 4, cela équivaut à supposer que l’univers a une densité soit critique soit nulle.
Une hypothèse moins restrictive consiste à supposer que l’univers est homogène sur
le volume considéré, c’est-à-dire que tous les observateurs comobiles voient les mêmes
relations géométriques, comme (3.37) et (3.40). Nous allons voir que cette hypothèse
restreint r(χ) à l’une de trois formes possibles.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
130
ÉC
E
U
IQ
Chapitre 3. Coordonnées et métriques
E
L
O
T
Y
L
PO
N
H
EC
χ=χ
0
y
χ=0
θ
z
N
H
EC
E
U
IQ
T
Y
L
La métrique IIP:O
surtout l’homogénéité
E
L
O
C
É
Fig. 3.7: Coordonnées x, y, z centrées sur le point (χ0 , θ = 0) (x est perpendiculaire au plan
de la ﬁgure). Si le plan de la ﬁgure est plat, alors z = χ cos θ − χ0 ∼ χ − χ0 − χθ2 /2.
4
Les coordonnées (χ, θ, φ) ou (r, θ, φ) se rapportent à l’origine r = 0. Si la métrique spatiale (3.33) décrit un univers homogène, nous devrions pouvoir trouver des
coordonnées centrées en n’importe quel point dans lesquelles la métrique a la même
forme avec la même fonction f (r) ou r(χ). Si l’on peut toujours trouver de telles coordonnées, alors nous saurons que les relations géométriques comme (3.37) et (3.40)
s’appliquent partout.
Sans perte de généralité, nous allons construire un système de coordonnées (x, y, z)
centré sur le point (χ0 , θ = 0) comme sur la ﬁgure 3.7. Nous allons trouver qu’il suﬃt
de considérer une petite région centrée sur ce point.
En utilisant notre intuition d’un espace plat, on s’attendrait à ce qu’un bon choix
de coordonnées soit
x = r sin θ cos φ ,
z = χ cos θ − χ0
E
L
O
y = r sin θ sin φ
H
C
TE
χθ2
= χ − χ0 −
2
Y
L
PO
θ << 1 .
U
Q
I
N
(3.41)
(3.42)
Les terme en θ2 est, en première approximation, la correction au fait que les lignes
de θ constant font un angle θ avec l’axe z dans l’espace plat. Dans un espace courbe,
les lignes de θ constant font un angle α = θr (χ) avec l’axe z (ﬁgure 3.8). Pour cette
ÉC
E
La métrique II : surtout l’homogénéité
ÉC
E
L
O
T
Y
L
PO
z=χ1
y
χ= χ 1
θ=θ1
ÉC
N
H
EC
E
L
O
131
z=χ2
χ=χ 2
T
Y
L
PO
r1 θ1
E
U
IQ
N
H
EC
E
U
IQ
α=θ1 r (χ)
y= r1 θ1
r 2θ 1
θ=0
z=χ1
z=χ2
z
Fig. 3.8: Zoom de la ﬁgure 3.7 autour du point (x = y = z = 0). L’angle θ1 est petit et nous
pouvons donc utiliser la distance transverse au premier ordre rθ. Il y a un angle α = θr (χ)
entre les lignes de θ constant et l’axe z. Les lignes de χ constant sont perpendiculaires aux
lignes de θ constant et il y a donc le même angle α entre les lignes de χ constant et l’axe y.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
132
E
U
IQ
Chapitre 3. Coordonnées et métriques
T
Y
L
PO
N
H
EC
raison, la coordonnée suivante donne une métrique plus simple :
E
L
O
z = χ − χ0 −
rθ2 r (χ)
2
θ << 1 ,
(3.43)
qui revient au même que (3.42) si r = χ (espace plat). Pour comprendre la raison de
ce choix de z, on notera que puisque les surfaces de χ constant sont perpendiculaires
aux lignes de θ constant, l’angle entre les lignes de χ constant et l’axe y est aussi
α = θr (χ). Pour θ constant on s’attend donc à ce que dy = αdχ et pour χ constant à
ce que dz = αrdθ. Ces deux conditions sont satisfaites par les transformations (3.43)
et (3.41). Notons en particulier que si r (χ) = 0, alors z = χ− χ0 comme on s’y attend
puisque les lignes θ =constante sont parallèles à l’axe z dans ce cas.
Utilisant les transformations (3.41) et (3.43) la métrique spatiale (3.33) prend la
forme suivante au voisinage du point x = y = z = 0 (exercice 3.10) :
ÉC
dS 2 = a2 [dz 2 (1 − βx2 − βy 2 )
HN
E
U
IQ
+ dy 2 (1 − αy 2 ) + dx2 (1 − αx2 ) − 2αxydxdy] ,
C
E
T
LY
où les coeﬃcients α et β sont fonction de r0 :
O
P
E
L
ÉCO
α(r0 ) =
r0−2
β(r0 ) =
(f (r0 )−1 − 1)
f (r0 )
.
2r0 f 2 (r0 )
(3.44)
(3.45)
(3.46)
Remarquons avec une indéniable satisfaction que notre choix soigneux de coordonnées
donne une métrique localement euclidienne à l’origine, c’est-à-dire dS 2 = a2 (dx2 +
dy 2 + dz 2 ) aux corrections du second ordre près.
Si l’univers est homogène, la métrique (3.44) ne doit pas dépendre du choix de
l’origine : α(r) = constante et β(r) = constante. La solution de ces deux équations
est
f (r) =
1
,
1 − br2
(3.47)
où b est une constante arbitraire. Les espaces homogènes sont donc déﬁnis par la
valeur de b ; b = 0 correspond à un espace plat.
Alors que (3.47) est la solution de notre problème, nous remarquons que la métrique locale (3.44) en r = r0 ne ressemble pas à la métrique originale (3.33) en
r = 0. Pour se convaincre que la métrique originale (3.33) avec f (r) donné par (3.47)
représente un univers homogène, il faut trouver un changement de coordonnées qui
transforme la métrique locale (3.44) en (3.33). Cela est fait dans l’exercice 3.11.
La métrique complète pour un univers homogène et isotrope prend donc la forme
ï
ò
dr2
2
2
2
2
2
2
2
+ r (dθ + sin θdφ ) .
(3.48)
dτ = dt − a
1 − br2
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
La métrique II : surtout l’homogénéité
T
Y
L
PO
N
H
EC
E
U
IQ
133
On peut absorber
la constante b dans la déﬁnition du paramètre d’échelle a(t)
en
déﬁnissant a = a/ |b| et k = b/|b|. Après avoir fait la transformation r = |b|r
et en supprimant les « prime », on trouve la forme standard de la métrique de
Robertson-Walker :
ï
ò
dr2
2
2
2
2
2
2
2
+ r (dθ + sin θdφ ) ,
(3.49)
dτ = dt − a
1 − kr2
ÉC
E
L
O
où k = 0, ±1. Dans le système (χ, θ, φ) la métrique est


sin2 χ
χ2
(dθ2 + sin2 θdφ2 )
dτ 2 = dt2 − a2 dχ2 +
2
sinh χ
k=
+1
0 .
−1
La relation entre les deux coordonnées radiales est
r =
sin χ = χ − χ3 /6 + .....
χ
sinh χ = χ + χ3 /6 + .....
C
E
T
LY
E
U
IQ
+1
k= 0 .
−1
HN
(3.50)
(3.51)
La métrique spatiale est euclidienne pour r 1 (χ 1).
On voit qu’il y a trois types d’univers homogènes et isotropes correspondant à
k = 1, 0, −1. Au chapitre 4 nous verrons que ces trois cas correpondent à ΩT > 1,
ΩT = 1, et ΩT < 1.
Il est diﬃcile de se représenter des espaces tri-dimensionnels courbes, mais nous
allons essayer de nous en fabriquer une certaine intuition. Dans les cas k = 0 et k = 1,
les lignes de (θ, φ) constant divergent car r (χ) > 0 partout. Cela signiﬁe qu’il n’y a pas
de diﬀérence topologique évidente entre ces deux cas. En eﬀet, les diﬀérences dans la
relation angle-distance dépendent de notre choix d’horloges pour eﬀectuer les mesures
de distances radiales. Si l’on utilise des horloges comobiles, la géométrie spatiale du
cas k = −1 est non euclidienne. De l’autre côté, nous verrons dans la section 7 que si
l’on choisit des horloges du laboratoire, la géométrie spatiale peut être très diﬀérente.
En particulier, le cas k = −1 avec a(t) ∝ t représente un espace-temps plat avec
ΩT = 0.
Le cas k = 1 est plus intéressant car la distance entre des lignes de (θ, φ) constant
est proportionnelle à sin χ. Par conséquent ces lignes divergent pour ensuite reconverger et se rencontrer à χ = π. Le point à χ = π est appelé l’antipode de l’origine4 .
La situation est l’analogue tridimensionnel de la surface (bi-dimensionnelle) d’une
sphère de rayon a(t) plongée dans un espace à trois dimensions. À tout point de la
surface il correspond seulement un point à la distance aπ. La métrique sur la surface
d’une sphère a une forme très semblable à la métrique de Robertson-Walker pour
k = 1 (exercice 3.5). Il n’est peut-être pas surprenant qu’un univers k = 1 puisse être
considéré comme étant la « surface » d’une sphère tridimensionnelle plongée dans un
O
P
E
L
ÉCO
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
4 Nous verrons au chapitre 5 que si k = 1, notre antipode est très probablement au delà de notre
horizon, mais qu’il deviendra visible au moment où l’expansion sera maximum.
ÉC
E
134
11
00
11
00
χ=0
ÉC
E
U
IQ
Chapitre 3. Coordonnées et métriques
E
L
O
T
Y
L
PO
N
H
EC
λ1
1
0
1
0
χ1
Fig. 3.9: Un photon est émis à (χ1 , t1 ) avec une longueur d’onde λ1 . Il sera détecté plus
tard par nous à (χ = 0, t0 ) avec une longueur d’onde λ0 .
espace ayant quatre dimensions euclidiennes (exercice 3.6). Le lecteur souhaitant nous
imaginer comme des observateurs à quatre dimensions peut développer l’exercice 3.5.
On dit souvent qu’un univers k = 1 a un volume ﬁni correspondant à l’espace
χ < π. En fait, la métrique n’exclut pas la possibilité qu’il y ait des points plus
lointains de l’origine que πa. Elle nous dit seulement que l’espace χ > π est relié à
notre espace par un seul point, l’antipode de l’origine, ce qui fait qu’il est très diﬃcile
d’y aller.
Pour k = 1, le volume de l’univers (χ < π) peut se calculer :
π
π
2π
dχ
dθ
dφ sin2 χ sin θ = 2π 2 a3 ,
(3.52)
V = a3
0
T
Y
L
PO
0
0
N
H
EC
E
U
IQ
où nous avons fait usage de ce que les lignes de θ, φ, et χ constants sont perpendiculaires.
Enﬁn, il est important de se souvenir qu’il est possible que l’univers soit inhomogène à de très grandes échelles et que la métrique de Robertson-Walker ne soit
qu’une approximation commode au voisinage de notre position. Il est par conséquent
dangereux de tirer des conclusions « cosmiques » reposant sur sa forme.
ÉC
5
E
L
O
Propagation des photons
D’après la relativité générale, les particules suivent des géodésiques de l’espacetemps, c’est-à-dire des trajectoires qui sont des maxima locaux du temps propre. La
méthode générale pour trouver les géodésiques sera établie dans la section 7. Ici, nous
n’allons traiter que le cas des trajectoires les plus importantes en cosmologie, celles
des photons qui voyagent de galaxies lointaines vers nous, à l’origine. Ce problème est
particulièrement simple car on doit seulement imposer dτ = 0 le long de la tajectoire.
Considérons un photon (Fig. 3.9) émis à (t1 , χ1 , θ1 , φ1 ) puis détecté à (t0 , χ = 0).
En supposant que le photon suive un chemin de θ et φ constants (ce qui sera justiﬁé
en section 7), la métrique (3.50) implique
dχ = 1 .
(3.53)
dt a(t)
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
La dérivée par rapport au temps de χ augmente si a(t) diminue car la distance physique dS entre des points comobiles décroît.
ÉC
E
Propagation des photons
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
T
Y
L
PO
E
U
IQ
N
H
EC
135
E
U
IQ
Fig. 3.10: Trajectoire χ(t) d’un photon qui arrive à l’origine à t0 calculée par (3.53). Le
temps (axe vertical) est paramétrisé par â(t). La trajectoire est dessinée pour trois des combinaisons de (ΩM , ΩΛ ) de la ﬁgure 1.9. La plupart du ∆χ total est traversée à des temps
précoces (a(t) petit) car les distances entre des points comobiles étaient petites à ce moment.
La ﬁgure montre une corrélation importante entre la distance actuelle d’une source de photons de redshift donné et le paramètre de décélération q0 = ΩM /2 − ΩΛ . Considérons un
photon émis à â1 = 0.5 ce qui correspond à un redshift (z + 1 = 2). On voit sur la ﬁgure que
la distance actuelle de la source est a0 χ1 ∼ 0.6H0−1 si (ΩT = ΩM = 1 ⇒ q0 = 0.5). La distance actuelle est a0 χ1 ∼ 0.75H0−1 si (ΩM = 0.3, ΩΛ = 0.7 ⇒ q0 = −0.55). Cette corrélation
est due à ce qu’un univers en décélération a eu un taux d’expansion relativement rapide dans
le passé ce qui implique un temps écoulé relativement faible pour une valeur donnée de a1 /a0 .
Il en résulte que, pour (q0 > 0), un photon parcourt une distance comobile relativement petite
a0 (χ(t1 ) − χ(t0 )) comparée à celle d’un univers en accélération (q0 < 0). En raison de la distance accrue, il n’est pas étonnant que l’on trouve, comme nous le verrons dans la section 6,
que les objets de redshift donné apparaissent moins brillants dans un univers en accélération
que dans un univers en décélération.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
136
E
U
IQ
Chapitre 3. Coordonnées et métriques
T
Y
L
PO
N
H
EC
En intégrant sur le chemin du photon, on trouve une relation entre (t1 , χ1 ) et t0 :
t0
dt
χ1 =
.
(3.54)
a(t)
t1
E
L
O
Cette équation déﬁnit le « cône de lumière » associé au point (t0 , χ = 0), c’est-à-dire
l’instant t1 auquel nous voyons des galaxies à χ1 . On peut évaluer χ1 si l’on connaît
a(t) qui est déterminé par l’équation de Friedmann, et nous le ferons en détail au
chapitre 5. Dans la ﬁgure 3.10 nous montrons les trajectoires des photons pour trois
valeurs de l’ensemble (ΩM , ΩΛ ) en utilisant la fonction a(t) de la ﬁgure 1.9.
Pour des galaxies proches, on peut négliger la variation de a(t) pendant le vol des
photons. Dans ce cas, on trouve
ÉC
a 0 χ1 ∼ t 0 − t 1
t0 − t 1 t H .
(3.55)
E
U
IQ
Cette expression dit simplement que le temps de vol est égal à la distance.
La relation (3.54) détermine aussi le redshift d’une galaxie en fonction de χ1 . Considérons encore notre photon émis par une galaxie à (t1 , χ1 , θ1 , φ1 ) avec une longueur
d’onde λ1 . On peut traiter ce photon comme une onde électromagnétique classique
et appliquer (3.54) à deux crêtes consécutives. La première crête quitte χ1 à t1 et
la seconde quitte χ1 à t1 + λ1 /c. Les deux crêtes sont détectées, respectivement, à
(t0 , χ = 0) et (t0 + λ0 /c, χ = 0). L’équation (3.54) donne
t0 +λ0
t0 t1 +λ1 t0 +λ0
t0
dt
dt
=
=
χ1 =
−
+
.
(3.56)
t1 a(t)
t1 +λ1 a(t)
t1
t1
t0
ÉC
E
L
O
T
Y
L
PO
N
H
EC
En négligeant la variation de a(t) sur une période λ/c, nous trouvons une expression
élégante pour le redshift
z+1 ≡
λ0
a0
=
.
λ1
a1
(3.57)
On voit que le photon a une « expansion » du même facteur que celle de l’univers.
Cela conﬁrme la loi que nous avons montrée dans la section 2.4 du chapitre 1.
Pour des sources proches, nous pouvons développer a(t) en série de Taylor (2.5) :
ô
ñ
ã
Å
q0 t − t0 2
t − t0
a(t) = a0 1 +
−
+ ..... .
tH
2
tH
En substituant les deux premiers termes dans (3.57) on trouve
z ∼ H0 (t0 − t1 ) ∼ H0 χ1 a0
H
C
E
U
Q
I
N
(t0 − t1 ) tH .
T
Y
POL
(3.58)
C’est tout simplement la loi de Hubble (1.14) puisque z ∼ v/c pour z 1.
En utilisant (3.57), nous pouvons maintenant trouver une expression pour χ1 en
fonction du redshift en faisant un changement de variables dans (3.54) :
a0
da
χ1 (z) =
.
(3.59)
a0 /(1+z) aȧ
ÉC
E
L
O
E
Distance de luminosité et distance angulaire
T
Y
L
PO
N
H
EC
E
U
IQ
137
Cette expression est plus utile que (3.54) car le redshift d’une galaxie peut être mesuré
alors que l’instant d’émission ne peut pas l’être.
Une fois de plus, nous faisons usage du développement de Taylor (2.5) de a(t),
cette fois au second ordre :
a0
da
.
(3.60)
χ1 (z) ∼
a0 /(1+z) a a0 H0 [1 − q0 H0 (t − t0 )]
ÉC
E
L
O
Utilisant H0 (t − t0 ) ∼ (a/a0 − 1) 1, on trouve
ò
ï
1 + q0
z + .....
a0 χ1 (z) = H0−1 z 1 −
2
z1.
(3.61)
Le résultat du premier ordre a0 χ1 (z) = H0−1 z est la loi de Hubble. La correction
entre crochets dépend du paramètre de décélération q0 et nous en ferons usage au
chapitre 5 aﬁn de contraindre les paramètre cosmologiques. Le fait que la distance
a0 χ1 soit une fonction décroissante de q0 a une explication simple illustrée sur la
ﬁgure 3.10. Un redshift donné correspond à un facteur d’expansion donné a0 /a1 entre
l’émission et l’absorption. La décélération implique une expansion rapide (dans le
passé) ce qui diminue le temps de l’expansion entre a1 et a0 et, par conséquent, le
temps de vol. Un temps de vol moindre signiﬁe une distance a0 χ1 moindre entre la
source et l’observateur.
Nous remarquons que puisque r ∼ χ + O(χ3 ) et χ ∝ z + O(z 2 ), (3.61) s’applique
aussi à r1 :
ò
ï
1 + q0
z + .....
z1.
(3.62)
a0 r1 (z) = H0−1 z 1 −
2
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
Nous terminerons cette section en établissant un résultat nécessaire pour le calcul
des ﬂux de photons de galaxies lointaines. Considérons une source qui émet deux
photons, l’un à (t1 , χ1 ) et l’autre plus tard à (t1 + ∆t1 , χ1 ). Les deux photons seront
détectés par nous à (t0 , χ = 0) et (t0 + ∆t0 , χ = 0). En appliquant la même analyse
à ces deux photons qu’aux crêtes d’ondes ci-dessus, on trouve
∆t0
a0
=
= z+1.
∆t1
a1
(3.63)
On voit qu’une impulsion de photons va s’étendre en temps par le paramètre d’expansion. Cet eﬀet a été conﬁrmé par des mesures de durées apparentes d’explosions de
supernovae de grand redshift [115]. La raison physique de cette « dilatation cosmique
du temps » est simplement que, pour atteindre l’observateur, chaque photon doit
parcourir une distance plus grande que le photon précédent.
6
Y
L
PO
H
C
TE
U
Q
I
N
Distance de luminosité et distance angulaire
E
L
O
Nous possédons maintenant tous les concepts nécessaires pour calculer les ﬂux
de photons et les distances angulaires, concepts indispensables pour interpréter les
ÉC
E
138
E
U
IQ
Chapitre 3. Coordonnées et métriques
T
Y
L
PO
N
H
EC
observations astronomiques. Comme dans la section précédente, nous considérons une
source de photons de luminosité L et de coordonnée radiale χ1 . Sur un temps ∆t1
centré en t1 , le source émet N photons d’énergie moyenne E1 avec L = N E1 /∆t1 .
Comme l’illustre la ﬁgure 3.11, à t0 les photons sont distribués sur la surface d’une
sphère de rayon a0 χ1 centrée sur la source. L’aire de cette surface est 4πa20 r12 . Les
photons ont maintenant une énergie moyenne E0 = E1 a1 /a0 et mettent un temps
∆t0 = ∆t1 a0 /a1 pour traverser la surface. Le ﬂux d’énergie est donc
ÉC
E
L
O
φ =
N E0
N E1 /∆t1
L
=
=
,
2
2
2
2
2
4πa0 r1 ∆t0
4πa0 r1 (1 + z)
4πd2L
(3.64)
où cette relation déﬁnit la « distance de luminosité » de la source à χ1
dL = a0 r1 (1 + z) .
(3.65)
E
U
IQ
Les équations (3.64) et (3.65) généralisent la loi habituelle des ﬂux en « 1/R2 ». La
nouvelle loi tient compte de la taille de la sphère entourant la source, du redshift de
l’énergie des photons, et de la dilatation cosmologique du temps. Pour des sources
proches, on peut utiliser (3.61) pour r1 ce qui donne
ò
ï
1 + q0
z + ..... (1 + z)
(3.66)
dL (z) = H0−1 z 1 −
2
ÉC
E
L
O
T
Y
L
PO
N
H
EC
ò
ï
1 − q0
= H0−1 z 1 +
z + ..... .
2
(3.67)
Comme avec la distance a0 χ1 , et pour les mêmes raisons, la distance de luminosité
est une fonction décroissante de q0 . Pour un redshift donné, les objets apparaissent
plus brillants dans un univers en décélération que dans un univers en accélération.
La deuxième formule dont nous avons besoin pour les observations astronomiques
est celle qui relie la taille d’un objet et sa taille angulaire vue sur le ciel. Dans la ﬁgure
3.12 nous montrons deux points de coordonnée radiale χ1 séparés par une distance
∆S à t1 . La séparation angulaire ∆Θ = (dθ2 + sin2 θdφ2 )1/2 est déterminée par la
métrique (3.33) ce qui donne ∆S = a1 r1 ∆Θ. Un photon est émis de chaque point à
t1 et détecté ultérieurement à (t0 , χ = 0). Pendant leur voyage jusqu’à l’observateur
à χ = 0, les deux photons suivent des chemins de (θ, φ) constants, et les photons sont
donc observés sous l’angle original
∆Θ =
∆S
∆S
=
.
a1 r1
dA
T
Y
POL
Cette relation déﬁnit la « distance angulaire »
E
L
O
dA = a1 r1 =
ÉC
dL
.
(1 + z)2
H
C
E
U
Q
I
N
(3.68)
(3.69)
La distance angulaire est nécessairement plus petite que la distance de luminosité.
E
Distance de luminosité et distance angulaire
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
139
χ1
χ=0
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
Fig. 3.11: Des photons émis à (t1 , χ1 ) sont, à t0 , dispersés sur la surface d’aire 4πa20 r12
d’une sphère de rayon a0 χ1 .
r=0
∆Θ
Y
L
PO
U
Q
I
N
∆S= a 1 r 1 ∆Θ
H
C
TE
Fig. 3.12: Des photons émis à (t1 , χ1 ) par un objet de taille ∆S = a1 r1 ∆Θ. Pendant leur
voyage vers l’origine, les photons suivent des chemins de (θ, φ) constants et vont être observés
avec une séparation angulaire ∆Θ = ∆S/(a1 r1 ).
ÉC
E
L
O
E
140
7
E
U
IQ
Chapitre 3. Coordonnées et métriques
N
H
EC
L’équation des géodésiques
T
Y
L
PO
En l’absence de forces non-gravitationnelles, une particule suit une trajectoire qui
maximise son temps propre. Une telle trajectoire est appelée géodésique d’espacetemps. Dans cette section, nous allons trouver l’équation générale des géodésiques et
l’appliquer à la métrique de Robertson-Walker .
Considérons un espace-temps à quatre dimensions couvert par un système de coordonnées xµ , µ = 0, 1, 2, 3 et caractérisé par une métrique gµν :
ÉC
E
L
O
dτ 2 = gµν dxµ dxν .
(3.70)
La trajectoire d’une particule peut être déﬁnie soit par trois fonctions xi (x0 ), i = 1, 2, 3
donnant la position spatiale en fonction de la coordonnée de temps, ou bien par quatre
fonctions xµ (τ ), µ = 0, 1, 2, 3 donnant les coordonnées de la particule en fonction de
son temps propre. Dans le deuxième cas, la métrique impose une contrainte sur les
dérivées premières :
1 = gµν
N
H
EC
dxµ dxν
.
dτ dτ
T
Y
L
PO
E
U
IQ
(3.71)
On ne peut pas utiliser τ pour paramétriser la trajectoire de particules de masse nulle,
et ce cas nécessite un traitement particulier.
Considérons une géodésique xµ (τ ) entre les points d’espace-temps A et B. Le
temps propre écoulé entre A et B est donné par
ÉC
E
L
O
B
τAB =
»
gµν (x)dxµ dxν .
(3.72)
A
Considérons maintenant une non-géodésique entre A et B déﬁnie par xµ (τ ) + µ (τ ) où
τ est le temps propre le long de la géodésique xµ (τ ) à partir du point A. Cette nongéodésique a les mêmes extrêmités, par conséaquent nous imposons (0) = (τAB ) = 0.
Le temps propre le long de la non-géodésique est
τAB
B
=
»
gµν (x + ) (dxµ + dµ ) (dxν + dν ) .
A
(3.73)
U
Q
I
N
Si les fonctions xµ (τ ) décrivent des géodésiques, le temps propre τAB doit être
stationnaire par rapport à de petites variations (τ ) :
H
C
TE
− τAB = 0 + O(2 ) .
τAB
Y
L
PO
(3.74)
Nous pouvons ainsi calculer τAB
au premier ordre en utilisant
ÉC
E
L
O
gµν (x + ) = gµν (x) +
ï
∂gµν
∂xλ
ò
λ .
x
(3.75)
E
L’équation des géodésiques
T
Y
L
PO
N
H
EC
E
U
IQ
141
En ne retenant que les termes d’ordre , le temps propre le long de la non-géodésique
est
Bï
ò1/2
∂gµν λ µ ν
µ ν
τAB =
dx
dx
+
2g
dx
d
,
(3.76)
gµν dxµ dxν +
µν
∂xλ
A
ÉC
E
L
O
Où nous avons fait usage de la symétrie de la métrique pour identiﬁer gµν dxµ dν et
gµν dxν dµ . En factorisant le terme du premier ordre, nous obtenons
τAB
B
ν 1/2
µ
=
[gµν dx dx ]
A
ï
ò
∂gµν λ dxµ dxν
dxµ dν 1/2
1+
+ 2gµν
,
∂xλ
dτ dτ
dτ dτ
(3.77)
où nous avons fait usage de la relation dτ 2 = gµν dxν dxµ aﬁn de simpliﬁer la forme
de la seconde racine carrée. En développant cette racine carrée et en ne gardant que
les termes linéaires en on obtient
B
=
[gµν dxµ dxν ]1/2
τAB
A
B
ν 1/2
µ
+
[gµν dx dx ]
A
T
Y
L
PO
ñ
E
L
O
N
H
EC
1 ∂gµλ ν dxµ dxλ
dν dxµ
+
gµν (x)
dτ dτ
2 ∂xν
dτ dτ
E
U
IQ
ô
.
(3.78)
En utilisant à nouveau dτ 2 = gµν dxµ dxν , ceci n’est que
ô
B ñ
1 ∂gµλ ν dxµ dxλ
dν dxµ
+
τAB = τAB +
dτ gµν (x)
dτ dτ
2 ∂xν
dτ dτ
A
ÉC
B
= τAB +
A
B
−
ñ
d
dτ dτ
ν
A
Å
d
dτ
dτ
ã
Å
dxµ ν
gµν (x)
dτ
dxµ
gµν (x)
dτ
ã
1 ∂gµλ dxµ dxλ
− 2 ∂xν dτ dτ
ô
ν
U
Q
I
N
La première intégrale s’annule car (0) = (τAB ) = 0. Puisque la fonction est
arbitraire, la deuxième intégrale est nulle seulement si xµ (τ ) satisfait l’équation :
Å
ã
1 ∂gµλ dxµ dxλ
d
dxµ
gµν (x)
−
= 0
ν = 0, 1, 2, 3 .
(3.79)
dτ
dτ
2 ∂xν dτ dτ
Y
L
PO
H
C
TE
Cette équation est appelée « équation des géodésiques ». Elle détermine la trajectoire
de particules en l’absence de forces non-gravitationnelles.
Pour la métrique de Robertson-Walker
dτ 2 = dt2 − a2 (t) dχ2 + r(χ)2 (dθ2 + sin2 θdφ2 ) ,
(3.80)
ÉC
E
L
O
E
142
E
U
IQ
Chapitre 3. Coordonnées et métriques
T
Y
L
PO
N
H
EC
le chemin d’une particule est déterminé par quatre fonctions, t(τ ), χ(τ ), θ(τ ) et φ(τ ).
La métrique (3.80) impose une contrainte sur la dérivée première des quatre fonctions :
E
L
O
2
t − a2 χ2 − a2 r2 (θ2 + sin2 θφ2 ) = 1 ,
(3.81)
où χ = dχ/dτ , etc. Les quatre équations de la géodésique (3.79) sont :
Å
ã
r
d 2 ȧ 2
(θ2 + sin2 θφ2 ) ,
= a2
a χ = a χ + 2 tχ
dτ
a
f (r)
ÉC
φ =
θ =
−2 2 ȧ
rφ −
θ φ − 2 t φ ,
r
tan θ
a
−2 ȧ
r θ + sin θ cos θφ2 − 2 t θ ,
r
a
N
H
EC
t = −aȧ[χ2 + r2 (θ2 + sin2 θφ2 )] .
T
Y
L
PO
(3.82)
(3.83)
E
U
IQ
(3.84)
(3.85)
Trois types de solutions de ces équations sont particulièrement intéressantes pour
la cosmologie :
E
L
O
– « Mouvement galactique ». les solutions χ = constant, φ = constant, θ =
constant, t = τ , correspondent au mouvement attendu des galaxies dans des
coordonnées comobiles.
ÉC
– Mouvement radial. Les conditions initiales θ = φ = 0 impliquent θ = φ = 0.
Il en découle que le mouvement purement radial entre une galaxie et l’origine
est solution, comme nous l’avons supposé dans la section 5. Dans le cas d’un
mouvement radial, l’équation pour χ est particulièrement simple :
d 2 a χ = 0 ⇒ a2 χ = constante .
dτ
(3.86)
U
Q
I
N
– Mouvement radial de photons. Les équations (3.82), (3.83), (3.84), (3.85), et
(3.86) ne peuvent pas s’appliquer directement aux photons puisque dτ = 0 pour
une particule de masse nulle, ce qui implique que τ ne peut pas paramétriser
leurs trajectoires. Toutefois, nous pouvons combiner (3.86) et (3.85) pour obtenir
une équation pour χ(t) :
E
L
O
Y
L
PO
H
C
TE
ȧ
χ̈ = −2 χ̇ + aȧχ̇3 ,
a
(3.87)
où le point signiﬁe d/dt. La solution aχ̇ = 1 = c de cette équation est cohérente
avec la déﬁnition de dχ, (3.23) et (3.22).
ÉC
E
Eﬀet de lentille gravitationnelle
8
N
H
EC
E
U
IQ
143
Eﬀet de lentille gravitationnelle
T
Y
L
PO
Comme application des équations du mouvement générales trouvées à la section
précédente, nous allons traiter le cas d’un potentiel gravitationnel Φ(r) à symétrie
sphérique. Pour Φ(r)/c2 1 la métrique est donnée par 5 (3.17) :
ÉC
E
L
O
dτ 2 ∼ dt2 [1 + 2Φ(r)/c2 ] − [1 − 2Φ(r)/c2 ] dr2 /c2 ,
(3.88)
ou
dτ 2 ∼ dt2 [1 + 2Φ(r)/c2 ] − [1 − 2Φ(r)/c2 ] [dx2 + dy 2 + dz 2 ]/c2 .
(3.89)
(Dorénavant nous supprimons les facteurs c.) Comme toujours, il faut être prudent
et déﬁnir de façon opératoire les coordonnées. Une horloge à un endroit ﬁxe peut
déterminer la coordonnée temporelle t en utilisant
dτ ∼ dt [1 + Φ(r)]
dr = 0 .
N
H
EC
E
U
IQ
(3.90)
Les coordonnées spatiales peuvent être déterminées à partir du temps de vol de photons, par exemple
T
Y
L
PO
dr ∼ dt [1 + 2Φ(r)]
E
L
O
dτ = 0 .
(3.91)
Le potentiel Φ dont on a besoin dans ces relations peut être déterminé à partir du
redshift gravitationnel, comme l’illustre la ﬁgure 3.13.
L’utilisation cosmologique la plus importante de cette métrique est l’eﬀet de lentille
gravitationnelle sur les objets lointains. Cet eﬀet provient de l’eﬀet gravitationnel sur
les trajectoires des photons comme l’illustre la ﬁgure 3.14.
Pour calculer la trajectoire d’un photon, nous devons résoudre les équations du
mouvement pour des photons dans un champ gravitationnel. Appliquons l’équation
des géodésiques pour des particules massives (3.79) à la métrique (3.89). Pour cette
métrique indépendante du temps, l’équation pour µ = 0 est simple :
ï
ò
A
dt
A
dt
d
=
,
(3.92)
=
g00
= 0
⇒
dτ
dτ
dτ
g00
1 + 2Φ(r)
ÉC
U
Q
I
N
où A est une constante (qui s’élimine au bout du compte). L’équation pour i = 1, 2, 3
est plus compliquée :
ï
ò
∂gµµ Å dxµ ã2
d
dxi
= 0.
(3.93)
gii
− (1/2)
dτ
dτ
∂xi
dτ
µ
Y
L
PO
H
C
TE
Cette équation ne s’applique pas aux photons pour lesquels dτ = 0. On peut cependant utiliser (3.92) pour remplacer τ par t pour obtenir une équation applicable aux
E
L
O
5 Pour une masse ponctuelle, la métrique (3.88) est une permière approximation de la célèbre
métrique de Schwarzschild, g00 = (1 + 2Φ) et grr = −(1 + 2Φ)−1 .
ÉC
E
144
t
ÉC
E
U
IQ
Chapitre 3. Coordonnées et métriques
10E
L
O
T
Y
L
PO
N
H
EC
5
ÉC
T
Y
L
PO
E
L
O
r
1
N
H
EC
E
U
IQ
r2
r
Fig. 3.13: L’échange de photons (lignes diagonales) entre deux horloges, l’une en r1 et l’autre
en r2 dans un potentiel Φ(r). Les « clics
r » des horloges sont représentés par les petits traits
dr(1 − 2Φ) de façon que les trajectoires des photons
horizontaux. L’axe spatial donne r =
apparaissent comme des lignes droites. L’horloge 2 est suﬃsamment éloignée de l’origine
pour que Φ(r2 ) ∼ 0 et l’horloge mesure la coordonnée t, dt = dτ . Cela peut se voir par le
fait qu’à t = 5, l’horloge en r2 a cliqué 5 fois. L’horloge 1 est dans le puits de potentiel et
nous choisissons Φ(r1 ) = −0.2. (nous négligeons les termes d’ordre Φ2 = 0.04 !) En r1 on
a dτ = (1 − 0.2)dt = 0.8dt et, à cause de cela, l’horloge n’a cliqué que 4 fois à t = 5. À
chaque clic, l’horloge envoie un photon à l’autre horloge. À partir des temps d’arrivée mesurés par l’horloge 2, un observateur en r2 constate que l’horloge 1 retarde (4 photons reçus
pour 5 clics). De la même façon, un observateur en r1 voit que l’horloge 2 avance (5 photons
reçus pour 4 clics). Des observateurs aux deux endroits peuvent déterminer la diﬀérence de
potentiel par cet eﬀet. Si on l’applique à des crêtes d’ondes électromagnétiques classiques, ce
raisonnement peut démontrer le redshift et le blueshift gravitationnel de photons individuels,
∆ν/ν = ∆Φ. On dit souvent que des photons « perdent de l’énergie » lorsqu’ils s’échappent
de puits de potentiel. Mais cette démonstration montre que le redshift gravitationnel est plutôt
relié à la diﬀérence du mouvement (d’horlogerie) des horloges dans des potentiels gravitationnels. En dépit de cela, il est diﬃcile d’éviter de parler de perte d’énergie des photons, de
la même façon que l’on dit que les photons perdent de l’énergie par le redshift cosmologique.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Eﬀet de lentille gravitationnelle
T
Y
L
PO
y
ÉC
E
L
O
α
N
H
EC
E
U
IQ
145
b
z
Fig. 3.14: La déﬂexion d’un photon dans un potentiel gravitationnel Φ(r). La plus proche
distance d’approche du photon à r = 0 (en l’absence de déﬂexion) est le « paramètre d’impact » b. L’angle de déﬂexion α dépend de la forme du potentiel et, en général, de b, par
exemple (3.100) ou (3.101).
photons :
T
Y
L
PO
N
H
EC
E
U
IQ
ò
ï
∂gµµ Å dxµ A ã2
A d
dxi A
− (1/2)
gii
= 0,
g00 dt
dt g00
∂xi
dt g00
µ
ou encore
ÉC
E
L
O
d
dt
ï
dxi gii
dt g00
ò
=
Å
ã
1 ∂Φ dxµ 2
.
g00 ∂xi µ
dt
(3.94)
(3.95)
Considérons la situation illustrée sur la ﬁgure 3.14 avec le photon incident dans la
direction z dans le plan yz. Sans déﬂexion, la trajectoire serait simplement
dz
= 1
dt
y(t) = b ,
(3.96)
où b est le paramètre d’impact. Puisque l’angle de diﬀusion est très petit, on peut
négliger tout facteur proportionnel à dy/dt dans (3.95). Dans ce cas, l’équation selon
y est
ñ
Å ã2 ô
dz
∂Φ
∂Φ
1+
.
(3.97)
∼ 2
gyy ÿ ∼
∂y
dt
∂y
H
C
TE
Puisque Φ 1, on peut prendre gyy ∼ −1 ce qui donne
Y
L
PO
ÿ ∼ −2
E
L
O
∂Φ
.
∂y
U
Q
I
N
(3.98)
Cette « accélération transverse » est exactement double de ce qu’aurait donné un
simple argument newtonien.
ÉC
E
146
E
U
IQ
Chapitre 3. Coordonnées et métriques
T
Y
L
PO
N
H
EC
La variation transverse de la vitesse est égale à l’angle de déﬂexion α :
∞
∞
∂Φ
dz .
α = ∆vy /c =
ÿdt = 2
−∞
−∞ ∂y
E
L
O
(3.99)
Deux potentiels sont particulièrement intéressants. Le premier est celui d’un objet
ponctuel de masse M :
ÉC
GM
∂Φ
=
∂r
r2
⇒
α =
4GM
.
bc2
(3.100)
L’angle de déﬂexion est de l’ordre du potentiel gravitationnel Φ(b) à la distance d’approche minimale, ou, de façon équivalente, le carré de la vitesse circulaire vc2 /c2 d’un
objet massif en orbite à la distance d’approche minimale.
Le second potentiel qui va nous intéresser donne une vitesse de rotation constante
et constitue une bonne approximation pour des objets étendus comme les halos galactiques ou les amas de galaxies :
v2
∂Φ
= c
∂r
r
T
Y
L
PO
⇒
N
H
EC
α = π
vc2
.
c2
E
U
IQ
(3.101)
Ici, vc est la vitesse circulaire (constante) d’objets en orbite dans la galaxie ou dans
l’amas.
Comme l’illustre la ﬁgure 3.15, la déﬂexion gravitationnelle peut créer deux images
d’une source. Les deux images ont des paramètres d’impact b1 et b2 . Le potentiel d’une
masse ponctuelle donne toujours deux images parce que l’angle de déﬂexion diverge
pour de faibles paramètres d’impact. Nous verrons plus bas que l’une des images est
en général beaucoup plus lumineuse que l’autre.
D’un autre côté, dans le cas de la déﬂexion angulaire constante d’un amas de
galaxies (3.101), il y aura deux images séparées par un angle α seulement sur le
paramètre d’impact non-déﬂéchi satisfait b0 < bmax = Lα/2 où L est la distance
entre la source et la lentille (que nous prenons égale à la distance observateur-lentille
pour simpliﬁer). La raison en est que si b0 > Lα/2, les deux images devraient être du
même côté de l’amas ce qui est, bien évidemment, impossible.
La grands amas ont α = vc2 /c2 ∼ 10−5 ce qui fait que les deux images peuvent
être résolues par des télescopes terrestres qui ont une résolution σθ ∼ 3 × 10−6 .
La « section eﬃcace » pour qu’il y ait une image double est σ ∼ πb2max =
πL2 vc2 /c2 . Cette section eﬃcace augmente avec L car l’angle de déﬂexion nécessaire
décroît avec L.
La probabilité qu’un objet donné ait deux images à cause de l’eﬀet de lentille dû à
un amas de galaxies est simplement la probabilité P que l’objet se cache derrière un
amas. Cette probabilité est proportionnelle à la section eﬃcace, au nombre volumique
d’amas n, et à la longueur totale du chemin ∼ L :
ÉC
E
L
O
ÉC
E
L
O
Y
L
PO
P ∼ 2Lnσ ∝ L3 .
H
C
TE
U
Q
I
N
(3.102)
E
Eﬀet de lentille gravitationnelle
LY T
N
H
EC
y
L
O
P
E
L
É Co O
E
U
IQ
147
L
2θ1
observer
b1
source
s
b0
z
b2
2θ 2
N
H
EC
E
U
IQ
Fig. 3.15: Création de deux images d’une source S par un potentiel gravitationnel symmé-
trique autour de l’origine. Le paramètre d’impact non déﬂéchi est b0 alors que les trajectoires
physiques des photons ont des paramètres d’impact b1 et b2 et des angles de déﬂexion α1 = 2θ1
et α2 = 2θ2 . Pour simpliﬁer, la source et l’observateur O sont à égale distance de l’origine.
Les angles ont été très exagérés pour la clarté de la ﬁgure.
E
L
O
T
Y
L
PO
Le fait que la probabilité croisse rapidement avec L rend le nombre de quasars à deux
images sensible à la valeur de q0 , comme nous le verrons dans la section 2.
Une seconde application de la déﬂexion par les amas vient de ce que les temps de
vol pour les deux images ne sont pas égaux. Les quasars ont une variabilité intrinsèque
et en comparant les courbes de lumière (ﬂux en fonction du temps) des deux images,
on détermine la diﬀérence ∆t des deux temps de vol.
Pour calculer ∆t, on impose dτ = 0 sur la métrique (3.89) :
ñ
Å ã ô
1 dy 2
dt ∼ dz 1 − 2Φ +
.
(3.103)
2 dz
ÉC
Le délai en temps est la diﬀérence entre les intégrales évaluées sur les deux chemins.
Le terme du premier ordre dz s’annule manifestement, laissant un terme « gravitationnel » proportionnel à la diﬀérence de potentiel et un terme « geométrique »
proportionnel à la diﬀérence dans (dy/dz)2 . Pour un angle de déﬂexion indépendant
du point d’impact, ce qui est approximativement le cas pour les amas de galaxies
(3.101), le terme geométrique s’annule laissant
∞
∆t ∼ 2
dz [Φ(y2 (z)) − Φ(y1 (z))] ,
(3.104)
−∞
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
où y1 (z) et y2 (z) sont les trajectoires des photons dans les deux images. Considérons
le cas presque symétrique, |y1 | ∼ |y2 |. En nous reportant à la ﬁgure 3.15, on voit que
ÉC
E
148
E
U
IQ
Chapitre 3. Coordonnées et métriques
N
H
EC
dans le cas où θ1 ∼ θ2 = θ on a b1 − b0 = b2 + b0 . L’intégrale sera dominée par la
région proche de l’amas et nous pouvons faire l’approximation :
E
L
O
T
Y
L
PO
|y1 (z)| − |y2 (z)| ∼ b1 − b2 ∼ 2b0 .
(3.105)
En substituant cela dans (3.104), on a
ÉC
∆t ∼ 4b0
∞
dz
−∞
∂Φ
.
∂y
(3.106)
L’intégrale est tout simplement l’angle de déﬂexion 2θ donné par (3.99), et le délai en
temps est
∆t = 4L
b0
2θ .
L
E
U
IQ
(3.107)
N
H
EC
Le facteur b0 /L est la séparation angulaire entre le centre de l’amas et la position
moyenne des deux images.
Pour estimer la longueur du délai, on peut prendre b0 /L ∼ θ ∼ 10−5 et L ∼ dH
ce qui donne ∆t ∼ 1 an.
Dans (3.107), l’angle de déﬂexion 2θ peut être déterminé à partir de la séparation
angulaire des deux images. L’angle b0 /L est plus diﬃcile à déterminé car il demande de
connaître la distribution de masse de l’amas. Cette distribution peut être déterminée
à partir de la distorsion du fond de galaxies (voir ci-dessous).
Une fois connus les deux angles θ et b0 /L, la distance L de l’amas peut être
déterminée à partir de la valeur mesurée de ∆t. La connaissance du redshift de l’amas
détermine alors H0 , comme nous l’avons déjà dit au chapitre 2 dans la section 5.1.
Le précision de cette méthode de détermination de H0 est limitée par la diﬃculté de
déterminer la distribution de masse de l’amas.
Le dernier eﬀet de lentille gravitationnelle vient de la distorsion de l’image d’un
objet étendu. La distorsion dans les directions radiale et tangentielle est illustrée sur
la ﬁgure 3.16. C’est cette distorsion qui mène aux arcs que l’on peut voir sur la ﬁgure
2.13. Les arcs visibles sont proches d’un cercle de rayon angulaire α autour du centre
de l’amas. Les galaxies du fond plus loin du centre de l’amas auront une seule image
faiblement distordue. Statistiquement, elles apparaîtront allongées suivant les cercles
équipotentiels de l’amas. Cet eﬀet d’alignement des galaxies par une « lentille faible »
peut être utilisé pour déterminer la masse de l’amas. Les masses déterminées de cette
façon peuvent être comparées avec les masses déterminées à partir de la dispersion en
vitesse et à partir de l’émission de rayons X.
Même lorsque les galaxies du fond ne sont pas aﬀectées par un amas plus proche,
le chemin des photons peut quand même être aﬀecté par le potentiel gravitationnel
aléatoire dû aux inhomogénéités de masse. Cela mène à de petites corrélations dans
l’orientation apparente des galaxies dans la même direction angulaire. Cet eﬀet n’a été
observé que récemment [117] et sera un outil important pour sonder les inhomogénéités
à grande échelle.
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Eﬀet de lentille gravitationnelle
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
y
image 1
y
s
o
ÉC
E
U
IQ
b1
z
E
L
O
149
T
Y
L
PO
N
H
EC
b0
x
b2
image 2
Fig. 3.16: L’eﬀet de lentille gravitationnelle d’un potentiel à symétrie sphérique centré à
l’origine sur un objet S étendu dans le fond du ciel. Dans cet exemple, deux images de l’objet
sont vues par l’observateur O. Le panneau de droite montre une projection sur le plan x − y
(au z de la lentille) des deux images. L’image que l’on observerait en l’absence de lentille
est également montrée. À cause de la symétrie cylindrique, le mouvement des photons est
planaire et les deux images sont donc étirées dans la direction tangentielle. (Si l’objet était
directement derrière la lentille, l’image serait un cercle autour de l’origine.) À cause de cette
distorsion, les galaxies du fond du ciel peuvent apparaître sous la forme d’arcs comme on le
voit sur la ﬁgure 2.13.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
150
E
U
IQ
Chapitre 3. Coordonnées et métriques
T
Y
L
PO
N
H
EC
Finalement, notons qu’à cause de la distorsion de l’objet, la quantité totale de
lumière qui atteint l’observateur est modiﬁée. La ﬁgure 3.16 suggère que le ﬂux total
contenu dans une image donnée est proportionnel à la taille angulaire de l’image
puisque c’est cette taille qui détermine la taille du « trou » dans le plan de la lentille
au travers duquel les photons doivent passer sur leur chemin depuis la source jusqu’à
l’observateur. (Une démonstration plus rigoureuse de la proportionalité entre la taille
angulaire et le ﬂux devrait utiliser le théorème de Liouville.)
Le rapport entre le ﬂux total dans l’image i et le ﬂux qui atteindrait l’observateur
en absence de lentille est simplement
ÉC
E
L
O
bi dbi Ai =
.
b0 db0 (3.108)
E
U
IQ
Le premier facteur est dû à l’étirement dans la direction tangentielle et le second à
l’étirement dans la direction radiale.
Pour une lentille ponctuelle, il est assez simple de montrer que les deux ampliﬁcations 6 sont fonction du paramètre d’impact réduit u = b0 /RE
ÉC
E
L
O
T
Y
L
PO
A±
N
H
EC
√
u2 + 2 ± u u2 + 4
√
=
,
2u u2 + 4
(3.109)
où le « rayon d’Einstein » est donné par
2
=
RE
4GM Lx(1 − x)
,
c2
(3.110)
et où Lx est la distance entre observateur et lentille, L étant la distance observateursource. On voit que pour b0 RE , A+ = 1 et A− = 0 comme on s’y attend. Pour
b0 → 0 les ampliﬁcations deviennent formellement inﬁnies ce qui correspond à ce
qu’une source ponctuelle est déformée en un anneau. Cette divergence s’élimine si
l’on tient compte de la taille ﬁnie de la source, ce qui donne une extension eﬀective à
b0 .
Comme nous l’avons vu dans la section 4, l’eﬀet de lentille gravitationnelle a été
utilisé pour rechercher des objets sombres dans notre halo galactique. Dans ce cas,
les angles de déﬂexion sont tellement petits que les deux images ne sont pas résolues.
L’eﬀet n’est vu que par l’ampliﬁcation totale obtenue en sommant le ﬂux des deux
images (2.17). À cause du mouvement relatif transverse de la source, de la lentille et
de l’observateur, l’ampliﬁcation totale dépend alors du temps. La luminosité de l’objet
du fond croît puis retourne à sa valeur initiale ce qui donne la courbe de luminosité
de la ﬁgure 2.18.
6 Les
ÉC
E
L
O
Y
L
PO
puristes préfèrent utiliser le terme « magniﬁcation ».
H
C
TE
U
Q
I
N
E
Exercices sur le chapitre 3
Exercices
T
Y
L
PO
N
H
EC
E
U
IQ
151
3.1 Considérons un système de coordonnées lorentzien x̃ et un autre système de
coordonnées x déﬁni par
ÉC
E
L
O
xµ =
∂xµ α
x̃
∂ x̃α
x̃α =
∂ x̃α µ
x ,
∂xµ
(3.111)
où les coeﬃcients de transformation ∂ x̃α /∂xµ sont des constantes qui satisfont
ηαβ
∂ x̃α ∂ x̃β
= ηµν .
∂xµ ∂xν
(3.112)
(a) Montrer que les coordonnées x sont aussi lorentziennes :
dτ 2 = ηαβ dx̃α dx̃β = ηµν dxµ dxν .
N
H
EC
E
U
IQ
(3.113)
(b) Montrer que des rotations spatiales satisfont (3.112), par exemple
1
2
∂ x̃
∂ x̃
=
= cos θ
∂x1
∂x2
LY T
1
O
P
E
L
ÉCO
2
∂ x̃
∂ x̃
= − 1 = sin θ .
∂x2
∂x
(3.114)
(c) Montrer qu’une transformation de Lorentz propre (boost) satisfait (3.112), par
exemple
∂ x̃0
∂ x̃1
=
=γ
∂x0
∂x1
∂ x̃0
∂ x̃1
=
= βγ
∂x1
∂x0
(3.115)
où β = v/c et γ = (1 − β 2 )−1/2 .
3.2 En appliquant l’équation de la géodésique (3.79) à la métrique de Lorentz (3.14),
montrer que les particules suivent des chemins de vitesse constante.
3.3 Une fusée décolle verticalement de la Terre avec une vitesse inférieure à la vitesse
d’échappement (v c). Pendant son vol elle ne brûle pas de carburant. Après être
retombée à son point de départ on compare l’aﬃchage de l’horloge de la fusée avec
celui d’une horloge restée sur Terre.
(a) Laquelle des deux horloges a suivi une géodésique ? Quelle horloge a compté le
temps le plus court ?
(b) En négligeant la rotation de la Terre, intégrer le temps propre de la fusée donné
par (3.18) entre le décollage et le retour de la fusée sur Terre. Comparer le temps de
vol mesuré par l’horloge à bord avec celui mesuré par l’horloge restée au sol.
(c) Faire le même calcul pour un avion volant pendant un temps t à une altitude h
avant de revenir à sa base de départ.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
152
E
U
IQ
Chapitre 3. Coordonnées et métriques
T
Y
L
PO
N
H
EC
3.4 Monrer que l’équation de la géodésique (3.79) pour la métrique (3.18) est l’équation de Newton (3.19).
E
L
O
3.5 Considérons une sphère de rayon a. Un point sur la surface peut être repéré par
l’angle polaire χ et l’angle azimuthal θ. (Fig. 3.17).
(a) Montrer que la distance dS entre les points (χ, θ) et (χ + dχ, θ + dθ) est donnée
par
dS 2 = a2 dχ2 + sin2 χdθ2 ,
ÉC
qui peut être comparé à la métrique (3.50).
(b) Une autre coordonnée polaire r peut être déﬁnie par r = sin χ. Montrer que dS
est donné par
ï
ò
dr2
2
2
dS 2 = a2
+
r
dθ
,
1 − r2
N
H
EC
E
U
IQ
qui peut être comparé à la métrique (3.49).
(c) Considérons un objet de taille ∆S a au point (χ, θ). Supposons que cet objet
émet des photons qui sont astreints à se déplacer sur la surface de la sphère. Quelle
sera la taille angulaire de l’objet vu par un observateur au point χ = 0 ? Comment ce
résultat change-t-il si le rayon de la sphère est fonction du temps a(t) ? Comparer les
résultats avec (3.68).
(d) Calculer le nombre de photons observés, par unité de longueur et par unité de
temps, en χ = 0. Comparer les résultats avec (3.64).
ÉC
E
L
O
T
Y
L
PO
3.6 Considérons un espace euclidien à 4 dimesions avec des coordonnées x, y, z, w et
une métrique dS 2 = dx2 + dy 2 + dz 2 + dw2 . Une « 3-sphère » de rayon a peut être
déﬁnie par la contrainte x2 +y 2 +z 2 +w2 = a2 . Montrer que la distance dS entre points
voisins sur la surface de la 3-sphère est donné par la métrique de Robertson-Walker
avec k = 1, et x = ra sin θ cos φ, y = ra sin θ sin φ, et z = ra cos θ.
3.7 Considérons un univers k = 1. Expliquer pourquoi un objet à χ = π a une taille
angulaire (vue par un observateur à χ = 0) de ∆Ω = 4π, c’est-à-dire que l’objet
couvre tout le ciel.
H
C
TE
U
Q
I
N
3.8 Vériﬁer (3.61).
Comparer à l’ordre z 2 les quatre distances suivantes entre l’origine et χ1 :
– la distance de luminosité, dL ;
E
L
O
– la distance angulaire, dA ;
ÉC
Y
L
PO
– la « distance propre » , d1 = a1 χ1 , à t1 ;
E
Exercices sur le chapitre 3
ÉC
E
L
O
T
Y
L
PO
N
H
EC
χ
ÉC
E
L
O
T
Y
L
PO
E
U
IQ
N
H
EC
153
E
U
IQ
θ
U
Q
I
N
Fig. 3.17: Une sphère de rayon a. Un point de la surface peut être décrit par l’angle polaire
χ et l’angle azimuthal θ.
ÉC
E
L
O
Y
L
PO
H
C
TE
E
154
E
U
IQ
Chapitre 3. Coordonnées et métriques
T
Y
L
PO
– la « distance propre », d0 , à t0 .
N
H
EC
À partir de quelle distance les quatre distances commencent-elles à diﬀérer de ∼ 10% ?
E
L
O
3.9 Un explorateur quitte notre galaxie à t0 avec une vitesse v c après avoir
consommé tout son carburant.
(a) Calculer χ̇(t0 ), χ (t0 ), et t (t0 ).
(b) En utilisant (3.86) trouver une équation pour χ̇(t).
(c) Pour v = c/10, quel temps t est nécessaire au voyageur pour atteindre une galaxie
à z = 10−2 . (Le calcul peut être fait à l’ordre v/c.) Comparer le temps de voyage
mesuré par des horloges comobiles avec le temps mesuré par l’explorateur.
(d) Pour v c, quel est le redshift de la galaxie la plus lointaine que l’explorateur
peut visiter dans le cas a(t) ∝ t et a(t) ∝ t2/3 .
Cet exercice sera poursuivi dans l’exercice 5.14.
ÉC
N
H
EC
E
U
IQ
3.10 (Démonstration de (3.44).) En utilisant les transformations (3.41) et (3.43) montrer que
T
Y
L
PO
dx2 + dy 2 = sin2 θ dr2 + 2r sin θ cos θ drdθ
ÉC
E
L
O
+ r2 (sin2 θ dφ2 + cos2 θ dθ2 ) .
et qu’à l’ordre θ2
dz
2
Å
= dχ
2
θ2
rf (r)θ2
1−
+
f (r)
2f 2
ã
+
r2 θ2 dθ2
− −2rθ drdθ .
f (r)
En combinant ces deux résultats, montrer que
Å
ã
1
f (r)
− 1 + rθ2 dχ2
,
dx2 + dy 2 + dz 2 = dS 2 + r2 θ2 dθ2
f (r)
2f 2
où dS 2 est donné par (3.32) ou par (3.33). Les deux derniers termes dans le membre
de droite de cette équation sont d’ordre θ2 , si bien que nous pouvons utiliser les
approximations f (r) = f (r0 ), dχ = dz, et r2 θ2 dθ2 = (xdx + ydy)2 /r02 . Dans ces
approximations, montrer que la métrique spatiale est donnée par (3.44).
Y
L
PO
H
C
TE
U
Q
I
N
3.11 Avec f (r) donné par (3.47), la métrique (3.44) devient :
dS 2 = a2 [dz 2 (1 − bx2 − by 2 )
ÉC
E
L
O
+ dy 2 (1 + by 2 ) + dx2 (1 + bx2 ) + 2bxydxdy] .
(3.116)
E
Exercices sur le chapitre 3
T
Y
L
PO
N
H
EC
E
U
IQ
155
Cette métrique ne semble par décrire un espace isotrope autour du point (x = y =
z = 0) parce que les coordonnées x et y y ﬁgurent de façon diﬀérente de la coordonnée
z. Ce problème de cosmétique peut être remédié avec une transformation du troisième
degré :
ÉC
E
L
O
x = x + b(xy 2 + xz 2 + x3 )/4
y = y + b(yx2 + yz 2 + y 3 )4
z = z − b(x2 z + y 2 z − z 3 )/4 .
(3.117)
Avec cette transformation, montrer que la métrique devient (en laissant tomber les
primes)
dS 2 = a2 [dx2 + dy 2 + dz 2 ][1 − b(x2 + y 2 + z 2 )/2] .
N
H
EC
= a2 [dr2 + r2 (dθ2 + sin2 θ dφ2 ] [1 − r2 /2] .
T
Y
L
PO
E
U
IQ
(3.118)
où x = r sin θ cos φ, y = r sin θ sin φ, et z = r cos θ. Montrer qu’avec la transformation
r = r(1 − r2 /4), la métrique prend la forme :
(3.119)
dS 2 = a2 (1 + br2 )dr2 + r2 (dθ2 + sin2 θdφ2 ) .
ÉC
E
L
O
Cette métrique est identique à la métrique originale (3.33) à l’ordre r2 .
3.12 La ﬁgure 3.18 montre les trajectoires de deux two observateurs dans un espacetemps plat. L’observateur B est en récession par rapport à l’observateur A avec une
vitesse v = βc. A émet un photon à l’instant t1 mesuré par son horloge. Le photon est
réﬂéchi et retourne à t4 . A donne les coordonnées suivantes à l’événement réﬂexion :
x = (t4 − t1 )/2 .
t = (t4 + t1 )/2
(3.120)
Le photon passe chez l’observateur B à l’instant t2 puis à t3 . (Ces deux temps sont
mesurées par A avec son horloge et son radar.) D’après le postulat (3.5), le temps
mesuré par l’hologe de B lors de ces deux événements est
t3 = t3 1 − β 2 .
(3.121)
t2 = t2 1 − β 2
H
C
TE
B va attribuer à l’événement réﬂexion les coordonnées suivantes :
t = (t3 + t2 )/2
x = (t3 − t2 )/2 .
Y
L
PO
U
Q
I
N
(3.122)
(a) Montrer que (t , x ) est relié à (t, x) par une transformation de Lorentz :
Å ã
Å
ãÅ
ã
t
γ
−βγ
t
=
.
(3.123)
x
−βγ
γ
x
ÉC
E
L
O
E
156
ÉC
E
U
IQ
Chapitre 3. Coordonnées et métriques
T
Y
L
PO
E
L
O t A
N
H
EC
B
x=vt
t
4
t3
(t,x)
t
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
t2
t1
x
U
Q
I
N
Fig. 3.18: Trajectoires de deux observateurs, l’observateur A est à l’origine (x = 0) et
l’observateur B suit la trajectoire x = vt. A émet un photon à t1 (mesuré par l’horloge de
A). Le photon est réﬂéchi en (t, x) et retourne en A à t4 . A donne des coordonnées aux
événements distants en utilisant son horloge et son radar, c’est-à-dire t = (t4 + t1 )/2 et
x = (t4 − t1 )/2. B peut faire de même avec son horloge et son radar.
ÉC
E
L
O
Y
L
PO
H
C
TE
E
Exercices sur le chapitre 3
LY T
t
ÉC
E
L
O
PO
N
H
EC
E
U
IQ
157
B
A
x=vt
t=L/2
x=−L/2
x=L/2
x
T
Y
L
PO
t=−L/2
ÉC
E
L
O
N
H
EC
E
U
IQ
Fig. 3.19: Même ﬁgure que 3.18 sauf que A porte un barreau de longueur L dans la direction
du mouvement de B.
On voit qu’un seul observateur est nécessaire pour établir un système de coordonnées lorentziennes. Bien entendu, en échangeant des photons, l’observateur A peut
synchroniser son horloge avec d’autres hologes au repos (par rapport à A). Si l’on fait
cela, le temps de (t, x) dans le référentiel de A peut être mesuré localement.
(b) L’observateur A porte un barreau de longueur L orienté dans la direction du
mouvement de B. Utiliser la ﬁgure 3.19 pour montrer rapidement que B voit que le
barreau a subi une contratction de Lorentz d’un facteur 1/γ.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
ÉC
N
H
EC
T
Y
L
PO
E
L
O
E
U
IQ
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
E
T
Y
L
PO
N
H
EC
E
U
IQ
E
L
4
CO
ÉChapitre
Les équations du champ
gravitationnel
T
Y
L
PO
N
H
EC
E
U
IQ
L’évolution du paramètre d’échelle a(t) est régie par la gravitation au travers de
l’équation de Friedmann. Au chapitre 1, nous avons obtenu cette équation avec des
arguments newtoniens sujets à caution. Ici, nous allons redémontrer l’équation de
Friedmann dans le contexte de la théorie relativiste de la gravitation, c’est-à-dire la
relativité générale. Dans cette théorie, les paramètres de la métrique sont contraints
par l’équation des champs d’Einstein :
ÉC
E
L
O
Gµν = −8πGT µν .
(4.1)
Le membre de droite est proportionnel au tenseur d’énergie-impulsion qui est la source
de la gravitation. Le membre de gauche est le tenseur d’Einstein Gµν qui est fonction
des paramètres de la métrique. La composante 00 de l’équation des champs pour la
métrique de Robertson–Walker est appelée l’équation de Friedmann.
Nous verrons que la forme générale de Gµν est déterminée par la conservation
locale de l’énergie :
∂Gµν
∂T µν
=
0
⇒
= 0.
(4.2)
∂xµ
∂xµ
Cette forme de l’équation de conservation s’applique à l’origine d’un système de coordonnées localement lorentzien. L’équation de gauche dit simplement que la dérivée
temporelle de la densité d’énergie (densité d’impulsion) est donnée par la divergence
du ﬂux d’énergie (ﬂux d’impulsion). L’équation de droite découle de celle de gauche
et de l’équation des champs d’Einstein. Ce sera tout ce dont nous aurons besoin pour
ﬁxer la forme du tenseur d’Einstein et pour déduire les équations des champs de
Friedmann et d’Einstein.
Dans ce chapitre, il sera commode de choisir un système de coordonnées en chute
libre. Cela sera fait dans la section 1, où nous transformerons les coordonnées comobiles du chapitre 3 en coordonnées en chute libre avec la métrique qui, à des
ÉC
E
L
O
Y
L
PO
159
H
C
TE
U
Q
I
N
E
160
E
U
IQ
Chapitre 4. Les équations du champ gravitationnel
T
Y
L
PO
N
H
EC
corrections du second ordre près, est celle de la relativité restreinte. L’utilisation de
ces coordonnées nous permettra, dans la section 2, d’introduire le tenseur énergieimpulsion entièrement dans le cadre de la relativité restreinte. Après avoir trouvé
T µν , ce sera chose simple que de trouver l’équation de Friedmann à la section 3 en
imposant la conservation locale de l’énergie (4.2).
Bien que l’équation de Friedmann soit la seule nécessaire pour faire de la cosmologie homogène, pour d’autres applications, nous aurons besoin de la forme générale
de l’équation des champs d’Einstein. En ayant cela en tête, nous allons introduire le
tenseur de Riemann à la section 6. cela nous permettra de comprendre la signiﬁcation
physique des paramètres de la métrique puisque c’est ce tenseur qui régit le mouvement relatif physique de particules test, c’est-à-dire la déviation des géodésiques.
En imposant que le tenseur d’Einstein soit fonction du tenseur de Riemann avec
une quadri-divergence nulle, nous trouverons, à la section 8, l’équation des champs
applicable dans les systèmes en chute libre.
Enﬁn, dans la sectionb 9, nous ferons une transformation de coordonnées générale
qui nous donnera la forme compètement générale de l’équation des champs d’Einstein.
ÉC
1
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
Nos coordonnées en chute libre
En cosmologie, on utilise en général des coordonnées comobiles (t, χ, θ, φ) ou
(t, r, θ, φ) avec la métrique de Robertson–Walker :
ò
ï
dr2
2
2
2
2
+
r
(dθ
+
sin
θdφ
)
.
(4.3)
dτ 2 = dt2 − a(t)2
1 − kr2
ÉC
E
L
O
Malgré l’utilité des coordonnées comobiles, la dynamique de l’univers, c’est-à-dire
la dépendance en temps de a(t), peut se comprendre plus facilement si l’on choisit
un ensemble de coordonnées en chute libre1 (x̃µ , µ = 0, 1, 2, 3) avec une métrique
localement lorentzienne près de l’origine x̃µ = 0 :
gµν = ηµν +
1
gµν,αβ (0)x̃α x̃β + ..... .
2
(4.4)
Ici, ηµν est la métrique d’un espace-temps plat :
η00 = −η11 = −η22 = −η33 = 1
ηµ=ν = 0 ,
et
gµν,αβ ≡
∂ 2 gµν
.
∂ x̃α ∂ x̃β
Y
L
PO
H
C
TE
(4.5)
U
Q
I
N
(4.6)
La métrique (4.4) est localement lorentzienne car les corrections à ηµν sont quadratiques dans les coordonnées x̃µ . La métrique de Robertson–Walker (4.3) n’est pas
localement lorentzienne car ȧ = 0.
E
L
O
1 Dans un contexte cosmologique, « en chute libre » est peut être mal choisi puisque dans un
univers homogène il n’y a pas de direction dans laquelle tomber.
ÉC
E
Nos coordonnées en chute libre
T
Y
L
PO
N
H
EC
E
U
IQ
161
Une méthode générale pour construire des coordonnées en chute libre est d’équiper
un observateur en chute libre avec une horloge et un radar. L’observateur peut alors
utiliser son équipement de la façon habituelle pour mesurer les temps et les distances.
Il se trouve que cela donne automatiquement des coordonnées avec une métrique qui
est localement lorentzienne. L’observateur que nous utiliserons est celui à l’origine du
système de coordonnées comobile, c’est-à-dire nous-mêmes.
La situation est illustrée sur la ﬁgure 4.1. L’observateur à l’origine (χ = 0) tente
de mesurer le temps et la position d’un événement de coordonnées comobiles (t, χ). A
t = ta l’observateur émet un photon qui est réﬂéchi à (t, χ) et revient à l’origine à t =
tb . Il est normal pour l’observateur d’attribuer les coordonnées (T, R) à l’événement
avec
tb + t a
− t0
T =
(4.7)
2
ÉC
E
L
O
tb − t a
.
2
R =
N
H
EC
E
U
IQ
(4.8)
La relation entre les coordonnées (T, R) et (t, r) est simple à trouver parce que la
trajectoire du photon entre ta et t est gouvernée par
t
t
dt
dt
χ =
=
,
(4.9)
ta a(t )
ta a(t)[1 + H(t)(t − t) + .....]
E
L
O
et, entre t et tb , par
ÉC
tb
χ =
t
T
Y
L
PO
dt
=
a(t )
t
tb
dt
.
a(t)[1 + H(t)(t − t) + .....]
(4.10)
En prenant la somme et la diﬀérence de ces deux équations on trouve (exercice 4.1)
T = t − t0 + a(t)ȧ(t)r2 /2 + O(r3 )
(4.11)
R = a(t)r + O(r3 ) .
(4.12)
Pour trouver la métrique dans le système (T, R), on a besoin des transformations
inverses t(T, R) et r(T, R). En substituant (4.12) dans (4.11) on obtient
t = t0 + T − (1/2) R2
R
.
a(t)
ȧ
a
Y
L
PO
r =
H
C
TE
U
Q
I
N
(4.13)
(4.14)
Pour éliminer la dépendance en t de a(t) dans ces deux équations, nous développons
a(t) en série de Taylor (2.5) :
ÉC
E
L
O
a(t) = a0 [1 + H0 (t − t0 ) − (1/2)q0 H02 (t − t0 )2 ] ,
E
162
ÉC
E
U
IQ
Chapitre 4. Les équations du champ gravitationnel
E
L
O
T
Y
L
PO
N
H
EC
t
tb
T
Y
L
PO
(t, χ)
ÉC
E
L
O
N
H
EC
E
U
IQ
ta
t0
χ=0
χ
Fig. 4.1: Construction de coordonnées en chute libre par un observateur à l’origine équipé
d’une horloge et d’un radar. L’observateur émet un photon à t = ta qui est réﬂéchi au point
de coordonnées comobiles (t, χ). Le photon revient à l’origine à t = tb . L’observateur peut
associer à l’événement (t, χ) une coordonnée radiale R = (tb − ta )/2 et une coordonnée
temporelle T = (tb + ta )/2 − t0 . La métrique du système (T, R) est localement lorentzienne
à l’origine.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Nos coordonnées en chute libre
T
Y
L
PO
ce qui implique
N
H
EC
E
U
IQ
163
ȧ
= H0 [1 − (1 + q0 ) H0 (t − t0 ) ] .
a
E
L
O
En substituant ceci dans (4.13) et (4.14) on trouve
ÉC
t = t0 + T − (1/2) R2 H0 [1 − (1 + q0 ) H0 (t − t0 ) ]
r =
R
[1 − H0 (t − t0 ) + (1 + q0 /2) H02 (t − t0 )2 ] .
a0
Puisque nous travaillons à l’ordre R2 et T 2 , on peut utiliser t − t0 ∼ T − (1/2)R2 H0
pour trouver les transformations ﬁnales t(T, R) et r(T, R) :
t = t0 + T − (1/2) R2 H0 [1 − (1 + q0 ) H0 T ] + .....
r =
N
H
EC
E
U
IQ
R
[1 − H0 (T − R2 H0 /2) + (1 + q0 /2) H02 T 2 ] + ..... .
a0
T
Y
L
PO
(4.15)
(4.16)
En substituant (4.15) et (4.16) dans la métrique de Robertson–Walker , on obtient
la métrique dans le système (T, R) à l’ordre R2 :
dτ 2 = dT 2 1 − αR2
ÉC
E
L
O
− dR2
1 + βR2
− R2 dθ2 + sin2 θ dφ2 ,
(4.17)
où les coeﬃcients α et β sont
α =
ï ò
ä
≡ −H02 q0
a t0
ô
ñÅ ã2
k
k
ȧ
β =
+ 2
= H02 + 2 .
a
a t
a0
(4.18)
0
U
Q
I
N
En appliquant les transformations standard X = R sin θ cos φ, Y = R sin θ sin φ et
Z = R cos θ la métrique prend une forme localement lorentzienne :
dτ 2 = dT 2 − dX 2 − dY 2 − dZ 2
H
C
TE
2
−αdT X 2 + Y 2 + Z 2 − β (XdX + Y dY + ZdZ) .
2
Y
L
PO
(4.19)
Bien que cette métrique soit localement lorentzienne, il est utile de faire une transformation de plus :
ÉC
E
L
O
x̃1 = X(1 − βR2 /4)
E
164
E
U
IQ
Chapitre 4. Les équations du champ gravitationnel
N
H
EC
x̃2 = Y (1 − βR2 /4)
ÉC
E
L
O
T
Y
L
PO
x̃3 = Z(1 − βR2 /4)
(4.20)
x̃0 = T .
(4.21)
Cette transformation donne une métrique qui est localement lorentzienne et « orthogonale » (gµ=ν = 0) :
dτ 2 = dx̃0 dx̃0 1 − αR2
ï
ò
1
− dx̃1 dx̃1 + dx̃2 dx̃2 + dx̃3 dx̃3 1 − βR2 ,
2
c’est-à-dire
g00 = 1 − αR2
N
H
EC
E
U
IQ
gii = −(1 − βR2 /2) i = 1, 2, 3 ,
T
Y
L
PO
(4.22)
(4.23)
avec R2 = x̃1 x̃1 + x̃2 x̃2 + x̃3 x̃3 .
Les coordonnées x̃ déﬁnissent le système en chute libre que nous utiliserons dans
l’essentiel de ce chapitre. Ce n’est manifestement pas le seul système de ce genre.
A côté des transformations du troisième ordre comme (4.20), les transformations de
Lorentz et les rotations spatiales (exercice 3.1) appliquées aux coordonnées x̃ donnent
également des coordonnées avec une métrique localement lorentzienne. Toutefois, x̃
est particulier car il est centré sur un observateur comobile (nous). L’univers doit
donc être isotrope dans le système x̃. A cause de cela, le tenseur énergie-impulsion et
les équations des champs d’Einstein prennent des formes simples, comme nous allons
le voir dans les sections suivantes.
ÉC
2
E
L
O
Le tenseur énergie-impulsion
Dans cette section, nous allons trouver la « source » de la gravitation, le tenseur
énergie-impulsion, T µν . L’équation des champs d’Einstein est une équation locale et
nous pouvons donc considérer une petite région spatiale autour de l’origine. Nous
pouvons utiliser les coordonnées en chute libre trouvées ci-dessus. Ces coordonnées
ont une métrique d’espace-temps plat à des corrections quadratiques dans la distance
à l’origine. Il se trouve que nous n’aurons besoin de T µν qu’à des corrections linéaires
près et notre discussion de T µν va se faire entièrement dans le cadre de la relativité
restreinte.
Nous cherchons la généralisation relativiste de l’équation de Poisson pour le potentiel gravitationnel Φ :
ÉC
E
L
O
Y
L
PO
∇2 Φ = 4πGρ ,
H
C
TE
U
Q
I
N
(4.24)
E
Le tenseur énergie-impulsion
T
Y
L
PO
N
H
EC
E
U
IQ
165
où la source de la gravitation dans le menbre de droite est la densité de masse (ou
d’énergie) ρ. Pour trouver la généralisation relativiste de ρ, nous pouvons nous laisser
guider par la généralisation de l’équation de Poisson pour le potentiel électrostatique
Φq :
ã
Å 2
∂
2
Aµ = 4πj µ .
∇2 Φq = −4πρq
→
−
∇
(4.25)
∂t2
ÉC
E
L
O
Dans la généralisation relativiste, nous avons remplacé le potentiel par le quadrivecteur potentiel Aµ et ∇2 par l’opérateur invariant (∂ 2 /∂t2 − ∇2 ). Le remplacement
de la densité de charge par le quadrivecteur courant j µ se justiﬁe aisément. Considérons un ensemble de particules de charge q toutes au repos. La densité de charge est
ρq = qn où n est le nombre volumique de particules. Si nous supposons que ρq est la
composante 0 d’un quadrivecteur, une transformation de Lorentz donne
ã
Å ã
Å
ãÅ
ã
Å
ã
Å
ρ
γ βγ
qn
qγn
qn
=
,
(4.26)
=
=
qβn
jx
βγ γ
0
qβγn
N
H
EC
E
U
IQ
où le nombre volumique dans le référentiel « primé » est n = γn à cause de la
contraction de Lorentz. On voit que dans le référentiel primé, la composante 0 est
toujours la densité de charge, ce qui conﬁrme que ρq est, eﬀectivement, la composante
0 d’un quadrivecteur.
Il est tentant d’essayer de faire la même chose pour la gravitation. Cependant,
si l’on suppose que la densité d’énergie est la composante 0 d’un quadrivecteur, une
transformation de Lorentz va nous donner un quadrivecteur dont la composante 0
n’est plus la densité d’énergie. Cela provient de ce que la transformation de Lorentz
modiﬁe par un facteur γ à la fois le nombre volumique des particules et leur énergie.
Une deuxième possibilité est de supposer que la densité d’énergie est la composante
00 d’un tenseur. Dans ce cas, une transformation de Lorentz nous rend un objet dont
la composante 00 est toujours la densité d’énergie :
ã
Å
ãÅ
ãÅ
ã
Å
γ βγ
mn 0
γ βγ
(γm)(γn)
(βγm)(γn)
=
2
βγ γ
0 0
βγ γ
(βγm)(γn) (β γm)(γn)
ÉC
E
L
O
T
Y
L
PO
Å
=
E
px
ã
px
(px px /E )
n .
U
Q
I
N
(4.27)
H
C
TE
On peut donc choisir la densité d’énergie ρ comme étant la composante 00 d’un tenseur
T µν .
Les autres composantes de T µν sont peut-être encore un peu obscures. Eﬀectuons
une rotation autour de l’axe z :
Ö
èÖ
èÖ
è
1
0
0
0
0
cos θ
sin θ
0
0
− sin θ
cos θ
0
ÉC
0
0
0
1
E
px
0
0
E
L
O
Y
L
PO
px
px px /E
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
cos θ
− sin θ
0
0
sin θ
cos θ
0
0
0
0
1
E
166
E
U
IQ
Chapitre 4. Les équations du champ gravitationnel
Ü
T
Y
L
PO
=
E
L
O
N
H
EC
E
px
py
0
py
px py /E
py py /E
0
px
px px /E
py px /E
0
0
0
0
0
ê
.
(4.28)
A ce point, le lecteur est certainement convaincu que les composantes générales
de T µν pour un ensemble de particules monocinétiques sont
ÉC
T µν = n(x̃)
pµ pν
.
E
(4.29)
Le comportement de cet objet par transformation de Lorentz et par rotations spatiales
est entièrement déterminé par la quantité pµ pν puisque n/E est invariant.
Puisque la somme de deux tenseurs est un tenseur, pour un ensemble polycinétique
de particules, l’énergie-impulsion se calcule en intégrant (4.29) sur l’impulsion :
3
≠ µ ν∑
d p
p p
µν
µ ν
F (p, x̃) p p = n(x̃)
,
(4.30)
T
=
E
E
N
H
EC
E
U
IQ
où F (p, x̃) = dN/d3 p d3 x est la densité de particules dans l’espace des phases et n(x̃)
est la densité de particules dans l’espace. On voit que la composante 00 est la densité
d’énergie, T 00 = ρ = nE, comme on s’y attendait.
Nous voulons laisser ouverte la possibilité d’une densité d’énergie qui ne soit pas
associée à la présence de particules. Nous appellerons cette densité d’énergie la densité
d’énergie du vide ρV :
ÉC
E
L
O
T
Y
L
PO
T 00 = ρV + n(x̃) E .
(4.31)
En l’absence de particules ou de champs classiques, tous les référentiels de Lorentz
devraient être équivalents et il est normal de supposer que ρV est un invariant de
Lorentz. Cette condition détermine la forme du tenseur énergie-impulsion du vide
puisque, comme nous le montrons dans l’appendice A, le seul tenseur invariant de
Lorentz est η µν = ηµν :
TΛµν = ρV η µν .
(4.32)
Le dernier type de tenseur d’énergie-impulsion intéressant pour la cosmologie est
le tenseur associé aux champs macroscopiques. Nous considérerons ce cas dans la
section 5.
Nous allons maintenant calculer T µν dans notre système de coordonnées en chute
libre x̃. Pour l’équation des champs d’Einstein à l’origine, nous avons seulement besoin
de T µν à l’origine. En ce point, la vitesse de Hubble est nulle et les galaxies (ou
particules) dans une petite boîte auront une distribution en impulsion isotrope, c’està-dire une distribution dominée par les vitesses particulières. Il s’ensuit qu’à l’origine
pi = pi pj=i = 0 et les éléments non-diagonaux de T µν s’annulent à l’origine.
ÉC
E
L
O
Y
L
PO
H
C
TE
T µ=ν (x̃1 = x̃2 = x̃3 = 0) = 0 .
U
Q
I
N
(4.33)
E
Le tenseur énergie-impulsion
T
Y
L
PO
La composante 00 est, comme toujours,
N
H
EC
E
U
IQ
T 00 (x̃1 = x̃2 = x̃3 = 0) = ρ ,
E
L
O
167
(4.34)
où ρ est la densité d’énergie. Les composantes espace-espace à l’origine sont
ÉC
T 11 (0) = T 22 (0) = T 33 (0) = n(x̃)|p|2 /3E ≡ p ,
(4.35)
où cette équation déﬁnit la « pression » p. On peut montrer (exercice 4.3) que cette
déﬁnition de la pression est en accord avec la déﬁnition habituelle pour un gaz parfait
à la température T aussi bien dans la limite non-relativiste (T m) que relativiste
(T m). Toutefois, il est important de se souvenir que dans le contexte présent,
T ii a le rôle d’une source de gravité. En raison de notre association intuitive de la
« pression » comme une force par unité d’aire, il est peut-être préférable d’appeler p
la « densité » de |p|2 /3E”.
Notons que la déﬁnition (4.30) implique les relations suivantes entre densité d’énergie et pression (« équations d’état ») :
|p| ρ
T
Y
L
PO
p = ρ/3
E
L
O
N
H
EC
particules non − relativistes
particules relativistes
E
U
IQ
.
(4.36)
(4.37)
L’équation (4.32) donne une valeur curieuse de la pression du vide :
ÉC
p = −ρ
vide .
(4.38)
La pression du vide est négative si la densité d’énergie du vide est positive. Une
pression négative peut paraître étrange mais c’est le prix à payer pour avoir une
densité d’énergie invariante de Lorentz.
Avant d’écrire les équations des champs, il est utile d’étudier la conservation locale de l’énergie (4.2). Pour un système de particules avec T µν donné par (4.30), la
composante 0 de (4.2) est
∂ρ
· jE = 0 ,
+ ∇
∂t
(4.39)
où le « courant d’énergie » a la forme attendue
jE = nEv v =
p
.
E
T
Y
POL
H
C
E
U
Q
I
N
(4.40)
L’équation (4.39) est l’analogue pour l’énergie de l’équation locale de conservation de
jq = 0 avec le courant de charge habituel donné par jq = qnv .
la charge ∂ρq /∂t + ∇·
Pour appliquer la conservation locale de l’énergie (4.2) à notre système x̃, nous
avons besoin de T µν au point (dx̃1 , dx̃2 , dx̃3 ) = (0, 0, 0). La façon la plus simple de
calculer T µν hors de l’origine est de prendre le T µν vu par un observateur comobile et
ÉC
E
L
O
E
168
E
U
IQ
Chapitre 4. Les équations du champ gravitationnel
N
H
EC
d’en faire la transformation de Lorentz avec β = RH0 = R/dH 1. A l’ordre R/dH
on trouve :
Å
ãÅ
ãÅ
ã
Å
ã
γ βγ
ρ 0
γ βγ
ρ
β(ρ + p)
=
,
(4.41)
βγ γ
0 p
βγ γ
β(ρ + p)
p
ÉC
E
L
O
T
Y
L
PO
c’est-à-dire
T 00 (x̃) = ρ
(4.42)
T ij (x̃) = p δi,j
i, j = 1, 2, 3
T i0 (x̃) = (ρ + p) H0 x̃i
i = 1, 2, 3 .
N
H
EC
(4.43)
E
U
IQ
(4.44)
Il est important d’insister sur le fait que ρ et p sont la densité d’énergie et la pression mesurées localement par un observateur comobile, c’est-à-dire un observateur
comobile utilisant son référentiel de Lorentz local.
Notons que T i0 (x̃) a la forme attendue pour un courant d’énergie, c’est-à-dire la
densité de masse multipliée par la vitesse de Hubble dans le cas où p = 0. Notons
également que le courant d’énergie du vide s’annule. On doit s’y attendre puisque le
vide ne contient pas de particules en mouvement.
En prenant la quadri-divergence de T µν donné par (4.42), (4.43) et (4.44) nous
trouvons l’équation de conservation locale de l’énergie :
ÉC
E
L
O
T
Y
L
PO
ȧ
∂ρ
= −3 (ρ + p) ,
∂t
a
(4.45)
où nous avons fait usage de ce que x̃0 = T = t à l’origine. Les solutions de cette
équation pour l’énergie de la matière, du rayonnement et du vide sont :
ρM (a) = ρM (a0 )â−3
|p| ρ
ρR (a) = ρR (a0 )â−4
matière non − relativiste
p = ρ/3
ρV (a) = ρV (a0 )
(4.46)
matière relativiste
(4.47)
H
C
TE
(4.48)
p = −ρ
vide .
U
Q
I
N
ces solutions conﬁrment les dépendances en a trouvées au chapitre 1. Encore une fois,
le fait que la densité d’énergie du vide soit une constante est du à ce que sa valeur
est indépendante du nombre de particules en présence. A cause de leur mouvement
aléatoire, les particules (galaxies) massives vont quitter la région autour de l’origine.
Elles ne sont pas remplacées par d’autres particules à cause de la vitesse de Hubble
des particules lointaines. Il ne reste que le vide !
ÉC
E
L
O
Y
L
PO
E
L’équation de Friedmann
T
Y
L
PO
L’équation (4.45) équivaut à
E
L
O
N
H
EC
E
U
IQ
d(ρa3 )
= −p .
da3
169
(4.49)
qui équivaut, à son tour, au premier principe de la thermodynamique pour une expansion adiabatique :
ÉC
d(ρa3 ) = −pda3
⇒
dE = −pdV ,
(4.50)
où E est l’énergie contenue dans un volume ﬁxe comobile, c’est-à-dire un volume borné
par des coordonnées comobiles ﬁxes. Nous utiliserons cette relation au chapitre 6 en
étudiant la thermodynamique de l’univers.
Terminons par une remarque sur la conservation de l’énergie en cosmologie. La
conservation de l’énergie locale s’exprime par (4.39) et (4.45). La conservation de
l’énergie globale s’obtient si nous pouvons appliquer le théorème de Gauss à (4.39) en
intégrant sur quelque volume ﬁni V qui contient toute l’énergie :
∂ρ
dE
(4.51)
=
dV
=
dS n̂ · jE ,
dt
∂t
T
Y
L
PO
N
H
EC
E
U
IQ
où la première intégrale porte sur le volume et la seconde sur la frontière de ce volume.
L’énergie totale n’est conservée que s’il y a une surface sur laquelle le courant d’énergie
s’annule. Il y a deux raisons pour lesquelles ce n’est pas le cas en cosmologie. La
première est que si l’univers est homogène il n’y a pas de surface où le courant s’annule.
La seconde est que (4.39) ne s’applique que dans des coordonnées de Lorentz. Puisqu’il
n’est pas possible de déﬁnir des coordonnées globalement lorentziennes en présence de
la gravité, et que l’on ne peut déﬁnir que des coordonnées localement lorentziennes,
on ne peut pas appliquer (4.39) même si l’énergie est concentrée dans un volume ﬁni.
Il y a, bien sûr, des quantités qui sont approximativement conservées en cosmologie. Pendant l’époque du rayonnement, ρa4 est conservé, et pendant l’époque
de matière c’est ρa3 qui est conservé. Cette dernière quantité a la dimension d’une
énergie et mène par conséquent à une certaine confusion parce que cela pousse à l’interpréter comme l’énergie totale de l’univers, même si le volume l’univers est inﬁni.
L’équation de Friedmann implique que la quantité ȧ2 − 8πGρa2 /3 est indépendante
du temps. Nous avons interprété cela dans la section 2.2 comme la conservation de
l’énergie totale d’une seule particule proche comobile.
ÉC
3
E
L
O
L’équation de Friedmann
Y
L
PO
H
C
TE
U
Q
I
N
La forme du tenseur d’Einstein Gµν va être déterminée par la conservation de
l’énergie (4.2) qui implique que la quadri-divergence de Gµν s’annule. Il n’est donc pas
étonnant que nous puissions trouver directement l’équation de Friedmann en imposant
la conservation locale de l’énergie sans nous préoccuper de la forme générale de Gµν .
Pour le faire, nous allons supposer que dans l’équation des champs pour un univers
ÉC
E
L
O
E
170
E
U
IQ
Chapitre 4. Les équations du champ gravitationnel
N
H
EC
homogène, les composantes de T µν sont des fonctions linéraires des paramètres de la
métrique (4.23), α = ä/a et β = (ȧ/a)2 + k/a2 :
ÉC
E
L
O
T
Y
L
PO
GT 00 = Gρ = Aα + Bβ
(4.52)
GT ii = Gp = Cα + Dβ ,
(4.53)
où A, B, C et D sont des constantes qui, par analyse dimensionnelle, sont des nombres
purs. En utilisant (4.53) pour éliminer α dans (4.52) et en diﬀérenciant, nous trouvons
ρ̇ = (A/C)ṗ + β̇ (BC − AD)/GC
= (A/C)ṗ + 2(ȧ/a)(α − β) (BC − AD)/GC
HN
2
ȧ
A
ṗ −
[(D + C)ρ − (B + A)p] .
=
C
C
a
C
E
T
LY
E
U
IQ
(4.54)
En comparant la dernière forme avec (4.45), on voit que l’on doit imposer A = 0 si
l’on veut satisfaire (4.45) pour toutes les relations possibles entre ρ et p. En égalant
les coeﬃcients de ρ et p, nous trouvons C = −2B/3 et D = −B/3 :
ñÅ ã2
ô
ȧ
k
Gρ = B
(4.55)
+ 2 ,
a
a
et
O
P
E
L
ÉCO
B
Gp = −
3
ñ
2ä
+
a
ô
Å ã2
ȧ
k
+ 2 .
a
a
(4.56)
L’équation des champs d’Einstein et sa limite newtonienne (exercice 4.6) vont nous
donner la valeur de la constante B = 3/8π. Les équations (4.55) et (4.56) deviennent
alors les équations des champs pour un univers homogène :
Å ã2
ȧ
k
8πGρ
+ 2 =
a
a
3
−2ä
−
a
(équation de Friedmann)
H
C
TE
Å ã2
ȧ
k
− 2 = 8πGp .
a
a
Y
L
PO
U
Q
I
N
(4.57)
(4.58)
Résumons les hypothèses nécessaires pour faire cette rapide démonstration de
l’équation de Friedmann (4.57) :
E
L
O
– L’univers est homogène, ce qui implique que l’on peut trouver un système de
coordonnées avec la métrique de Robertson–Walker (4.3).
ÉC
E
Les paramètres cosmologiques
T
Y
L
PO
N
H
EC
E
U
IQ
171
– Le tenseur énergie-impulsion est une fonction linéaire des coeﬃcients des termes
quadratiques dans la métrique localement lorentzienne (4.23) déduite de la métrique de Robertson–Walker, c’est-à-dire ä/a et (ȧ/a)2 + k/a2 .
E
L
O
– L’énergie est conservée localement (4.45).
La démonstration générale de l’équation des champs d’Einstein élimine la première
hypothèse, ce qui nous permet de traiter les conﬁgurations énergétiques générales.
On peut combiner les composantes spatiales et la composante 00 de l’équation des
champs (4.57) et (4.58) pour trouver une équation pour la décélération de l’univers :
ÉC
−4πG
ä
=
(ρ + 3p) .
a
3
(4.59)
Cette équation résume la physique gravitationnelle qui détermine l’expansion. Si
l’univers est dominé par de la matière non-relativiste, (p ρ), l’univers est décéléré
par la gravitation ä/a = −4πGρ/3, en accord avec le calcul newtonien du chapitre 1.
Dans ce cas, le terme 3p donne une petite correction « relativiste ». Pour un univers
dominé par de la matière relativiste, (p = ρ/3), la décélération est le double de la
valeur non-relativiste. Pour un univers dominé par l’énergie du vide, (p = −ρ), la
décélération est négative, c’est-à-dire que l’expansion est accélérée.
N
H
EC
4
E
U
IQ
T
Y
L
Les paramètres P
cosmologiques
O
E
L
ÉCO
Il est utile de mettre l’équation de Friedmann sous une forme qui contient les
valeurs actuelles du taux d’expansion et des paramètres de densité. A t = t0 (4.57)
prend la forme
k
8πGρ(t0 )
− H02 = H02 (ΩT − 1) .
=
2
a0
3
(4.60)
On voit que le signe de k est déterminé par ΩT :
ΩT
> 1
= 1
< 1
k=
+1
0 .
−1
(4.61)
L’équation (4.60) nous donne la valeur de a0 :
H0−1
dH
= .
a0 = |ΩT − 1|
|ΩT − 1|
T
Y
POL
H
C
E
U
Q
I
N
(4.62)
Sauf si ΩT est très proche de un, a0 est de l’ordre de la distance de Hubble dH =
cH0−1 . Rappelons que a0 donne l’échelle de distance à laquelle les violations de la
géométrie euclidienne deviennent grandes, par exemple ∆Θ = ∆S/R. Le fait que a0
diverge pour ΩT = 1 n’est par conséquent pas surprenant puisque dans ce cas, la
relation euclidienne est exacte. Comme nous le verrons, la divergence de a0 ne cause
ÉC
E
L
O
E
172
E
U
IQ
Chapitre 4. Les équations du champ gravitationnel
T
Y
L
PO
N
H
EC
aucun problème pratique dans le calcul de distances angulaires ou de luminosité car
la quantité a0 χ est toujours régulière.
Le paramètre de courbure k peut maintenant être éliminé de l’équation de Friedmann en substituant (4.60) dans (4.57) :
Å ã2
ȧ
8πGρ
+ H02 (1 − ΩT ) â−2
=
a
3
ÉC
E
L
O
ï
=
H02
ò
ρ(a)
−2
+ (1 − ΩT ) â
.
3H02 /8πG
(4.63)
Pour trouver la solution de l’équation de Friedmann, nous avons besoin de la
densité d’énergie en fonction du paramètre d’échelle. Pour la matière non-relativiste,
le rayonnement et l’énergie du vide, nous avons trouvé les résultats (4.46), (4.47) et
(4.48). Pour un mélange de ces trois types d’énergie, l’équation de Friedmann est donc
Å ã2
ȧ
= H02 ΩM â−3 + ΩR â−4 + ΩΛ + (1 − ΩT ) â−2 ,
(4.64)
a
T
Y
L
PO
N
H
EC
E
U
IQ
où les Ω réfèrent tous aux valeurs actuelles des densités :
Ωi =
et où
ÉC
E
L
O
ρi (a0 )
3H02 /8πG
i = M, R, Λ ,
ΩT = ΩM + ΩR + ΩΛ .
(4.65)
(4.66)
La forme (4.64) de l’équation de Friedmann est correcte seulement si toute l’énergie
est soit relativiste, soit non-relativiste, soit de l’énergie du vide. Il y a deux situations
où cela n’est pas le cas. La première se présente lorsque la température est de l’ordre
de la masse d’une des espèces de particules en présence. Dans ce cas, les particules ne
sont ni relativistes ni non-relativistes. La technique pour traiter ce cas sera présentée
au chapitre 6. La seconde se présente lorsqu’il existe une énergie associée avec un
champ classique, comme dans l’époque inﬂationnaire. Ce cas sera traité dans la section
suivante.
Le paramètre de décélération est donné par (4.59) à t0 :
ï ò
ΩM
ä
− ΩΛ .
q0 ≡ −H0−2
=
(4.67)
a t0
2
H
C
TE
U
Q
I
N
Comme nous l’avons déjà fait remarquer, une énergie du vide positive accélère l’expansion.
Finalement, dans les conditions d’aujourd’hui (4.60) et (4.67), la métrique du
système en chute libre (4.17) et (4.18) prend la forme
Ç
Å
ã å
R 2
dτ 2 = dT 2 1 + (ΩM /2 − ΩΛ )
dH
ÉC
E
L
O
Y
L
PO
E
Champs scalaires
Ç
− dR
2
Å
O
P
E
L
ÉCO
N
H
EC
ã2 å
LY T
1 + ΩT
R
dH
− R
2
E
U
IQ
2
dθ + sin2 θ dφ2 .
173
(4.68)
On voit que pour des distances R dH , la métrique est bien approchée par la métrique de Lorentz. Cela justiﬁe que nous ignorions la gravité pour des eﬀets purement
locaux comme nous l’avons fait dans la section 2 lorsque nous avons calculé l’évolution
de la température du CBR.
5
Champs scalaires
Pendant les deux dernières décennies, les champ scalaires macroscopiques sont devenus des objets importants dans la cosmologie spéculative. Pour l’univers primordial,
les champs scalaires sont supposés dominer l’univers pendant l’époque inﬂationnaire.
Dans l’univers actuel, ils sont utilisés dans les modèles de « quintessence » pour
fournir l’équivalent dynamique d’une constante cosmologique. On préfère les champs
scalaires par rapport, par exemple, aux champs vectoriels car ils ne donnent pas de
direction spatiale privilégiée, ce qui pourrait mener à une violation de l’invariance de
Lorentz.
Comme avec les particules et l’énergie du vide, nous allons traiter les champs
scalaires dans un système en chute libre dans le cadre de la relativité restreinte.
Nous considérons donc un champ hypothétique φ(x̃) invariant par transformation de
Lorentz. Une équation invariante relativiste pour φ est
ÉC
E
L
O
η µν
T
Y
L
PO
N
H
EC
E
U
IQ
∂2φ
∂2φ
+ V (φ) =
− ∇2 φ + V (φ) = 0 ,
µ
ν
∂ x̃ ∂ x̃
∂T 2
(4.69)
où η µν = ηµν , et où V (φ) est « l’énergie potentielle » du champ. Pour V (φ) =
m2 φ2 /2, (4.69) est l’équation de Klein–Gordon bien connue. Puisque nous n’avons
pas de contraintes de la part de la physique fondamentale, le potentiel des modèles
d’inﬂation ou de quintessence peuvent être choisis pour résoudre certains problèmes
cosmologiques.
Le tenseur énergie-impulsion pour un champ scalaire est
T µν = η µα η νβ Tαβ
avec
Tµν =
∂φ ∂φ
1
− ηµν
∂ x̃µ ∂ x̃ν
2
ñÅ
∂φ
∂T
ô
ã2
H
C
E
· ∇φ
− 2 V (φ)
− ∇φ
T
Y
POL
.
U
Q
I
N
(4.70)
La justiﬁcation de l’utilisation de cette forme pour Tµν tient dans seul le fait que sa
quadri-divergence s’annule :
ÉC
E
L
O
∂T µν
= 0,
∂ x̃µ
(4.71)
E
174
E
U
IQ
Chapitre 4. Les équations du champ gravitationnel
T
Y
L
PO
N
H
EC
comme on le vériﬁe immédiatement en utilisant (4.69).
Dans les cosmologies inﬂationnaires ou quintessentielles, on est souvent intéressé
par des potentiels non-nuls et relativement plats, V (φ) = 0 et V (φ) ∼ 0. Dans ce cas,
une solution de (4.69) est :
ÉC
E
L
O
φ ∼ constante.
(4.72)
En ignorant toutes les dérivées dans Tµν on trouve
T00 = ρ ∼ V (φ)
(4.73)
Txx = Tyy = Tzz = p ∼ −V (φ) .
(4.74)
Nous voyons que dans ce cas le tenseur énergie-impulsion est approximativement celui
du vide. C’est cette caractéristique qui est exploitée dans les modèles inﬂationnaires
ou quintessentiels.
Il sera utile de trouver la forme de (4.69) dans des coordonnées comobiles (t, r).
Considérons un champ φ(R, T ) = φ(r, t). Nous nous intéresserons surtout au cas où
φ est spatialemnt homogène dans des coordonnées comobiles :
∂φ
= 0.
(4.75)
∂r
En utilisant les transformations (4.15) et (4.16) on montre directement que
2
T
Y
L
PO
N
H
EC
E
U
IQ
∂2φ
∂ φ
∂ φ
1 ∂ 2 ∂φ
ȧ ∂φ
R
=
.
=
−
+3
µ
ν
2
2
2
∂ x̃ ∂ x̃
∂T
R ∂R ∂R
∂t
a ∂t
L’équation pour un champ scalaire spatialement homogène est donc
E
L
O
η µν
ÉC
2
(4.76)
∂2φ
ȧ ∂φ
+ V (φ) = 0 .
+3
(4.77)
∂t2
a ∂t
Nous aurons besoin de cette équation car un champ scalaire n’a pas en général une
dépendance simple dans le temps pour la densité d’énergie et il n’y a pas une forme de
l’équation de Friedmann analogue à (4.64). Dans les situations où l’univers est dominé
par un champ scalaire spatialement homogène, on utilise en général (4.77) couplé à
l’équation de Friedmann :
Å ã2
k
8πGV (φ)
ȧ
+ 2 .
=
(4.78)
a
3
a
U
Q
I
N
Incidemment, (4.76) nous dit qu’un champ qui dépend du temps mais est spatialement homogène dans des coordonnées comobiles doit être spatialement inhomogène
dans des coordonnées en chute libre. Cela provient de ce que la synchronisation des
horloges est diﬀérente dans les deux systèmes. En conséquence, une dépendance temporelle dans l’un induit une dépendance spatiale dans l’autre.
Un dernier mot sur la « réalité » des champs scalaires. Comme c’est le cas pour les
champs électrique et magnétique, l’existence d’un champ scalaire cosmologique peut
être déduit de l’observation du mouvement de particules test. En particulier, nous
verrons (4.94) qu’un champ scalaire homogène avec V > 0 fait accélérer les particules
en les éloignant les unes des autres.
ÉC
E
L
O
Y
L
PO
H
C
TE
E
Le tenseur de Riemann
6
N
H
EC
E
U
IQ
175
Le tenseur de Riemann
T
Y
L
PO
Nous avons maintenant tous les résultats nécessaires pour faire de la cosmologie
homogène. Le lecteur impatient a donc notre permission pour sauter directement au
chapitre 5. Cependant, pour déduire les équations générales des champs et mieux
comprendre la physique de la gravitation, il faut faire un petit eﬀort supplémentaire.
Jusqu’à présent, il apparaît que le champ gravitationnel est caractérisé par les 256
composantes du tenseur gµν,αβ qui apparaît dans la métrique (4.4) d’un système en
chute libre. Les composantes ne sont pas toutes indépendantes et nous avons manifestement une liberté énorme pour les changer en faisant des changement de coordonnées
arbitraires. Pour notre métrique locale dans un univers homogèène, nous avons deux
quantités, les coeﬃcients α et β de (4.23).
Pour mieux comprendre la signiﬁcation physique des gµν,αβ , il faut voir leur eﬀet
sur le mouvement des particules. Au chapitre 3 nous avons vu que des particules libres
suivent des trajectoires qui maximisent leur temps propre, c’est-à-dire des géodésiques
de l’espace-temps. L’équations des géodésiques est
Å
ã
d
dxν
1 ∂gλν dxλ dxν
= 0
µ = 0, 1, 2, 3 .
(4.79)
gµν (x)
−
dτ
dτ
2 ∂xµ dτ dτ
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
Si on l’applique à la métrique (4.4), l’équation de la géodésique est, au premier ordre
en x̃,
ÉC
E
L
O
d2 x̃α
dx̃µ dx̃ν
.
= −η αγ [gµγ,νβ − (1/2)gµν,γβ ] x̃β
2
dτ
dτ dτ
(4.80)
Il est intéressant de considérer le mouvement d’une particule lente, c’est-à-dire une
trajectoire avec dx̃0 /dτ ∼ 1, dx̃i /dτ ∼ 0, i = 1, 3. Dans ce cas, (4.80) devient
d2 x̃i
= −(1/2) g00,iµ x̃µ
dτ 2
i = 1, 2, 3 ,
(4.81)
où nous avons supposé que la métrique est orthogonale gµ=ν = 0. Pour la métrique
(4.23) ceci devient
ï ò
ä
d2 x̃i
i
= α x̃ =
x̃i
i = 1, 2, 3 .
(4.82)
2
dτ
a t0
H
C
TE
U
Q
I
N
Alors que l’interprétation de (4.82) est relativement simple, il faut prendre des
précautions pour interpréter l’accélération d’une particule par rapport à un réseau
de coordonnées en principe arbitraire. La seule accélération qui ait une signiﬁcation
physique est l’accélération par rapport à d’autres particules. Par exemple, en électrodynamique, l’accélération de particules chargées par rapport aux particules neutres
signale la présence d’un champ électromagnétique. En gravitation, toutes les particules
qui sont au même point ont la même accélération à cause du principe d’équivalence.
La présence d’eﬀets gravitationnels ne peut être signalée que par l’accélération relative
ÉC
E
L
O
Y
L
PO
E
176
ÉC
E
U
IQ
Chapitre 4. Les équations du champ gravitationnel
E
L
O
T
Y
L
PO
N
H
EC
t
t2
(t,x b )
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
(t,x a)
t1
x
Fig. 4.2: Trajectoires de deux particules test xa (t) et xb (t). Les particules démarrent à t = 0
avec la même vitesse, dans ce cas dx/dt = 0. La séparation des deux particules est mesurée
par un observateur à l’origine équipé d’une horloge et d’un radar. Le carré de la séparation
µ
ν
ν
spatiale δ 2 (t) = −ηµν (xµ
a − xb )(xa − xb ) est égal au carré du temps de vol aller et retour des
2
photons, (t2 − t1 ) . S’il y a un champ gravitationnel, les particules test ont une accélération
relative et δ 2 change avec le temps.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Le tenseur de Riemann
T
Y
L
PO
N
H
EC
E
U
IQ
177
de particules tests séparées par des distances petites mais non-nulles. De tels eﬀets
existent à cause des eﬀets de marée dans les champs gravitationnels inhomogènes.
Par conséquent, nous comparons le mouvement de deux particules test (m → 0)
au voisinage de x̃ = 0 avec des coordonnées spatiales initiales (ﬁgure 4.2) (x̃0 = 0)
ÉC
E
L
O
x̃ia (t = τa = 0) = −i /2
(particule a)
(4.83)
x̃ib (t = τb = 0) = +i /2
(particule b)
(4.84)
pour i = 1, 2, 3. Comme indiqué sur la ﬁgure, nous faisons démarrer leurs horloges
propres respectives qui mesurent leur temps propre à l’instant t = 0. Nous supposons
que les deux particules démarrent avec la même vitesse :
dx̃µb
dx̃µa
(t = 0) =
(t = 0) ≡ v µ .
dτa
dτb
N
H
EC
E
U
IQ
(4.85)
Une mesure appropriée de la séparation des deux particules est l’analogue spatial du
temps propre, la distance propre :
LY T
δ 2 (t) = − [ηµν (x̃µa − x̃µb )(x̃νa − x̃νb )]x̃0 =x̃0 =t .
O
P
E
L
ÉCO
a
(4.86)
b
Comme on l’illustre dans la ﬁgure 4.2, cette quantité peut être mesurée par l’observateur à l’origine avec un radar et une horloge.
A cause de la symétrie de la situation, nous pouvons utiliser soit le temps-coordonnée
t ou le temps propre commun τ des deux particules pour paramétrer les trajectoires.
A τ = 0 on a
δ 2 (τ = 0) = − [ηµν (x̃µa − x̃µb )(x̃νa − x̃νb )]τ =0 = −ηµν µ ν .
(4.87)
Après un petit temps propre τ les coordonnées sont
x̃µ (τ ) = x̃µ (τ = 0) + τ
1 d2 x̃µ
dx̃µ
(0) + τ 2
(0) ,
dτ
2
dτ 2
(4.88)
où d2 x̃µ /dτ 2 est donné par (4.80). En utilisant les positions et vitesses initiales des
particules a et b, on trouve qu’après un temps propre τ , la séparation invariante est
δ 2 (τ ) = δ 2 (0) − τ 2 Rαµβν (x̃ = 0) α v µ β v ν ,
où Rκλµν est le tenseur de courbure de Riemann :
Y
L
PO
H
C
TE
1
Rκλµν (x̃ = 0) = [gκµ,λν − gλµ,κν − gκν,λµ + gλν,κµ ]x̃=0 .
2
E
L
O
U
Q
I
N
(4.89)
(4.90)
En l’absence de gravitation (espace-temps plat), gµν = ηµν ⇒ gµν,αβ = 0, et le
tenseur de Riemann s’annule. Par conséquent, dans ce cas la séparation des deux
particules est indépendante du temps.
ÉC
E
178
E
U
IQ
Chapitre 4. Les équations du champ gravitationnel
T
Y
L
PO
N
H
EC
L’accélération relative non-nulle des deux particules test voisines est appelée la
« déviation géodésique ». Comme nous l’avons déjà fait remarquer, c’est la véritable
manifestation de la présence d’un champ gravitationnel. Par exemple, deux particules
test lâchées dans le champ gravitationnel de la Terre (ﬁgure 3.4) vont tomber vers
le centre de la Terre. Un observateur en chute libre verra les deux particules accélérer l’une vers l’autre. Cette convergence est régie par le tenseur de Riemann de la
Terre. Dans l’exercice 4.6, nous utiliserons la dynamique newtonienne pour calculer
les composantes Rµ0ν0 .
Nous allons maintenant appliquer ces résultats au cas de notre système cosmologique en chute libre avec la métrique (4.23). Nous considérons deux particules qui
sont initialement au repos (v 0 = 1, v i = 0) comme sur la ﬁgure 4.2. La particule
a est initialement en (x̃1 = δ/2, x̃2 = x̃3 = 0) et la particule b est initialement en
(x̃1 = −δ/2, x̃2 = x̃3 = 0). Leur séparation initiale est ηµν µ ν = δ 2 . L’équation
(4.89) devient
ÉC
E
L
O
d2 δ
d2 δ 2
∼ 2δ 2 = −2R1010 δ 2 ,
2
dτ
dτ
T
Y
L
PO
N
H
EC
E
U
IQ
(4.91)
où nous avons utilisé dδ/dτ = 0 à τ = 0.
Le tenseur de Riemann se calcule aisément pour la métrique (4.23) :
ÉC
E
L
O
R1010 = −α = −
ä
.
a
(4.92)
Nous verrons bientôt que le tenseur de Riemann est déterminé par le tenseur énergieimpulsion au travers de l’équation d’Einstein. Dans le cas d’un univers homogène,
nous avons déjà trouvé (4.59) :
ä
4πG(ρ + 3p)
= −
,
a
3
(4.93)
d2 δ
4πG
(ρ + 3p) δ .
= −
dτ 2
3
(4.94)
ce qui implique
U
Q
I
N
En supposant que la pression est négligeable en comparaison de la densité d’énergie,
c’est-à-dire un univers dominé par de la matière non-relativiste, et en choisissant
comme coordonnée radiale d’une particule R = δ/2 on trouve
d2 R
GM (R)
= −
,
dτ 2
R2
Y
L
PO
H
C
TE
(4.95)
où M (R = δ/2) est la masse à l’intérieur d’une sphère imaginaire de rayon R centrée à
l’origine. Cette accélération est la même que celle calculée au chapitre 1 en utilisant un
argument newtonien. Cela explique pourquoi l’argument newtonien donne la bonne
équation de Friedmann.
ÉC
E
L
O
E
Un univers avec ρ = 0
7
Un univers avec ρ = 0
T
Y
L
PO
N
H
EC
E
U
IQ
179
Sans connaître l’équation d’Einstein, on peut deviner l’équation de Friedmann
pour un univers avec ρ = 0. Dans ce cas, il n’y a pas de gravitation et le tenseur de
Riemann (4.90) s’annule. Pour la métrique (4.23) cela implique
Å ã2
ȧ
ä
k
= 0
β=
α=
+ 2 = 0.
(4.96)
a
a
a
ÉC
E
L
O
Puisque α = β = 0, la métrique (4.23) est globalement lorentzienne.
Il y a deux solutions à (4.96). La première est a(t) = a = constante avec k = 0 :
dτ 2 = dt2 − a2 [dr2 + r2 (dθ2 + sin2 θdφ2 )] .
(4.97)
Cette solution donne directement la métrique localement lorentzienne (4.23) avec
R = ar et T = t.
La deuxième solution est a = t avec k = −1, c’est-à-dire
ï
ò
dr2
2
2
2
2
2
2
2
+ r (dθ + sin θ dφ ) .
(4.98)
dτ = dt − t
1 + r2
T
Y
L
PO
N
H
EC
E
U
IQ
Dans ce cas, les transformations (4.12) et (4.11) sont équivalentes à
R = rt ,
T = t 1 + r 2 − t0 .
E
L
O
(4.99)
Ces transformations donnent exactement une métrique lorentzienne :
ÉC
dτ 2 = dT 2 − dR2 − R2 (dθ2 + sin2 θdφ2 )
= dT 2 − dX 2 − dY 2 − dZ 2 .
(4.100)
Il est peut-être surprenant qu’un univers avec un espace-temps plat puisse être
décrit par la métrique de Robertson–Walker avec k = −1 et a(t) = t. Pour lever ce
paradoxe, il faut se rappeler la diﬀérence entre des espaces courbes et des espacetemps courbes. La courbure de l’espace se voit en faisant instantanément des mesures
géométriques, par exemple en vériﬁant la relation euclidienne Rdθ = dS comme sur
la ﬁgure 3.6. Puisque la mesure a lieu sur de grandes distances, il faut un réseau
d’horloges et il faut décider comment les synchroniser. Toute conclusion sur le fait
que l’espace soit plat ou non dépend nécessairement de ces conventions. Comme nous
l’avons vu sur l’exemple d’un univers avec ρ = 0, le choix d’horloges comobiles donne
un espace courbe alors que le choix d’horloges du laboratoire donne une espace plat.
La courbure de l’espace-temps se voit en suivant les trajectoires de particules
test proches comme l’illustre la ﬁgure 4.2. La mesure est faite dans un système de
coordonnées en chute libre dans lequel les particules ont la même vitesse initiale. Si
la séparation entre les particules est indépendante du temps, l’espace-temps est plat.
Contrairement aux mesures de courbure spatiale qui sont faites instantanément sur
de grandes distances, les mesures de courbure d’espace-temps sont faites localement
mais demandent une durée non-nulle. Elles ne requièrent qu’un seul observateur avec
une horloge.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
180
E
U
IQ
Chapitre 4. Les équations du champ gravitationnel
8
N
H
EC
Le tenseur d’Einstein
T
Y
L
PO
Les coeﬃcients des termes quadratiques dans la métrique localement lorentzienne
(4.4) ou (4.23) sont déterminés par la densité d’énergie et la pression au travers de
l’équation d’Einstein :
ÉC
E
L
O
Gµν (x̃ = 0) = −8πG T µν (x̃ = 0) ,
µν
(4.101)
µν
où T est le tenseur énergie-impulsion (section 2) et où G est le tenseur d’Einstein.
Puisque les eﬀets physiques de la gravitation sont déterminés par le tenseur de Riemann, on peut s’attendre à ce que les composantes de Gµν soient des combinaisons linéaires des Rαβγδ . La conservation locale de l’énergie impose que la quadri-divergence
de Gµν s’annule :
ò
ï
∂Gµν
= 0.
(4.102)
∂ x̃µ x̃=0
E
U
IQ
Il se trouve (exercice 4.4) qu’il n’y a qu’une seule combinaison des Rµναβ qui ait cette
propriété :
N
H
EC
Gµν (x̃ = 0) = η µα η νβ Gαβ (x̃ = 0) ,
avec
T
Y
L
PO
Gµν (x̃ = 0) = η
E
L
O
λκ
ã
Å
1
αβ
Rλµκν (0) − ηµν η Rλακβ (0) .
2
(4.103)
Mis à part un facteur numérique, on voit que la conservation de l’énergie détermine la
forme de l’équation d’Einstein (4.101). On trouve le facteur de proportionnalité 8πG
en prenant la limite newtonienne (exercice 4.6).
La forme du tenseur d’Einstein est relativement simple pour un système de coordonnées orthogonal (gκ=λ = 0) :
Å 2
ã
∂ gλλ
∂ 2 gµµ
η λλ
+
Gµµ (x̃ = 0) = (1/2)
∂xµ ∂xµ
∂xλ ∂xλ
ÉC
λ=µ
− (1/2)ηµµ
η λλ η αα
λ α=λ
∂ 2 gλλ
.
∂xα ∂xα
(4.104)
Il est donc simple de calculer le tenseur d’Einstein pour la métrique (4.23) de notre
système en chute libre Gµ=ν (0) = 0 et
ñ Å ã2
ô
ȧ
k
G00 (0) = −3β = −3
+ 2
(4.105)
a
a t
Y
L
PO
ñ
G11 (0) = G22 (0) = G33 (0) = 2α + β =
E
L
O
H
C
TE
ä
2 +
a
0
ô
Å ã2
ȧ
k
+ 2
.
a
a t
U
Q
I
N
(4.106)
0
En substituant ces fonctions dans (4.101), on trouve l’équation de Friedmann (4.57)
et sa partenaire (4.58).
ÉC
E
L’équation d’Einstein générale
9
N
H
EC
E
U
IQ
181
L’équation d’Einstein générale
T
Y
L
PO
Dans la section 8, nous avons trouvé le tenseur d’Einstein (4.103) à l’origine d’un
système de coordonnées en chute libre, qui peut être utilisé dans l’équation des champs
d’Einstein (4.101). Puisque le principe d’équivalence nous assure qu’il est toujours possible de trouver un système de coordonnées en chute libre, (4.101) contient toute la
physique de la gravitation. Cela est illustré par le fait que nous avons utilisé ces équations pour trouver l’équation de Friedmann qui s’applique partout dans un univers
homogène, pas seulement à l’origine.
Cependant, pour appliquer (4.101), nous avons d’abord eu besoin de transformer
les coordonnées comobiles en coordonnées en chute libre. Même si c’est une procédure
relativement simple, il est utile d’avoir la généralisation de (4.101) qui s’applique à
un système de coordonnées général.
Pour le faire, nous considérons des coordonnées (xµ , µ = 0, 1, 2, 3) qui sont des
fonctions xµ (x̃ν ) des coordonnées en chute libre x̃ν . La métrique gαβ pour les coordonnées xµ est facile à calculer :
ÉC
E
L
O
N
H
EC
dτ 2 = gµν (x) dxµ dxν = gαβ (x̃)dx̃α dx̃β
c’est-à-dire
ÉC
E
L
O
T
Y
L
PO
= gαβ (x̃)
E
U
IQ
∂ x̃α ∂ x̃β µ ν
dx dx ,
∂xµ ∂xν
(4.107)
gµν (x) =
∂ x̃α ∂ x̃β
gαβ (x̃) ,
∂xµ ∂xν
(4.108)
gαβ (x̃) =
∂xµ ∂xν
gµν (x) .
∂ x̃α ∂ x̃β
(4.109)
ou
Il sera utile de déﬁnir la métrique inverse g αµ :
g αµ gµβ = δ α β ,
(4.110)
où δ α β = 1 si α = β et δβα = 0 si α = β. Les métriques inverses de deux systèmes
sont reliées par
g µν (x) =
ou
ÉC
Y
L
PO
∂ x̃α ∂ x̃β µν
(x̃) =
g (x) .
∂xµ ∂xν
E
L
O
g
αβ
H
C
TE
∂xµ ∂xν αβ
g (x̃) ,
∂ x̃α ∂ x̃β
On peut vériﬁer cette équation en la multipliant par (4.109).
U
Q
I
N
(4.111)
(4.112)
E
182
E
U
IQ
Chapitre 4. Les équations du champ gravitationnel
T
Y
L
PO
N
H
EC
L’équation (4.101) contient des dérivées de la métrique gµν (x̃) du système x̃. Nous
voudrions transformer (4.101) de façon qu’elle contienne les dérivées de la métrique
gµν (x) du système x. En nous inspirant d’une transformation de Lorentz, nous déﬁnissons les tenseurs Gµν et Tµν dans le système x par
ÉC
E
L
O
Gµν (x) ≡
∂ x̃α ∂ x̃β
Gαβ (x̃ = 0)
∂xµ ∂xν
Tµν (x) ≡
∂ x̃α ∂ x̃β
Tαβ (x̃ = 0)
∂xν ∂xµ
x = x(x̃ = 0)
(4.113)
x = x(x̃ = 0) .
(4.114)
En appliquant cette transformation aux deux membres de (4.101) on trouve trivialement que
Gµν (x) = 8πG Tµν (x)
x = x(x̃ = 0) .
N
H
EC
E
U
IQ
(4.115)
Une forme explicite pour Gµν (x) peut être obtenue en substituant (4.103) dans
(4.113) et en utilisant (4.112) :
ã
Å
1
λκ
αβ
Gµν (x) = g
(4.116)
Rλµκν (x) − gµν g Rλακβ (x) ,
2
où
ÉC
E
L
O
Rκλµν (x) ≡
T
Y
L
PO
∂ x̃α ∂ x̃β ∂ x̃γ ∂ x̃δ
Rαβγδ (x̃ = 0)
∂xκ ∂xλ ∂xµ ∂xν
x = x(x̃ = 0) .
(4.117)
En reportant (4.90) dans (4.117) et en utilisant (4.109), on trouve (après un calcul
assez long)
Rκλµν (x) =
1
(gκµ,λν − gλµ,κν − gκν,λµ + gλν,κµ )
2
+ gησ ( Γηκµ Γσλν − Γηκν Γσλµ ) ,
où la « connexion aﬃne » Γ est déﬁnie par
Å
ã
∂gκν
∂gκµ
∂gµν
+
−
.
Γηκµ ≡ (1/2)g ην
∂xκ
∂xµ
∂xν
H
C
TE
(4.118)
U
Q
I
N
(4.119)
Notons que pour trouver (4.118), il est peut-être plus simple de procéder à l’envers
en montrant que
Y
L
PO
∂xκ ∂xλ ∂xµ ∂xν
Rαβγδ (x̃ = 0) =
Rαβγδ (x)
∂ x̃α ∂ x̃β ∂ x̃γ ∂ x̃δ
ÉC
E
L
O
x = x(x̃ = 0) ,
où Rαβγδ (x̃ = 0) est donné par (4.90) et où Rαβγδ (x) est donné par (4.118).
(4.120)
E
L’équation d’Einstein générale
T
Y
L
PO
N
H
EC
E
U
IQ
183
L’équation (4.118) est la forme générale du tenseur de Riemann. Les termes contenant la connexion aﬃne n’étaient pas présents dans la forme (4.90) parce que les dérivées premières de la métrique s’annulent à l’origine d’un système de coordonnées en
chute libre.
Les équations (4.116), (4.118) et (4.119) déterminent le membre de gauche de
l’équation d’Einstein (4.115) sans faire référence explicite au système en chute libre.
Aﬁn de trouver le membre de droite (4.114) de (4.115), le plus simple est de déﬁnir
T µν par
ÉC
E
L
O
∂xµ ∂xν αβ
T (x̃ = 0)
∂ x̃α ∂ x̃β
T µν (x) ≡
x = x(x̃ = 0) .
(4.121)
Il est facile de montrer que
Tµν (x) = gµα (x) gνβ (x) T αβ (x) .
En utilisant T00 = ρ et Tii = p, on trouve
T µν (x) =
où
ÉC
E
L
O
N
H
EC
∂xµ ∂xν
∂xµ ∂xν
ρ +
p
0
0
∂ x̃ ∂ x̃
∂ x̃i ∂ x̃i
T
Y
L
PO
E
U
IQ
= U µ U ν ρ + ( U µ U ν − g µν )p ,
Uµ =
∂xµ
∂ x̃0
(4.122)
(4.123)
(4.124)
est la quadri-vitesse de x par rapport à x̃. Puisque l’impulsion moyenne des particules
s’annule dans le système x̃, U µ est aussi la quadri-vitesse des particules dans le système
x.
L’équation d’Einstein (4.115) avec (4.116), (4.118) et (4.119) dans le membre de
gauche et (4.123), (4.124) et (4.122) dans celui de droite est la généralisation tant
attendue de (4.101).
Pour vériﬁer ce résultat, nous allons appliquer (4.115) à la métrique de Robertson–
Walker :
gtt =
grr
ÉC
1
= 1
g tt
1
−a2
= rr =
g
1 − kr2
E
L
O
gθθ =
Y
L
PO
1
= −a2 r2
g θθ
U
Q
I
N
(4.125)
H
C
TE
(4.126)
(4.127)
E
184
E
U
IQ
Chapitre 4. Les équations du champ gravitationnel
1
T
Y
L
PO
gφφ =
g φφ
N
H
EC
= −a2 r2 sin2 θ .
(4.128)
si µ = ν
(4.129)
Le tenseur d’Einstein est
ÉC
E
L
O
Gµν = 0
G00
ñ
Gii =
ô
ñÅ ã2
k
ȧ
= −3
+ 2
a
a
ä
2 +
a
(4.130)
ô
Å ã2
ȧ
k
+ 2 gii
a
a
i = r, θ, φ .
(4.131)
E
U
IQ
En coordonnées comobiles, la vitesse moyenne des particules s’annule (U 0 =
1, U i = 0). L’équation (4.123) pour le tenseur énergie-impulsion avec (4.122) donne
Tµ=ν = 0 et
T00 = ρ
T
Y
L
PO
Tii = −p gii
E
L
O
N
H
EC
i = r, θ, φ .
(4.132)
(4.133)
En combinant ces expressions du tenseur d’Einstein avec les expressions du tenseur
énergie-impulsion, on obtient à nouveau (4.57) et (4.58).
Remarquons avec une satisfaction non dissimulée qu’en raison du grand nombre
de termes qui s’annulent l’un l’autre, les équations ﬁnales ne dépendent pas des coordonnées spatiales (r, θ, φ). Cela conﬁrme le fait que la métrique de Robertson–Walker
s’applique à un univers homogène. Si nous avions renplacé le facteur 1/(1 − kr2 )
dans la métrique par un facteur général f (r), la forme de l’équation d’Einstein aurait
été plus compliquée mais nous aurions obtenu f (r) = 1/(1 − kr2 ) comme solution.
Les arguments du chapitre 3 que nous avons utilisés pour trouver la métrique de
Robertson–Walker n’étaient donc pas nécessaires car la forme de la métrique nous
aurait été de toute façon imposée par l’équation d’Einstein .
Terminons ce chapitre avec quelques commentaires sur la « généralité » de la
relativité générale. On tire beaucoup du fait que cette théorie traite les systèmes
de coordonnées arbitraires. Les manipulations que nous venons d’eﬀectuer montrent
qu’il n’y a rien de très profond là-dedans. On aurait pu commencer avec la métrique
de la relativité restreinte ηµν , en faisant ensuite des changements de coordonnées
arbitraires pour mettre la métrique sous une forme aussi étrange que l’on veut. Ce
qui est important, dans ce chapitre, est que nous ne sommes pas partis de ηµν mais
plutôt d’une métrique localement lorentzienne contrainte par l’équation d’Einstein
pour un système en chute libre. La partie essentielle de la physique est contenue dans
le principe d’équivalence qui assure que nous pouvons trouver de telles coordonnées
en chute libre, et dans la conservation de l’énergie locale qui contraint la métrique de
telles coordonnées.
ÉC
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Exercices sur le chapitre 4
Exercices
T
Y
L
PO
N
H
EC
E
U
IQ
185
4.1 Un intervalle de temps dt dans notre système en chute libre est, d’après (4.11),
donné par
ÉC
E
L
O
dT = dt + aȧrdr + (1/2)ȧ2 r2 dt + (1/2)aär2 dt .
(4.134)
(a) Montrer que si ä = 0 (c’est-à-dire en l’absence de gravitation) la relation entre dT
et dt provient simplement de la dilatation des temps de la relativité restreinte entre
des horloges ﬁxes et (co)mobiles.
(b) Vériﬁer (4.12) et (4.11).
4.2 Vériﬁer que Gµν donné par (4.103) et (4.90) satisfait
∂Gµν
= 0.
∂xµ
T
Y
L
PO
N
H
EC
E
U
IQ
(4.135)
4.3 Considérons le tenseur énergie-impulsion (4.30) de particules libres.
(a) Montrer que la pression p déﬁnie par (4.35) est en accord avec les relations
habituelles satisfaites par un gaz parfait de température T : p = nT pour un gaz
non-relativiste et p = ρ/3 pour un gaz relativiste.
(b) Utiliser l’équation de Liouville pour montrer que T µν donné par (4.30) satisfait
ÉC
E
L
O
∂T µν
= 0.
∂xµ
(4.136)
4.4 Montrer que le tenseur de Riemann (4.90) et le tenseur d’Einstein (4.103) sont
des tenseurs de Lorentz. Cela montre que l’équation d’Einstein (4.101) est invariante
de Lorentz.
4.5 Montrer que l’équation d’Einstein est équivalente à
Rµν = −8πG (Tµν − (1/2)gµν g αβ Tαβ ) ,
où Rµν est le tenseur de Ricci
Y
L
PO
Rµν = g αβ Rαµβν .
E
L
O
H
C
TE
U
Q
I
N
(4.137)
(4.138)
4.6 Nous voulons prendre la limite newtonienne de l’équation d’Einstein pour justiﬁer
le facteur 8π.
ÉC
E
186
E
U
IQ
Chapitre 4. Les équations du champ gravitationnel
T
Y
L
PO
N
H
EC
(a) Considérons deux particules test n’ayant que des interaction gravitationnelles placées dans une sphère de densité uniforme ρ et de pression p ρ. Utiliser la gravitation
newtonienne pour calculer l’accélération relative des deux particules initialement au
repos et séparées par δ. En utilisant (4.91), montrer que dans un système de coordonnées en chute libre tombant avec les deux particules, les composantes Ri0i0 du tenseur
de Riemann sont
ÉC
E
L
O
Ri0i0 =
4πGρ
3
i = 1, 2, 3 .
(4.139)
Il s’ensuit que
R00 = −4πGρ .
(4.140)
E
U
IQ
Cela est cohérent avec (4.137), ce qui justiﬁe donc le facteur 8π dans l’équation d’Einstein .
(b) Utiliser la gravitation newtonienne pour calculer l’accélération relative des quatre
particules de la ﬁgure 3.4. Trouver les composantes R0i0i du tenseur de Riemann dans
le système en chute libre et montrer que
T
Y
L
PO
R00 = 0 .
N
H
EC
(4.141)
Ce résultat est cohérent avec (4.137) dans le vide.
ÉC
E
L
O
4.7 La « vitesse instantanée » d’une galaxie à (t, χ) est
d(aχ)
ȧ
aχ
= (aχ)
=
.
dt
a
dH
(4.142)
Cette vitesse est plus grande que c = 1 pour aχ plus grand que la distance de Hubble.
Cela n’est pas en contradiction avec la relativité restreinte qui ne s’applique qu’aux
systèmes de coordonnées lorentziens. Dans notre système en chute libre x̃, les vitesses
galactiques sont toujours inférieures à c mais, en tout état de cause, le système ne
s’applique qu’à R ∼ aχ dH .
Considérons un univers avec ρ = 0. Cet univers peut avoir un système de coordonnées globalement lorentziennes déﬁnies par (4.99)
(4.143)
R = rt ,
T = t 1 + r 2 − t0 .
H
C
TE
U
Q
I
N
Considérons une particule test à une valeur ﬁxée de r. Montrer que dans le système
(T, R) les vitesses sont toujours inférieures à c = 1, dR/dT < 1.
Montrer que l’équation du mouvement pour un photon se dirigeant vers l’origine
est
ÉC
E
L
O
Y
L
PO
aχ
d(aχ)
=
−1.
dt
dH (t)
(4.144)
E
Exercices sur le chapitre 4
T
Y
L
PO
N
H
EC
E
U
IQ
187
La distance ne décroît que si la particule est à une distance plus proche que le rayon de
Hubble. Au rayon de Hubble, la vitesse instantanée s’annule. Bien entendu, l’équation
dχ/dt = −1/a garantit que tous les observateurs locaux voient le photon se propager
à la vitesse de la lumière.
ÉC
E
L
O
4.8 Les équations des champs d’Einstein pour la métrique (3.17) se trouvent aisément
si |Φ| 1 car dans ce cas on peut ignorer les termes proportionnels à la connexion
aﬃne dans (4.118) qui sont du second ordre en Φ. Montrer que dans la limite d’une
pression nulle, les équations des champs donnent l’équation de Poisson pour le potentiel gravitationnel Φ.
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
E
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
ÉC
N
H
EC
T
Y
L
PO
E
L
O
E
U
IQ
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
E
T
Y
L
PO
N
H
EC
E
U
IQ
E
L
5
CO
ÉChapitre
Applications de l’équation de
Friedmann
T
Y
L
PO
N
H
EC
E
U
IQ
L’évolution dans le temps du paramètre d’échelle a(t) est déterminée par deux
équations couplées. La première est l’équation de Friedmann :
Å ã2
8πGρ
ȧ
+ H02 (1 − ΩT ) â−2 ,
=
(5.1)
a
3
ÉC
E
L
O
où ΩT est la densité totale actuelle divisée par la densité critique
ΩT =
ρ(a0 )
,
3H02 /8πG
(5.2)
et où
H −1
a0 = 0
|1 − ΩT |
â(t) =
a(t)
.
a0
(5.3)
La seconde équation est « l’équation d’état » dont le rôle est de donner la pression en
fonction de la densité d’énergie ρ. Cela détermine, au travers de la loi locale de conservation de l’énergie (4.45), la dépendance de ρ dans le paramètre d’échelle qui peut
alors être imposée dans l’équation de Friedmann. Pour un mélange de matière nonrelativiste, de matière relativiste, et d’énergie du vide, on obtient la densité d’énergie
en combinant (4.46), (4.47) et (4.48), et l’équation de Friedmann prend la forme :
H
C
TE
1/2
ȧ
= H0 ΩR â−4 + ΩM â−3 + ΩΛ + (1 − ΩT )â−2
,
a
Y
L
PO
U
Q
I
N
(5.4)
où ΩR , ΩM , et ΩΛ sont les contributions actuelles de matière relativiste, de matière
relativiste, et d’énergie du vide :
ÉC
E
L
O
ΩT = ΩR + ΩM + ΩΛ .
189
(5.5)
E
190
E
U
IQ
Chapitre 5. Applications de l’équation de Friedmann
T
Y
L
PO
N
H
EC
Insistons sur le fait que le terme ΩR dans (5.4) est « fragile » car les particules qui
ne sont pas relativistes aujourd’hui le furent dans le passé. Il est donc nécessaire de
prendre un certain soin dans les calculs où ce terme est important, (voir par exemple
l’exercice 5.2).
L’équation de Friedmann (5.4) permet de calculer la plupart des grandeurs intéressantes dans un univers homogène. Par exemple, le temps en fonction du paramètre
d’échelle est :
a(t)
da
t − t1 =
a (ȧ/a)
a1
ÉC
E
L
O
= H0−1
a(t)
a1
da
a (ΩR
â−4
+ ΩM
â−3
N
H
EC
La coordonnée radiale χ d’un objet de redshift z est
a0
da
χ(z) =
2 (ȧ/a)
a
a0 /(1+z)
E
L
O
H −1
= 0
a0
ÉC
1
(1+z)−1
T
Y
L
PO
â2
(ΩR
â−4
+ ΩM
â−3
E
U
IQ
1/2
.
(5.6)
1/2
.
(5.7)
+ ΩΛ + (1 − ΩT )â−2 )
dâ
+ ΩΛ + (1 − ΩT )â−2 )
Connaissant χ(z), on peut calculer la distance de luminosité et la distance angulaire :
dL (z) = a0 r(z)(1 + z)
(5.8)
dA (z) = a0 r(z)/(1 + z) ,
(5.9)
où la coordonnée radiale r est
r =
sin χ = χ − χ3 /6 + .....
χ
sinh χ = χ + χ3 /6 + .....
ΩT > 1
ΩT = 1 .
ΩT < 1
H
C
TE
U
Q
I
N
(5.10)
Les intégrales (5.6) et (5.7) sont fonction des paramètres cosmologiques (H0 , ΩR ,
ΩM , ΩΛ ) et, dans ce chapitre, nous montrerons comment cela peut être utilisé pour
contraindre leur valeur.
Dans la section 1, nous calculerons ce que l’on appelle communément « l’âge de
l’univers » en fonction de (ΩM , ΩΛ ). Nous obtiendrons une contrainte sur ces deux
paramètres en imposant que l’âge calculé soit supérieur à l’âge des objets les plus
anciens connus dans l’univers.
ÉC
E
L
O
Y
L
PO
E
L’âge de l’univers
T
Y
L
PO
N
H
EC
E
U
IQ
191
Dans la section 2, nous calculerons l’intégrale (5.7) et nous montrerons comment les
distances de luminosité et les distances angulaires peuvent être utilisées pour mesurer
(ΩM , ΩΛ ).
Dans les sections suivantes, nous examinerons deux problèmes de la cosmologie
classique, le problème de « l’horizon » et le problème des « Ω ». Nous montrerons
alors que ces deux problèmes peuvent, en un certain sens, être résolus par les modèles
inﬂationnaires de l’univers primordial.
Nous terminerons le chapitre avec une discussion de l’absorption et de la diﬀusion
des photons dans l’espace intergalactique. L’absence d’absorption observée pour les
photons ultraviolets de quasars à grand redshift démontrera que la plupart des baryons
intergalactiques ont été réionisés à un moment plus précoce qu’un redshift de ∼ 5.
ÉC
1
E
L
O
L’âge de l’univers
E
U
IQ
Le temps qui s’est écoulé depuis la singularité initiale (a = 0) peut être calculé
avec (5.6). La durée de l’époque de rayonnement est négligeable (exercice 5.2), nous
pouvons donc ignorer le terme relativiste dans l’intégrand de (5.6). Dans cette approximation, l’âge calculé est H0−1 multiplié par une fonction de (ΩM , ΩΛ ) :
a0
da
t0 =
ȧ
0
ÉC
E
L
O
∼ H0−1
T
Y
L
PO
1
0
N
H
EC
dâ
â (ΩM
â−3
1/2
+ ΩΛ + (1 − ΩM − ΩΛ )â−2 )
.
(5.11)
Sauf si l’intégrand a un comportement irrégulier, l’ordre de grandeur de l’âge est
le temps de Hubble tH = H0−1 . L’âge peut se calculer très simplement dans deux cas :
10
t0 = tH = 1.4 h−1
70 × 10 an
10
t0 = (2/3)tH = 0.9 h−1
70 × 10 an
(ΩM = ΩΛ = 0) ,
(5.12)
(ΩM = 1, ΩΛ = 0) .
(5.13)
Avec les valeurs des paramètres cosmologiques préférées actuellement, on trouve numériquement
t0 ∼ tH = 1.4
h−1
70
× 10
10
an
H
C
TE
(ΩM = 0.3, ΩΛ = 0.7) .
U
Q
I
N
(5.14)
Les contours d’âge calculé en unités de H0−1 sont montrés sur la ﬁgure 5.1 en
fonction de (ΩM , ΩΛ ). On voit que l’âge est une fonction décroissante de ΩM . C’est
simplement dû à ce que la gravitation « normale » freine l’expansion, ä < 0. Puisque
la valeur actuelle de ȧ/a0 est ﬁxée (= H0 ), toute décélération impliquerait une valeur
supérieure de ȧ/a0 dans le passé et, par conséquent, un temps plus court pour aller
de a = 0 à a = a0 .
ÉC
E
L
O
Y
L
PO
E
192
ÉC
E
U
IQ
Chapitre 5. Applications de l’équation de Friedmann
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
T
Y
L
PO
N
H
EC
E
U
IQ
Fig. 5.1: L’âge de l’univers, t0 , en fonction de ΩM et ΩΛ . La région en bas à droite(t0 <
0.5tH ) est exclue car pour ces valeurs de ΩM et ΩΛ l’âge calculé est plus faible que l’âge
estimé des plus anciens amas globulaires de la Voie Lactée (∼ 1010 an). (Nous utilisons
H0 = 50 km s−1 Mpc−1 pour une limite supérieure sur tH .) La région en haut à gauche
(t0 = ∞) est exclue car pour ces valeurs de ΩM et ΩΛ il y a un minimum du paramètre
d’échelle, amin , qui correspond à l’annulation de ȧ. La solution de l’équation de Friedmann
pour ces valeurs est un univers primordial en contraction suivi d’un « rebond » à amin puis
de l’époque d’expansion actuelle. Le reshift maximum que cela implique zmax + 1 = a0 /amin
est en général en conﬂit avec les grands redshifts observés pour les galaxies et les quasars.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
L’âge de l’univers
T
Y
L
PO
N
H
EC
E
U
IQ
193
On voit également que l’âge est une fonction croissante de ΩΛ . Cela parce qu’une
énergie du vide positive accélère l’expansion ce qui implique une valeur plus faible de
ȧ dans le passé et par conséquent plus de temps pour aller de a = 0 à a = a0 .
Deux régions de l’espace (ΩΛ , ΩM ) peuvent être éliminées parce qu’elles mènent
à des âges incompatibles avec l’observation. La première qui peut être éliminée est
en haut à gauche dans la ﬁgure 5.1 notée t0 = ∞. Cette région est caractérisée par
des valeurs grandes et positives de ΩΛ ce qui implique une grande accélération de
l’expansion. Une accélération suﬃsamment grande impliquerait que ȧ se soit annulé
à un certain moment dans le passé. Dans ce cas, l’univers a commencé par une phase
de contraction (de durée peut-être inﬁnie) puis a « rebondi » à amin lorsque ȧ = 0. Le
rebond a été le commencement de l’époque actuelle d’expansion. Par exemple, dans
le cas ΩM ∼ 0, (5.4) nous dit que
ÉC
E
L
O
Å
âmin =
ΩΛ − 1
ΩΛ
ã1/2
ΩM ∼ 0 .
N
H
EC
E
U
IQ
(5.15)
Le rebond se produit si ΩΛ > 1.
L’existence de amin implique un redshift maximum zmax + 1 = a0 /amin . Si nous
demandons que zmax > 5 (le redshift maximum observé sur les quasars) cela élimine
la plus grande partie de la région (t0 = ∞) dans la ﬁgure 5.1. Pour ΩM ∼ 0, on a
E
L
O
T
Y
L
PO
ΩΛ < 1
ΩM ∼ 0 .
(5.16)
La seconde région de l’espace (ΩM , ΩΛ ) que l’on peut exclure est celle en bas à
droite (t0 < 0.5tH ) de la ﬁgure 5.1 où l’âge calculé est inférieur à celui des étoiles
les plus anciennes de la Voie Lactée. Parmi les plus anciennes, [118] il y a celles
contenues dans certains amas globulaires (d’étoiles) dans le halo de la Voie Lactée.
L’âge de ces étoiles peut être estimé à partir du diagramme couleur-magnitude (Fig.
5.2). L’estimation de l’âge des amas les plus anciens comme celui des naines blanches
les plus anciennes donne une limite inférieure de ∼ 1010 an pour l’âge de la Voie
Lactée.
La région de l’espace (ΩΛ , ΩM ) éliminée par les contraintes d’âge minimum dépend
de la valeur de H0 . Si l’on était certain que h70 > 1 on pourrait éliminer la région en
dessous de la ligne t0 = 0.67H0−1 y compris le point très intéressant ΩM = ΩT = 1
(5.13). Il serait plus conservateur de supposer que h70 > 0.7 dans quel cas, on ne peut
éliminer que la région au dessolus de la ligne t0 = 0.5 H0−1 .
En résumé, on voit qu’en imposant t0 > 1010 an et zmax > 5 on se limite à une
bande diagonale dans le plan ΩM , ΩΛ (Fig. 5.1). Nous verrons dans la section suivante
que des contraintes plus fortes viennent des distances angulaires et de luminiosité.
Même si la contrainte d’âge n’est pas très forte à l’heure actuelle, elle a eu une inﬂuence considérable sur l’histoire de la cosmologie. Initialement, Hubble avait mesuré
un taux d’expansion plus d’un ordre de grandeur supérieur à la valeur actuelle. (Les
« Céphéides » qu’il avait identiﬁées étaient en réalité d’autres étoiles plus brillantes
ce qui lui faisait sous-estimer les distances galactiques.) Cela donnait un temps de
Hubble de l’ordre de tH ∼ 109 an, signiﬁcativement inférieur à l’âge de la Terre, que
ÉC
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
194
ÉC
E
U
IQ
Chapitre 5. Applications de l’équation de Friedmann
E
L
O
T
Y
L
PO
N
H
EC
Z=2E−4 Y=0.23
E(B−V)=0.06 DM=15.30
14.0
M68
15.0
16.0
V
17.0
18.0
10 Gyr
11
12
19.0
20.0
21.0
22.0
−0.2
ÉC
E
L
O
T
Y
L
PO
0.0
0.2
0.4
B−V
N
H
EC
0.6
E
U
IQ
0.8
Fig. 5.2: Le diagramme couleur-magnitude de l’amas globulaire M68. Les amas globulaires
sont des amas d’étoiles contenant ∼ 105 membres que l’on trouve autour des disques galactiques, dans les halos. Le diagramme montre la séquence principale le long de la diagonale qui
commence à (B − V = 0.8, V = 22) et qui se termine abruptement à (B − V = 0.4, V = 19).
Cela contraste avec celui des étoiles proches vues par Hipparcos (ﬁgure 2.3) où la séquence
principale continue vers les plus petites valeurs de B −V et des magnitudes plus brillantes. Le
manque d’étoiles brillantes, bleues et massives sur la partie supérieure de la séquence principale de M68 provient de ce que de telles étoiles ont des durées de vie plus courtes que celle des
étoiles peu brillantes, rouges et peu massives de la partie inférieure de la séquence principale.
(L ∝ M 3 → τ ∝ M −2 , exercice 2.10.) Les étoiles de la partie supérieure de la séquence
principales qui étaient présentes lorsque M68 s’est formée ont, depuis, quitté la séquence
principale pour évoluer en géantes rouges et en naines blanches. Les trois courbes montrent
la position calculée des étoiles les plus brillantes de la séquence principale (le « coude » de
la séquence principale) pour des âges de M68 de 10, 11 et 12 milliards d’années. La position
calculée du coude est en accord avec les observations pour un âge de 11 milliards d’années
[119]. Document de A. Weiss.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Distances de luminosité et distances angulaires
T
Y
L
PO
N
H
EC
E
U
IQ
195
l’on connaissait par datation radioactive. Ce conﬂit était une source d’inspiration pour
les tenants de « modèles d’univers stationnaires » parmi lesquels Fred Hoyle, disparu
pendant l’été 2001. À l’origine, de tels modèles faisaient l’hypothèse d’une création
permanente de matière de façon à garder une densité d’énergie constante. Ces modèles
sont dynamiquement équivalents à des univers dominés par le vide et donnent un âge
inﬁni pour l’univers si la densité d’énergie est véritablement constante.
De meilleures estimations de H0 ont éliminé cette raison d’être pour les modèles
stationnaires. Le fait que les étoiles les plus anciennes aient un âge de l’ordre de tH
est un argument très fort contre le modèle stationnaire puisque dans ce modèle on
s’attendrait à voir des étoiles beaucoup plus anciennes. Dans la cosmologie standard,
les premières étoiles se forment à peu près 109 an après le big bang. Il est encourageant
que l’âge estimé des plus anciens amas globulaires de la Voie Lactée (∼ 1.1 × 1010 an)
soit de quelques 109 ans inférieur à l’âge estimé de l’univers (5.14) pour les valeurs
actuellement préférées de (ΩM , ΩΛ ).
Enﬁn, notons que le calcul de l’âge de l’univers suppose que rien d’inattendu ne
se produit pour a → 0. Puisque nous ne connaissons pas la physique aux premiers
instants (températures élevées) on ne peut pas justiﬁer cette hypothèse. Il est facile de
penser à des moyens de modiﬁer ρ(a) pour a → 0 de façon à accroître signiﬁcativement
l’âge. On peut le voir sur l’expression générale de t(a) :
a0
da
t0 =
.
(5.17)
1/2
0
a ( 8πGρ(a)/3 + H02 (1 − ΩT )â−2 )
ÉC
E
L
O
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
Par exemple, l’intégrale diverge si ΩT = 1 et ρ(a) → constante pour a → 0. Ce
peut être le cas dans des modèles inﬂationnaires. Pour cette raison, il est préférable
de nommer « âge de l’univers » le temps écoulé depuis l’époque où s’applique la
physique connue, par exemple depuis T ∼ MeV.
2
Distances de luminosité et distances angulaires
Dans la section 5, nous avons montré que la coordonnée radiale χ1 d’un objet de
redshift z est donnée par :
a0
da
χ1 (z) =
a0 /(1+z) aȧ
∼
dH
a0
1
dâ
(1+z)−1
â2
(ΩM
â−3
H
C
E
+ ΩΛ + (1 − ΩM − ΩΛ )â−2 )
T
Y
POL
1/2
,
U
Q
I
N
(5.18)
où, dans la deuxième forme, nous négligeons ΩR . Pour des objets proches (distances
dH ⇒ z 1) nous avons déjà vu (3.61) que cela se réduit à
ï
ò
1 + q0
z + ......
z1,
(5.19)
a0 χ1 (z) ∼ z dH 1 −
2
ÉC
E
L
O
E
196
E
U
IQ
Chapitre 5. Applications de l’équation de Friedmann
T
Y
L
PO
où le paramètre de décélération q0 est
q0 =
E
L
O
N
H
EC
ΩM
− ΩΛ .
2
(5.20)
Le terme d’ordre zéro dans (5.19) a0 χ1 (z) = H0−1 cz est simplement une expression de
la loi de Hubble, c’est-à-dire que la vitesse cz est proportionnelle à la distance a0 χ.
La première correction à la loi de Hubble dépend de q0 essentiellement pour la même
raison que l’âge de l’univers dépend de la décélération. Un redshift donné correspond
à un facteur d’expansion ﬁxe a0 /a1 entre l’émission et l’absorption. La décélération
implique une expansion rapide (dans le passé) ce qui diminue le temps d’expansion
et, par conséquent, le temps de vol des photons. Un temps de vol diminué implique
une distance comobile plus courte χ1 entre la source et l’observateur (Fig. 3.10).
La distance a0 χ1 est, bien entendu, non mesurable à l’heure actuelle. Plus importante est la distance de luminosité a0 r1 (1 + z) et la distance angulaire a0 r1 /(1 + z).
Le ﬂux d’énergie φ d’une source de redshift z et de luminosité L est
ÉC
φ =
L
.
4πd2L
T
Y
L
PO
N
H
EC
E
U
IQ
(5.21)
Pour les sources proches, r ∼ χ (à l’ordre z 2 ) ce qui donne
E
L
O
φ =
ÉC
L
(1 + (q0 − 1)z + .....)
4πd2H z 2
z1.
(5.22)
La dépendance en z de φ pour une chandelle standard peut ainsi être utilisée pour
estimer q0 . Une grande décélération implique un grand ﬂux puisque dans ce cas la
distance entre la source et l’observateur est petite.
Deux groupes, le Supernova Cosmology Project [26] et le High-Z Supernova Search
[27] ont présenté des diagrammes de Hubble de supernovae de grand redshift qui
peuvent être interprétés comme un argument expérimental en faveur d’un q0 négatif,
c’est-à-dire en faveur d’un univers en accélération. Le diagramme de Hubble est montré
sur la ﬁgure 5.3. En moyenne, les supernovae à z ∼ 0.5 sont de 0.2 mag (20%)
moins lumineuses que ce que l’on attendrait d’un univers de basse densité (ΩM =
0.3, ΩΛ = 0) et moins lumineuses de 0.4 mag pour un univers (ΩM = 1, ΩΛ = 0).
Trois explications viennent à l’esprit :
U
Q
I
N
– La luminosité moyenne des supernovae était plus faible dans le passé, peutêtre parce que les abondances des diﬀérents éléments pré-séquence principale
ont mené à une distribution diﬀérente de masses ou d’abondances des éléments
avant l’explosion.
Y
L
PO
H
C
TE
– 20% de la lumière de la supernova est absorbée quelque part entre la supernova
et la Terre. L’absorption doit être à peu près indépendante de la longueur d’onde
car la forme des spectres observés de grand redshift est pratiquement identique
à celle des supernovae proches.
ÉC
– q0 est négatif.
E
L
O
E
Distances de luminosité et distances angulaires
E
L
O 42
ÉC
m-M (mag)
44
T
Y
L
PO
197
Riess et al. 1998
Perlmutter et al. 1999
40
38
ΩM=0.3, ΩΛ=0.7
36
ΩM=0.3, ΩΛ=0.0
34
ΩM=1.0, ΩΛ=0.0
1.5
∆(m-M) (mag)
N
H
EC
E
U
IQ
1.0
E
L
É C0.0O
0.5
T
Y
L
PO
N
H
EC
E
U
IQ
-0.5
-1.0
-1.5
0.01
0.10
z
1.00
U
Q
I
N
Fig. 5.3: Mesures de luminosités apparentes de supernovae de type Ia par le Supernova
H
C
TE
Cosmology Project [26] et le High-Z Supernova Search [27]. (compilation due à A. Riess
[120]). Le panneau supérieur montre le diagramme de Hubble. Le panneau inférieur montre
la diﬀérence entre les magnitudes apparents observées et la magnitude attendue pour un
univers avec (ΩM = 0.3, ΩΛ = 0.0). À z ∼ 0.5, les supernovae sont en moyenne ∼ 0.2 mag
(20%) moins lumineuses que ce que l’on attend pour (ΩM = 0.3, ΩΛ = 0.0). Cet eﬀet peut
s’expliquer en supposant que (ΩM ∼ 0.3, ΩΛ ∼ 0.7).
ÉC
E
L
O
Y
L
PO
E
198
E
U
IQ
Chapitre 5. Applications de l’équation de Friedmann
T
Y
L
PO
N
H
EC
La première hypothèse est diﬃcile à rejeter complètement mais elle peut être
analysée en étudiant des supernovae proches dans des galaxies d’âge diﬀérent (par
exemple les abondances diﬀérentes d’éléments lourds).
La deuxième hypothèse suppose l’existence d’un poussière absorbante avec des
caractéristiques diﬀérentes de la poussière de la Voie Lactée (qui mène à un rougissement des spectres). La poussière réémettrait nécessairement de la lumière stellaire
dans l’infra-rouge ce qui créerait un fond anisotrope dans l’infra-rouge. La limite présente sur le fond diﬀus n’est pas suﬃsamment forte pour éliminer la possibilité de
l’existence de la quantité voulue de poussière [105]
Si l’on suppose que l’eﬀet est dû à une accélération cosmique, la région permise
dans l’espace (ΩM , ΩΛ ) est montrée sur la ﬁgure 5.4. Les lignes de probab ilité sont
orientées suivant la direction de 0.8ΩM − 0.6ΩΛ constant, quelque peu à l’oblique des
lignes de q0 = ΩM /2 − ΩΛ constant car à un redshift de z ∼ 0.5 (5.22) n’est pas
une approximation particulièrement bonne. On voit que si ΩM > 0, ΩΛ > 0 avec un
niveau de conﬁance de 95%. Si l’on adopte ΩM ∼ 0.3 comme c’est suggéré par l’étude
des amas de galaxies, cela implique une valeur de ΩΛ
ÉC
E
L
O
ΩΛ ∼ 0.7
⇒ q0 ∼ −0.55
T
Y
L
PO
N
H
EC
(si ΩM ∼ 0.3) .
E
U
IQ
(5.23)
Insistons sur le fait que ce résultat remarquable suppose que les supernovae de
grand redshift ont la même distribution en luminosité que les supernovae voisines et
qu’il n’y a pas d’absorption signiﬁcative.
Avant les résultats sur les supernovae, les contraintes les plus fortes sur ΩΛ venaient
de recherches sur les quasars de grand redshift qui ont deux images causées par les
amas de galaxies au premier plan. Comme nous l’avons vu au chapitre 3, section 8,
la probabilité de déviation des rayons lumineux (3.102) est une fonction croissante de
la distance quasar-observateur. Sans aller dans le détail du calcul de la probabilité
dans une métrique de Robertson-Walker, il n’est pas surprenant que la probabilité
soit une fonction croissante de a0 χ1 et par conséquent une fonction décroissante de
q0 . La probabilité observée pour le lensing [121] est en accord avec ce que l’on attend
d’un univers ΩT = ΩM = 1. Le taux donne une limite supérieure ΩΛ < 0.7 avec un
degré de conﬁance de 90%. Ce résultat n’est que marginalement en accord avec les
mesures de q0 qui utilisent les supernovae de type Ia.
Au vu des résultats du lensing gravitationnel, il est particulièrement important
d’avoir des observations qui conﬁrment l’hypothèse que q0 est négatif. Trois possibilités supplémentaires pour mesurer q0 sont le comptage du nombre des galaxies
(exercice 5.5), le diagramme de Hubble d’amas de galaxies en utilisant l’eﬀet SunyaevZel’dovich (exercice 5.6), et le diagramme de Hubble des supernovae de type II en
utilisant la méthode de la photosphère en expansion (exercice 5.7).
Enﬁn, notons qu’il sera peut-être possible un jour de mesurer directement la décélération de l’univers en observant la dépendance en temps du redshift des objets
distants [122]. De telles mesures demanderaient des mesures extrêmemnt précises du
redshift sur des durées longues.
ÉC
E
L
O
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
De l’information complémentaire sur (ΩM , ΩΛ ) peut être obtenue à partir d’objets
E
Distances de luminosité et distances angulaires
ÉC
E
L
O1.0
T
Y
L
PO
N
H
EC
E
U
IQ
199
age=1.00/Ho
0.90/Ho
0.8
Ωo=1
0.80/Ho
0.6
ΩΛ
0.4
SN1a
É0.2C
E
L
O
T
Y
L
PO
N
H
EC
0.75/Ho
CMB
0.2
0.4
0.70/Ho
0.67/Ho
185 < lpeak < 209
0.0
0.0
E
U
IQ
0.6
0.8
1.0
Ωm
U
Q
I
N
Fig. 5.4: Les plages permises pour ΩM et ΩΛ d’après le diagramme de Hubble des supernovae
de type Ia (petits points) [26, 27] et d’après la mesure de Boomerang [106] du premier pic
acoustique dans le spectre des anisotropies du CBR (gros points). Dans les deux cas, le régions
ombrées correspondent au niveau de conﬁance de 95%. Les résultats combinés sont en faveur
de valeurs proches de ΩΛ ∼ 0.7 et ΩM ∼ 0.3. Également représentés, les contours de l’âge de
l’univers et la ligne ΩT = 1(= Ω0 ).
ÉC
E
L
O
Y
L
PO
H
C
TE
E
200
E
U
IQ
Chapitre 5. Applications de l’équation de Friedmann
N
H
EC
de très grand redshift z 1. Pour ΩM = ΩT = 1 on calcule facilement
T
Y
L
PO
lim a0 χ1 (z) = 2H0−1
E
L
O
ΩM = ΩT = 1 .
z→∞
(5.24)
Pour ΩM petit, l’intégrale pour χ1 diverge logarithmiquement jusqu’à ce qu’elle soit
coupée à â ∼ ΩM :
ÉC
lim a0 χ1 (z) ∼ H0−1 ln(4/ΩM )
ΩM = ΩT 1 .
z→∞
(5.25)
Comme on s’y attend, a0 χ1 croît lorsque ΩM décroît à cause de l’eﬀet de décélération
déjà vu en (5.19).
Pour les distance de luminosité et les distance angulaires nous avons besoin de
r = sinh−1 χ qui ampliﬁe la dépendance en ΩM . Dans le cas ΩΛ = 0, le résultat,
calculé dans l’exercice 5.10, est :
lim a0 r1 =
z→∞
2H0−1
ΩM
N
H
EC
(ΩΛ = 0) .
E
U
IQ
(5.26)
Il n’y a pas d’objets à z 1 qui peuvent constituer des chandelles standard (ou
des mètres standard). Toutefois, nous verrons dans le chapitre 7 que le CBR a un
spectre d’anisotropies qui dépend de l’échelle angulaire, c’est-à-dire de la taille des
pixels utilisés pour mesurer les variations de température. Plus précisément, notons
T (
θ, ∆θ) la température observée dans la direction θ et moyennée sur un disque de
rayon ∆θ dans le ciel. La variance de cette quantité sur toutes les directions est
ã
Å
1
2
dΩ T (θ, ∆θ)2 − T 2 .
=
(5.27)
∆T∆θ
4π
ÉC
E
L
O
T
Y
L
PO
Les observations décrites au chapitre 7 montrent un pic de cette quantité près de
∆θ ∼ 1 deg (Fig. 7.10).
D’après une classe en vogue de modèles de formation de structures (modèles de
CDM avec des ﬂuctuations primordiales adiabatiques et invariantes d’échelle, voir le
chapitre 7), la taille de l’échelle où l’on s’attend à voir les plus grandes ﬂuctuations
est celle qui correspond à la distance de Hubble à la recombinaison (ârec ∼ 1/1100).
Cette distance est donnée par l’équation de Friedmann (5.4). L’univers était dominé
par la matière à la recombinaison (trec > teq ) ce qui implique
dH (arec ) =
H0−1
1/2 3/2
ΩM zrec
,
T
Y
POL
H
C
E
U
Q
I
N
(5.28)
où zrec ∼ 1/ârec ∼ 1100. La distance angulaire est a0 χ1 /(1 + z) et en utilisant (5.26)
on trouve la taille angulaire correspondante
θH (zrec ) =
E
L
O
dH (zrec )
∼ 0.015 rad ΩM
dA (zrec )
ÉC
(ΩΛ = 0) .
(5.29)
E
Distances de luminosité et distances angulaires
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
T
Y
L
PO
E
U
IQ
N
H
EC
201
E
U
IQ
Fig. 5.5: Taille angulaire de la distance de Hubble à la recombinaison, θH (zrec ), et paramètre
de décélération, q0 = ΩM /2 − ΩΛ , en fonction de ΩM et ΩΛ . Le diagramme de Hubble pour
les supernovae de type Ia peut être utilisé pour déterminer q0 et les anisotropies du spectre du
CBR peuvent être utilisées pour déterminer θH . Parce que les contours des deux grandeurs
sont pratiquement orthogonaux, en combinant les mesures de q0 et de θH , il est possible de
déterminer avec précision ΩM et ΩΛ , comme sur la ﬁgure 5.4.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
202
E
U
IQ
Chapitre 5. Applications de l’équation de Friedmann
N
H
EC
Pour ΩΛ = 0, θH (zrec ) peut être calculé numériquement (ﬁgure 5.5). Nous remarquons
que si ΩT = 1, θH (zrec ) est presque indépendant des valeurs relatives de ΩM et ΩΛ
(exercice 5.11) :
ÉC
E
L
O
T
Y
L
PO
θH (zrec ) ∼ 0.015
ΩT = 1 .
(5.30)
La valeur de θH prévue pour ΩT = 1 est en bon accord avec la valeur observée par les
expériences Boomerang et Maxima (Fig. 7.10). Les résultats combinés donnent [25] :
ΩT = 1.11 ± 0.07 .
(5.31)
Nous remarquons que les lignes de θH (zrec ) constant sont pratiquement orthogonales aux lignes de q0 constant. Les résultats de l’anisotropie du CBR peuvent donc
être combinés avec ceux des supernovae de type Ia pour contraindre étroitement ΩM
et ΩΛ , comme on le voit sur la ﬁgure 5.4. Les résultats combinés sont [25] :
ΩM ∼ 0.34 ± 0.1
C
E
T
LY
ΩΛ ∼ 0.75 ± 0.1 .
HN
E
U
IQ
(5.32)
(5.33)
O
P
E
L
O
ÉLeCproblème
de l’horizon
La valeur déduite pour ΩM est compatible avec celle estimée à partir de la fraction
baryonique dans les amas de galaxies (Sect. 5) et de l’étude des inhomogénéités de
densité (Sect. 6).
3
Les objets les plus lontains qu’il serait concevable de voir auraient un redshift
inﬁni, c’est à dire que les photons que nous détecterions aujourd’hui auraient été émis à
a = 0. Il est intéressant de remarquer que pour un univers dominé par le rayonnement
ou par la matière, la distance de ces objets est ﬁnie, c’est-à-dire que l’intégrale (5.18)
pour χ(z) ne diverge pas pour z → ∞. Si l’intégrand représente bien les conditions
pour a → 0, on peut donc en déduire l’existence d’un « horizon » qui donne la
coordonnée radiale des points les plus lointains qui peuvent avoir communiqué avec
nous depuis le big bang :
χhor =
dH
a0
0
1
dâ
â2
(ΩM
â−3
H
C
E
1/2
+ ΩΛ + (1 − ΩT )â−2 )
T
Y
POL
.
U
Q
I
N
(5.34)
Les photons émis aux points χ > χhor ne nous ont pas encore atteints. La distance
actuelle de l’horizon, a0 χhor , est de l’ordre de dH . Pour ΩM = ΩT = 1 l’intégrale
(5.34) donne a0 χhor = 2dH .
L’existence d’un horizon est peut-être surprenante au vu du fait que des observateurs comobiles sont séparés par des distances qui sont proportionnelles à a(t) et qui
ÉC
E
L
O
E
Le problème de l’horizon
N
H
EC
E
U
IQ
203
s’annulent donc au big bang.1 Toutefois, l’âge de l’univers s’annule encore plus vite,
t ∝ a2 pour t < teq . il s’ensuit que
ÉC
E
L
O
T
Y
L
PO
distance
∝ a−1 ,
temps disponible
(5.35)
et les observateurs comobiles sont complètement isolés pour a → 0.
Bien que les distances soient faibles, les photons émis hors du rayon de Hubble
ne peuvent pas atteindre l’origine rapidement. L’équation du mouvement des photons
dχ/dt = −1/a(t) implique que la distance aχ d’un photon qui se propage vers l’origine
obéit à l’équation
d(aχ)
aχ
=
−1.
dt
dH (t)
(5.36)
E
U
IQ
Un photon se dirigeant vers l’origine à une distance supérieure à la distance de Hubble,
(aχ > dH (t), voit sa distance à l’origine augmenter initialement. La distance ne décroît
que lorsque le dH rattrape aχ quand la particule arrive en deçà du rayon de Hubble.
(Voir l’exercice 4.7 pour une discussion plus approfondie de cette question).
L’horizon à un temps arbitraire t est donné par la généralisation de (5.34)
dH
χhor (a) =
a0
ÉC
E
L
O
T
Y
L
PO
0
a/a0
â2
(ΩM
â−3
N
H
EC
dâ
+ ΩΛ + (1 − ΩT )â−2 )1/2
.
(5.37)
Puisqu’il n’y a rien de particulier avec l’époque actuelle, il n’est pas surprenant que
cette intégrale donne une distance de l’horizon de l’ordre de la distance de Hubble à
l’époque considérée. De l’équation de Friedmann on sait que dH ∝ a2 pour a < aeq et
dH ∝ a3/2 pour aeq < a < acΛ . Il s’ensuit que
χhor (a) ∝ a
χhor (a) ∝ a1/2
a < aeq
(5.38)
aeq < a < acΛ .
(5.39)
L’évolution de l’horizon avec le temps est illustrée sur la ﬁgure 5.6 qui montre les
trajectoires χ(t) des photons passant par l’origine χ = 0.
L’existence d’un horizon nous met en présence d’un paradoxe en ce qui concerne
l’uniformité du CBR. À trec l’horizon était de l’ordre de la distance de Hubble à
cette époque, arec χhor (arec ) ∼ dH (arec ). Comme nous l’avons vu dans la section
précédente, cela correspond à un angle dans le ciel d’à peu près 1 degré si ΩT ∼ 1.
Comme l’illustre la ﬁgure 5.7, des points séparés par des angles supérieurs n’avaient
pas communiqué avant trec . L’uniformité du CBR est donc un mystère puisque aucun
mécanisme causal, par exemple la diﬀusion de chaleur, ne pouvait avoir rendu la
température uniforme.
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
1 Bien que cela soit vrai, il faut se rappeler que le volume d’un univers homogène avec Ω ≤ 1 est
T
inﬁni pour toute valeur de a > 0.
ÉC
E
204
ÉC
E
U
IQ
Chapitre 5. Applications de l’équation de Friedmann
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
T
Y
L
PO
N
H
EC
E
U
IQ
Fig. 5.6: Trajectoires de photons χ(t) qui commencent au big bang et passent par l’origine
χ = 0 (en supposant que l’univers est transparent). Les trajectoires sont calculées
pour un
−1
H
a(t)/a0 .
univers ΩT = ΩM = 1, a(t) ∝ t2/3 ce qui implique que χ(t) = χ(t = 0) − 2a−1
0
0
Le temps (axe vertical) est paramétrisé par a(t)/a0 . La trajectoire χ(t) (axe horizontal) est
multipliée par a0 H0 . On voit qu’un photon émis en un point comobile actuellement à une
distance χa0 = 2H0−1 atteint l’origine aujourd’hui (a(t)/a0 = 1). Cela signiﬁe que notre
horizon est à une distance de 2H0−1 . Quand le temps croît, un observateur à χ = 0 voit des
photons arriver de points comobiles de plus en plus lointains.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Le problème de l’horizon
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
205
χ( zrec )
χ=0
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
horizon
Fig. 5.7: Deux points sur la surface χ = χ(zrec ) avec leur horizon à trec . Des paires de
points séparés par plus de ∼ 1degré dans le ciel étaient hors de l’horizon l’un de l’autre. La
quasi-égalité de la température des deux points ne peut pas provenir d’un processus causal
comme la diﬀusion de la chaleur.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
206
E
U
IQ
Chapitre 5. Applications de l’équation de Friedmann
T
Y
L
PO
N
H
EC
Il y a deux réponses à ce mystère. La première est de dire que les conditions
initiales étaient telles que la température était uniforme. Ça pourrait être équivalent
de dire que la température initial était ﬁxée par les « lois de la physique » ou peut-être
qu’elle n’a rien à voir avec la physique.
La seconde, plus à la mode, est de modiﬁer la densité d’énergie ρ(a) dans la limite
a → 0 de telle façon qu’on accroisse χhor considérablement. Un exemple simple serait
de supposer ρ(a) = constant pour a2 < a < a1 aeq comme le montre la ﬁgure
5.8. Il est équivalent de supposer que pour a2 < a < a1 l’univers est dominé par une
énergie du vide qui se transforme d’une certaine façon en rayonnement à a1 . C’est
plus ou moins ce qui se passe dans les modèles inﬂationnaires que nous discuterons
dans la section 5. Puisque l’évolution de ρ n’est plus décrite par un simple mélange
de particules et de vide, on doit revenir à l’expression générale de χ(z)
ÉC
E
L
O
a0
χhor =
0
da
=
aȧ
a0
0
da
a2
E
U
IQ
1/2
(8πGρ/3 + H02 (1 − ΩT ) â−2 )
N
H
EC
.
(5.40)
Si la densité d’énergie est constante pour a2 < a < a1 , cette expression diverge pour
a2 → 0. On peut donc résoudre formellement le problème de l’horizon avec ce « tour
de passe-passe ». La raison en est que pendant l’époque de domination par une densité
d’énergie constante, l’univers se dilate exponentiellement avec un temps de Hubble
constant H1−1 pour a2 < a < a1 :
ÉC
E
L
O
T
Y
L
PO
a(t) = a2 exp H1 (t − t2 )
H12 ∼
8πGρ(a1 )
.
3
(5.41)
L’univers passe un temps de Hubble H1−1 avec a ∼ a2 . Si l’univers avait été dominé
par le rayonnement pour a2 < a < a1 , Il aurait passé un temps considérablement
plus court avec a ∼ a2 : H2−1 ∼ H1−1 a22 /a21 . L’augmentation de temps passé pendant
que l’univers était « petit » permet une communication sur de plus grandes distances
comobiles. Ceci est illutré sur la ﬁgure 5.9.
Nous discuterons des modèles inﬂationnaires en plus grand détail dans la section 5.
Sans en connaître le détail, on peut facilement estimer la durée nécessaire de l’inﬂation
dont on a besoin pour résoudre le problème de l’horizon. Pendant l’inﬂation, l’horizon
est
t
ó
1
1 î
dt
1 − e−H1 (t−t2 ) ∼
∼
,
(5.42)
χhor (t) ∼
H1 a 2
H1 a 2
t2 a(t)
H
C
TE
U
Q
I
N
où nous avons négligé la période qui précède l’inﬂation. On voit que l’horizon est
essentiellement ﬁxé au début de l’inﬂation lorsque les distances entre points comobiles sont les plus courtes. Pour résoudre le problème de l’horizon, nous voulons que
l’horizon pendant l’inﬂation inclue le volume de Hubble actuel :
ÉC
E
L
O
Y
L
PO
a0 χhor (t ∼ t2 ) > H0−1 .
(5.43)
E
Le problème de l’horizon
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
207
ρ =constant
log ρ
ρ
ÉC
E
L
O
a2
a−4
T
Y
L
PO
a1
N
H
EC
aeq
ρ
E
U
IQ
a−3
log a
Fig. 5.8: La densité d’énergie ρ(a) dans un scénario inﬂationnaire simple. Les époques de
matière et de rayonnement sont précédées par une époque inﬂationnaire a2 < a < a1 quand
l’univers est dominé par une énergie eﬀective du vide. À la ﬁn de l’inﬂation, cette énergie
doit être partiellement transformée en rayonnement, ce qui donne les conditions initiales
pour la cosmologie classique. Ce processus sera décrit dans la section 5.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
208
ÉC
E
U
IQ
Chapitre 5. Applications de l’équation de Friedmann
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
T
Y
L
PO
N
H
EC
E
U
IQ
Fig. 5.9: Trajectoires de photons χ(t) comme dans la ﬁgure 5.6 sauf que l’univers est dominé par le vide (ρ = constant) pendant une époque inﬂationnaire a(t)/a0 < 10−5 . (Dans des
modèles inﬂationnaires plus réalistes, l’époque inﬂationnaire prend ﬁn après l’époque GUT
-grande uniﬁcation- a(t)/a0 ∼ 10−28 , T ∼ 1015 GeV). Pendant l’époque de matière, les trois
trajectoires A, B et C suivent les trois trajectoires de la ﬁgure 5.6. À la ﬁn de l’inﬂation, la
trajectoire A passe par l’horizon classique à une distance actuelle de 2H0−1 . Pendant l’époque
inﬂationnaire, les courbes continuent vers la droite, ce qui augmente considérablement l’horizon. C’est dû à l’augmentation du temps que l’univers passe à petit a(t). Notons (trajectoire
D) que le point χ = 0 était, à la ﬁn de l’inﬂation, déjà capable de communiquer avec l’intégralité de l’horizon classique si l’inﬂation a commencé avant a(t)/a0 = 10−8 .
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Le problème de l’horizon
T
Y
L
PO
En utilisant (5.42) cela devient
E
L
O
N
H
EC
E
U
IQ
a0 a1 −1
H
> H0−1 .
a1 a2 1
209
(5.44)
Mais, en utilisant l’équation de Friedmann et en négligeant la courbure on a
ÉC
H12 ∼
ρ1 2
ρR (t0 ) a40 2
H0 ∼
H .
ρ0
ρM (t0 ) a41 0
(5.45)
(Nous négligeons les eﬀets provenant des changements du nombre de degrés de liberté, comme nous le verrons au chapitre 6.) En prenant ρR (t0 )/ρM (t0 ) ∼ 10−4 et en
substituant dans (5.44) on trouve que pour résoudre le problème de l’horizon on doit
avoir
a0
a1
> 10−2
,
(5.46)
a2
a1
N
H
EC
E
U
IQ
c’est-à-dire que l’expansion pendant l’inﬂation doit être au moins 1 % de l’expansion
après l’inﬂation.
Le succès de la théorie de la nucléosynthèse primordiale nous dit que l’inﬂation
ne peut pas s’être produite après T ∼ MeV. On suppose souvent que l’inﬂation a
aﬀaire avec les interactions des théories de Grande Uniﬁcation de la physique des
particules. Cela suggère que l’inﬂation s’est passée un peu après l’échelle de GUT,
T1 ∼ 1015 GeV, ce qui implique a0 /a1 ∼ 1028 . (On pense que l’inﬂation se produit au
dessous de l’échelle de GUT de façon à se débarasser de certaines particules inobservées
(par exemple les monopôles magnétiques) qui sont créées à l’échelle de GUT. Bien
qu’il existe des modèles où l’inﬂation se produit à des échelles aussi basses que ∼ TeV,
nous utilisons l’échelle de GUT dans les estimations numériques et l’on s’aperçoit que
pour résoudre le problème de l’horizon il est nécessaire que
ÉC
E
L
O
T
Y
L
PO
a1
> 1026 ∼ e60
a2
si T1 ∼ 1015 GeV .
(5.47)
Les ∼ 60 temps de Hubble pendant l’inﬂation ne durent que ∼ 60H1−1 ∼ 10−34 s.
Pendant ce temps, le volume de Hubble actuel se dilate depuis une taille de ∼ 10−28 m
jusqu’à ∼ 10−2 m avant de passer dans les époques de rayonnement et de matière
jusqu’à sa taille actuelle de ∼ 1026 m.
Aﬁn d’avoir un volume de Hubble actuel raisonnablement uniforme, nous demandons que le volume original, connecté de façon causale, soit raisonnablement uniforme
lui aussi. La condition initiale arbitraire non-causale est ainsi remplacée par une condition arbitraire mais causale qui peut être expliquée à l’aide d’une physique que nous
ne connaisson pas encore. Il n’est pas exact que l’inﬂation produit nécessairement un
univers homogène, mais seulement que l’univers homogène observable peut s’être développé de façon causale. Dans le cas des modèles inﬂationnaires où l’énergie est due
à un champ scalaire, il est nécessaire que le champ soit bien approché par un champ
homogène classique, ce qui veut dire que le champ quantique correspondant est dans
son état fondamental.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
210
E
U
IQ
Chapitre 5. Applications de l’équation de Friedmann
T
Y
L
PO
N
H
EC
Les modèles inﬂationnaires augmentent considérablement notre véritable horizon
et nous pouvons nous interroger sur ce qu’est l’« horizon classique » que l’on calcule
en ignorant l’inﬂation. La réponse à cette question se trouve dans la ﬁgure 5.9 où l’on
voit qu’alors que nous pouvons recevoir des signaux de points au delà de l’horizon
classique, ils ont été envoyés à un temps où il n’y avait pas d’objets comme les étoiles,
les galaxies ou même les photons du CBR. L’horizon classique demeure donc l’horizon
pratique pour faire de l’astronomie.
Il est intéressant de voir ce qui se passera à l’horizon classique dans le futur. On
montre facilement (exercice 5.9) que l’horizon classique dans un univers ΩT = ΩM = 1
va continuer à croître avec le temps. En se reportant à la ﬁgure 5.6, on voit que les
trajectoires des photons balaieront des régions de plus en plus vastes quand le temps
augmente. Si l’on attend suﬃsamment, nous verrons tout.
D’un autre côté, nous verrons dans l’exercice 5.9 que dans un univers avec ΩΛ > 0,
χhor approche une limite ﬁnie pour t → ∞. L’expansion exponentielle dans un tel
univers ne laisse pas assez de temps aux photons pour nous atteindre depuis des objets
en récession rapide. On dit qu’un univers avec ΩΛ > 0 a un « horizon des événements »
au delà duquel nous ne pourrons jamais voir2. Cette situation est semblable à ce qui
se produit avec des trous noirs où on ne peut pas voir à l’intérieur du rayon de
Schwarzschild.
ÉC
4
E
L
O
T
Y
L
OΩ
Le problème des
P
E
L
ÉCO
N
H
EC
E
U
IQ
Le rapport entre la densité ρ(a) et la densité critique en fonction du paramètre
d’échelle est
ΩT (a) =
ρ(a)
,
3H 2 (a)/8πG
(5.48)
où H(a) = ȧ/a est donné par l’équation de Friedmann. Si ρ(a) est un mélange d’énergie relativiste, non-relativiste et d’énergie du vide, ceci devient
ΩT (a) =
ΩR â−4
ΩR â−4 + ΩM â−3 + ΩΛ
.
+ ΩM â−3 + ΩΛ + (1 − ΩT )â−2
Pour tout a a0 on trouve que ΩT s’approche de l’unité :
ΩT (a) = 1 −
1 − ΩT
â2
ΩR + ΩM â
â 1 .
H
C
TE
(5.49)
U
Q
I
N
(5.50)
Pendant l’époque de rayonnement, ΩT (a) − 1 est ainsi proportionnel au carré du
paramètre d’échelle. En extrapolant jusqu’à l’époque GUT , âGUT ∼ 10−28 on trouve
Y
L
PO
1 − ΩT (aGUT ) ∼
E
L
O
1 − ΩT (a0 ) 2
âGUT
ΩR (a0 )
2 Ce que nous avons appelé « horizon » est parfois nommé « horizon des particules » pour le
distinguer de l’horizon des événements.
ÉC
E
Le problème des Ω
N
H
EC
E
U
IQ
∼ 10−52 [1 − ΩT (a0 )] .
T
Y
L
PO
211
(5.51)
Puisqu’il doit être raisonnable d’aﬃrmer que |1−ΩT (a0 )| < 0.5, nous pouvons conclure
qu’à l’époque GUT, ce nombre était ajusté à 1 avec une précision de 52 chiﬀres après
la virgule !
La particularité de cette situation se comprend mieux en récrivant (5.51) en commençant à l’époque GUT. pendant l’époque du rayonnement, on a
ÉC
E
L
O
Å
[1 − ΩT (a)] ∼ [1 − ΩT (aGUT )]
a
ã2
.
aGUT
(5.52)
On
voit que ΩT commence à diﬀérer de 1 après une expansion de a/aGUT ∼
1/ |1 − ΩT (aGUT )|. Le fait que ΩT soit toujours voisin de 1 n’est donc possible
que si ΩT était très ﬁnement ajusté à 1 à l’époque GUT.
Il se trouve qu’une époque inﬂationnaire suﬃsamment longue pour résoudre le problème de de l’horizon va aussi maintenir ΩT suﬃsamment près de 1 pour satisfaire(5.51).
Pendant l’inﬂation, Ω évolue selon
ΩT (a) =
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
ΩT (a2 )
,
ΩT (a2 ) + (1 − ΩT (a2 ))(a/a2 )−2
(5.53)
où a2 est le début de l’inﬂation. On voit que pendant l’inﬂation ΩT → 1 pour a a2 .
À la ﬁn de l’inﬂation on a
ÉC
1 − ΩT (a1 ) ∼
1 − ΩT (a2 ) a22
.
ΩT (a2 ) a21
(5.54)
Aﬁn de résoudre le problème de l’horizon, a2 /a1 doit respecter les conditions (5.46)
ou (5.47) ce qui implique
|1 − ΩT (a1 )| <
|1 − ΩT (a2 )| −52
10
.
ΩT (a2 )
(5.55)
Le facteur 10−52 est exactement ce dont nous avons besoin ! En combinant cette
équation avec (5.51) et en posant a1 = aGUT , nous trouvons qu’aujourd’hui
|1 − ΩT (a0 )| =
|1 − ΩT (a2 )|
ΩT (a2 )
a22 /a21
10−52
<
|1 − ΩT (a2 )|
.
ΩT (a2 )
T
Y
POL
H
C
E
U
Q
I
N
(5.56)
On voit que ΩT doit être proche de 1 aujourd’hui sauf si ΩT (a2 ) était très petit.
Même si c’est toujours une condition non-triviale, le fait que ΩT soit proche de l’unité
aujourd’hui ne doit plus être considéré comme le résultat d’un ajustement extraordinairement ﬁn (ﬁne tuning) à l’époque GUT mais plutôt comme une contrainte
« raisonnable » sur les conditions du début de l’inﬂation et sur la durée de celle-ci.
ÉC
E
L
O
E
212
5
E
U
IQ
Chapitre 5. Applications de l’équation de Friedmann
L’inﬂation
T
Y
L
PO
N
H
EC
Nous venons de voir que le problème de l’horizon et le problème des Ω peuvent
trouver une solution si, pendant une époque suﬃsamment longue (a2 < a < a1 )
l’univers a eu une densité d’énergie à peu près constante comme sur la ﬁgure 5.8. Une
énergie constante ne peut pas provenir d’une simple constante cosmologique parce
qu’une partie de l’énergie doit être transformée en rayonnement à t1 . Les scénarios
inﬂationnaires donnent un mécanisme (ou au moins une équation diﬀérentielle) qui le
réalise.
Le scénario inﬂationiste original [123] proposé par Guth supposait que l’univers
était piégé dans un vide métastable dont il a échappé par eﬀet tunnel quantique
ou par ﬂuctuations thermiques. Ce scénario était bien appuyé par certaines théories
grand uniﬁées. Malheureusement, le processus d’eﬀet tunnel, qui est équivalent à une
transition de phase du premier ordre, engendre de grandes inhomogénéités pendant
le processus de nucléation.
La deuxième génération de modèles inﬂationnaires utilise des champs scalaires
pour créer une énergie du vide eﬀective. Nous avons vu dans la section 5 qu’un champ
scalaire φ caractérisé par un potentiel V (φ) peut simuler une énergie du vide si les
dérivées spatiales et temporelle sont suﬃsamment faibles, dans quel cas ρ ∼ V (φ) et
p ∼ −V (φ). Le champ est régi par (4.77)
ÉC
E
L
O
ÉC
E
L
O
T
Y
L
PO
φ̈ + 3
N
H
EC
E
U
IQ
ȧ
φ̇ + V (φ) = 0 .
a
(5.57)
Un exemple de potentiel qui peut donner une densité d’énergie comme celle de la
ﬁgure 5.8 est montré sur la ﬁgure 5.10. Des potentiels de ce type sont utilisés dans les
modèles de « nouvelle inﬂation » proposés par Linde et par Steinhardt et Albrecht
[124]. Le potentiel est caractérisé par une région plate pour φ2 < φ < φ1 suivie d’une
chute brusque dans un minimum situé à φ0 .
On suppose que l’inﬂation commence à a2 avec le champ à φ2 loin du minimum.
D’après (5.57), les champs « descendent » vers le minimum en atteignant une vitesse
ﬁnale de
φ̇ =
−V (φ)
3ȧ/a
a2 < a < a1 .
(5.58)
U
Q
I
N
Si cette vitesse est atteinte, on dit que la condition de « descente lente » est satisfaite.
Avant d’atteindre a1 , le potentiel est relativement plat et nous avons une inﬂation
presque parfaite :
ρ(a) ∼ V (φ) ∼ constante
Y
L
PO
H
C
TE
a 2 < a < a1 .
(5.59)
Après être tombé dans le puits de potentiel, le champ eﬀectue des oscillations amorties
autour du minimum jusqu’à s’y ﬁxer. Les oscillations sont amorties à cause du terme
φ̇ dans (5.57). Le rayonnement de particules peut être obtenu en couplant φ aux
champs de matière. Ce « réchauﬀement » de l’univers, comme on l’appelle, se décrit
ÉC
E
L
O
E
L’inﬂation
V (φ)
ÉC
E
L
O
T
Y
L
PO
φ2
N
H
EC
E
U
IQ
φ0
φ1
N
H
EC
213
E
U
IQ
φ
Fig. 5.10: Un potentiel inﬂationnaire qui produit une densité d’énergie semblable à celle
de la ﬁgure 5.8. Le champ est supposé avoir une valeur initiale φ = φ2 en a2 . Gouverné
par (5.57), le champ « descend » vers φ1 avec une vitesse qui approche la vitesse terminale φ̇ = −V /(3ȧ/a). Après a1 , le champ a des oscillations amorties autour de φ0 avant
de se stabiliser à son minimum. Pendant les oscillations une partie de l’énergie peut être
transformée en particules par des couplages appropriés.
ÉC
E
L
O
T
Y
L
PO
phénoménologiquement en ajoutant un terme Γφ̇ au membre de gauche de (5.57). Ici, Γ
est l’inverse du temps d’amortissement provenant du rayonnement de particules. Cela
mène à ce qu’une partie de l’énergie du champ est convertie en énergie de rayonnement.
Il faut souligner qu’alors que le potentiel de la ﬁgure 5.10 donne une densité
d’énergie semblable à celle de la ﬁgure 5.8, on peut résoudre les problèmes de l’horizon
et de Ω avec n’importe quel potentiel lentement variable. Un potentiel souvent évoqué
à cause de sa simplicité est
V (φ) = γ φ4 ,
(5.60)
où γ est une constante sans dimension3 . L’équation de Friedmann en unités naturelles
est alors
H2 =
8πγφ4
.
3mpl 2
Y
L
PO
H
C
TE
U
Q
I
N
(5.61)
Pour résoudre les problèmes de Ω et de l’horizon, on a besoin que l’inﬂation dure
pendant N ∼ 60 temps de Hubble. Cela met une contrainte sur la valeur initiale de
E
L
O
3 φ a la dimension d’une énergie, comme on peut le voir sur la forme générale du tenseur énergieimpulsion pour un champ scalaire (4.70).
ÉC
E
214
E
U
IQ
Chapitre 5. Applications de l’équation de Friedmann
φ2 :
E
L
O
PO
LY T
t1
Hdt ∼
t2
N
H
EC
0
H(φ)dφ/φ̇ > 60 .
(5.62)
φ2
En utilisant la condition de descente lente (5.58) on trouve que le champ doit être
initialement déplacé de son minimum d’une valeur comparable à la masse de Planck :
√
(5.63)
φ2 > N mpl .
ÉC
Alors que le lecteur peut être ou ou non impressionné par cette condition, elle met
une contrainte importante pour les gens qui se préoccupent de ce qui se passait avant
l’inﬂation. Sur ce plan, on notera que dans une classe de modèles [125] connus sous le
nom d’« inﬂation chaotique », le champ prend des valeurs aléatoires dans l’espace.
Seules les régions qui ont une valeur de φ suﬃsamment loin du minimum subissent
l’inﬂation.
On peut obtenir une contrainte sur la constante de couplage γ en considérant les
ﬂuctuations quantiques du champ φ. On pense que ces ﬂuctuations sont les graines des
ﬂuctuations de densité qui sont à l’origine des structures de l’univers d’aujourd’hui.
Nous verrons au chapitre 7 qu’on observe que les ﬂuctuations de densité actuelles sur
une échelle de H0−1 sont de l’ordre de ∆ρ/ρ ∼ 2 × 10−5. De plus, ces ﬂuctuations sont
reliées, comme on le verra, à la pente du potentiel pendant l’inﬂation :
ò
ï
H3
∆ρ
.
(5.64)
∼ ρ H0−1
V (φ)
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
Pour le potentiel γφ4 et ∆ρ/ρ ∼ 10−5 cela donne
(∆ρ/ρ)2
∼ 10−15 .
(5.65)
N3
Ceci veut dire que le φ est très faiblement couplé à lui-même, une conclusion qui se
retrouve pour tous les potentiels inﬂationnaires qui ont des ﬂuctuations quantiques
d’une amplitude convenable pour engendrer les ﬂuctuations de densité observées.
Alors que la condition (5.65) peut certainement être choisie classiquement, il est
diﬃcile de réaliser un couplage aussi faible dans une théorie quantique car les corrections quantiques au potentiel provoquent en général des couplages comparables aux
autres couplages, par exemple α ∼ 10−2 . C’est là le problème de base du scénario
inﬂationnaire. Alors qu’on peut trouver un champ et un potentiel classiques pour résoudre les divers problèmes cosmologiques, il n’existe à l’heure actuelle aucune théorie
quantique bien fondée qui satisfasse toutes ces conditions.
γ ∼
6
H
C
E
T
Diﬀusion et absorption intergalactique
Y
OL
P
E
L
ÉCO
U
Q
I
N
Comme dernière application de l’équation de Friedmann, nous allons montrer dans
cette section comment calculer la probabilité d’absorption ou de diﬀusion des photons dans l’espace intergalactique. Les processus les plus importants sont la diﬀusion
E
Diﬀusion et absorption intergalactique
T
Y
L
PO
N
H
EC
E
U
IQ
215
Compton sur les électrons libres et l’absorption résonante sur les atomes. Nous allons
traiter ce second processus et montrer que si la plupart de la matière baryonique
était non-ionisée, l’absorption serait suﬃsante pour éliminer tous les photons ultraviolets des sources de grand redshift. Le fait que de tels photons soient observés dans
les spectres de quasars distants est une indication expérimentale que la majorité de
l’hydrogène intergalactique est maintenant ionisée. Cette conclusion importante a été
tirée par Gunn et Peterson [126]. On pense généralement que la matière a été « réionisée » par les photons ultraviolets produits par les premières étoiles ou quasars.
ÉC
E
L
O
Considérons un photon émis à t1 avec une énergie E1 . Nous allons considérer une
réaction qui diﬀuse ou absorbe les photons sur un certain type de particule avec une
section eﬃcace σ(E). La probabilité dP qu’un photon soit diﬀusé ou absorbé entre t
et t + dt est
dP = n(t) σ(E(t)) cdt ,
E
U
IQ
(5.66)
N
H
EC
où n(t) est la densité de particules diﬀusantes ou absorbantes. Pour simpliﬁer les
choses, nous supposons que le nombre de particules est indépendant du temps :
LY T
Å
O
P
E
L
ÉCO
n(t) = n0
a0
a(t)
ã3
.
(5.67)
De plus, l’énergie du photon dans le référentiel de la matière absorbante est E(t) =
E1 a1 /a(t) et nous obtenons
Å
dP = n0
a0
a(t)
ã3
σ (E = E1 a1 /a(t)) cdt .
(5.68)
La profondeur optique totale P peut être calculée en intégrant entre t1 et t0 . Comme
d’habitude, les choses sont plus simples si l’on fait le changement de variable t → a(t).
En utilisant l’équation de Friedmann, on trouve :
1
σ (E = E1 a1 /a) dâ
.
(5.69)
P = dH n0
1/2
4
−3
+ ΩΛ + (1 − ΩT )â−2 ]
â1 â [ΩM â
U
Q
I
N
Les photons de la transition n = 2 → n = 1 de l’hydrogène atomique, d’énergie
égale à E1−2 = (3/4)0.5α2 me c2 = 10.21 eV peuvent être absorbés par l’hydrogène
atomique dans son état fondamental, par excitation du niveau 2p, ce qu’on appelle la
transition Lyman-α. La section eﬃcace est
Y
L
PO
σT
σ(E) = f 3 E1−2 δ(E − E1−2 )
α
E
L
O
H
C
TE
f = 0.416 ,
(5.70)
où σT est la section eﬃcace Thomson et α ∼ 1/137. L’expansion de l’univers garantit
qu’un photon émis avec une énergie E1 > E1−2 sera ultérieurement déplacé vers le
rouge jusqu’à l’énergie de résonance.
ÉC
E
216
E
U
IQ
Chapitre 5. Applications de l’équation de Friedmann
T
Y
L
PO
N
H
EC
En insérant la section eﬃcace (5.70) dans (5.69) on trouve :
P =
ÉC
E
L
O
ñ
×
βf
(dH ne σT )
α3
ô
1
,
1/2
â3 [ΩM â−3 + ΩΛ + (1 − ΩT )â−2 ]
(5.71)
a=a1 E1 /E1−2
où ne ∼ nb est la densité d’électrons actuelle et β est la fraction d’électrons qui sont liés
dans l’état fondamental de l’hydrogène intergalactique. En appliquant cette formule
aux photons d’énergie E1 un tout petit peu plus grande que E1−2 et en utilisant la
valeur de nb donnée par la nucléosynthèse, on trouve
P =
(9.4 × 102 ) β (z + 1)3
1/2
[ ΩM (z + 1)3 + ΩΛ + (1 − ΩT )(z + 1)2 ]
N
H
EC
E
U
IQ
,
(5.72)
où z est le redshift de la source. Pour z > 1, le grand facteur numérique garantit que
l’absorption sera complète sauf si β 1.
La ﬁgure 6.7 montre le spectre d’un quasar de grand redshift. Le pic proéminent
à 580 nm est dû à l’émission de Lyman-α par le quasar. Les photons du côté bleu de
ce spectre peuvent être absorbés par l’absorption Lyman-α après avoir été redshiftés.
En supposant que l’émission juste au dessus de l’énergie de Lyman-α n’est pas très
diﬀérente de l’émission juste au dessous, on voit que l’absorption moyenne de photons
de haute énergie est de l’ordre de 0.5. Par conséquent, la plupart de l’hydrogène
intergalactique est ionisé :
ÉC
E
L
O
T
Y
L
PO
β ∼ 10−4 .
(5.73)
Cette limite suppose que la plupart de l’hydrogène est, en eﬀet, intergalactique, ce à
qui on s’attend d’après les simulations hydrodynamiques [31].
Exercices
5.1 Les intégrales (5.6) et (5.7) sont triviales pour les trois modèles cosmologiques
suivants :
ΩΛ = 0, ΩR ∼ 0
ΩM = 1
ΩM = ΩΛ ∼ 0
ÉC
ΩΛ = 1
E
L
O
critique, dominé par la matière
Y
L
PO
ΩR ∼ 0
ΩM ∼ ΩR ∼ 0
H
C
TE
U
Q
I
N
vide
critique, dominé par le vide
E
Exercices sur le chapitre 5
T
Y
L
PO
N
H
EC
E
U
IQ
217
Pour ces trois modèles :
(a) Calculer a(t) et q0 .
(b) Calculer l’âge de l’univers, en négligeant ΩR . Quel univers verrait son âge fortement modiﬁé par l’oncorporation du rayonnement ?
(c) Calculer dL (z) et dA (z) (en négligeant ΩR ) et dessiner leur dépendance en fonction
de log z entre z = 10−3 et z = 103 .
(d) Noter que pour le premier modèle, dA (z) → 0 pour z → ∞ (et pour z → 0).
Trouver le redshift pour lequel dA est maximisé et la taille angulaire d’un objet est
minimisée.
ÉC
E
L
O
5.2 Si tous les neutrinos ont des masses inférieures à ∼ 1 eV, l’équation de Friedmann
à teq prend la forme appropriée à trois espèces de neutrinos sans masse avec nν =
(3/11)nγ (par espèce) :
E
U
IQ
1/2
ȧ
= H0 1.668Ωγ â−4 + ΩM â−3 + ΩΛ + (1 − ΩT )â−2
.
a
N
H
EC
(5.74)
Pendant quelle durée temporelle cette approximation doit-elle être bonne pour
l’équation de Friedmann ? Calculer teq et trec en fonction de ΩM , ΩR et ΩΛ en considérant seulement des valeurs « réalistes » de ces paramètres. On justiﬁera toute
approximation que l’on sera amené à faire.
ÉC
E
L
O
T
Y
L
PO
5.3 Calculer l’âge d’un univers presque critique avec ΩΛ = 0 et ΩT = ΩM = 1 + ,
1. Vériﬁer que pour < 0 l’âge est compris entre celui d’un univers critique
dominé par la matière et celui d’un univers vide.
5.4 Calculer l’âge d’un univers critique ΩT = ΩM +ΩΛ = 1 dans la limite ΩΛ << ΩM .
Vériﬁer que pour ΩΛ > 0, l’âge est supérieur à l’âge d’un univers avec ΩΛ = 0.
5.5 Le nombre de galaxies dN de coordonnée radiale compise entre χ1 et χ1 + dχ,
dans l’angle solide dΩ, et au temps t1 est
dN = n1 a1 dχ a21 r12 dΩ ,
U
Q
I
N
(5.75)
où n1 est la densité de galaxies à t1 . Si l’on suppose que le nombre de galaxies est
conservé, n1 a31 = n0 a30 cette expression devient
Y
L
PO
dN = n0 a0 dχ a20 r12 dΩ .
Utiliser (5.19) pour montrer que
E
L
O
H
C
TE
dN
= n0 H0−3 z 2 [1 − 2(q0 + 1)z + .....] .
dzdΩ
ÉC
(5.76)
(5.77)
E
218
E
U
IQ
Chapitre 5. Applications de l’équation de Friedmann
T
Y
L
PO
N
H
EC
Cette relation montre comment la distribution du redshift des galaxies peut être
utilisée pour déterminer q0 . En pratique, cette relation est extrêmement diﬃcile à
utiliser car, comme nous l’avons souligné dans la section 2, le nombre de galaxies diverge logarithmiquement aux basses luminosités. Il est donc nécessaire de sélectionner
des galaxies de luminosité intrinsèque supérieure à une certaine valeur. Malheureusement, on sait que la luminosité intrinsèque d’une galaxie varie avec le temps et, par
conséquent, avec le redshift. Il est donc diﬃcile de séparer les eﬀets d’évolution de la
luminosité et l’eﬀet dû à q0 .
Au lieu de sélectionner les galaxies par leur luminosité, il peut être possible de
sélectionner les galaxies au dessus d’une certaine masse en mesurant les largeurs Doppler des raies spectrales galactiques [127]. Puisque l’évolution de masse est mieux
comprise que celle de la luminosité, cette technique peut permettre la mesure de q0
avec (5.77).
Il est aussi possible d’appliquer (5.77) aux amas de galaxies. On s’attend à ce que
le nombre d’amas de galaxies évolue de façon calculable. Comme nous le verrons dans
la section 2, cette technique est sutout sensible à ΩM plutôt qu’à q0 .
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
5.6 Montrer que la généralisation relativiste de la relation de Sunyaev-Zel’dovoch
(SZ) (2.30) est
ÉC
√
P 2 cα∆θ me T n2e a0 χ1 (z) ∼
.
4πφX σT (1 + z)3 ne 2
E
L
O
(5.78)
L’utilisation de (5.19) permet alors de déterminer q0 une fois mesurées les quantités
du membre de droite.
5.7 Généraliser la discussion de la méthode de la photosphère en expansion de la
section 5.1 pour montrer que
vt
a0 χ1 (z) =
(1 + z)2
Å
σT 4
φ
ã1/2
,
(5.79)
où v est la vitesse d’expansion de la photosphère, t le temps observé depuis l’explosion,
φ le ﬂux d’énergie observé, et T la température de surface. L’utilisation de (5.19)
permet alors de déterminer q0 .
H
C
TE
U
Q
I
N
5.8 Considérons un univers fermé avec ΩT = ΩM > 1.
(a) Calculer l’horizon actuel χhor = χ1 (z = ∞).
(b) Quelle fraction de l’univers est à l’heure actuelle en deçà de l’horizon (χ < χhor ) ?
Trouver une expression simple pour le cas (ΩT − 1) 1.
(c) Montrer qu’au moment d’expansion maximale l’horizon contient l’univers tout
entier : χhor (amax ) = π.
ÉC
E
L
O
Y
L
PO
E
Exercices sur le chapitre 5
T
Y
L
PO
N
H
EC
E
U
IQ
219
(d) Monter que l’âge de l’univers à l’expansion maximale est
t(amax ) = H0−1
E
L
O
πΩT
2(ΩT − 1)3/2
ΩM = ΩT > 1 .
(5.80)
(e) Montrer que l’âge d’un univers formé seulement de rayonnement est, au maximum
d’expansion,
ÉC
t(amax ) = H0−1
1
ΩT − 1
ΩR = ΩT > 1 .
(5.81)
5.9 Considérons un univers ouvert (ΩT ≤ 1). Montrer que si ΩΛ = 0 tout l’univers
se trouvera un jour dans notre horizon. Montrer que si ΩΛ > 0 l’horizon approchera
une limite ﬁnie. Ceci montre qu’un univers avec ΩΛ > 0 possède un « horizon des
événements » au delà duquel nous ne pourrons jamais faire d’observation.
T
Y
L
PO
N
H
EC
E
U
IQ
5.10 Considérons un univers ouvert (ΩT < 1) avec ΩΛ = 0. Montrer que
√
2 1 − ΩT
lim r(z) = sinh(χhor ) =
ΩΛ = 0 .
z→∞
ΩT
E
L
O
(5.82)
Montrer que la distance angulaire à grand redshift est
ÉC
lim dA (z) =
z→∞
2H0−1
zΩT
ΩΛ = 0 .
(5.83)
5.11 Calculer θH pour ΩT = 1 dans la limite ΩΛ ΩM . Expliquer pourquoi θH dans
la ﬁgure 5.5 est presque indépendant des valeurs relatives de ΩM et ΩΛ si ΩT = 1.
5.12 Au 18e siècle, Olbers et Chéseaux remarquèrent que si l’univers est homogène
dans l’espace et dans le temps, la lumière intégrée des étoiles est inﬁnie. Pour reconstruire leur argument, on considèrera un univers statique composé d’objets ﬁxes de
nombre volumique n0 et de luminosité par objet L indépendante du temps.
(a) Considérer les objets vus dans un angle solide dΩ de l’origine. Quel est le ﬂux
total de photons à l’origine venant de ces objets ? C’est là le paradoxe d’Olbers.
(b) Expliquer pourquoi l’absorption par de la matière interposée ne résoud pas le
paradoxe.
(c) En supposant que l’univers n’a existé que pendant un temps t0 , quel est le ﬂux
total ? Cela résout le paradoxe de façon adhoc.
Considérons maintenant le modèle cosmologique standard (du 21e siècle). Pour
simpliﬁer les choses, nous allons supposer que le nombre de galaxies est constant dans
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
220
E
U
IQ
Chapitre 5. Applications de l’équation de Friedmann
le temps :
E
L
O
T
Y
L
PO
N
H
EC
n(t) = n0
a 3
0
a
.
Nous supposons également que leur luminosité L est indépendante du temps.
(d) Quel est le nombre de galaxies dans l’angle solide dΩ avec une coordonnée radiale
entre χ1 et χ1 + dχ1 ? Quel est le ﬂux venant de ces objets ?
(e)
Quel est le ﬂux total d’objets dans l’angle solide dΩ. Exprimer le ﬂux comme
une intégrale sur le temps d’émission t1 . Exprimer le ﬂux comme une intégrale sur
le paramètre d’échelle a(t1 ). Évaluer l’intégrale dans les cas ΩM = ΩT = 1 et ΩM =
ΩT = 0. Comparer le ﬂux total résultant avec le ﬂux dans la partie c.
(f ) Dans une cosmologie inﬂationnaire avec seulement des photons, on peut considérer que les photons du CBR ont été produits à la ﬁn de l’époque inﬂationnaire
par la transformation d’énergie du vide en rayonnement. Pour calculer le ﬂux de ces
photons, on peut remplacer le facteur n(t)L par ρV δ(t − t1 ). Calculer le ﬂux résultant
et commenter le résultat.
(g) Calculer le ﬂux de photons que nous recevrons dans le futur lointain. Comparer
les résultats pour ΩM = ΩT = 1, ΩM = ΩT = 0 et le modèle préféré actuellement
ΩM = 0.3, ΩΛ = 0.7.
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
5.13 L’eﬀet Gunn-Peterson indique que la plupart des baryons intergalactiques sont
ionisés. Les photons peuvent donc subir une diﬀusion de Thomson sur les électrons
libres avec une section eﬃcace σT .
(a) Appliquer (5.69) à la diﬀusion Thomson avec n = ne ∼ nb .
(b) Évaluer les intégrales dans le cas (ΩM = 1, ΩΛ = 0). La diﬀusion Thomson
inhibe-t-elle de façon signiﬁcative l’observation d’objets de grand redshift ?
ÉC
5.14 (Suite de l’exercice 3.9) Un explorateur quitte notre galaxie à t0 avec une vitesse
v c après avoir utilisé tout son carburant. En utilisant l’équation du mouvement
trouvée dans la section 7, calculer le redshift de la galaxie la plus lointaine qui puisse
être visitée dans les cas (ΩT = ΩM = 1), (ΩT = ΩM = 0), et (ΩT = ΩΛ = 1).
U
Q
I
N
5.15 On peut supposer qu’à une époque future t, la technologie aura progressé au
point que nous pourrons quitter la galaxie avec une vitesse v ∼ c. Calculer le redshift
de la galaxie la plus lointaine qui pourra être visitée dans les cas (ΩT (t) = ΩM (t) = 1),
(ΩT (t) = ΩM (t) = 0), et (ΩT (t) = ΩΛ (t) = 1). Interpréter le résultat pour un univers
dominé par le vide.
ÉC
E
L
O
Y
L
PO
H
C
TE
E
T
Y
L
PO
N
H
EC
E
U
IQ
E
L
6
CO
ÉChapitre
L’histoire thermique de
l’univers
T
Y
L
PO
N
H
EC
E
U
IQ
Ces temps-ci, il ne se passe pas grand’chose dans l’espace intergalactique. Il ne se
produit pas de réactions nucléaires et les photons et neutrinos ne diﬀusent que très
rarement sur la matière. Plus quantitativement, le nombre de réactions par unité de
temps, Γ, est beaucoup plus faible qu’une réaction par temps de Hubble. Par exemple,
le taux de diﬀusion Compton par photon est
ÉC
E
L
O
Γγe→γe = ne σT c ∼ 1.4 × 10−3 H0 ,
(6.1)
ce qui signiﬁe que seul un photon sur 700 va subir une collision dans le prochain temps
de Hubble. Tant que l’univers va continuer à se dilater, les réactions vont devenir de
plus en plus rares au fur et à mesure que décroît la densité. De fait, nous verrons
qu’un photon typique ne sera jamais rediﬀusé.
Les choses étaient tout autres dans les premiers temps de l’univers. Juste avant
d’électrons était 109 fois la densité actuelle
la recombinaison, ârec ∼ 10−3 , la densité √
alors que le taux d’expansion n’était que ΩM 10003/2 ∼ 2 × 104 fois le taux actuel :
Γγe→γe (trec ) ∼ ne (trec ) σT c ∼ 80 H(trec ) .
(6.2)
U
Q
I
N
À cette époque, un photon typique subissait 80 collisions par temps de Hubble.
Nous verrons que le spectre thermique des photons provient du taux de réaction
élevé dans les premiers temps de l’univers. La diﬀusion élastique, par exemple
γe− ↔ γe− ,
Y
L
PO
H
C
TE
(6.3)
provoquait des échanges d’énergie entre particules et engendrait un équilibre « cinétique » , c’est-à-dire une distribution thermique d’impulsion. Les réactions inélastiques, comme
ÉC
E
L
O
e− p ↔ e− pγ ,
221
(6.4)
E
222
E
U
IQ
Chapitre 6. L’histoire thermique de l’univers
T
Y
L
PO
N
H
EC
changeaient le nombre de particules et engendraient un équilibre « chimique » où les
densités de particules ont des valeurs thermiques. Des exemples importants pour ce
chapitre sont les réactions élémentaires
ÉC
E
L
O
γγ ↔ e+ e− ↔ ν ν̄ .
(6.5)
Dans l’univers primordial, ces réactions engendraient des densités thermiques (de
corps noir) de paires électron–positron et de neutrinos. Les transitions neutron-proton
sont également importantes :
νe n ↔ e− p
ν̄e p ↔ e+ n .
(6.6)
Ces réactions ont provoqué l’équilibre chimique entre protons et neutrons, déterminant
ainsi le nombre de neutrons disponibles pour la nucleosynthèse.
Nous verrons que la condition minimale pour que s’établisse l’équilibre thermique
est que le taux de réaction par particule soit supérieur au taux d’expansion :
Γ ȧ
a
⇒
HN
équilibre thermique .
C
E
T
LY
E
U
IQ
(6.7)
La taux d’expansion est le paramètre important car son inverse, tH , donne le temps
caractéristique des changements de température et de densité dus à l’expansion universelle. Les collisions peuvent par conséquent faire les ajustements nécessaires des
distributions d’impulsion et des distributions chimiques seulement si chaque particule
subit une réaction au moins une fois par temps de Hubble.
À cause de l’expansion, l’époque de collision ne peut que se terminer lorsque le
taux de réaction devient plus faible que le taux d’expansion, Γ ȧ/a. Ce qui arrive
aux distributions thermiques une fois que les collisions cessent dépend du type d’équilibre. Pour un équilibre purement cinétique, c’est-à-dire le spectre en impulsion des
particules, le caractère thermique du spectre peut se maintenair pendant l’expansion.
C’est le cas des photons du CBR.
D’un autre côté, l’équilibre thermique chimique est maintenu seulement par les
réactions et l’équilibre cesse dès que cessent les réactions. C’est le cas pour les noyaux.
À la température actuelle, l’équilibre chimique impliquerait que les nucléons tendent
à se trouver dans leurs états les plus solidement liés, au voisinage du 56 Fe. Ce n’est
pas le cas, car les réactions nucléaires nécessaires pour atteindre cet état ont cessé
lorsque la température était bien supérieure. La plupart des nucléons étaient « en
place » dans l’hydrogène et dans l’hélium. On dit que les réactions nucléaires ont été
« gelées » à une température Tg qui se trouve être de l’ordre de Tg ∼ 30 keV. Le
« gel » a laissé l’univers avec un « reliquat » de densité de noyaux d’hydrogène et
d’hélium très loin de la densité à l’équilibre.
Le gel nucléaire a laissé l’univers avec une réserve d’énergie libre, c’est-à-dire
d’énergie qui peut maintenant être dégradée par des réactions nucléaires de fusion exothermiques et productrices d’entropie. En particulier, l’hydrogène peut être converti
en hélium, l’hélium peut être converti en éléments plus lourds une fois que la matière est conﬁnée gravitationnellement dans les étoiles. Les réactions de fusion dans
O
P
E
L
ÉCO
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
T
Y
L
PO
N
H
EC
E
U
IQ
223
les intérieurs stellaires transforment la masse en de l’énergie cinétique des produits
de réaction qui est ensuite dégradée en énergie thermique y compris une multitude
de photons thermiques. C’est cet accroissement du nombre des photons qui est principalement responsable de l’acccroissement d’entropie1.
Après que les photons se sont échappé d’une étoile, la production d’entropie peut
se poursuivre si ces photons sont interceptés par une surface planétaire froide. Sur
la Terre, chaque photon solaire est « démultiplié » en ∼ 20 photons thermiques
(T ∼ 300 Kelvin). L’accroissement correspondant d’entropie fait plus que compenser
la diminution d’entropie associée à l’organisation de la vie induite par la photosynthèse. Sans le grandient thermique entre le Soleil et la Terre, la photosynthèse ne
serait pas possible à cause du deuxième principe de la thermodynamique. On voit que
la cessation d’équilibre thermique nucléaire dans l’univers primordial fournit l’énergie libre nécessaire à la vie sur Terre. Sans cette source d’énergie, la vie dépendrait
des photons émis par eﬀondrement gravitationnel (exercice 2.10), source qui serait
épuisée plus rapidement.
L’explication du déséquilibre thermique actuel est un des grands triomphes de la
cosmologie moderne. Ce déséquilibre intriguait les physiciens du XIXe siècle car il
savaient que tout système isolé tend vers l’équilibre thermique. Ils se préoccupaient
également de la « mort thermique » future de l’univers lorsque serait atteint l’équilibre, ce qui mettrait ﬁn à toute activité intelligente. La cosmologie moderne a renversé
l’ordre des événements. L’état d’équilibre thermique a eu lieu dans le passé plutôt que
dans le futur. Nous verrons que les perspectives du futur ne sont pas particulièrement roses, mais qu’il nous reste encore quelque temps pour proﬁter de notre réserve
d’énergie libre.
La plupart de ce chapitre portera sur la transition entre les époques de collisions
vers les époques sans collisions et sur les reliquats de densité de diverses espèces. Les
calculs précis se font la plupart du temps avec des codes informatiques compliqués,
mais nous nous limiterons à des arguments qualitatifs aﬁn de comprendre la physique
sous-jacente.
Les deux premières sections introduisent les outils nécessaires. Dans la section 1
nous présentons les distributions de particules dans l’espace des phases qui décrivent
l’état thermique de l’univers. Dans la section 2 nous montrerons comment les distributions dans l’espace des phases sont régies par l’équation de Boltzmann couplée à
l’équation de Friedmann .
Les sections suivantes appliqueront ces concepts aux électrons et positrons, aux
neutrinos, aux noyaux et aux wimps. (La recombinaison atomique sera traitée dans
l’exercice 6.5.) Nous verrons que toutes ces espèces étaient à l’origine en équilibre
thermique, ce qui entraîne que, pour des températures beaucoup plus grandes que leur
masse, leur nombre volumique était comparable à celui des photons. Quand le taux
de réaction a baissé, chaque espèce a quitté l’équilibre thermique laissant place à un
reliquat de densité de particules que nous observons aujourd’hui. Nous verrons que la
cosmologie standard permet de calculer les reliquats de densité. En particulier, nous
ÉC
E
L
O
ÉC
1 L’entropie
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
est toujours au moins proportionnelle au nombre de particules. Voir la Table 1.
E
224
E
U
IQ
Chapitre 6. L’histoire thermique de l’univers
T
Y
L
PO
N
H
EC
calculerons le rapport neutrino-photon « exactement » , le rapport hélium-hydrogène
en fonction du rapport baryon/photon, et le rapport wimp-photon en fonction de la
section eﬃcace d’annihilation des wimps (inconnue).
Pour des températures bien supérieures au GeV, les baryons et antibaryons étaient
présents sous la forme de quarks et d’antiquarks en nombres comparables à celui des
photons. Le petit reliquat de densité de baryons est due au petit excès de baryons
par rapport aux antibaryons à cette époque. Les sources possibles de cette asymétrie
seront discutées dans la section 7.
Dans la section 8 nous discuterons la question de savoir jusqu’à quel point l’expansion est réversible et nous identiﬁerons les processus qui nous permettent d’identiﬁer
la ﬂèche thermodynamique du temps cosmologique. Enﬁn, dans la section 9 nous présentons une discussion générale de ce que pourrait être le futur thermique de l’univers.
ÉC
1
E
L
O
Distributions à l’équilibre
N
H
EC
E
U
IQ
Dans ce chapitre, nous étudions la distribution dans l’espace des phases de chaque
espèce de particule i = γ, e− ...... :
LY T
Fi (r, p, t) =
O
P
E
L
ÉCO
dNi
3
d r d3 p
.
(6.8)
Dans certains cas il est commode de renormaliser la distribution à la quantité sans
dimension :
fi (r, p, t) =
Fi
,
gi /(2π)3
(6.9)
où gi est le nombre d’états de spin de l’espèce. La normalisation de fi est telle que fi =
1 correspond à la densité maximum dans l’espace des phases permise par le principe
de Pauli pour un fermion, Fi = gi /(2π)3 . Comme d’habitude, nous n’écrirons plus
explicitement les facteurs , c ou k.
Nous ne nous intéresserons qu’aux eﬀets locaux si bien que r et t peuvent être
choisis comme étant ceux de notre système de coordonnées en chute libre. L’hypothèse
d’homogénéité nous assure que les conclusions auxquelles nous parviendrons pour les
conditions à l’origine s’appliqueront aux conditions vues par tous le observateurs
comobiles. Dans le reste de ce chapitre, nous supprimerons donc le r = 0 parmi les
arguments des fonctions de distributions.
Hormis les contraintes du principe de Pauli pour les fermions, les distributions
fi sont a priori arbitraires. Les distributions thermiques à l’équilibre sont, toutefois,
particulièrement importantes :
fi (
pi ) =
E
L
O
Y
L
PO
H
C
TE
1
,
exp [ (Ep − µi )/T ] ± 1
U
Q
I
N
(6.10)
où T et µi sont la température et le potentiel chimique et où le signe + (−) correspond
aux fermions (bosons). Dans les applications cosmologiques, le potentiel chimique est
ÉC
E
Distributions à l’équilibre
T
Y
L
PO
N
H
EC
E
U
IQ
225
Tab. 6.1: Fonctions thermodynamiques à l’équilibre (6.11), (6.12), (6.13), et (6.14) dans
deux cas limites. Le premier est la limite relativiste (m T ) avec des nombres égaux de particules et d’antiparticules, c’est-à-dire µ T . Le second est la limite diluée, non-relativiste
(m T ) et m − µ T , qui implique f 1.
ÉC
E
L
O
fonction
m T, µ T
m−µT
n(T, µ)
g(1.2/π 2 )T 3
(×3/4 fermions)
g (mT /2π)3/2 e(µ−m)/T
ρ(T, µ)
g(π 2 /30)T 4
(×7/8 fermions)
(m + 3T /2 ) n
p(T, µ)
ρ/3
s(T, µ)
g(2π 2 /45)T 3
Tn
E
L
O
T
Y
L
PO
(×7/8 fermions)
N
H
EC
E
U
IQ
(m + 5T /2 − µ)n/T
en général déterminé par le nombre de particules (si ce nombre est ﬁxe) ou par la
diﬀérence entre le nombre de particules et d’antiparticules (voir exercice 6.1).
Le nombre volumique ni , la densité d’énergie ρi , et la pression partielle pi sont
déterminés par fi
gi
d3 pfi (
ni =
p) ,
(6.11)
(2π)3
ÉC
gi
ρi =
(2π)3
pi =
gi
(2π)3
d3 p Ep fi (
p) ,
d3 p
|
p|2
fi (
p) .
3E
H
C
TE
(6.12)
U
Q
I
N
(6.13)
Les déﬁnitions de ρ et p sont cohérentes avec celles données au chapitre 4 dans le
contexte du tenseur d’énergie-impulsion.
À l’équilibre thermique, fi est donné par (6.10), et les trois quantités sont fonction
de T et µ. Dans les limites relativiste et non-relativiste, il est facile de faire les intégrations (exercice 6.1) où tout, sauf les facteurs numériques, est déterminé par analyse
dimensionnelle. Les résultats sont donnés dans la Table 1 dans les deux limites les
plus intéressantes en cosmologie. La première est la limite relativiste (T m) avec
(T µ). Nous ne considérons que le cas µ ∼ 0 car il correspond à un nombre de
ÉC
E
L
O
Y
L
PO
E
226
1 Tev
E
L
O
100
ÉC
E
U
IQ
Chapitre 6. L’histoire thermique de l’univers
g =
E
?
T
Y
L
PO
N
H
EC
1 GeV
ρ
100
quark−gluon transition
π2 Τ4
30
10.75
10
gS =
1 MeV
10
S
3.91
2 π 2 Τ3
45
E
U
IQ
3.36
1
1 Tev
1 GeV
T
Y
L
PO
N
H
EC
1 MeV
gS
gE
T
Fig. 6.1: Nombres eﬀectifs d’états de spin, gE et gs , à l’équilibre en fonction de la tempéra-
E
L
O
ture. Seules les particules connues ﬁgurent dans la Table 6.2. Pour T < 1 MeV, Tγ = Tν ce
qui implique gs = gE .
ÉC
particules presque égal au nombre d’antiparticules comme c’était le cas, par exemple
pour les électrons et positrons lorsque T me . Dans la Table 1 on remarque la présence des facteurs habituels T 4 et T 3 pour la densité d’énergie et le nombre volumique
de « corps noirs ». Les facteurs (7/8) et (3/4) proviennent du principe de Pauli pour
les fermions (signe + dans (6.10)). Les facteurs sont plus petits que 1 car le principe
de Pauli impose fi ≤ 1.
Le second cas dans la Table 1 est celui d’un gaz non-relativiste dilué : (m −
µ T ) ce qui implique f 1. Dans ce cas, le facteur de Boltzmann exp(−m/T )
diminue radicalement le nombre de particules. Pour µ = 0, il n’y a ni particules ni
antiparticules si la température s’annule, n(T = 0, µ = 0) = 0.
À l’équilibre thermique, la densité d’entropie s est donnée par (exercice 6.2) :
ρ + p − µn
.
s(T, µ) =
T
H
C
TE
U
Q
I
N
(6.14)
Comme on l’a vu dans la Table 1, la densité d’entropie est proportionnelle au nombre
de particules. Parce que leur nombre n’est pas limité par un facteur de Boltzmann,
les espèces relativistes dominent en général la densité d’entropie. Aujourd’hui, elle
est dominée par les photons et les neutrinos. Aux températures plus élevées, elle
était dominée par des particules en équilibre thermique avec m < T . En supposant
une température unique T et des potentiels chimiques nuls, la densité d’entropie est
ÉC
E
L
O
Y
L
PO
E
Distributions à l’équilibre
T
Y
L
PO
N
H
EC
E
U
IQ
227
Tab. 6.2: Espèces de particules connues que l’on s’attend à être en équilibre thermique dans
E
L
O
l’univers primordial [21]. La masse donne la température minimum pour laquelle l’espèce est
relativiste, sauf pour les quarks légers et les gluons dont on attend qu’ils n’existent en tant que
particules libres seulement au dessus de la température de transition de phase ∼ 400 MeV.
Au dessous de cette température, les quarks sont liés dans des hadrons, principalement des
mésons π avec un petit nombre de mésons K, de nucléons et d’autres hadrons excités. Le
nombre eﬀectif d’états de spin, g, est le produit de 3 facteurs. Le premier est le nombre de
sous-espèces y compris les antiparticules, par exemple 1 pour le photon et 6 pour les neutrinos
(6 = 3 neutrinos plus 3 antineutrinos). Le deuxième facteur est le nombre d’états de spin
qui interagissent par sous-espèce, 1 pour les neutrinos, 2 pour les autres fermions de spin
1/2, 2 pour les bosons de spin 1 et de masse nulle, et 3 pour les bosons massifs de spin 1.
Enﬁn, le facteur (7/8) provient du principe de Pauli pour les fermions.
ÉC
particule
masse
photon γ
0
neutrinos νe , νµ , ντ
< 10 eV
leptons chargés
e
µ
τ
N
H
EC
E
U
IQ
spin
g
1
1×2=2
0
1/2
6 × 1 × (7/8) = 5.25
0.511 MeV
105.66 MeV
1777.05 MeV
1
1
1
1/2
1/2
1/2
2 × 2 × (7/8) = 3.5
2 × 2 × (7/8) = 3.5
2 × 2 × (7/8) = 3.5
quarks (3 couleurs)
d
u
s
c
b
t
∼0
∼0
∼ 170 MeV
∼ 1.3 GeV
∼ 4.3 GeV
∼ 170 GeV
−1/3
2/3
−1/3
2/3
−1/3
2/3
1/2
1/2
1/2
1/2
1/2
1/2
6 × 2 × (7/8) = 10.5
6 × 2 × (7/8) = 10.5
6 × 2 × (7/8) = 10.5
6 × 2 × (7/8) = 10.5
6 × 2 × (7/8) = 10.5
6 × 2 × (7/8) = 10.5
gluons g
0
0
1
8 × 2 = 16
bosons faibles
W
Z
80.41 GeV
91.187 GeV
1
0
1
1
ÉC
E
L
O
ÉC
charge
LY T
0
PO
E
L
O
Y
L
PO
H
C
TE
2×3=6
1×3=3
U
Q
I
N
E
228
E
U
IQ
Chapitre 6. L’histoire thermique de l’univers
donnée par
T
Y
L
PO
N
H
EC
s(T ) = gs (T )
E
L
O
2π 2 3
T ,
45
(6.15)
où le nombre eﬀectif d’états de spin est donné par la somme suivante sur toutes les
particules relativistes :
gs (T ) ∼
gi θ(T − mi ) + (7/8)
gi θ(T − mi ) ,
(6.16)
ÉC
bosons
fermions
où θ est la fonction de Heaviside. La fonction gs (T ) est dessinée sur la ﬁgure 6.1 pour
les particules connues dont la liste est dans la table 6.2.
Nous verrons que l’approximation d’une température unique n’est pas bonne pour
T < 1 MeV lorsque les neutrinos ont une température plus faible que les photons
Tν = (4/11)1/3 Tγ . À basse température, le nombre eﬀectif d’états de spin pour les
photons et trois espèces de neutrinos accompagnés de leurs antineutrinos est par
conséquent
N
H
EC
gs (Tγ me ) = 2 + 6 × (7/8)(Tν /Tγ )3 = 3.91 .
T
Y
L
PO
E
U
IQ
(6.17)
Pour calculer gs il faut se souvenir que pour les neutrinos et antineutrinos, un seul
des deux états d’hélicité interagit et peut être en équilibre thermique. La présence
possible des états d’hélicité sans interaction est discutée dans l’exercice 6.8.
Pendant l’époque du rayonnement, la densité d’énergie est dominée par des espèces
relativistes. Pour T > 1 MeV, il y a une température unique et la densité d’énergie
est
ÉC
E
L
O
ρ(T ) = gE (T )
π2 4
T
30
gE (T ) = gs (T )
(T > me ) .
(6.18)
Pour T < me la diﬀérence de température entre les photons et les neutrinos modiﬁe
gE (T ) de telle façon que gE (T ) = gs (T ) :
gE (Tγ me ) = 2 + 6 × (7/8)(Tν /Tγ )4 = 3.36 .
(6.19)
L’importance de la densité d’entropie s(T, µ) vient de ce que si l’univers est en
équilibre thermique, l’expansion est en bonne approximation adiabatique. Pour voir
d’où cela vient, nous remarquons que dans la section 2 nous avons montré que la
conservation locale de l’énergie implique
d(ρa3 ) = −p da3 .
T
Y
POL
H
C
E
U
Q
I
N
(6.20)
Pour un volume comobile (la région χ < χ1 1), cette équation équivaut à dE =
−pdV où V et E sont le volume de la sphère et l’énergie qu’elle contient. L’entropie
S dans le volume comobile varie suivant la relation fondamentale
dE + pdV − i µi dNi
dS =
,
(6.21)
T
ÉC
E
L
O
E
L’équation de Boltzmann
T
Y
L
PO
N
H
EC
E
U
IQ
229
où Ni est le nombre de particules de l’espèce i dans ce volume. La relation équivaut à
d(ρa3 ) + p da3 − i µi d(ni a3 )
.
(6.22)
d(sa3 ) =
T
E
L
O
Les deux premiers termes s’annulent l’un l’autre, donnant
ÉC
µi dni a3
dsa3
= −
.
3
da
T da3
i
(6.23)
En supposant que les potentiels chimiques sont négligeables, c’est-à-dire que les asymétries particule-antiparticule sont négligeables, il s’ensuit que
s(T ) a3 = gs (T ) T 3 a3 = constante .
(6.24)
E
U
IQ
Pour le domaine de températures où gs (T ) est constant, (6.24) implique
T ∝
1
,
a
T
Y
L
L’équation de Boltzmann
O
P
E
L
ÉCO
N
H
EC
(6.25)
ce qui donne la même dépendance de T en fonction de a(t) qu’en l’absence de collisions.
2
En l’absence de collisions, les particules se propagent librement dans l’espace des
phase suivant l’équation de Liouville. Dans la section 2.4 nous avons montré que dans
un univers homogène, l’équation de Liouville pour une particule d’espèce i de masse
nulle est :
ȧ
∂Fi
p Fi
=
p · ∇
∂t
a
⇒
a
∂Fi
p Fi .
= p · ∇
∂a
(6.26)
De fait, on peut montrer que cette équation s’applique aussi aux particules massives
(exercice 6.3) La solution générale est
F (
p, a) = F (
pa/a0 , a0 ) ,
(6.27)
ce qui signiﬁe que les distributions en impulsion sont déplacées vers le rouge pendant
l’expansion par un facteur a0 /a.
L’évolution du nombre volumique ni en l’absence de collisions se trouve en intégrant (6.26) sur l’impulsion :
ȧ
dni (t)
= −3 ni
dt
a
avec comme solution
ÉC
E
L
O
Y
L
PO
ni = ni (a0 )
H
C
TE
dni a3
= 0,
dt
⇒
a 3
0
a
.
U
Q
I
N
(6.28)
(6.29)
E
230
E
U
IQ
Chapitre 6. L’histoire thermique de l’univers
N
H
EC
Comme on s’y attend, le nombre volumique de particules décroît comme 1/a3 .
En présence de collisions, les particules se déplacent dans l’espace des phases non
seulement continûment par propagation libre, mais aussi de façon discontinue par
collisions discrètes. Nous voulons obtenir les généralisations de (6.26) et de (6.28) qui
tiennent compte des réactions élastiques et inélastiques. Pour simpliﬁer, considérons
seulement des réactions du type
ÉC
E
L
O
T
Y
L
PO
i + j ↔ k + l,
(6.30)
où i, j, k et l désignent des espèces de particules. Nous commençons avec la généralisation de (6.28) en écrivant symboliquement
ȧ
dni
= −3 ni − c(ij → kl) + c(kl → ij) ,
dt
a
(6.31)
E
U
IQ
où les deux termes que nous avons ajoutés tiennent compte de la perte et du gain des
particules i dans les réactions. On s’attend à ce que ces termes soient proportionnels
aux densités des particules dans l’état initial :
c(kl → ij) ≡ nk nl γkl→ij
N
H
EC
c(ij → kl) ≡ ni nj γij→kl .
T
Y
L
PO
(6.32)
Les constantes de proportionnalité, γ, ont la dimension d’un volume divisé par un
temps et sont en général interprétés comme des « sections eﬃcaces moyennes multipliées par la vitesse relative » (ou encore des taux de réaction par paires) :
ÉC
E
L
O
γkl→ij = σkl→ij vkl γij→kl = σij→kl vij .
(6.33)
C’est une interprétation intuitivement séduisante puisque l’on s’attend à ce que le
taux de réaction soit proportionnel à la section eﬃcace et à la vitesse relative. (Si
les particules sont au repos, elles ne peuvent entrer en collision.) L’interprétation est
particulièrement claire pour des collisions frontales si l’on fait abstraction des eﬀets
de particules identiques (principe de Pauli et émission stimulée)2 .
Il est utile de déﬁnir le taux de réaction par particule i
Γij→kl ≡ nj σij→kl v .
(6.34)
Nous remarquons que Γij→kl = Γji→kl . C’est simplement dû à ce que le taux de
réaction par particule i est proportionnel au nombre de particules j et vice versa.
L’équation (6.31) devient
ȧ
dni
= −3 ni + nk Γkl→ij − ni Γij→kl
dt
a
= −3
Y
L
PO
H
C
TE
ȧ
ni + nk nl σkl→ij v − ni nj σij→kl v .
a
E
L
O
U
Q
I
N
(6.35)
(6.36)
2 Les calculs quantiques donnent directement γ. Les sections eﬃcaces s’obtiennent en divisant γ
par le volume de normalisation et par la vitesse relative.
ÉC
E
L’équation de Boltzmann
T
Y
L
PO
N
H
EC
E
U
IQ
231
Les trois termes de cette équation décrivent les trois eﬀets qui changent ni : l’expansion de l’univers, la création des particules i, et la destruction des particules i.
Par exemple, si nous ne tenons pas compte des deux premiers termes dans (6.35), la
solution est ni ∝ exp(−t/τi ) où τi = 1/Γ(ij → kl) est la vie moyenne des particules i
par (ij → kl).
Dans l’introduction de ce chapitre, nous avons aﬃrmé que l’équilibre s’obtient si
les taux de réaction sont plus élevés que les taux d’expansion. La présence de ces
taux dans (6.35) nous donne une indication préliminaire de la façon dont ce résultat
apparaîtra. Si le taux d’expansion est beaucoup plus grand que le taux de réactions,
le premier terme domine. Dans le cas inverse, le terme de collision conduit le système
à l’équilibre thermique, comme nous le découvrirons bientôt.
Le terme d’expansion peut être combiné avec les termes de diﬀusion dans (6.35)
en calculant d(na3 )/dt puis d(na3 )/da3 :
Å ã−1
dni a3
ȧ
=
1/3
( nk Γkl→ij − ni Γij→kl )
(6.37)
3
da
a
ÉC
E
L
O
= 1/3
N
H
EC
Å ã−1
ȧ
( nk nl σkl→ij v − ni nj σij→kl v ) .
a
T
Y
L
PO
E
U
IQ
(6.38)
L’équation (6.38) est la généralisation voulue de (6.28). Nous l’utiliserons dans la
section suivante pour étudier l’évolution des densités de paires électron–positron, de
neutrinos, de noyaux et de wimps.
Avant de conclure cette section, il est utile de trouver la généralisation de l’équation de Liouville (6.26). Comme avec la généralisation de (6.28), on écrit formellement
ÉC
E
L
O
ȧ
pi , t)
∂Fi (
p Fi (
=
pi · ∇
pi , t) − C(ij → kl) + C(kl → ij) .
∂t
a
(6.39)
Le terme de collision C(ij → kl) s’obtient en sommant sur toutes les façons de perdre
une particule i d’impulsion pi :
dσij
pi ) d3 pj Fj (
pj )
gk d3 pk gl d3 pl 3
vij
C(ij → kl) = Fi (
d pk d3 pl
×(1 ∓ fk (
pk ))(1 ∓ fl (
pl )) .
U
Q
I
N
(6.40)
Les intégrales sur les impulsions de particule de type j, k et l, et les facteurs gj , gk
et gl , font la somme voulue. Les facteurs Fi (
pi ) et Fj (
pj ) reﬂètent que le taux de
ij → kl est proportionnel au nombre de particules i et j présentes initiallement. Les
facteurs (1 ∓ f (
p)) font respecter le principe de Pauli (signe − pour les fermions) ou
permettent l’émission stimulée (signe + pour les bosons).
Le terme de collision C(kl → ij) est évidemment
dσ(kl → ij)
pk )d3 pk Fl (
pl )d3 pl 3 3
vkl gj d3 pj
C(kl → ij) =
Fk (
d pi d pj
ÉC
E
L
O
Y
L
PO
H
C
TE
E
232
E
U
IQ
Chapitre 6. L’histoire thermique de l’univers
N
H
EC
×(1 ∓ fi (
pi ))(1 ∓ fj (
pj )) .
T
Y
L
PO
(6.41)
L’équation de Boltzmann se simpliﬁe si l’on tient compte du fait qu’en bonne
approximation les interactions des particules respectent l’invariance par renversement
du sens du temps. On s’attend donc à ce que le ﬁlm d’un processus individuel de
collision ait l’air aussi physique que le ﬁlm projeté en sens inverse. Cela implique que
le produit de la section eﬃcace par la vitesse d’une réaction directe soit égal au même
produit pour la réaction inverse :
ÉC
E
L
O
vij
dσ(ij → kl)
dγ(kl → ij)
= vjk
.
d3 pk d3 pl
d3 pi d3 pj
(6.42)
Dans cette approximation, nous pouvons combiner les deux termes de collision pour
trouver
∂Fi (
ȧ
pi , t)
p Fi (
=
pi · ∇
pi , t)
∂t
a
+
1
(2π)3
LY T
N
H
EC
gj d3 pj gk d3 pk gl d3 pl vij
O
P
E
L
ÉCO
E
U
IQ
dσ(ij → kl)
d3 pk d3 pl
× [fk fl (1 ∓ fi )(1 ∓ fj ) − fi fj (1 ∓ fk )(1 ∓ fl )] .
(6.43)
Dans le cas général, il y a une équation de Boltzmann pour chaque espèce i, chaque
équation contenant un terme de collision pour chaque type de réaction ijk.... →
λµν..... L’équation de Boltzmann couplée à l’équation de Friedmann forme un ensemble d’équations intégro-diﬀérentielles qui déterminent l’évolution de l’univers.
Étant donné la complexité de l’équation de Boltzmann, il n’est pas surprenant
qu’il n’existe pas de solution explicite et que les équations doivent être intégrées
numériquement aﬁn de trouver des solutions approximatives. Cette procédure ne pose
pas de problème car toutes les équations se ramènent, au bout du compte, à un système
d’équations diﬀérentielles couplées du premier ordre.
Deux cas limites ont des solutions approximatives intéressantes qui aident à comprendre les solutions numériques. Le premier est celui de l’absence de collisions (Γ H) dans quel cas la solution de l’équation de Boltzmann est donnée par (6.27) et
(6.29).
La seconde est celle d’un grand nombre de collisions pendant un temps de Hubble.
On s’attend alors à pouvoir, en première approximation, négliger le terme ȧ/a dans
(6.43). Dans ce cas, une solution dépendant du temps (∂f /∂t = 0) est telle que, pour
chaque combinaison d’impulsions pi , pj , pk , pl qui conserve l’impulsion et l’énergie,
la distribution satisfait
ÉC
E
L
O
Y
L
PO
H
C
TE
fk fl (1 ∓ fi ) (1 ∓ fj ) = fi fj (1 ∓ fk ) (1 ∓ fl ) ,
U
Q
I
N
E
L’équation de Boltzmann
c’est-à-dire
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
fi
fk
fl
fj
=
.
1 ∓ fk 1 ∓ fl
1 ∓ fi 1 ∓ fj
233
(6.44)
Cette condition est satisfaite si pour chaque espèce on a :
ÉC
fi
= exp [ (Ep − µi )/T ] ,
1 ∓ fi
(6.45)
µi + µj = µk + µl .
(6.46)
avec
L’équation (6.45) donne la distribution à l’équilibre thermique de Fermi–Dirac ou de
Bose–Einstein
fi (
pi ) =
1
,
exp [ (Ep − µi )/T ] ± 1
T
Y
L
PO
N
H
EC
E
U
IQ
(6.47)
où le signe + (−) correspond aux fermions (bosons). T est évidemment la température
et les µi sont les potentiels chimiques pour chaque espèce. La condition (6.46) peut être
généralisée de façon évidente à des réactions faisant intervenir plus de deux particules.
Notons que le terme de collision dans l’équation de Boltzmann (6.43) pousse les
distributions vers leur valeur à l’équilibre. Cela se produit eﬀectivement car si les fi
sont supérieurs (inférieurs) à leur valeur à l’équilibre, le terme de collision est négatif
(positif).
L’eﬀet de la contrainte chimique (6.46) dépend du type de réaction. La diﬀusion
élastique ne met évidemment aucune contrainte sur les potentiels chimiques. Les réactions inélastiques donnent des contraintes non-triviales. Par exemple, la réaction de
bremsstrahlung e− p ↔ e− pγ impose que le potentiel chimique des photons s’annule :
ÉC
E
L
O
µγ = 0 .
(6.48)
Cela veut dire que la distribution de photons à l’équilibre est la distribution de Planck.
De la même façon, le potentiel chimique de n’importe quelle espèce dont la production
n’est pas contrainte par la conservation d’un nombre quantique s’annule à l’équilibre
thermique.
La réaction e+ e− → γγ impose qu’à l’équilibre thermique
µe− = −µe+ .
T
Y
POL
H
C
E
U
Q
I
N
(6.49)
C’est également vrai de toute particule x en équilibre avec son antiparticule x̄ :
µx = −µx̄ .
E
L
O
(6.50)
Les distributions de Bose–Einstein et de Fermi–Dirac distributions ne sont pas des
solutions exactes de l’équation de Boltzmann (6.43) car elles ne tiennent pas compte
ÉC
E
234
E
U
IQ
Chapitre 6. L’histoire thermique de l’univers
T
Y
L
PO
N
H
EC
du terme proportionnel à ȧ/a. Ce terme rend, pour le moins, la température dépendante du temps. Si toutes les espèces sont approximativement en équilibre thermique,
cet eﬀet peut être inclus en utilisant tout simplement la conservation de l’entropie
pour une expansion adiabatique (6.24) dans le calcul la dépendance en temps de la
température.
Que les termes de collision dans l’équation de Boltzmann soient ou non suﬃsamment forts pour conduire un système à l’équilibre thermique dépend du type d’équilibre considéré. Nous verrons dans la section suivante que pour l’équilibre chimique, il
est suﬃsant en général d’avoir un taux de réactions qui changent les espèces plus grand
que le taux d’expansion. D’un autre côté, la façon d’approcher l’équilibre cinétique dépend de l’eﬃcacité d’échange d’énergie dans les collisions élastiques. Considérons par
exemple les photons produits par annihilation électron–positron lorsque la température est bien inférieure à la masse de l’électron. Ces photons ont des énergies bien plus
élevées que les photons thermiques. Pour se thermaliser, ces photons doivent perdre
de l’énergie par diﬀusion Compton. Le temps nécessaire pour cette thermalisation est
le sujet de l’exercice 6.6.
Dans la plupart des applications en cosmologie de l’univers primordial, le taux de
diﬀusion élastique est suﬃsant pour imposer l’équilibre cinétique. Les applications les
plus intéressantes sont celles de l’équilibre chimique entre espèces. Pour traiter ces
problèmes, il est nécessaire d’intégrer numériquement l’équation de Boltzmann (6.38)
en même temps que l’équation de Friedmann pour l’univers primordial
Å
ã
8πGρ 1/2
ȧ
=
,
(6.51)
a
3
ÉC
E
L
O
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
et l’équation de conservation de l’énergie
dρa3
= −p ,
da3
(6.52)
où p est la pression. À l’équilibre thermique cinétique, les membres de droite de ces
équations sont tous fonction de T et des µi . Elles peuvent être intégrées numériquement avec des conditions initiales sur ρ , p et les µi ou, de façon équivalente, pour
ρ, p et les ni . À chaque pas de l’intégration, ρ et les ni sont changés suivant la valeur de leur dérivée ce qui permet de calculer les nouvelles valeurs de T , p et des µi .
Manifestement, dans cette procédure, on est obligé de supposer que les distributions
d’impulsions sont thermiques.
Heureusement, des arguments qualitatifs permettent d’estimer plus facilement les
résultats d’une intégration numérique. Nous verrons comment cela se fait dans les
sections suivantes.
3
Y
L
PO
Électrons et positrons
E
L
O
H
C
TE
U
Q
I
N
Comme première application de l’équation de Boltzmann, nous allons traiter le
cas des électrons et positrons. Ces particules sont créées et détruites principalment
ÉC
E
Électrons et positrons
N
H
EC
E
U
IQ
235
dans la réaction e+ e− → γγ. Les deux équations de Boltzmann (6.38) sont
ÉC
E
L
O
T
Y
L
PO
dne− a3
dne+ a3
=
= 1/3
da3
da3
Å ã−1
ȧ
a
× nγ nγ σγγ→e+ e− v − ne− ne+ σe+ e− →γγ v .
(6.53)
On peut éliminer la section eﬃcace de σγγ→e+ e− dans (6.53) en utilisant le fait
qu’à l’équilibre thermique les distributions sont telles que le taux par unité de volume
de e+ e− → γγ est égal au taux de γγ → e+ e− :
nγ (T )2 σγγ→e+ e− vT = ne− (T ) ne+ (T ) σe+ e− →γγ vT ,
(6.54)
E
U
IQ
où les T signiﬁent que les densités et sections eﬃcaces moyennes doivent être évaluées
dans les conditions de l’équilibre thermique à la température T . L’équation (6.54) est
appelée « principe du bilan détaillé ». En supposant que la distribution en impulsion
des particules est telle que l’on peut approximer les sections eﬃcaces moyennes par
leur moyenne à l’équilibre thermique, σv ∼ σvT , (6.53) devient
LY T
N
H
EC
d(ne− a3 )
d(ne+ a3 )
=
= 1/3
da3
da3
O
P
E
L
ÉCO
Å ã−1
ȧ
a
× (ne− (T )ne+ (T ) − ne− ne+ ) σe− e+ →γγ v .
(6.55)
Le cas d’un univers symétrique , ne− = ne+ = ne est particulièrement simple :
d(ne a3 )
ne (T )2 − n2e Γe+ e− →γγ
.
= 1/3
3
da
ne
ȧ/a
(6.56)
Cette équation montre très clairement la physique de l’équation de Boltzmann. Si le
taux d’expansion est beaucoup grand que le taux d’annihilation, le membre de gauche
s’annule et la densité décroît comme a−3 . Si le taux de réaction n’est pas négligeable,
alors si ne est supérieur (inférieur) à la valeur à l’équilibre ne (T ), la dérivée de ne a3
est négative (positive). Il s’ensuit que la valeur de ne est poussée vers la valeur à
l’équilibre tant que le facteur de proportionnalité Γ/(ȧ/a) n’est pas trop petit. Il y a
donc deux limites et deux solutions simples. La première limite Γ ȧ/a correspond
à peu de réactions par temps de Hubble dans quel cas on a d(na3 )/dt ∼ 0 et
n ∝ a−3
H
C
TE
( Γ ȧ/a ) .
Y
L
PO
U
Q
I
N
(6.57)
La seconde limite est Γ ȧ/a qui correspond à de nombreuses réactions par temps
de Hubble. Dans ce cas, les abondances sont poussées vers leur valeur à l’équilibre :
ÉC
E
L
O
n = n(T )
( Γ ȧ/a ) .
(6.58)
E
236
ÉC
E
U
IQ
Chapitre 6. L’histoire thermique de l’univers
T
Y
L
PO
E
L
O
E
L
O
H
log H
ÉC
100
α2 T
Γ
log Γ(T)
N
H
EC
T
Y
L
PO
N
H
EC
Γ
E
U
IQ
e−m e /T
T 2 /m pl
10
1
−1
−2
10
10
Tf
T / me
Fig. 6.2: Taux d’annihilation Γ(e+ e− → γγ) et taux d’expansion H = ȧ/a en fonction de
la température dans les conditions de l’équilibre thermique et avec ne− = ne+ = ne . Pour
T > Tg , appelé Tf pour "freeze" dans la ﬁgure Γ > ȧ/a et ne prendra sa valeur à l’équilibre.
Pour T < Tg , Γ < ȧ/a et les réactions sont gelées. Après le gel, le nombre d’électrons et de
positrons est constant et ne décroît en 1/a3 .
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Électrons et positrons
T
Y
L
PO
N
H
EC
E
U
IQ
237
Pour déterminer si les électrons et les positrons sont en équilibre chimique avec les
photons, il suﬃt de calculer la valeur du taux d’annihilation à l’équilibre thermique
et de la comparer avec le taux d’expansion donné par l’équation de Friedmann :
ï
ò1/2
ï
ò
»
8πG
π2
T2
8πGρ 1/2
ȧ
=
∼
3gE (T )
(6.59)
=
gE (T ) T 4
a
3
3
30
mpl
où mpl = c/G = 1, 221 1019 GeV est la masse de Planck. (Comme nous ne nous
intéressons qu’aux résultats qualitatifs, on est tenté d’ignorer les facteurs numériques
ce que nous ferons parfois dans ce chapitre.)
Les taux d’expansion et d’annihilation sont montrés sur la ﬁgure 6.2. Pour le taux
d’annihilation, il y a deux limites simples, T me et T me . À haute température,
nous nous intéressons à de hautes énergies dans le centre de masse, Ecm me , où la
section eﬃcace d’annihilation est [128]
ÉC
E
L
O
2πα2
[ 2 ln(Ecm /me ) − 1 ]
2
Ecm
σe+ e− →γγ =
E
U
IQ
Ecm me .
N
H
EC
(6.60)
À basse énergie, v c, la section eﬃcace est proportionnelle à 1/v comme c’est
souvent le cas pour des réactions exothermiques :
T
Y
L
PO
vσe+ e− →γγ
E
L
O
πα2
=
m2e
v c.
(6.61)
Pour T me , les facteurs d’énergie dans la section eﬃcace se transforment en facteurs de température dans la section eﬃcace moyenne et (6.60) donne σv ∝ T −2
(en ignorant le facteur logarithmique). Les densités d’électrons et de positrons sont
proportionnelles à T 3 et le taux d’annihilation est donc proportionnel à la température :
ÉC
Γe+ e− →γγ ∼ α2 T
T me .
(6.62)
En comparant (6.59) et (6.62), on voit que Γ > ȧ/a pour T < α2 mpl ∼ 1014 GeV. Par
exemple, à T ∼ me , Γ ∼ (α2 mpl /me )ȧ/a ∼ 1018 ȧ/a, c’est-à-dire 1018 réactions par
temps de Hubble. Nous pouvons conclure que les électrons et les positrons étaient en
équilibre chimique avec les photons pour me < T < 1014 GeV.
On perd inévitablement l’équilibre pour T me car à l’équilibre le nombre d’électrons et de positrons tombe exponentiellement avec la température à cause du facteur
de Boltzmann e−m/T (Table 1). Dans le cas ne− = ne+ = ne , le taux d’annihilation à
l’équilibre est :
Y
L
PO
Γe+ e− →γγ
E
L
O
Å
∼ α
2
ÉC
T3
8πme
ã1/2
πα2
= ne (T ) 2
me
e−me /T
H
C
TE
(T me , ne− = ne+ ) .
U
Q
I
N
(6.63)
E
238
ÉC
E
U
IQ
Chapitre 6. L’histoire thermique de l’univers
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
T
Y
L
PO
N
H
EC
E
U
IQ
Fig. 6.3: log(ne /nγ ) en fonction de la température dans le cas ne = ne− = ne+ obtenu
numériquement en intégrant l’équation de Boltzmann . La ligne pointillée montre log(ne /nγ )
dans le cas de l’équilibre thermique.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Électrons et positrons
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
T
Y
L
PO
E
U
IQ
N
H
EC
239
E
U
IQ
Fig. 6.4: log(ne− /nγ ) en fonction de la température dans le cas (ne− − ne+ )/nγ = 3 × 10−10
U
Q
I
N
obtenu numériquement en intégrant l’équation de Boltzmann . La ligne pointillée montre
log(ne+ /nγ ).
ÉC
E
L
O
Y
L
PO
H
C
TE
E
240
E
U
IQ
Chapitre 6. L’histoire thermique de l’univers
T
Y
L
PO
N
H
EC
La ﬁn de l’équilibre chimique se produit en gros lorsque le taux d’annihilation (6.63)
est égal au taux d’expansion (6.59). La température à laquelle cela se produit est
appelée température de « gel » Tg parce qu’après que cette température est atteinte,
le nombre volumique comobile d’électrons et de positrons est gelé. En égalant les deux
taux, on obtient :
ÉC
E
L
O
Ç
»
Tg2
πα2
3gE (Tg )
= ne (T ) 2 = α2
mpl
me
Tg3
8πme
å1/2
e−me /Tg .
(6.64)
La solution numérique est
Tg ∼ me /40 .
(6.65)
E
U
IQ
Pour T < Tg , le taux d’annihilation est plus faible que le taux d’expansion et
l’équation de Boltzmann est simplement d(na3 )/da3 ∼ 0, qui implique
ne (a) ∼ ne (Tg )
a 3
g
a
T
Y
L
PO
N
H
EC
a > ag .
(6.66)
Pour a > ag le nombre volumique de photons est aussi proportionnel à a−3 et le
rapport entre le nombre d’électrons ou de positrons et le nombre de photons est
constant dans le temps. On peut estimer ce rapport en utilisant (6.65) :
ÉC
E
L
O
»
ne (ag )
ne (ag )
m2e
ne (a0 )
∼
∼
∼
g
(T
)
E
g
nγ (a0 )
nγ (ag )
Tg3
πα2 mpl Tg
∼ 2 × 10−16 .
(6.67)
Ce nombre est inférieur d’environ six ordres de grandeur au rapport observé pour les
électrons ne− ∼ ηnγ ∼ 5 × 10−10 nγ . Cela provient, bien entendu, de notre hypothèse
d’égalité entre le nombre d’électrons et de positrons.
La ﬁgure 6.3 montre le rapport entre le nombre d’électrons et le nombre de photons en fonction de la température, calculé numériquement en intégrant l’équation de
Boltzmann, l’équation de Friedmann (6.51), et l’équation de conservation de l’énergie
(6.52). On voit que l’estimation (6.67) est relativement précise. Il faut cependant insister sur le fait que nous n’avons pas pris grand soin des facteurs numériques, alors que
ces derniers ne peuvent être obtenus avec précision qu’en intégrant numériquement
l’équation de Boltzmann.
L’évolution de ne− et de ne+ dans un univers comme le nôtre avec un excès d’électrons est montrée sur la ﬁgure 6.4. Le reliquat de densité d’électrons est simplement
déterminée par conservation de la charge :
ÉC
E
L
O
Y
L
PO
H
C
TE
a30 ne− (t0 ) = a3 (ne− − ne+ ) .
U
Q
I
N
(6.68)
E
Neutrinos
T
Y
L
PO
N
H
EC
E
U
IQ
241
Nous pouvons relier cela à la densité de photons en utilisant le fait que tant que
l’équilibre thermique se maintient, l’entropie du système électron–positron-photon
est conservée :
E
L
O
sγe+ e− a3 = (2π 2 /45)gγe+e− (Tγ ) Tγ3 a3 = constante ,
ÉC
(6.69)
où gγe+e− (Tγ ) est le nombre eﬀectif d’états de spin pour le système γe+ e− à la température Tγ . Puisque l’équilibre est maintenu jusqu’à ce qu’il reste très peu d’électrons,
l’entropie du système électron–positron-photon pour T me est presque égale à
l’entropie du système de photons pour T me .
nγ a3 a0 = (1 + 2(7/8))nγ a3 T me ,
(6.70)
où nous avons fait usage de ce que sγ ∝ T 3 ∝ nγ . En divisant (6.68) par (6.70), on
trouve
ò
ò
ï
ï
ne− − ne+
ne−
= (11/4)
.
(6.71)
nγ a0
nγ
T >me
T
Y
L
PO
N
H
EC
E
U
IQ
Quant aux positrons, ils continuent de s’annihiler avec le nombre ﬁxe d’électrons
restants, en laissant un reliquat de densité de positrons qui est exponentiellement
négligeable (exercice 6.7).
4
ÉC
E
L
O
Neutrinos
Les trois espèces de neutrinos peuvent être produites ou détruites à T ∼ MeV par
la réaction
ν ν̄ ↔ e+ e− .
(6.72)
Comme cette réaction est une interaction faible (voir Appendice C), la section eﬃcace
pour toutes les espèces est de l’ordre de
σ ∼ G2F Eν2
me Eν mW ,
σ ∼ α2 Eν−2
Eν mW
Le taux d’annihilation est donc
Y
L
PO
Γν ν̄→e+ e− = nν σv ∼ G2F T 5
E
L
O
(6.73)
.
H
C
TE
me T m W .
U
Q
I
N
(6.74)
(6.75)
Numériquement, on trouve que le taux d’annihilation est supérieure au taux d’expansion H ∼ T 2 /mpl pour T > 1 MeV, et nous pouvons en conclure que pour des
températures supérieures à 1 MeV, les neutrinos étaient en équilibre chimique. Après
ÉC
E
242
E
U
IQ
Chapitre 6. L’histoire thermique de l’univers
N
H
EC
le gel des réactions d’annihilation à Tg ∼ 1 MeV, les neutrinos se découplent et leur
équation de Boltzmann devient
ÉC
E
L
O
T
Y
L
PO
dnν a3
∼ 0
da3
T < 1 MeV .
(6.76)
Nous sommes maintenant en mesure de comprendre pourquoi la température des
neutrinos de masse nulle est aujourd’hui inférieure à celle des photons. Pour T > me ,
les photons, neutrinos, et les électron–positrons étaient en équilibre thermique avec
une température unique, Te = Tγ = Tν . Mis à part les facteurs dus au Principe de
Pauli et la petite asymétrie électron–positron 3 , les nombres d’électrons, de positrons,
de neutrinos et de photons étaient les mêmes. Lorsque Te et Tγ sont tombés au dessous
de me les paires e+ e− ont été transformées en photons (par e+ e− → γγ) mais pas
en neutrinos découplés. Après ces annihilations, le nombre de photons était donc
supérieur au nombre de neutrinos. Puisque les distributions sont thermiques avec
n ∝ T 3 , il s’ensuit que Tγ > Tν pour T < me .
Le rapport entre les températures des photons et des neutrinos après l’annihilation
peut être calculé en utilisant le fait que le système électron–positron-photon reste en
équilibre thermique jusqu’à ce qu’il y reste très peu d’électrons et de positrons ce
qui implique que l’entropie de ce système après et avant l’annihilation soit la même.
Comme nous l’avons trouvé dans la section précédente (6.70), cela implique
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
11 3 3 Tγ a avant = Tγ3 a3 après ,
4
(6.77)
où « avant » et « après » se rapporte à des temps bien avant et bien après l’annihilation électron–positron. Mais après Tg ∼ 1 MeV la température des neutrinos décroît
comme 1/a ce qui implique
[Tν a]après = [Tν a]avant = [Tγ a]avant ,
(6.78)
où dans la dernière étape nous avons fait usage de ce que Tγ = Tν avant l’annihilation
électron–positron. En substituant ceci dans (6.77) on trouve qu’après l’annihilation
électron–positron, les températures des photons et des neutrinos sont reliées par
Tν = (4/11)1/3 Tγ .
(6.79)
U
Q
I
N
Cela correspond à un nombre volumique de neutrinos pour chaque espèce de
nν = (3/11)nγ .
H
C
TE
(6.80)
Le rapport des températures (6.79) se maintient tant que les neutrinos restent
relativistes puisque dans ce cas les températures des photons et des neutrinos décroissent comme a−1 . Si les neutrinos ont des masses suﬃsamment petites mν Tγ (t0 ),
ils sont encore relativistes et ont une température actuelle de
E
L
O
Y
L
PO
Tν (a0 ) = (4/11)1/3 Tγ (a0 ) ∼ 2 Kelvin
3 Nous
ÉC
(si mν 10−4 eV) .
supposons que toute asymétrie neutrino-antineutrino est faible.
(6.81)
E
La nucléosynthèse primordiale
T
Y
L
PO
N
H
EC
E
U
IQ
243
D’autre part, le rapport des densités (6.80) reste le même que les neutrinos demeurent
ou non relativistes si bien que l’on s’attend aujourd’hui à une densité
E
L
O
nν (a0 ) = 1.12 × 108 m−3 .
(6.82)
Une espèce de neutrinos avec m 10−4 eV serait maintenant non-relativiste et
son spectre ne serait pas un spectre thermique car, en l’absence de collisions, la forme
d’un spectre thermique n’est pas conservée pendant l’époque où T ∼ m. Si leur masse
était m > 10 eV ils seraient suﬃsamment lents aujourd’hui pour être piégés dans les
potentiels galactiques et pourraient constituer la matière noire galactique.
ÉC
5
La nucléosynthèse primordiale
E
U
IQ
À des températures et des densités suﬃsamment élevées, les réactions nucléaires
peuvent avoir lieu et il est important pour les cosmologistes de comprendre le mélange
d’éléments produit dans les premiers instants de l’univers. Les premiers calculs ont
été faits par Gamow et ses collaborateurs dans les années 1940 avec l’espoir que l’on
pourrait expliquer l’abondance de tous les éléments. Nous savons que les réactions
nucléaires ont été gelées à T ∼ 30 keV laissant la plupart des noyaux sous forme
d’hydrogène et d’hélium. La nucléosynthèse a recommencé lorsque se sont formées
les étoiles qui ont fourni un « conﬁnement gravitationnel » pour des « réacteure à
fusion » astronomiques.
Dans cette section, nous présentons une brève introduction à la théorie et aux
observations qui la conﬁrment [137]. Le résultat théorique essentiel est de prévoir
l’abondance relative des éléments légers (A ≤ 7, Table 6.3). Sur le plan observationnel, il est très diﬃcile de déterminer les abondances primordiales à cause de la
« pollution » par la nucléosynthèse stellaire. Les meilleures estimations observationnelles sont données dans la Table 6.3. Mis à part 1 H et 4 He, de petites quantités de
2
H, 3 He, 7 Li ont été produites dans l’univers primordial.
Nous verrons que les abondances sont prédites en fonction du rapport baryon/photon
η. Les valeurs calculées sont en accord avec les meilleures observations pour
ÉC
E
L
O
η =
T
Y
L
PO
nb
∼ 5 × 10−10
nγ
⇒
N
H
EC
Ωb h270 ∼ 0.04 .
(6.83)
U
Q
I
N
C’est un résultat très important car il est signiﬁcativement inférieur aux estimations
de la densité totale de matière ΩM ∼ 0.3 ce qui implique l’existence de matière noire
non-baryonique.
Le calcul des abondances primordiales se fait en intégrant les équations de Boltzmann appropriées pour chaque espèce nucléaire. Bien que cela demande à l’évidence
des codes de calcul compliqués, on peut comprendre qualitativement les résultats
parce qu’à haute température la plupart des nucléons sont libres et le restent jusqu’à
une température étonnamment basse, T ∼ 70 keV. La plupart des résultats peuvent
se comprendre en considérant trois époques :
ÉC
E
L
O
Y
L
PO
H
C
TE
E
244
E
U
IQ
Chapitre 6. L’histoire thermique de l’univers
T
Y
L
PO
N
H
EC
Tab. 6.3: Les noyaux importants [129] pour la nucléosynthèse avec leur énergie de liaison par
nucléon, B/A, leur abondance primordiale observée, leur demi-vie et modes de désintégration.
(La demi-vie du 7 Be par capture électronique est donnée pour le bérylium atomique.) On
notera la grande énergie de liaison de 4 He en comparaison avec les autres noyaux légers,
ce qui implique que cette espèce sera le principal produit de la nucléosynthèse primordiale.
L’absence de noyaux stables à A = 5 et A = 8 empêche la production d’éléments lourds par
des réactions à deux corps entre 1 H et 4 He. La nucléosynthèse primordiale s’arrête donc à
A = 7. La production d’éléments lourds se produit dans les étoiles où la réaction triple-α
3 4 He → 12 C peut se produire. On remarque que B/A est une fonction lentement variable
pour A > 12 avec un maximum large à 56 Fe, produit ultime de la nucléosynthèse stellaire.
Les éléments de A > 56 peuvent être produits par la nucléosynthèse « explosive » dans les
supernovae, ou lentement (« processus s ») dans les grosses étoiles où existent de grands
ﬂux de neutrons.
ÉC
E
L
O
noyau
B/A
(MeV)
nx /nH
primordial
(observé)
demi-vie
p
n
0
0
1
0
> 1032 an
10.24 min
1.11
∼ 5 × 10−5
2.83
2.57
0
?
2
H
ÉC
3
E
L
O
T
Y
L
PO
H → 3 He e− ν̄e
3 × 10−22 s
5
Li → p 4 He
∼ 3 × 10−10
0
53.3 jours
e−
7.06
0
6.7 × 10−17 s
8
7.6
8.0
8.7
7.7
0
0
0
0
4
He
7.07
0.08
5
Li
5.27
0
6
Li
5.33
< 10−10
7
7
Li
Be
5.61
5.37
8
Be
C
O
56
Fe
208
Pb
n → pe− ν̄e
3
H
He
16
N
H
EC
12.3 ans
3
12
E
U
IQ
mode de désintégration
ÉC
E
L
O
Y
L
PO
7
Be → νe 7 Li
Be → 4 He 4 He
H
C
TE
U
Q
I
N
E
La nucléosynthèse primordiale
T
Y
L
PO
N
H
EC
E
U
IQ
245
– T > 800 keV. Les neutrons et les protons sont libres et en équilibre chimique ce
qui entraîne
nn
∼ exp(−∆m/T )
np
ÉC
E
L
O
∆m = mn − mp = 1.29 MeV .
(6.84)
L’équilibre chimique est possible à cause des réactions qui transforment les neutrons en protons et vice versa :
νe n ↔ e− p
ν̄e p ↔ e+ n .
(6.85)
La section eﬃcace pour ces interactions faibles est du même ordre de grandeur
que celle de ν ν̄ ↔ e+ e− considérée dans la section précédente. Le taux de
réaction par baryon est donc de l’ordre de :
Γn↔p ∼ G2F T 5
T me , ∆m .
N
H
EC
E
U
IQ
(6.86)
On perd l’équilibre
lorsque le taux de réaction tombe au dessous du taux d’expansion ȧ/a ∼ g(T )T 4/mpl 2 . La température de gel est proche de celle de la
réaction νν ↔ e+ e− :
»
−1
Tg3 ∼
g(1 MeV) G−2
⇒ Tg ∼ 800 keV .
(6.87)
F mpl
E
L
O
T
Y
L
PO
De (6.84) il découle que le rapport neutron-proton à la ﬁn de cette époque est
de l’ordre de
nn
(Tg ) ∼ 0.2
Tg ∼ 800 keV .
(6.88)
np
ÉC
Notons la curieuse « coïncidence » G2F mpl ∆m3 ∼ 1. Cette coïncidence est
responsable du fait que le nombre de neutrons ne soit ni égal ni beaucoup
inférieur au nombre de protons. La conséquence est que la quantité de 4 He
produit est ni plus grande ni beaucoup plus faible que la quantité d’hydrogène.
– 800 keV > T > 60 keV. Les neutrons se désintègrent librement. La durée de cette
période est ∆t = t(60 keV)− t(800 keV) ∼ 3 min (exercice 6.11) si bien qu’à peu
près la moitié des neutrons se désintègrent laissant un rapport neutron-proton
de
nn
(60 keV) ∼ 0.2 exp(−∆t/τn ) ∼ 0.1 .
(6.89)
np
H
C
TE
U
Q
I
N
– T ∼ 60 keV : la nucléosynthèse. Les neutrons restants sont rapidement incorporés dans des noyaux au travers d’une série de réactions, la plus importante
étant :
ÉC
E
L
O
2
H 2H →
Y
L
PO
n p → 2H γ
3
He n
2
H 2H → 3H p
(6.90)
E
246
E
U
IQ
Chapitre 6. L’histoire thermique de l’univers
1
T
Y
L
PO
0.1
0.01
0.001
N
H
EC
0.0001
ÉC
E
L
O
0.1
0.01
T (MeV)
N
H
EC
E
U
IQ
Fig. 6.5: Abondances des éléments légers en fonction de la température pour η = 3 × 10−10
T
Y
L
PO
calculées dans [130]. Les abondances sont négligeables jusqu’à T ∼ 70 keV, après quoi la
plupart des neutrons disponibles sont incorporés dans 4 He. Après T ∼ 30 keV, les réactions
nucléaires sont gelées et les abondances restent constantes en fonction du temps sauf pour
les désintégrations ultérieures de 3 H et 7 Be. Avec la permission d’Elisabeth Vangioni-Flam.
ÉC
E
L
O
3
He 2 H → 4 He p
3
H 2 H → 4 He n
2
H 2 H → 4 He γ .
L’évolution des abondances nucléaires en fonction du temps est montrée sur la
ﬁgure 6.5. Pour η ∼ 5 × 10−10 , pratiquement tous les neutrons sont incorporés
dans 4 He, le noyau léger le plus lié.4 Le nombre de neutrons disponibles (6.89)
détermine donc la quantité d’hélium :
ρHe
2nn /np
=
∼ 0.25
ρH
1 − nn /np
(η ∼ 5 × 10−10 ) .
(6.91)
Deux question se posent à l’évidence sur ce scénario : pourquoi la nucléosynthèse
commence-t-elle si tard (T ∼ 70 keV) ? et pourquoi cesse-t-elle si tôt sans que soient
produits d’éléments lourds ? La première question est particulièrement intéressante car
les énergies de liaison nucléaires sont de quelques MeV et l’on s’attendrait à ce que
les noyaux commencent d’être produits quand T ∼ MeV. La raison de ce démarrage
tardif est le minuscule rapport baryon/photon η ∼ 5×10−10 et son eﬀet sur le premier
processus de la nucléosynthèse, la formation du deutérium par la réaction (6.90). Pour
η ∼ 5 × 10−10 et T ∼ MeV le taux de cette réaction par nucléon est plus grand que
le taux d’expansion (exercice 6.10), D’où il découle qu’il y a un équilibre chimique
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
4 Le noyau le plus solidement lié est abondant non pas parce qu’il est facile à produire, mais parce
qu’il est très diﬃcile à détruire à T ∼ 60 keV.
ÉC
E
La nucléosynthèse primordiale
N
H
EC
E
U
IQ
247
approché entre n , p et 2 H. Dans ces conditions, le taux de formation du deutérium
est égal au taux de sa désintégration par photodissociation :
E
L
O
T
Y
L
PO
np nn σnp vT = n2 nγ σ2γ vT ,
(6.92)
où n2 est le nombre volumique du deutérium. Puisque nγ np , nn , (6.92) ne peut
être satisfait que si n2 np , nn pour compenser le grand nombre de photons. Cette
situation va persister jusqu’à ce que la température soit suﬃsamment faible pour que
σ2γ vT devienne petit parce que très peu de photons ont une énergie supérieure au
seuil de dissociation (2.2 MeV). En utilisant l’équation de Saha, on peut montrer
(exercice 6.10) que n2 np , nn pour T > 70 keV. Puisque les noyaux plus lourds ne
peuvent pas être formés avant que ne soit formé le deutérium, la nucléosynthèse peut
démarrer avant que T atteigne ∼ 70 keV.
Que la ﬁn de la nucléosynthèse soit si proche de son début est dû à deux eﬀets. Le
premier est l’absence d’éléments stables ou métastables de A = 5 ou A = 8 qui rend
impossible la formation de quoi que ce soit par réactions à deux corps de noyaux 4 He
ou 1 H entre eux. Le second est l’eﬃcacité croissante de la barrière coulombienne entre
noyaux chargés qui supprime fortement les sections eﬃcaces pour T < 60 keV. Les
réactions nucléaires gèlent donc à une température de T ∼ 30 keV avec un reliquat
de densité de noyaux qui n’est pas à l’équilibre thermique, caractérisée par l’absence
complète de noyaux lourds.
Comme nous l’avons dit, un des grands intérêts de la théorie de la nucléosynthèse
primordiale est que la comparaison avec les observations permet d’estimer η. Les
abondances prédites en fonction de η sont données sur la ﬁgure 6.6. L’abondance de
4
He, le produit principal de la nucléosynthèse primordiale, est une fonction croissante
de η. Les abondances de noyaux intermédiaires moins liés 2 H et 3 He sont des fonctions décroissantes de η. La raison en est simple. La nucléosynthèse peut se dérouler
seulement si les taux de réactions entre noyaux sont plus importants que le taux d’expansion. Les taux de réactions nucléaires sont proportionnels aux densités de noyaux
dans l’état initial, elles-mêmes proportionnelles à la densité baryonique totale. Pour
la première réaction (6.90), il est facile de montrer (exercice 6.10) que le taux par
nucléon est plus petit que le taux d’expansion pour η < 10−13 ce qui implique qu’il
n’y a essentiellement pas de nucléosynthèse pour η < 10−13 . Pour η > 10−13 , la nucléosynthèse a une eﬃcacité qui croît avec η. Plus précisément, la température du gel
nucléaire est une fonction décroissante de η. Plus le gel est tardif, plus la destruction
des noyaux intermédiaires et la production de 4 He sont eﬃcaces.
On voit sur la ﬁgure 6.6 que pour η ∼ 5 × 10−10 l’abondance de 4 He est assez
insensible à η. C’est parce que la grande majorité des neutrons disponibles sont incorporés dans ce noyau. D’un autre côté, l’abondance de 2 H dépend fortement de η, et
une mesure ﬁable de l’abondance primordiale du deutérium procurerait une mesure
précise de η.
Il est en principe simple de mesurer la quantité de deutérium dans les nuages
intergalactiques en mesurant l’absorption relative des photons émis par les quasars à
grand z par le deutérium et l’hydrogène. La ﬁgure 6.7 montre le spectre d’un quasar
ÉC
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
E
248
E
L
O
1
ÉC
E
U
IQ
Chapitre 6. L’histoire thermique de l’univers
T
Y
L
PO
0.0001
0.001
N
H
EC
0.01
0.1
1
0.1
0.01
0.001
0.0001
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
U
Q
I
N
Fig. 6.6: Abondance des éléments légers en fonction du rapport baryon/photon η supposé
(Axe horizontal du bas) ou de la valeur supposée de Ωb h2 (Axe horizontal du haut), calculée
dans [130]. Pour 4 He, l’abondance est donnée par la fraction Yp = ρHe /ρb de la masse
baryonique totale sous la forme 4 He, alors que pour les autres éléments on donne le nombre
volumique relatif par rapport à celui de 1 H. L’abondance en masse de 4 He est une fonction
lentement croissante de η. Les abondances des noyaux intermédiaires plus faiblement liés 2 H
et 3 He sont des fonctions décroissantes de η. La forme de la courbe de 7 Li est due à ce que
la production est principalement directe pour η < 3 × 10−10 et principalement indirecte par
production et désintégration ultérieure de 7 Be pour η > 3 × 10−10 . Les observations [131]
indiquent que 2 H/1 H ∼ 3.4 × 10−5 dans les nuages intergalactiques de grand redshift. Si cette
ﬁgure reﬂète l’abondance primordiale, on peut conclure que η ∼ 5 × 10−10 ce qui correspond
à Ωb h2 ∼ 0.02 (Ωb h270 ∼ 0.04). Avec la permission d’Elisabeth Vangioni-Flam.
ÉC
E
L
O
Y
L
PO
H
C
TE
E
La nucléosynthèse primordiale
T
Y
L
PO
N
H
EC
E
U
IQ
249
de grand redshift. Du côté bleu de l’émission Lyman-α du quasar, on voit la forêt
de raies correpondant à l’absorption de Ly-α dans les nuages individuels sur la ligne
de visée. L’absorption par un nuage se produit à une longueur d’onde qui satisfait la
condition λ1 /λLyα = (znuage + 1)/(zquasar + 1). Le problème est de trouver un nuage
dont la profondeur optique permette d’observer l’absorption à la fois de l’hydrogène et
du deutérium. Dans ce spectre, un tel nuage apparaît avec une absorption à 555.8 nm
pour l’hydrogène. L’ absorption est totale au centre de la raie de l’hydrogène, mais la
quantité d’hydrogène dans le nuage peut être estimée à partir de la largeur du proﬁl
d’absorption. La raie d’absorption du deutérium est également visible et la quantité
de deutérium peut être estimée à partir de l’absorption totale de cette raie. Le spectre
montre que seuls les nuages de profondeur optique située dans une plage assez étroite
peuvent être utilisés pour mesurer le rapport deutérium-hydrogène. La mesure est
impossible dans des nuages avec moins d’absorption (ce qui rend la raie du deutérium
trop faible pour être observée) ou pour des nuages avec plus d’absorption (ce qui fait
que l’élargissement de la raie de l’hydrogène empiète sur celle du deutérium).
Seule une poignée de systèmes d’absorption ont été trouvés dans les spectres des
quasars. Les trois meilleurs exemples donnent des résultats compatibles avec [131] :
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
n2 /n1 = (3.4 ± 0.3) × 10−5 .
(6.93)
La quantité d’éléments lourds dans ces trois nuages de grand redshift est très
faible (∼ 10−3 de l’abondance dans le Soleil) Ce qui laisse à penser que l’abondance
du deutérium ne serait pas perturbée par la nucléosynthèse stellaire. Si l’on suppose
que (6.93) reﬂète l’abondance primordiale, la théorie de la nucléosynthèse donne une
valeur précise de η et Ωb :
ÉC
E
L
O
η ∼ (5.1 ± 0.3) × 10−10
⇒
Ωb h270 = 0.039 ± 0.002 .
(6.94)
Comme c’est souvent le cas en astrophysique, l’erreur donnée est très formelle car
l’incertitude réelle provient des hypothèses nécessaires pour interpréter les données.
Ici, il est nécessaire de supposer que les deux raies de la ﬁgure 6.7 près de 555.8 nm
sont correctement identiﬁées et de supposer que les abondances mesurées sont des
abondances primordiales. Si l’une de ces hypothèses est fausse, on doit réinterpréter
la mesure. Par exemple, la raie du « deutérium » pourrait être une raie de l’hydrogène
d’un autre nuage de redshift légèrement diﬀérent. Cela produirait une surestimation
du deutérium par les observateurs et une sous-estimation de Ωb . D’un autre côté, si
le deutérium n’est pas primordial, le deutérium primordial est sous-estimé puisque les
processus stellaires détruisent en général le deutérium. Cela causerait une surestimation de Ωb .
Il est clair que la valeur de η obtenue à partir de l’abondance du deutérium demande des conﬁrmations par des expériences indépendantes. Les abondances mesurées
de 4 He et 7 Li (Fig. 6.8) donnent des conﬁrmations qualitatives bien qu’une certaine
controverse subsiste [137]. La quantité totale de gaz dans la forêt Ly-α donne une
limite inférieure pour Ωb cohérente avec la valeur de la nucléosynthèse [138]. Nous
verrons au chapitre 7 que les spectres des anisotropies du CBR [25] des données de
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
250
ÉC
E
U
IQ
Chapitre 6. L’histoire thermique de l’univers
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
T
Y
L
PO
N
H
EC
E
U
IQ
H
C
TE
U
Q
I
N
Fig. 6.7: Spectre d’un quasar qui montre l’émission Ly-α à 580 nm et, du côté bleu, la
« forêt » de raies d’absorption Ly-α par des nuages de gaz sur le chemin [131]. Le zoom
sur la gauche montre l’absorption Ly-α d’hydrogène et de deutérium par un seul nuage. La
raie du deutérium est déplacée par rapport à celle de l’hydrogène par eﬀet de masse réduite
électron-noyau. Le rapport entre l’absorption par l’hydrogène et par le deutérium peut être
utilisé pour déterminer leur abondance dans le nuage. Avec la permission de D. Tytler.
ÉC
E
L
O
Y
L
PO
E
La nucléosynthèse primordiale
T
Y
L
PO
0.01
0.26
ÉC
E
L
O
0.24
N
H
EC
E
U
IQ
251
0.22
0.2
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
U
Q
I
N
Fig. 6.8: Abondances des éléments légers calculées en fonction du rapport baryon/photon
η dans l’intervalle 10−10 < η < 10−9 [130]. Les lignes horizontales ponctuées montrent
les domaines permis par les observations. Comme on l’explique dans le texte, l’abondance
de 2 H dans les nuages intergalactiques peut être mesurée au travers de son absorption de
la lumière émise par les objets du fond cosmique. Les mesures motrées ici [132] donnent
2
H/1 H ∼ 3.4 × 10−5 ce qui implique η ∼ 5 × 10−10 . D’autres mesures [133] donnent 2 H/1 H ∼
2 × 10−4 ce qui implique η ∼ 1.5 × 10−10 . L’abondance de 4 He peut être mesurée par les
raies de recombinaison de l’hélium dans les région fortement ionisées « HII » entourant
les étoiles chaudes. Les mesures donnent une fraction de masse d’hélium, Yp , entre ∼ 0.23
[134] et ∼ 0.25 [135]. L’abondance du lithium est estimée à partir des raies d’absorption
dans les étoiles avec de faibles abondances d’éléments lourds. Ces mesures [136] donnent
7
Li/1 H ∼ 2 × 10−10 . Toutes les mesures sont compatibles avec 1.5 × 10−10 < η < 6 × 10−10 .
ÉC
E
L
O
Y
L
PO
H
C
TE
E
252
E
U
IQ
Chapitre 6. L’histoire thermique de l’univers
T
Y
L
PO
N
H
EC
Maxima et Boomerang donnent des valeurs de Ωb en accord avec la valeur déduite de
la nucléosynthèse primordiale.
6
ÉC
E
L
O
Wimps
Les trois espèces connues de neutrinos étaient relativistes quand elles se sont découplées (Tg mν ). Une conséquence est qu’aujourd’hui le nombre volumique de
neutrinos est du même ordre que celui des photons nν = (3/11)nγ . Si l’un de ces neutrinos était suﬃsamment massif pour être non-relativiste aujourd’hui, sa densité de
masse actuelle serait ρν = mν nν . Cela donne ΩM ∼ 0.3 pour une masse du neutrino
de l’ordre de 10 eV.
N’importe quelle particule stable hypothétique avec m > 10 eV qui s’est découplée
lorsqu’elle était relativiste créerait des problèmes pour la cosmologie car la densité de
masse calculée serait sur-critique. Une particule lourde interagissant faiblement peut
donner une densité cosmologique appropriée seulement si sa section eﬃcace d’annihilation est suﬃsamment grande pour la maintenir en équilibre jusqu’à ce que la particule
soit non-relativiste, Tg m. Dans ce cas, son nombre volumique serait diminué par le
facteur de Boltzmann, et la densité actuelle pourrait ne pas être trop grande. De fait,
si la section eﬃcace est choisie correctement, la particule peut donner un reliquat de
densité près de la valeur critique et constituer ainsi la matière noire non-baryonique
souhaitée.
Une telle compensation entre le reliquat de densité et la masse semble a priori
improbable, mais des choses bien plus étranges sont arrivées en cosmologie. De fait,
il se trouve que les particules avec des interactions faibles et des masses de l’ordre du
GeV donnent de façon naturelle des reliquats de densité qui ne sont éloignées que de
quelques ordres de grandeur ou moins de la valeur critique. De telles particules sont
appelées des « wimps » pour « weakly interacting massive particle ». Numériquement, on trouve que
ÉC
E
L
O
T
Y
L
PO
Ωwimp h270 ∼
N
H
EC
E
U
IQ
1.4 × 10−37 cm2
.
σv/c
(6.95)
Le reliquat de densité est inversement proportionnelle à la section eﬃcace d’annihilation. C’est raisonnable puisque plus la section eﬃcace est élevée, plus les particules
sont détruites dans l’univers primordial.
L’existence d’un wimp stable est prédit par les extensions supersymétriques du
modèle standard de la physique des particules. La particule est appelée « LSP »
(lightest supersymmetric particle) et notée χ. Les wimps supersymétriques sont habituellement des particules de « Majorana », c’est-à-dire qu’elles sont leurs propres
antiparticules. Les théories supersymétriques ont beaucoup de paramètres qui ne sont
pas, pour le moment, ﬁxés par l’expérience. On peut en général choisir des paramètres
qui donnent la section eﬃcace voulue pour obtenir un reliquat de densité voulu. Le
fait que ces particules n’aient pas été vues dans les accélérateurs signiﬁe que très pro-
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Wimps
T
Y
L
PO
N
H
EC
E
U
IQ
253
bablement mχ > 30 GeV [62]. La recheche de wimps piégés dans le halo galactique a
été discutée dans la section 4.
Pour comprendre (6.95), il nous faut considérer l’équation de Boltzmann pour nχ :
ÉC
E
L
O
dnχ a3
Γχχ→x nχ (T )2 − n2χ
=
1/3
,
da3
ȧ/a
nχ
(6.96)
où Γ = nχ σv est le taux d’annihilation.
Comme avec les électrons et les positrons, une solution approximative de (6.96)
est
nχ ∼ nχ (T )
T Tg
nχ a3 ∼ constante
T Tg ,
N
H
EC
(6.97)
E
U
IQ
(6.98)
où Tg est la température de gel correspondant au moment où le taux d’annihilation
a été le même que le taux d’expansion :
T
Y
L
PO
»
Tg2
8πg(Tg )/3
.
mpl
nχ (Tg ) σv = H(Tg ) =
E
L
O
(6.99)
La solution numérique est montrée pour trois valeurs de la section eﬃcace sur
la ﬁgure 6.9. On voit qu’en raison de la dépendance exponentielle de nχ (T ) pour
T < mχ , la température de gel est relativement insensible à la valeur de la section
eﬃcace, Tg ∼ mχ /20. On peut donc facilement estimer le reliquat de densité de χ en
égalant le taux d’annihilation et le taux d’expansion. Cela donne :
g(Tg )
nχ (ag )
nχ (ag )
∼
∼
.
(6.100)
3
nγ (ag )
Tg
σv mpl mχ /20
ÉC
Après le gel, l’expansion est adiabatique séparément pour les wimps et pour les
particules en équilibre thermique :
Å
nχ (a0 ) = nχ (ag )
Ç
nγ (a0 ) = nγ (ag )
ce qui donne
E
L
O
ï
ÉC
nχ
nγ
ag
a0
ã3
gg a3g
g0 a30
å
Y
L
PO
ï
ò
=
0
nχ
nγ
ò
f
U
Q
I
N
(6.101)
g0
.
gg
H
C
TE
,
(6.102)
(6.103)
E
254
ÉC
E
U
IQ
Chapitre 6. L’histoire thermique de l’univers
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
T
Y
L
PO
N
H
EC
E
U
IQ
Fig. 6.9: log(nχ /nγ ) en fonction de la température pour trois valeurs de la section eﬃcace
d’annihilation σv/c. La masse choisie des wimps est mχ = 50 GeV. La ligne pointillée montre
log(nχ /nγ ) en équilibre thermique. Le gel se produit vers Tg ∼ mχ /20 où g(Tg ) ∼ 50. On
voit qu’en bonne approximation le reliquat de densité est inversement proportionnel à la
section eﬃcace. En utilisant (6.103), il est facile de montrer que Ωwimp est proche de 1 pour
σv ∼ 10−37 cm2
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Baryogénèse
T
Y
L
PO
N
H
EC
E
U
IQ
255
En combinant avec (6.100) on obtient le nombre volumique de wimps actuel
ï ò
nχ g 0
nγ (a0 )
.
(6.104)
nχ (a0 ) ∼
nγ (a0 ) ∼ nγ f g g
g(Tg ) σv mpl mχ /20
ÉC
E
L
O
En multipliant par mχ , on voit que le reliquat de densité ρχ = mχ nχ est inversement
proportionnel à la section eﬃcace avec une faible dépendance en mχ à cause du facteur
gg = g(Tg ). Divisant par la densité critique, on trouve numériquement (6.95).
7
Baryogénèse
Nous avons calculé les rapports nν /nγ et nχ /nγ avec l’équation de Boltzmann et
l’on pourrait aussi espérer calculer le rapport
η=
nb − n̄b
nb
=
∼ 5 × 10−10 .
nγ
nγ
N
H
EC
E
U
IQ
(6.105)
Ce problème est fondamentalement diﬀérent des deux autres. Pour les neutrinos et
les wimps, nous avons supposé que le nombre de particules est égal au nombre d’antiparticules, c’est-à-dire que nous avons supposé que le potentiel chimique est nul. Pour
calculer η, le problème est de calculer l’asymétrie ou le potentiel chimique.
Bien entendu, l’asymétrie baryon-antibaryon peut être considérée comme étant une
simple condition initiale. Si le nombre baryonique est conservé, cette asymétrie sera
conservée. Néanmoins, les arguments de symétrie sont très séduisants et les physiciens
ont envisagé la possibilité qu’à grande échelle il n’y ait pas d’asymétrie. L’asymétrie
locale serait soit une ﬂuctuation statistique ou le résultat de quelque mécanisme hypothétique qui aurait séparé les baryons et les antibaryons. Malheureusement, aucun
scénario plausible n’a été trouvé.
Depuis l’invention des théories de grande uniﬁcation de la physique des particules
dans les années 1970, les physiciens se sont penchés sur des mécanismes qui peuvent
créer une asymétrie globale en commençant avec des conditions initiales symétriques.
Les trois conditions nécessaires pour réaliser cela ont été identiﬁées par Sakharov (dans
les années 1960). Pour créer une asymétrie, il est certainement nécessaire qu’il existe
des interactions qui ne conservent pas le nombre baryonique, ce qui est généralement le
cas dans les théories GUT. Cependant, comme nous l’avons vu dans la section 2, si les
interactions ont lieu à l’équilibre thermique, elles détruisent plus qu’elles ne favorisent
une asymétrie. La deuxième condition est par conséquent que les réactions avec nonconservation du nombre baryonique se produisent hors de l’équilibre. Cette condition
peut être réalisée à cause de l’expansion de l’univers. Enﬁn, on remarque que si les
événements individuels violent la conservation du nombre baryonique, on ne peut pas
créer globalement une asymétrie si l’on ne favorise pas la production de baryons par
rapport aux antibaryons. Nous verrons sur un exemple particulier (exercice 6.9) que
cela peut être réalisé si les interactions qui ne conservent pas le nombre baryonique
violent également « C » et « PC », c’est-à-dire la symétrie de conjugaison de charge
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
256
E
U
IQ
Chapitre 6. L’histoire thermique de l’univers
T
Y
L
PO
N
H
EC
et le produit de la conjugaison de charge par la symétrie d’inversion d’espace (parité).
L’opération de conjugaison de charge change les particules en antiparticules (et vice
versa) et l’opération de parité renverse toutes les coordonnées spatiales.
Dans les GUT, les interactions qui violent le nombre baryonique sont transmises
par l’échange de bosons super-lourds M > 1015 GeV. Cela explique la stabilité apparente du proton τp > 1032 an. Dans ces théories, l’asymétrie provient de la désintégration asymétrique de particules lourdes à très haute température T ∼ 1015 GeV. Un
modèle particulier est traité dans l’exercice 6.9.
En réalité, les choses sont un peu plus compliquées parce qu’il a été découvert que
les théories de jauge des interaction de (relativement) basse énergie que l’on observe
(comme le modèle standard des particules et interactions fondamentales, avec ou
sans supersymétrie) contiennent des eﬀets subtils qui violent le nombre baryonique
au travers d’un eﬀet tunnel non-perturbatif entre des états dégénérés du vide [139].
Ainsi, on s’attend à une violation du nombre baryonique à des températures T ∼ mW .
Si ces interactions se produisent à l’équilibre thermique, elles peuvent détruire une
asymétrie préexistante. Si elles ne se produisent pas à l’équilibre thermique, elles
peuvent en créer une nouvelle.
Ce qui se passe exactement dépend de la nature de l’asymétrie créée par les interactions GUT et de la nature de la violation du nombre baryonique par les interactions
électro-faibles. Selon le type de théorie grand-uniﬁée, les interactions à la température GUT peuvent ou non produire une asymétrie du nombre leptonique, par exemple
ne− + nνe = ne+ + nν̄e , et le sort de l’asymétrie baryonique dépend de l’asymétrie
leptonique. Par exemple, dans le modèle standard de la physique des particules sans
supersymétrie les interactions à T ∼ mW annulent la somme des nombres baryonique et leptonique (B + L), alors qu’elles conservent leur diﬀérence (B − L). Si les
interactions GUT interactions ﬁxent B − L = 0, alors B est amené à zéro par les
interactions électrofaibles. Si l’on ajoute la supersymétrie au modèle standard, les
asymétries seront traitées d’une façon qui dépend des paramètres et des symétries du
modèle.
Pour réellement progresser dans cette direction, il serait certainement souhaitable
et bénéﬁque d’avoir de l’information expérimentale supplémentaire sur la physique
GUT ainsi que sur la physique électrofaible.
ÉC
E
L
O
ÉC
8
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
L’irréversibilité
H
C
TE
U
Q
I
N
Nous avons vu que dans un univers homogène la densité d’entropie évolue selon
(6.23) :
Y
L
PO
µi dni a3
dsa3
= −
,
3
da
T da3
i
E
L
O
(6.106)
où la somme porte sur toutes les espèces de particules. Cette équation remarquable
nous dit que l’entropie peut croître seulement par la création ou la destruction de
ÉC
E
L’irréversibilité
T
Y
L
PO
N
H
EC
E
U
IQ
257
particules hors de l’équilibre thermique. Sans création ou destruction de particules,
ni a3 est constant pour chaque espèce et chaque terme de (6.106) s’annule. À l’équilibre
thermique, la condition pour qu’il y ait équilibre chimique (6.46) impose que la somme
s’annule pour toutes les réactions.
Dans un univers inhomogène, il existe d’autres façons d’accroître l’entropie. On
pense immédiatement à la diﬀusion de chaleur ou de particules entre des zones de
température ou de densité diﬀérente. Un moyen encore plus eﬃcace pour accroître
l’entropie est au travers de la formation de structures gravitationnellement liées. Ce
processus a pour conséquence de rayonner des photons (exercice 2.10). Puisque l’entropie est proportionnelle au nombre de particules, ce processus accroît directement
l’entropie.
Dans l’univers primordial, il y avait peu d’exemples de processus produisant de
l’entropie. L’un, que nous avons déjà vu, est la désintégration libre de particules, par
exemple la désintégration du neutron pendant la période 800 keV > T > 60 keV. Le
deuxième exemple que nous considérons ici est l’annihilation particule-antiparticule
près de la température de gel T ∼ Tg .
Revenons par conséquent sur le cas d’un wimp de Majorana (χ = χ̄) considéré
dans la section 6. En substituant l’équation de Boltzmann pour les wimps (6.96) dans
(6.106), nous trouvons
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
dsa3
µχ σv
(nχ (T )2 − n2χ ) .
= −
3
da
T 3ȧ/a
ÉC
E
L
O
(6.107)
Pour T > Tg , les χ sont presque en équilibre thermique, nχ ∼ nχ (T ) et l’équation
de Boltzmann (6.96) donne donc
3ȧ/a dnχ a3 (6.108)
nχ ∼ nχ (T ) +
T > Tg ⇒ Γ > ȧ/a .
2Γ da3 On voit que nχ est un petit peu plus grand que la valeur à l’équilibre. L’excès est dû à
ce que les χ ne peuvent pas s’annihilier suﬃsamment vite pour suivre la décroissance
rapide de l’abondance à l’équilibre.
L’excès de χ donné par (6.108) est équivalent à un potentiel chimique :
3ȧ/a 1 dnχ a3 µχ =
(6.109)
T > Tg ⇒ Γ > ȧ/a .
2Γ nχ da3 La dérivée de l’entropie est donc
2
dsa3
3ȧ/a 1 dnχ a3 ∼
da3
2Γ nχ da3 H
C
TE
T > Tg ⇒ Γ > ȧ/a .
Y
L
PO
U
Q
I
N
(6.110)
En approximant nχ par sa valeur à l’équilibre, on trouve
E
L
O
dsa3
ȧ/a m2
∼
da3
6σv T 2
ÉC
mχ > T > T g .
(6.111)
E
258
E
U
IQ
Chapitre 6. L’histoire thermique de l’univers
N
H
EC
Le membre de droite de cette équation est constant dans la mesure où ȧ/a ∝ T 2 .
Dans cette approximation, on peut remplacer toutes les quantités par leur valeur à
T = Tg :
ÉC
E
L
O
T
Y
L
PO
dsa3
nχ (Tg ) m2
∼
da3
6
Tg2
mχ > T > T g ,
(6.112)
où nous avons utilisé ȧ/a = Γ à T = Tg . En intégrant cette équation, on trouve
l’entropie engendrée pendant la période d’annihilation :
ã
Å
mχ 2 n χ ∆sa3
∼
T g < mχ .
(6.113)
sa3
Tg
s Tg
En se reportant à la ﬁgure 6.9, on voit que l’annihilation d’un wimp de masse mχ ∼
50 GeV et de section eﬃcace d’annihilation σv/c ∼ 10−37 cm2 aura une température
de gel de mχ /Tg ∼ 20 et un reliquat de densité de nχ /s = nχ /gnγ ∼ 10−10 . La
quantité d’entropie engendrée au moment du gel est donc ∆sa3 /sa3 ∼ 10−8 .
La manifestation immédiate de l’augmentation d’entropie serait la diminution par
le même facteur du rapport entre le nombre volumique de baryons et le nombre volumique de particules relativistes, nrel . Cela se produit parce que le nombre baryonique
est conservé avec grande précision (nb a3 = constante) alors que le nombre de particules relativistes suit l’entropie qui n’est pas conservée (nrel a3 ∼ sa3 = constante).
Une conséquence plus dramatique de l’augmentation d’entropie est que l’expansion
n’est pas réversible. Cela implique que l’époque de contraction d’un univers fermé n’est
pas une époque d’expansion renversée dans le temps. La ﬁgure 6.10 montre l’évolution
du rapport nχ /nγ pendant ces deux époques. Après le gel dans l’époque d’expansion,
l’annihilation continue pendant un temps court sans qu’il y ait compensation par la
réaction inverse. Pendant l’époque de contraction, l’annihilation recommence avant
que l’augmentation de température au point où la production thermique des χ puisse
commencer. Un ﬁlm de la phase de contraction n’est pas, par conséquent, le même que
le ﬁlm de la phase d’expansion passé à l’envers puisque pendant une courte période
pendant la contraction nχ décroît alors que la température croît. Dans le ﬁlm de
l’expansion passé à l’envers, nχ augmente toujours lorsque la température augmente.
ÉC
9
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
Le futur
U
Q
I
N
L’activité thermique actuelle de l’univers est dominée par la production de photons, de neutrinos et de noyaux lourds dans les réactions de fusion nucléaire dans
les étoiles. Les photons s’échappent des surfaces stellaires dans l’espace alors que les
neutrinos produits dans la fusion de l’hydrogène en hélium s’échappent directement
des cœurs stellaires. Les neutrinos et les photons « chauds » s’ajoutent donc aux
neutrinos et photons froids primordiaux et produisent un mélange hors d’équilibre.
Pendant quelques temps de Hubble on verra se poursuivre ces processus. La formation cosmologique de structures a cessé (ou va cesser) lorsque ΩM descend signiﬁcativement au dessous de 1, ce qui ﬁxe la quantité de matériau disponible pour la
ÉC
E
L
O
Y
L
PO
H
C
TE
E
Le futur
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
T
Y
L
PO
E
U
IQ
N
H
EC
259
E
U
IQ
Fig. 6.10: log(nχ /nγ ) en fonction de la température pour mχ = 50 GeV et σv/c =
10−37 cm2 . La ligne continue correspond à la phase d’expansion et la ligne pointillée à la
phase de contraction d’un univers fermé.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
260
E
U
IQ
Chapitre 6. L’histoire thermique de l’univers
T
Y
L
PO
N
H
EC
formation des étoiles. Les étoiles lourdes peuvent recycler leur matériau par des explosions de supernovae mais on peut penser qu’après un certain temps, la plus grande
partie de la matière baryonique se retrouvera dans des étoiles de faible masse. Après
avoir brûlé l’hydrogène de leur cœur, ces étoiles se refroidiront tout simplement. Dans
un certain nombre de temps de Hubble, on peut donc s’attendre à ce que l’univers
consistera en des particules extragalactiques et en des galaxies constituées de matière
noire non-baryonique et des étoiles mortes, c’est-à-dire des naines blanches, des naines
brunes, des étoiles à neutrons et des trous noirs. On peut s’attendre à ce que la masse
galactique soit de plus en plus concentrée dans des trous noirs massifs au centre des
galaxies puisque ces objets provoquent une accrétion de la matière environnante.
Si l’univers évite une époque de contraction, comme le suggère la mesure actuelle
de ΩΛ , le futur lointain sera déterminé par des processus plus exotiques. Le futur
est simple si le proton est instable comme le prévoient beaucoup d’extensions du
modèle standard de la physique des particules. La désintégration du proton produira
de plus en plus de photons, de neutrinos et de positrons. Les positrons venant de
désintégrations dans les étoiles vont immédiatement s’annihiler. Après quelques durées
de vie du proton, les étoiles mortes se seront évaporées à cause de la désintégration
du proton. Les positrons produits dans des désintégrations intergalactiques seront
protégés de l’annihilation par l’expansion de l’univers avec Γ H.
Les dernières structures survivantes seront des trous noirs, mais ceux-ci vont aussi
s’évaporer par rayonnement de Hawking. Après cela, l’univers consistera dans le CBR
original et des neutrinos, de divers mélanges non-thermiques de particules stables, et,
probablement, d’une énergie du vide qui dominera l’énergie totale. Ce qui se passera
après dépendra de la nature inconnue de l’énergie du vide. Comme exemple, notons
que la dernière fois que l’univers a été dominé par l’énergie du vide est pendant
l’inﬂation. Cette période s’est terminée par une transition de phase qui a été le début
de l’époque de la domination des particules.
ÉC
E
L
O
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
Exercices
6.1 Considérons un système de particules identiques en équilibre thermique à une
température T avec un potentiel chimique µ. La distribution dans l’espace des phases
est donnée par (6.10).
(a) Veriﬁer les formules de l’équilibre thermique de la Table 1.
(b) L’utilisation de formules du gaz parfait pour un gaz de particules chargées est
justiﬁée seulement si l’énergie cinétique moyenne des particules est beaucoup plus
grande que l’énergie potentielle moyenne due aux interactions coulombiennes. Pour
un gaz globalement neutre, l’énergie potentielle est de l’ordre de U ∼ e2 n1/3 où n est
le nombre volumique des particules chargées. Comparer les deux énergies pour un gaz
de paires électron–positron à la température T me et pour T me .
(c) À l’équilibre thermique, si la densité de particules n(T ) n’est pas égale à la densité
d’antiparticules n̄(T ) leur potentiel chimique ne s’annule pas, µ = −µ̄ = 0. Calculer
n(T, µ) − n̄(T, −µ) dans la limite (T m, T µ). Estimer le potentiel chimique des
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Exercices sur le chapitre 6
N
H
EC
E
U
IQ
261
électrons et des positrons dans notre univers pour T me .
(d) Après le gel, T < Tg me , il n’y a plus d’annihilations électron–positron et les
densités sont ﬁxées à ne ∼ 4 × 10−10 nγ et n̄e ∼ 0. En l’absence d’annihilations, on ne
peut plus supposer µ = −µ̄. Estimer la valeur de µe pour T Tg .
ÉC
E
L
O
T
Y
L
PO
6.2 Considérons un gaz parfait dans un volume V d’énergie totale E et comportant
N particules. La température T , la pression p et le potentiel chimique µ sont déﬁnis
de façon que la diﬀérentielle de l’entropie S soit donnée par
dS =
dE
pdV
µdN
+
−
.
T
T
T
Utiliser cette relation pour montrer que la densité d’entropie s(T, µ) est donnée par
s(T, µ) =
ρ(T, µ) + p(T, µ) − µn(T, µ)
T
T
Y
L
PO
N
H
EC
E
U
IQ
6.3 Démontrer l’équation de Liouville pour des particules massives (6.26) en modiﬁant de façon appropriée les ﬁgures 1.10 et 1.11.
E
L
O
6.4 Considérons une réaction i + j → k + l avec un taux
ÉC
Γij→kl = nj σv ,
(6.114)
où σv est la moyenne de la section eﬃcace multipliée par la vitesse.
Considérons un temps t1 après legel lorsque le taux de réaction est signiﬁcativement moindre que le taux d’expansion
Γ(t1 ) H(t1 ) .
(6.115)
On suppose qu’après t1 le nombre de particules j est conservé : nj ∝ a−3 et que la
section eﬃcace a une forme simple : σv ∝ T β ∝ a−β ( β = 0 pour l’annihilation
électron–positron et pour la diﬀusion Thomson). Intégrer le taux de réaction pour
montrer que la réaction est véritablement gelée :
∞
∞
Γdt =
Γda/ȧ 1 ,
(6.116)
t1
a1
Y
L
PO
H
C
TE
U
Q
I
N
c’est-à-dire que la plupart des particules i ne vont jamais être à nouveau diﬀusées.
E
L
O
6.5 L’énergie de liaison de l’état fondamental de l’hydrogène atomique est B =
13.6 eV et pour T < B on s’attendrait à ce que les électrons se « recombinent » avec
les protons pour former des atomes. Parce que la section eﬃcace pour la diﬀusion
ÉC
E
262
E
U
IQ
Chapitre 6. L’histoire thermique de l’univers
T
Y
L
PO
N
H
EC
photon-hydrogène est moindre que celle de la diﬀusion photon-électron, la recombinaison précipite le découplage de la matière et des photons ce qui rend l’univers
eﬀectivement transparent.
Dans cet exercice, nous allons estimer la température à laquelle l’univers devient
transparent, et le nombre d’électrons qui restent non-liés. Pour le faire, nous aurons
besoin de connaître la fraction d’électrons en équilibre thermique et la section eﬃcace
de formation d’atomes.
Pour simpliﬁer le problème, nous allons considérer seulement l’état fondamental
de l’hydrogène atomique. Dans ce cas, à l’équilibre thermique les densités d’électrons,
de protons et d’atomes d’hydrogène sont reliées par l’équation de Saha :
Å
Å
ã
ã
2π 2π mH T 3/2 B/T
2π 3/2 B/T
nH
=
e
∼
e
np ne
me T mp T 2π
me T
ÉC
E
L
O
E
U
IQ
(a) Démontrer l’équation de Saha en utilisant µe + µp = µH à l’équilibre thermique.
En négligeant la présence de l’hélium, on peut écrire :
N
H
EC
ne = np = xnb = xηnγ
T
Y
L
PO
nH = (1 − x)ηnγ ,
où η = nb /nγ ∼ 5×10−10 et x est la fraction d’ionisation. L’équation de Saha devient :
ÉC
E
L
O
2.4
1−x
= η 2
x2
π
Å
2πT
me
ã3/2
eB/T .
On voit que puisque η 1, la température doit être signiﬁcativement inférieure à
l’énergie de liaison B avant que la densité d’atomes devienne appréciable. Il s’ensuit
que la recombinaison se produit bien plus tard qu’on ne s’y serait attendu naïvement.
C’est la même situation que celle rencontrée dans la section 5 où nous avons trouvé
que la formation de noyaux commence seulement à T ∼ 60 keV, c’est-à-dire bien au
dessous de l’énergie de liaison du deutérium. L’explication est que la densité de photons était si grande que le deutérium (ou l’hydrogène atomique) a été photo-dissocié
rapidement, même pour des températures bien inférieures à l’énergie de liaison.
L’équation de Saha s’applique seulement dans le cas de l’équilibre thermique qui
demande que le taux de recombinaison soit plus grand que le taux d’expansion. La
section eﬃcace pour la formation de l’état fondamental de l’hydrogène atomique est
σrec (e− p → Hγ) = 4π
H
C
TE
α2 B
.
m2e mv 2
Y
L
PO
U
Q
I
N
En multipliant par la vitesse et en moyennant √
sur le spectre thermique on obtient un
taux de réaction inversement proportionnel à T :
Å
ã
1 eV 1/2
10−13 cm3 s−1 .
σrec v = 1.4
T
ÉC
E
L
O
E
Exercices sur le chapitre 6
T
Y
L
PO
N
H
EC
E
U
IQ
263
Le taux de recombinaison est alors ce facteur multiplié par la densité de protons,
Γrec = np σrec v
La transparence de l’univers est déterminée par le taux de diﬀusion. Deux processus doivent être considérés : la diﬀusion Thomson sur des électrons libres et la diﬀusion
Rayleigh sur des atomes. La section eﬃcace de diﬀusion Rayleigh est de l’ordre de
σR = σT (Eγ /B)4 où σT = 6.65 × 10−25 cm2 est la section eﬃcace Thomson. Le taux
de diﬀusion des photons est donc
Å ã4
T
c.
(6.117)
ΓT + ΓR ∼ ne σT c + nH σT
B
ÉC
E
L
O
(b) Pour une série de températures entre 0.3 eV et 0.2 eV calculer le taux d’expansion
H(T ), la fraction d’hydrogène ionisé à l’équilibre x(T ), et les taux à l’équilibre ΓR (T ),
ΓT (T ) et Γrec (T ). On peut supposer ΩM = 0.3 et η = 5 × 10−10 .
(c) Estimer la température lorsque ΓT + ΓR devient inférieur à H(T ). C’est la température à laquelle l’univers devient transparent aux photons.
(d) Estimer la température lorsque le taux de recombinaison devient inférieur au taux
d’expansion. Quelle fraction d’hydrogène reste ionisée ?
T
Y
L
PO
N
H
EC
E
U
IQ
6.6 Les photons de la réaction e+ e− → γγ sont hautement non-thermiques pour des
annihilations tardives T me . Dans la diﬀusion Thomson avec Eγ me , un photon
perd en moyenne une fraction ∼ Eγ /me de son énergie. Estimer le nombre de collisions nécessaires pour qu’un photon d’annihilation atteigne une énergie thermique.
Comparer le temps nécessaire à la thermalisation avec le temps de Hubble de l’époque
appropriée.
ÉC
E
L
O
6.7 Estimer la température de gel pour l’annihilation des positrons dans un univers
avec ne /nγ ∼ 4 × 10−10 . Estimer le reliquat de densité de positrons.
6.8 Les neutrinos (antineutrinos) produits dans les interactions faibles normales ont
des hélicités gauches (droites). Si les neutrinos sont des particules de « Dirac », les
neutrinos et antineutrinos de la « mauvaise » hélicité existent mais ils ont des section
eﬃcaces inférieures à celles des neutrinos normaux par un facteur ∼ m2ν /Eν2 . Montrer
que les neutrinos de la mauvaise hélicité et de masse inférieure à ∼ 10 keV n’atteignent
jamais l’équilibre thermique.
H
C
TE
U
Q
I
N
6.9 Dans cet exercice, nous étudions un modèle [140] de baryogénèse reposant sur
certaines idées des théories de grande uniﬁcation (GUT). On suppose l’existence d’un
boson super-lourd X de charge 4/3 et son antiparticules X̄ avec mX 1 TeV. On suppose qu’initialement l’univers est symétrique, nX = n̄X , et que les X se sont découplés
des autres particules de telle sorte que leurs seules interactions sont des désintégrations libres de vie moyenne τ . Un théorème fondamental de la physique des particules
ÉC
E
L
O
Y
L
PO
E
264
E
U
IQ
Chapitre 6. L’histoire thermique de l’univers
T
Y
L
PO
N
H
EC
(conservation de CPT) implique que les vies moyennes de X et X̄ sont égales, τ = τ̄
(voir ci-dessous).
Pour simpliﬁer les choses, nous supposons qu’il n’y a que deux modes de désintégration du X, qui produisent tous deux des quarks u ou d ou les antiquarks
correspondants :
ÉC
E
L
O
X → uu
rapport de branchement = r
rapport de branchement = 1 − r .
X → d̄e+
Les modes de désintégration de X̄ sont
X̄ → ūū
rapport de branchement = r̄
X̄ → de−
E
U
IQ
rapport de branchement = 1 − r̄ .
N
H
EC
Si les symétries « C » et « CP » sont violées, on peut avoir r = r̄ (voir ci-dessous).
(a) Le nombre baryonique des quarks u et d est 1/3 et celui des antiquarks −1/3.
Quel est le nombre baryonique moyen engendré à par désintégration de X et par
désintégration de X̄ ?
(b) On suppose que les désintégrations de X et X̄ se passent pendant une courte
période à la température T1 et au paramètre d’échelle a1 . En négligeant l’expansion
pendant la période de désintégration, calculer l’excès de nombre baryonique ∆nb =
nb − n̄b engendré par les désintégrations en fonction de la densité originale nX des X,
avec nX = n̄X .
(c) Quel est le rapport baryon/photon η(a1 ) = ∆nb /nγ juste après la période de
désintégration ?
Après la période de désintégration, on suppose qu’il n’y a plus d’interactions violant le nombre baryonique si bien que l’excès est conservé :
a 3
1
∆nb (a) = ∆nb (a1 )
.
a
ÉC
E
L
O
T
Y
L
PO
(d) Si gs (T1 ) est le nombre d’états de spin relativistes à T1 , calculer la valeur actuelle
de η(a0 ) = ∆nb /nγ en supposant que l’expansion a été adiabatique après t1 .
On dit qu’une réaction viole l’invariance « C » si l’« antiréaction » où toutes
les particules sont remplacées par leurs antiparticules n’a pas le même taux que la
réaction initiale. On dit qu’une réaction viole l’invariance « P » si la réaction vue
dans un miroir n’a pas le même taux que la réaction initiale 5 . Enﬁn, une réaction
viole « CP » si le processus vu dans un miroir avec les particules remplacées par leurs
antiparticules n’a pas le même taux que la réaction initiale.
5À
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
strictement parler, l’opération P renverse toutes les coordonnées alors que la réﬂexion par
un miroir ne renverse que la coordonnée perpendiculaire au miroir. Cependant, la réﬂexion par un
miroir suivie d’une rotation appropriée peut renverser toutes les coordonnées. La réﬂexion par un
miroir est par conséquent équivalente à P si l’invariance par rotation est respectée.
ÉC
E
Exercices sur le chapitre 6
N
H
EC
E
U
IQ
265
Il est clair que si C n’est pas violé, le taux de X → d̄e+ doit être le même que
celui de X̄ → de− , ce qui implique que r = r̄.
(e) Le fait que CP doit être violé pour avoir r = r̄ peut se comprendre en considérant
la désintégration d’une particule classique avec un moment cinétique propre (spin).
Dessiner la réaction X → d̄e+ en face d’un miroir. On observera que les spins de
toutes les particules sont renversés sur l’image dans le miroir. Imaginons que toutes
les particules dans le miroir sont les antiparticules des particules originale. Discuter
le fait que si la réaction dans le miroir se passe avec le même taux que la réaction
originale pour toutes les combinaisons possibles des spins de la réaction originale, c’est
à dire si CP n’est pas violé, alors r = r̄ après que l’on a moyenné sur tous les spins
possibles.
(f ) Une réaction viole « CPT » si le renversement du temps d’un processus vu dans
un miroir avec les particules remplacées par leurs antiparticules n’a pas le même
taux que le processus original. Faire un croquis du processus de diﬀusion résonante
d̄e+ → X → d̄e+ placé devant un miroir. Expliquer que la réaction transformée par
CPT de− → X̄ → de− serait vue sur un ﬁlm passé à l’envers dans le miroir avec les
particules remplacées par leurs antiparticules. Les deux réactions vont avoir un pic de
résonance à une énergie dans le centre de masse égale à mX pour la première réaction
et mX̄ pour la seconde. Si l’invariance CPT est respectées, la section eﬃcace de la
première réaction doit être égale à celle de la seconde. À cause de la présence des
pics de résonance dans la dépendance en énergie des deux sections eﬃcaces, expliquer
pourquoi les masses et largeurs totales (durées de vie) de X et X̄ sont égales.
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
6.10 La section eﬃcace multipliée par la vitesse pour la réaction np → 2 H γ est
σv ∼ 7.4 × 10−20 cm3 s−1
(v c) .
(6.118)
(a) Montrer que le taux de cette réaction par nucléon est inférieur au taux d’expansion
à T ∼ 60 keV si η < 4 × 10−12 . Il s’ensuit qu’il n’y a pas de nucléosynthèse si η est
inférieure à cette valeur.
(b) Si η > 4 × 10−12 , le deutérium est en équilibre thermique avec les neutrons et
les protons. En imposant µ2 = µp + µn montrer que l’abondance du deutérium, des
protons et des neutrons est régie par l’équation de Saha :
Å
ã
2π 2π m2 T 3/2 B/T
n2
=
e
np nn
mn T mp T 2π
H
C
TE
U
Q
I
N
où B = 2.2 MeV est l’énergie de liaison du deutérium.
(c) Montrer que pour η ∼ 5 × 10−10 la grande majorité des neutrons sont libres
jusqu’à T ∼ 60 keV. (Puisque la majorité des baryons sont des protons, on peut faire
l’approximation np ∼ ηnγ .)
E
L
O
Y
L
PO
6.11 Calculer la durée de l’époque de désintégration du neutron [t(60 keV)−t(800 keV)].
Estimer l’entropie créée par ce processus irréversible. Discuter comment la « nucléo-
ÉC
E
266
E
U
IQ
Chapitre 6. L’histoire thermique de l’univers
T
Y
L
PO
N
H
EC
destruction » dans une phase de contraction d’un univers fermé diﬀèrerait de la
nucléosynthèse en phase d’expansion renversée par rapport au temps.
E
L
O
6.12 Considérons la température de gel (6.87) des réactions faibles qui transforment
les neutrons en protons. La valeur de Tg dépend, au travers du taux d’expansion, du
nombre d’états de spin relativistes et, par conséquent, du nombre Nν d’espèces de
neutrinos (ou de n’importe quelle espèce de particule légère à l’équilibre thermique).
Le nombre de neutrons disponibles pour la production d’hélium dépend donc de Nν .
Pour simpliﬁer les choses, nous supposons que les abondances observées d’éléments
légers sont en accord avec les abondances calculées pour η ∼ 5 × 10−10 et Nν = 3.
Si l’abondance n4 de 4 He est connue avec une précision de 10%, donner une limite
supérieure à Nν .
Avant la mesure de Nν = 3 au collisionneur LEP en utilisant la largeur de désintégration du Z 0 , La limite cosmologique sur Nν était beaucoup plus forte que les
limites expérimentales. Il faut souligner que la mesure du LEP est sensible aux particules neutres interagissant faiblement qui se couplent au Z 0 et qui ont des masses
< MZ . De l’autre côté, la limite cosmologique s’applique à n’importe quelle espèce de
particule légère en équilibre thermique à T ∼ MeV.
ÉC
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
E
T
Y
L
PO
N
H
EC
E
U
IQ
E
L
7
CO
ÉChapitre
La formation des structures
N
H
EC
E
U
IQ
L’idée de base de la formation des structures est assez simple. Dans un passé
pas trop distant (â < (ΩM /ΩΛ )1/3 ∼ 0.75), l’univers a été dominé par la matière
avec une densité moyenne presque critique ρ̄ ∼ 3H 2 /8πG. Dans ces conditions, une
région où se produit une petite ﬂuctuation de densité va se retrouver avec une densité
surcritique et, en suivant l’argument newtonien du chapitre 1, une énergie totale
négative. Comme l’illustre la ﬁgure 7.1, on s’attend à ce que les particules dans la
région sur-dense se comportent comme si elles étaient dans un mini-univers fermé.
Elle vont d’abord participer à l’expansion universlle mais, à cause de l’excès de masse,
elles vont décélérer par rapport au taux d’expansion universelle. La région sur-dense
va atteindre une extension maximum, après laquelle les particules vont retomber sur
elles-mêmes pour former une structure liée gravitationnellement.
Bien que cela soit essentiellement ce qui se passe pendant l’époque de la domination de la matière, l’évolution des inhomogénéités de densités est plus complexe
pendant l’époque du rayonnement. À cette époque, la pression élevée p = ρ/3, fait
que les inhomogénéités du plasma photon-particules chargées oscillent comme des
ondes acoustiques si la taille caractéristique de l’inhomogénéité est plus petite que la
distance de Hubble à cette époque. De même, les particules relativistes qui interagissent faiblement (par exemple les neutrinos) peuvent tout simplement s’échapper des
régions sur-denses de taille < dH par « écoulement libre ».
À cause de la possibilité d’eﬀets comme les ondes acoustiques et l’écoulement
libre des particules, des sur-densités d’une étendue plus petite que dH (t) peuvent
être dispersées pendant l’époque du rayonnement. Il est donc important de comparer
la taille d’une perturbation de densité avec dH (t). Tant que la région sur-dense est
toujours en expansion, sa taille est en gros proportionnelle à a(t). Cela doit être
comparé à dH ∝ a2 (∝ a3/2 ) pendant les époques de rayonnement et de matière.
Par conséquent, une région sur-dense commence par être plus grande que distance
de Hubble, puis « entre » dans le rayon de Hubble à un temps que nous appelons
« tentrée ». Nous verrons que les régions qui aujourd’hui ont une taille de < 10h−1 Mpc
sont entrées dans le rayon de Hubble pendant l’époque du rayonnement. Les ondes
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
Y
L
PO
267
H
C
TE
U
Q
I
N
E
268
E
U
IQ
Chapitre 7. La formation des structures
T
Y
L
PO
N
H
EC
acoustiques engendrées ont alors inhibé pour un temps la croissance du contraste
moyen de densité sur des échelles < 10h−1 Mpc.
Une fois que l’époque de matière a commencé, la pression est tombée à zéro et
les inhomogénéités ont pu croître à toutes les échelles si la matière est composée
principalement de particules à interaction faibles (matière noire froide). On verra que
le constraste de densité a grandi linéairement avec le paramètre d’échelle ∆ρ/ρ ∝ a(t).
Une région sur-dense atteint son extension maximale lorsque ∆ρ/ρ est de l’ordre de 1,
puis elle se contracte. Les galaxies formées vers â ∼ 1/5 existaient donc à âeq ∼ 10−4
comme des régions sur-denses de ∆ρ/ρ ∼ 5 × 10−4 .
L’essentiel de la théorie de la formation des structures s’intéresse non pas à la
formation ﬁnale de structures liées mais au problème plus simple de l’évolution des
ﬂuctuations de densité dans leurs premières étapes, lorsque le contraste de densité est
encore faible. La grandeur essentielle dans ce chapitre, sera la ﬂuctuation de la masse
MRâ contenue dans une sphère de rayon Râ :
ÉC
E
L
O
2
− MRâ 2 ,
(∆MRâ )2 = MRâ
N
H
EC
E
U
IQ
(7.1)
où les signiﬁent que l’on moyenne sur la position des diverses sphères. Si les
ﬂuctuations de densité sont gaussiennes, comme on s’y attend pour les ﬂuctuations
primordiales engendrées par l’inﬂation, les ﬂuctuations sont entièrement caractérisées
par la variance ∆MRâ . Dans ce cas, on s’attend à ce que les ﬂuctuations restent
gaussiennes tant qu’elles sont faibles, ∆M/M 1.
Utilisant une notation qui sera rendue plus claire à la section 2, nous utiliserons
le terme ∆k pour les ﬂuctuations relatives de MRâ :
ÉC
E
L
O
T
Y
L
PO
∆MRâ
∼ ∆k (a)
MRâ k ∼ 1/R .
(7.2)
On parle de ﬂuctuations de densité « d’échelle » R, c’est-à-dire la taille des sphères
aujourd’hui. On choisit un rayon de la sphère proportionnel à a(t) puisque la matière
dans les sphères participe à l’expansion tant que le contraste de densité est faible.
L’univers apparaît grumeleux à petite échelle et homogène à grande échelle. On
s’attend donc à ce que ∆k soit une fonction croissante de k. Cela est conﬁrmé par
les ﬂuctuations du nombre volumique de galaxies montré sur la ﬁgure 7.4. Le spectre
croît avec k puis voit sa pente décroître lentement autour de k −1 ∼ 10h−1 Mpc.
Ce changement de pente provient des oscillations acoustiques à l’échelle mentionnée
ci-dessus.
Aux échelles les plus grandes, les mesures de l’anisotropie du CBR (section 9)
indiquent que ∆k ∝ R−2 pour R 20 Mpc.
Comme nous l’avons déjà souligné, l’évolution de ∆k est déterminée par la gravitation et des eﬀets de microphysique, comme les oscillations acoustiques et l’écoulement
libre de particules. Pour la matière noire froide, la gravité domine et les ﬂuctuations
de matière noire froide croissent avec le temps pendant l’époque de matière comme
∆k (a) ∝ a(t) tant que ∆k (a) 1. La ﬁgure 7.2 illustre cette évolution.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
269
E
U
IQ
ρ=ρc
ρ>ρc
ÉC
E
L
O
T
Y
L
PO
N
H
EC
Fig. 7.1: Formation des structures dans un univers avec ΩM = ΩT ∼ 1. Dans un tel univers,
une région sur-dense (ρ > ρc ) peut évoluer comme un mini-univers fermé. La région va se
dilater jusqu’à atteindre un rayon maximum puis se détacher de l’expansion universelle en
se contractant pour former un objet gravitationnellement lié alors que le reste de l’univers
continue son expansion. Dans un univers avec ΩM signiﬁcativement plus petit que 1, une
petite sur-densité ne sera pas suﬃsante pour rendre la région sur-critique et la région sera en
expansion éternelle. Dans un univers avec ΩM signiﬁcativement plus grand que 1, les régions
avec une petite sur-densité n’ont pas le temps de former des structures avant que l’univers
s’eﬀondre comme un tout.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
270
ÉC
E
U
IQ
Chapitre 7. La formation des structures
E
L
O
T
Y
L
PO
N
H
EC
ρ
3a
2a
a
x/a(t)
ρ (a)
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
Fig. 7.2: Évolution des inhomogénéités de densité dans un univers dominé par la matière
noire froide. La ﬁgure montre une perturbation de densité à peu près sinusoïdale à trois
époques, a, 2a, et 3a. On suppose que la perturbation est petite (∆ρ/ρ 1) de façon que les
tailles des régions sur-denses et sous-denses soient à peu près proportionnelles à a(t). Les
régions sur-denses subissent une expansion de taux légèrement inférieur à celui des régions
sous-denses. Il en résulte que le contraste de densité croît linéairement avec le paramètre
d’échelle. Dans un univers qui n’est pas dominé par la matière noire froide, divers eﬀets de
microphysique peuvent inhiber la formation des structures. Pendant l’époque du rayonnement,
les inhomogénéités d’extension < dH dans le plasma baryon/photon oscillent comme des
ondes acoustiques. Les particules relativistes à interactions faibles (neutrinos) s’échappent
des régions sur-denses d’extension < dH par « écoulement libre ».
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
T
Y
L
PO
N
H
EC
E
U
IQ
271
En dépit de la simplicité de ce scénario, il n’existe pas de modèle universellement
accepté de la formation des structures en raison de notre ignorance sur trois points
essentiels :
E
L
O
– Les conditions « initiales ». Pour expliquer le spectre actuel des ﬂuctuations de
densité, il est nécessaire de spéciﬁer à un certain instant de l’univers primordial
l’amplitude et la nature des inhomogénéités en fonction de l’échelle.
Les seules indications observationnelles que l’on ait sur ce sujet proviennent
du spectre des anisotropies du CBR. Celles-ci peuvent être interprétées comme
étant dues aux inhomogénéités de densité à trec sur des échelles λ qui sont
maintenant dans la gamme 0.001H0−1 < λ < H0−1 . Pour ce qui concerne la
nature des ﬂuctuations, celles-ci peuvent être des ﬂuctuations « adiabatiques »
de la densité d’énergie totale, ou bien des ﬂuctuations « d’iso-courbure » de la
composition chimique, par exemple le rapport baryon/photon η :
ÉC
∆ρ/ρ = 0
∆ρ/ρ = 0
∆η/η = 0
∆η/η = 0
E
U
IQ
ﬂuctuations adiabatiques ,
(7.3)
ﬂuctuations d iso − courbure .
(7.4)
T
Y
L
PO
N
H
EC
les ﬂuctuations d’iso-courbure peuvent, bien, évidemment, impliquer d’autres
rapports comme nwimp /nγ . Une ﬂuctuation quelconque sera en général une
combinaison de ﬂuctuations adiabatiques et de tous types de ﬂuctuations d’isocoubure.
ÉC
E
L
O
– Les valeurs des paramètres cosmologiques. ΩM détermine le début de l’époque
de matière lorsque la formation des structures peut se dérouler sans être inhibée
par les oscillations acoustiques ou par l’écoulement libre de particules : âeq =
1.68Ωγ /ΩM . Si ΩM < 1, cela détermine également la ﬁn de cette époque, âcΛ ∼
ΩM /(1 − ΩM ) si ΩΛ ∼ 0 ou âcΛ ∼ (ΩM /ΩΛ )1/3 si ΩT ∼ 1.
– La nature de la matière noire. Les oscillations acoustiques cessent d’interférer
avec la formation des structures à âeq ∼ 10−4 seulement si la matière noire
est composée d’objets lourds interagissant faiblement (matière noire froide). Les
baryons sont fortement couplés au gaz relativiste de photons dont la pression les
empêche de s’eﬀondrer gravitationnellement jusqu’au découplage à ârec ∼ 10−3 .
En outre, les ﬂuctuations adiabatiques de baryons sur les échelles galactiques
sont amorties par l’entraînement de la matière par les photons (« amortissement
de Silk ») à la recombinaison.
H
C
TE
U
Q
I
N
En l’absence d’éléments observationnels sûrs sur ces trois points, un modèle de la
formation des structures doit être paramétrisé par une distribution d’inhomogénéités
initiales, par les valeurs des paramètres cosmologiques, et par la nature de la matière
noire. Comme nous allons le voir, un modèle peu être utilisé pour prédire diverses
quantités observables : le spectre actuel des inhomogénéités de densités, le spectre des
vitesses particulières causées par des taux d’expansion diﬀérentiels, et le spectre des
anisotropies du CBR.
ÉC
E
L
O
Y
L
PO
E
272
E
U
IQ
Chapitre 7. La formation des structures
T
Y
L
PO
N
H
EC
Presque toutes les observations sont compatibles avec un modèle « standard »
de la formation des structures. Ce modèle utilise les valeurs actuellement en vogue
des paramètres de densité, ΩM ∼ 0.3 et ΩΛ ∼ 0.7. Pour le spectre primordial, le
modèle utilise des « ﬂuctuations adiabatiques invariantes d’échelle ». La raison de ce
choix est en partie d’origine théorique (l’inﬂation mène très naturellement à de telles
ﬂuctuations) et en partie observationnelle (les anisotropies du CBR s’expliquent très
naturellement par un spectre de ce type) Enﬁn, pour éviter l’amortissement de Silk
et d’autres problèmes, les modèles avec des ﬂuctuations adiabatiques doivent recourir
à de la matière noire froide (Sect. 7).
La théorie de la formation des structures est nécessairement un sujet beaucoup
plus diﬃcile que la cosmologie d’un univers homogène. Nous avons été menés à la
métrique de Robertson–Walker et à l’équation de Friedmann parce que les symétries
de l’isotropie et l’homogénéité ne laissaient pas grand choix. Établir un système de
coordonnées et les équations d’Einstein pour un univers inhomogène est une tâche
diﬃcile techniquement. Le concept même de contraste de densité est mal-déﬁni car
il implique de comparer les densités en des points diﬀérents au même moment. Cela
dépend donc de notre choix d’horloges et de la procédure de synchronization. Ce point
est particulièrement diﬃcile lorsque l’on traite d’échelles plus grandes que dH puisque
des horloges ne peuvent même par être comparées en échangeant des photons.
À cause de ces diﬃcultés techniques, nous allons seulement présenter la théorie de
la formation des structures sur des exemples simpliﬁés qui vont illustrer les résultats
généraux. Les lecteurs intéressés devront se reporter à des textes plus avancés [13, 14,
15, 16, 17, 18, 19] pour les détails. Nous commencerons, en section 1 par étudier un
univers isotrope qui est homogène sauf dans une région sur-dense proche de l’origine.
Le problème sera traité de façon relativiste mais sera limité au cas simple d’une
pression nulle et il est donc plus directement applicable à un univers dominé par de
la matière noire froide. Le modèle va nous permettre de tirer quelques conclusions
importantes sur la croissance des inhomogénéités en régime linéaire et sur la nature
des objets formés après l’eﬀondrement gravitationnel.
Dans la section 2, nous discuterons plus précisément le spectre des ﬂuctuations de
densité ∆k . L’information sur cette fonction provient des ﬂuctuations dans le comptage des galaxies et du nombre volumique d’amas de galaxies. Nous verrons comment
les observations ce comprennent beaucoup plus facilement si ΩM est signiﬁcativement
inférieur à 1, ΩM ∼ 0.4.
L’évolution de ∆k aura été anticipée dans certains résultats de la section 1 mais
elle sera illustrée plus à fond par un traitement newtonien des ﬂuctuations de densité
dans la section 3. Ce traitement nous permettra de déterminer dans quelles conditions
une ﬂuctuation de densité se propage comme une onde acoustique plutôt que comme
un eﬀondrement gravitationnel.
Le moment critique de l’« entrée dans le rayon de Hubble » sera calculé en fonction
de l’échelle dans la section 4. La distinction entre les échelles qui entrent en jeu avant et
après qu’il y ait égalité matière-rayonnement sera discutée et soulignée. Nous verrons
aussi comment il a pu y avoir une « sortie du rayon de Hubble » pendant une époque
inﬂationnaire.
ÉC
E
L
O
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
E
Un modèle d’eﬀondrement sphérique
T
Y
L
PO
N
H
EC
E
U
IQ
273
Le dernier élément nécessaire pour prévoir le spectre actuel des ﬂuctuations est le
spectre primordial. Les diverses possibilités seront discutées dans la section 5. Nous
mettrons l’accent sur le spectre « invariant d’échelle » (ou de « Harrison–Zel’dovich »)
où toutes les échelles entrent dans le rayon de Hubble avec des ﬂuctuations de même
amplitude, ∆H . Nous montrerons comment les modèles inﬂationnaires engendrent
naturellement un spectre de ce type.
Tous ces éléments seront assemblés dans la section 6 pour donner le spectre prédit
par les modèles de matière noire froide et un spectre invariant d’échelle de ﬂuctuations
primordiales adiabatiques. Nous comparerons les résultats avec les observations.
L’utilisation de la matière noire froide dans la formation des structures appelle
quelques justiﬁcations puisqu’aucune particule correspondante n’a été directement
observée et identiﬁée. Avec cette idée en tête, nous discuterons dans la section 7 les
problèmes qui se posent avec des modèles qui font usage de neutrinos massifs légers
(« matière noire chaude ») ou simplement de la matière noire baryonique.
Dans la section 8 nous traiterons le problème de la propagation des photons dans
un univers inhomogène. Cela nous permettra, dans la section 9, de discuter les anisotropies du CBR prévues par les modèles de matière noire froide. Comme nous le
verrons, la mesure de ces anisotropies devraient permettre la détermination des paramètres cosmologiques avec une précision sans précédent.
ÉC
E
L
O
N
H
EC
1
E
U
IQ
T
Y
L
O
Un modèle d’eﬀondrement
sphérique
P
E
L
ÉCO
Dans le scénation standard de la matière noire froide, la formation d’un objet gravitationnellement lié à partir d’une région avec une petite sur-densité est un processus
en trois étapes :
– L’expansion de la région jusqu’à son maximum.
– La contraction de la région jusqu’à la virialisation des particules et la formation
d’une structure liée. Le processus de virialisation [141] est appelé « relaxation
violente ». Il est non-dissipatif en ce sens que l’énergie newtonienne de la région
est approximativement conservée pendant l’eﬀondrement1 .
– La contraction « dissipative » de la composante baryonique par rayonnement
de photons. D’autres processus nonlinéaires comme la fusion de soustructures
sont importants dans cette étape.
On pense généralement que les amas de galaxies et les halos galactiques sont
avant tout le résultat des deux premières étapes. La troisième est essentielle dans la
formation d’objets baryoniques comme les disques galactiques et les étoiles.
Dans cette section nous allons suivre les deux premières étapes pour une région
sphérique avec une sur-densité initiale. À cause de la symétrie sphérique, il est plausible de penser que la dynamique de la région sur-dense sera indépendante de la
1 On
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
notera que cet eﬀet semble au premier abord « paradoxal » puisqu’il est impossible dans
un système à deux corps, où l’énergie de liaison doit être évacuée par un processus radiatif. Il a une
certaine similitude avec la formation du cœur des supernovae de type II où le rebond de la matière
après l’eﬀondrement gravitationnel laisse derrière lui un noyau lié, l’étoile à neutrons.
ÉC
E
274
E
U
IQ
Chapitre 7. La formation des structures
T
Y
L
PO
N
H
EC
dynamique universelle. En relativité générale, cette indépendence est, en eﬀet, garantie par le théorème de Birkhoﬀ, l’analogue du théorème de Gauss. L’analyse que
nous présentons ici va conﬁrmer ce théorème en montrant que la région sur-dense est
eﬀectivement régie par sa propre équation de Friedmann. Si la sur-densité est suﬃsamment importante, son équation de Friedmann sera celle d’un univers fermé. Dans
un univers critique, une sur-densité initiale inﬁnitésimale suﬃt à fermer la région.
Les particules dans la région sur-dense vont ensuite se détacher de l’expansion et se
contracter, conﬁrmant ainsi notre intuition newtonienne.
Il faut souligner qu’en réalité, le processus de formation des structures n’est pas
à symétrie sphérique. Des simulations à N-corps (N grand) [142] montrent que l’effondrement non-sphérique donne une distribution « ﬁlamenteuse » de matière où les
amas de galaxies se forment à l’intersection des ﬁlaments. Les structures vues dans les
observations de redshifts (Fig. 2.14) sont, en partie, une réﬂexion de cette structure
de densité. Le modèle d’eﬀondrement sphérique est, cependant, utile pour développer
une intuition de la formation des structures et pour estimer les ordres de grandeur.
ÉC
E
L
O
1.1
La métrique
T
Y
L
PO
N
H
EC
E
U
IQ
Considérons un univers de pression nulle avec une densité variant radialement :
ÉC
E
L
O
ρ = ρ(r, t)
p = 0.
(7.5)
Pour le système de coordonnées, l’isotropie nous permet d’utiliser les coordonnées
angulaires (θ, φ) comme dans un univers homogène. Si l’inhomogénéité de densité est
faible, on peut aussi utiliser des horloges comobiles avec des coordonnées spatiales ﬁxes
pour mesurer la coordonnée temporelle. De telles horloges ne sont plus très utiles dès
que se forment des structure liées puisque les trajectoires des horloges vont se croiser,
ce qui rend les coordonnées extrêmement compliquées.
Avec une coordonnée radiale r arbitraire, l’isotropie et l’utilisation d’horloges comobiles implique que la métrique prend la forme suivante :
dτ 2 = dt2 − A(r, t) dr2 − B(r, t) (dθ2 + sin2 θ dφ2 ) .
(7.6)
U
Q
I
N
À partir de cette métrique, l’équation d’Einstein peut être écrite [161] et nous invitons
le lecteur à le faire dans l’exercice 7.1. Les solutions des équations ne sont pas uniques
car nous avons encore la liberté de choix de la coordonnée radiale. Néanmoins, toutes
les solutions vont satisfaire la conservation de l’énergie :
E
L
O
Y
L
PO
√
∂ρ AB
= 0.
∂t
H
C
TE
(7.7)
Cette relation garantit
du nombre de particules dans un volume co√
√ la√conservation
mobile ﬁxé, dV = Adr Bdθ B sin θdφ.
ÉC
E
Un modèle d’eﬀondrement sphérique
T
Y
L
PO
N
H
EC
E
U
IQ
275
Il est possible (exercice 7.1) de choisir la coordonnée radiale r de façon que la
métrique prenne une forme très semblable à celle de Robertson–Walker :
ñ
ô
Å
ã
r ∂b 2
dr2
2
2
2
2
2
2
2
1+
− r (dθ + sin θ dφ ) .
(7.8)
dτ = dt − b(r, t)
1 − κ(r)r2
b ∂r
ÉC
E
L
O
Avec cette métrique, les équations d’Einstein sont telles que la « fonction d’échelle »
b(r, t) satisfait une équation du même type que l’équation de Friedmann, que nous
nommons dans la suite « équation Friedmannienne » :
Ç å2
Å
ã
r ∂b
ḃ
κ(r)
8πG
ρ
1
+
,
+
=
b
b2
3
b ∂r
et la conservation de l’énergie (7.7) prend la forme
ρ(r, t) =
constante
.
b3 (1 + (r/b)(∂b/∂r))
T
Y
L
PO
N
H
EC
(7.9)
E
U
IQ
(7.10)
De même que le paramètre de courbure k de la métrique de Robertson–Walker, la
« fonction de courbure » κ(r) est déterminée par les conditions à un instant arbitraire
que nous appellerons t1 :
ÉC
1.2
E
L
O
κ(r)
= −
b(r, t1 )2
Ç å2
Å
ã
ḃ
8πG
r ∂b
ρ(r, t1 ) 1 +
+
.
b t
3
b ∂r t1
(7.11)
1
Expansion et eﬀondrement
Les équations (7.9) et (7.10) vont nous permettre de comprendre l’évolution d’une
petite région sur-dense r < rc au « centre » d’un univers par ailleurs homogène :
|δ1 | 1
ρ(r < rc , t1 ) = ρ̄(t1 )(1 + δ1 )
ρ(r > rc , t1 ) = ρ̄(t1 ) .
(7.12)
(7.13)
U
Q
I
N
Dans la section 8, nous trouverons une solution de l’équation Friedmannienne (7.9)
avec ces conditions initiales. Ici, nous nous concentrons sur les conditions en r = 0 et
en r rc . Cela sera suﬃsant pour illustrer les aspects essentiels du problème.
Il est plausible que (r/b)∂b/∂r = 0 en r = 0 et pour r rc , et cette conjecture
sera conﬁrmée dans la section 8. Dans ce cas, l’équation Friedmannienne est simplement une équation de Friedmann pour chaque point. Nous pouvons donc déﬁnir le
paramètre d’échelle « central » ac (t) et le paramètre d’échelle moyen a(t) :
ÉC
E
L
O
ac (t) ≡ b(r = 0, t)
Y
L
PO
H
C
TE
a(t) ≡ b(r rc , t) .
(7.14)
E
276
E
U
IQ
Chapitre 7. La formation des structures
N
H
EC
Pour r rc , (7.9) est simplement :
Å ã2
ȧ
= H12 (Ω1 ã−3 + (1 − Ω1 )ã−2 ) ,
a
E
L
O
T
Y
L
PO
(7.15)
où, comme dans le chapitre 4, nous avons utilisé (7.11) pour mettre l’équation de
Friedmann dans une forme qui utilise le taux d’expansion et les paramètres de densité
à un temps donné t1 :
Å ã
a(t)
ȧ
ρ̄(t1 )
ã(t) =
.
(7.16)
H1 =
Ω1 =
a t1
3H12 /8πG
a(t1 )
ÉC
De même, pour r = 0, (7.9) est l’équation de Friedmann pour ac :
Å ã2
ȧc
2
−2
= Hc1
(Ωc1 ã−3
c + (1 − Ωc1 )ãc ) ,
ac
où
Å
Hc1 =
ȧc
ac
ã
Ωc1 =
t1
N
H
EC
ρ(r = 0, t1 )
2 /8πG
3Hc1
T
Y
L
PO
ãc (t) =
E
U
IQ
(7.17)
ac (t)
.
ac (t1 )
(7.18)
Les structures actuelles ont été formées lorsque l’univers était dominé par la matière avec une densité presque critique. Nous prenons donc Ω1 = 1 dans quel cas la
petite sur-densité à r = 0 peut rendre la région centrale sur-critique avec Ωc1 > 1.
Comme l’illustre la ﬁgure 7.3, le paramètre d’échelle central ãc va alors augmenter
jusqu’à tmax où il atteint une valeur maximum, Ωc1 /(Ωc1 − 1), quand ȧc = 0, après
quoi la région centrale se met à se contracter. Dans le chapitre 5 nous avons calculé le
temps tmax (5.80) nécessaire pour atteindre l’expansion maximum. Pour Ωc1 − 1 1
le temps est donné par
ÉC
E
L
O
tmax = t1
3π
4(Ωc1 − 1)3/2
ãc (tmax ) ∼
1
.
Ωc1 − 1
(7.19)
Si la densité moyenne est critique, Ω1 = 1, le paramètre d’échelle moyen a(t) est
proportionnel à t2/3 . Il s’ensuit que lorsque la région sur-dense est à son expansion
maximale, a(t) prend la valeur
Å
ã
Å ã2/3
tmax 2/3
1
3π
ã(tmax ) =
=
.
(7.20)
t1
Ωc1 − 1 4
Le contraste de densité à tmax est
ρ(r = 0, tmax )
∼
ρ̄(tmax )
E
L
O
Å
ã3
H
C
TE
Å
Y
L
PO
a(tmax )
ac (tmax )
=
3π
4
ã2
= 5.55 .
U
Q
I
N
(7.21)
Après tmax , la matière dans la région centrale se met à se contracter avec l’apparition d’un « objet » à ∼ 2tmax . (Le processus de virialisation eﬀective prend un peu
plus de temps.)
ÉC
E
Un modèle d’eﬀondrement sphérique
N
H
EC
E
U
IQ
277
Le temps ∼ 2tmax nécessaire pour former une structure qui commence à t1 est
déterminé par Ωc1 − 1 (au travers de (7.19)). Ωc1 − 1 est déterminé par le contraste de
densité δ1 à t1 et par la diﬀérences des taux d’expansion (Hc1 − H1 )/H1 = ∆H1 /H1
à t1 :
ÉC
E
L
O
T
Y
L
PO
Ωc1 − 1 =
=
ρ(r = 0, t1 )
2 /8πG − 1
3Hc1
ρ̄(1 + δ1 )
2∆H1
− 1 ∼ δ1 −
.
(3H12 /8πG)(1 + 2∆H1 /H1 )
H1
(7.22)
A priori, ∆H1 /H1 est indépendant de δ1 mais on peut s’attendre à ce qu’il soit
négatif à cause de la décélération relative de la région sur-dense. De fait, nous verrons
ci-dessous qu’un état stationnaire est rapidement atteint avec ∆H/H ∼ −(1/3)δ. En
appliquant cela à t1 , on trouve
N
H
EC
Ωc1 − 1 = ∼ (5/3) δ1 .
E
U
IQ
(7.23)
En substituant cela dans (7.20), on voit que le temps nécessaire pour former un objet
en commençant avec une sur-densité de δ1 correspond à une expansion moyenne de
l’ordre de 1/δ1 :
ÉC
E
L
O
T
Y
L
PO
a(tmax )
1
∼
.
a(t1 )
δ1
(7.24)
Par exemple, les galaxies qui se sont formées à â ∼ 1/5 devaient exister à teq (âeq ∼
10−4 ) comme des régions d’une sur-densité de l’ordre de δ ∼ 5 × 10−4 .
Certaines caractéristiques des objets formés par l’eﬀondrement non-dissipatif peuvent s’évaluer facilement parce que peu d’énergie s’échappe dans la région environnante pendant l’eﬀondrement. En suivant le raisonnement de la section 2.2, l’énergie
newtonienne E1 à t1 d’une particule typique dans la région centrale est
2
(1 − Ωc1 ) ,
E1 = T1 + U1 ∼ (1/2)mrc2 a2c1 Hc1
(7.25)
U
Q
I
N
où T1 et U1 sont l’énergie cinétique et l’énergie potentielle gravitationnelle. Après
l’eﬀondrement, on peut supposer que les particules sont virialisées et que (la valeur
absolue de) l’énergie potentielle par particule, U0 , est double de l’énergie cinétique
par particule, T0 :
U0 = −2T0
Y
L
PO
H
C
TE
⇒ E0 = −T0 ∼ −(1/2)m(∆v)2 ,
(7.26)
où ∆v est la dispersion en vitesse de la structure virialisée. En posant E0 = E1 , on
peut estimer ∆v :
ÉC
E
L
O
2
(1 − Ωc1 ) .
(∆v)2 ∼ rc2 a2c1 Hc1
(7.27)
E
278
ÉC
E
U
IQ
Chapitre 7. La formation des structures
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
T
Y
L
PO
N
H
EC
E
U
IQ
Fig. 7.3: Le paramètre d’échelle moyen a(t) et le paramètre d’échelle central ac (t) en fonction
du temps. Les conditions initiales choisies sont δ1 = 10−3 et ∆H1 /H1 = −δ1 /3. L’univers
est dominé par la matière avec une densité critique si bien que log(a/a1 ) = (2/3) log(t/t1 ).
On voit que ac atteint sa valeur maximum après que a se soit accru d’un facteur ∼ 1/δ1 .
Après l’expansion maximale, la région centrale se contracte d’un facteur ∼ 2 pour former
une structure virialisée.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Un modèle d’eﬀondrement sphérique
T
Y
L
PO
N
H
EC
E
U
IQ
279
Pour donner un sens à cette formule, il est utile de prendre pour t1 l’instant où le
−1
rayon de la région centrale est égal à la distance de Hubble, a1 rc = Hc1
∼ H1−1 . Dans
ce cas, on trouve simplement
ÉC
E
L
O
(∆v)2 = (1 − Ωc1 ) ∼ δ(tentrée ) ,
(7.28)
c’est-à-dire que le carré de la dispersion en vitesse est de l’ordre du contraste de densité
au moment où l’échelle de l’objet entre dans le rayon de Hubble. Par le théorème du
viriel, c’est également l’ordre de grandeur de la profondeur Φ du potentiel newtonien
de la structure virialisée :
Φ = (1 − Ωc1 ) ∼ δ(tentrée ) .
(7.29)
Ces faits très remarquables seront discutés plus avant dans la section 5.
Une autre façon d’interpréter (7.27) est de noter que rc a0 est le rayon que la région
aurait si elle ne s’était pas eﬀondrée :
Å
rc a0 ∼
M
4π ρ̄(a0 )/3
N
H
EC
ã1/3
,
T
Y
L
PO
E
U
IQ
(7.30)
où M est la masse de l’objet. En substituant cela dans (7.27) on trouve
ÉC
E
L
O
(∆v)2 ∼
Ç
rc a0
H0−1
å2
a2c1
a20
Å
H1
H0
ã2 Å
∆ρ
ρ
ã
.
(7.31)
t1
Les plus grands amas de galaxies ont M ∼ 1015 h−1 M ce qui implique rc a0 ∼
15h−1 Mpc. Leur dispersion en vitesse est typiquement ∼ 3 × 10−3 c. L’équation (7.27)
et l’équation de Friedmann impliquent un contraste de densité à teq , sur une échelle
de 15h−1Mpc, de
ï
∆ρ
ρ
ò
∼ (3 × 10−3 )2
teq
Å
3000 h−1
15h−1
ã2
âeq ∼ 10−4 ,
(7.32)
où nous avons pris ΩM ∼ 1 comme première approximation.
La dernière quantité que nous allons estimer est la densité des structures ainsi
formées. À tmax , l’énergie cinétique est nulle et E(tmax ) = U (tmax ). Puisque le potentiel gravitationnel est proportionnel à l’inverse de la taille de la structure, il s’ensuit
qu’entre tmax et la virialisation, le rayon de l’objet se contracte d’un facteur deux :
U0 = 2E = 2U (tmax ). Pendant ce temps, a(t) est multiplié par un facteur ∼ 22/3 . Le
contraste de densité au moment de la virialisation est donc en gros
Y
L
PO
H
C
TE
ρ(r = 0, 2tmax)
∼ 5.55 × 23 × 22 = 177 .
ρ̄(2tmax )
E
L
O
U
Q
I
N
(7.33)
Après cela, le contraste de densité croît comme a3 puisque l’objet est stationnaire et
que l’univers se dilue comme a−3 .
ÉC
E
280
1.3
E
U
IQ
Chapitre 7. La formation des structures
Le régime linéaire
T
Y
L
PO
N
H
EC
la cosmologie s’intéresse avant tout à la croissance du contraste de densité quand il
est toujours faible, c’est-à-dire dans le régime linéaire. Nous pouvons devancer certains
résultats généraux en utilisant notre modèle d’eﬀondrement sphérique. Dans ce modèle
avec ΩM = 1, la région sur-dense se détache de l’expansion universelle lorsque le
contraste de densité est de l’ordre de un (7.21). L’équation (7.24) dit que pendant le
temps que δ s’accroît d’un facteur ∼ 1/δ, le paramètre d’échelle moyen a(t) s’accroît
également d’un facteur ∼ 1/δ. Cela suggère que tant que le contraste de densité δ est
faible, il croît linéairement avec a(t) :
ÉC
E
L
O
δ ∝ a(t)
ΩM (t) = 1 ,
ȧ
δ̇
=
δ
a
ΩM (t) = 1 .
ou, de façon équivalente
N
H
EC
(7.34)
E
U
IQ
(7.35)
Cette hypothèse sera conﬁrmée dans l’exercice 7.2.
Dans le cas d’un univers presque vide, ΩM ∼ 0, le contraste de densité ne croît
pas car à la fois la région « sur-dense » et l’univers comme un tout sont en expansion
libre avec a, ac ∝ t. À l’opposé de (7.35) on a
ÉC
E
L
O
T
Y
L
PO
δ̇
= 0
δ
ΩM (t) = 0 .
(7.36)
ce résultat sera aussi conﬁrmé dans l’exercice 7.2.
Il se trouve qu’une interpolation précise entre les deux cas pour ΩΛ = 0 est
ȧ
δ̇
∼ Ω0.6
M (t)
δ
a
ΩM ∼ ΩT < 1 .
(7.37)
Les inhomogénéités de densité engendrent des vitesses particulières à cause des
inhomogénéités du taux d’expansion. Dans le modèle d’eﬀondrement sphérique, le
taux d’expansion diﬀérentiel peut être calculé (exercice 7.2) en comparant les deux
équations de Friedmann, (7.15) et (7.17). On peut le trouver encore plus vite en
remarquant que, puisque les densités sont proportionnelles à l’inverse du cube du
paramètre d’échelle, le contraste de densité bien après t1 est
Å ã3
a
δ(t) ∼
− 1.
(7.38)
ac
Y
L
PO
H
C
TE
U
Q
I
N
En dérivant par rapport au temps et en utilisant δ̇/δ = ȧ/a on trouve
ÉC
E
L
O
ȧ
a˙c
∼ (1 − δ/3)
ac
a
ΩM (t) = 1 .
(7.39)
E
Un modèle d’eﬀondrement sphérique
T
Y
L
PO
N
H
EC
E
U
IQ
281
Comme on s’y attend, le taux d’expansion de la région sur-dense est plus faible que le
taux d’expansion universel. Ce résultat conﬁrme que ∆H1 /H1 = −δ1 /3, un résultat
que nous avons utilisé pour trouver (7.23).
La vitesse particulière radiale d’un objet proche de l’origine est la diﬀérence entre
sa vitesse et la vitesse extrapolée à sa position en utilisant le taux d’expansion à
grande échelle.
ã
Å
ȧ
ȧc
ȧ
R = (δ/3) R
ΩM (t) = 1 ,
−
(7.40)
vp =
ac
a
a
ÉC
E
L
O
où R = ac r ∼ ar. La vitesse particulière est simplement δ/3 multiplié par la vitesse
de Hubble HR. Ce fait a une interprétation newtonienne simple comme la vitesse
2
3
2
venant d’une
√ accélération de G∆M/R = GρR (∆ρ/ρ)/R sur une durée de tH =
−1
H ∼ 1/ Gρ.
On peut songer à généraliser (7.40) en utilisant δ̇/δ = ȧ/a pour ΩM (t) = 1 :
vp
δ̇
= R.
3
C
E
T
LY
Cette équation est un cas particulier de la relation générale
O
P
E
L
ÉCO
HN
E
U
IQ
· vp = −δ̇(R,
t) ∼ −H Ω0.6 δ(R,
t) ,
∇
M
(7.41)
(7.42)
où le gradient est pris par rapport aux coordonnées dans le laboratoire. Cette relation
exprime simplement la conservation de la masse, comme on peut le voir en intégrant
sur un volume et en utilisant le théorème de Gauss.
L’équation (7.42) donne une relation entre les vitesses particulières et les contrastes
de densités qui dépend de ΩM . Si les deux premiers peuvent être mesurés, on peut
estimer ΩM . En pratique ni le contraste de densité ni les vitesses particulières ne
sont simples à mesurer si bien que cette méthode n’a pas pu être utilisée avec grande
précision, mais les recherches donnent des valeurs raisonnables des Ω [143].
Il y a deux autres faits importants suggérés par le modèle d’eﬀondrement sphérique. Le premier concerne le taux de croissance des perturbations de densité pendant l’époque du rayonnement. Si la taille de la région sur-dense est plus grande que
dH (t), il ne peut y avoir de dispersion de la sur-densité par des ondes acoustiques
ou de l’écoulement libre de particules car il n’y a pas assez de temps pour que les
signaux se propagent d’une région à l’autre. Cela suggère que les deux équations de
Friedmann, (7.15) et (7.17), pour a(t) et ac (t) vont toujours s’appliquer à l’époque du
rayonnement si la taille de la région centrale est plus grande que dH (t). En revenant à
l’argument que nous avons utilisé dans le cas de la domination par la matière, on remarque que le temps nécessaire pour qu’un univers fermé dominé par le rayonnement
atteigne son expansion maximale est donné par (5.81). Ce résultat, combiné au fait
que a ∝ t1/2 , suggère que pendant l’époque du rayonnement le contraste de densité
croît comme
ÉC
E
L
O
Y
L
PO
δ ∝ a2 .
H
C
TE
U
Q
I
N
(7.43)
E
282
E
U
IQ
Chapitre 7. La formation des structures
T
Y
L
PO
N
H
EC
C’est là le taux de croissance correct pour des perturbation super-Hubble pendant
l’époque du rayonnement dans des coordonnées comobiles.
Le deuxième fait concerne les perturbations d’iso-courbure. Avec de telles perturbations, le contraste de densité initial est nul et la seule ﬂuctuation est dans les
rapports des particules, par exemple le rapport baryon/photon. En supposant une densité critique, les deux équations de Friedmann donnent des taux d’expansion égaux
pour a(t) et ac (t). Puisqu’il peut y avoir une diﬀérence de pression entre les deux
régions (à cause de diﬀérences dans les nombres de particules), la dérivée seconde des
paramètres d’échelle vont être diﬀérentes. On pourrait donc penser que cela engendre
un contraste de densité. Cependant, les équations de Friedmann pour une densité
critique agissent de façon à réguler et maintenir le proﬁl de densité plat initial. Une
petite sur-densité augmente le taux d’expansion, ce qui, en retour, diminue la densité.
Nous pouvons conclure que des perturbations d’iso-courbure super-Hubble ne peuvent pas devenir des ﬂuctuations de densité. Une fois que la région perturbée entre
dans le rayon de Hubble, la diﬀusion de particules peut engendrer des ﬂuctuations
de densité. Par exemple, une ﬂuctuation du rapport baryon/photon deviendra une
ﬂuctuation de densité après la recombinaison lorsque les photons pourront s’échapper
librement de la région perturbée.
ÉC
2
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
Le spectre des ﬂuctuations de densité
E
L
O
La quantité fondamentale dans la théorie de la formation des structures est ∆MR /MR ,
l’écart quadratique de la dispersion de la masse contenue dans des sphères de rayon
Râ. Pour justiﬁer les notation utilisées par les cosmologistes, il nous faut faire un peu
de gymnastique de Fourier.
Les variations de densité autour d’une moyenne ρ̄ sont décrites par une fonction
t) :
δ(R,
Ä
ä
t) = ρ̄(t) 1 + δ(R,
t) .
ρ(R,
(7.44)
ÉC
sont des coordonnées « dans le laboratoire » ayant la dimension
Les composantes de R
d’une longueur.
L’univers est relativement homogène sur les grandes échelles et devient grumeleux
à de plus petites échelles. Pour décrire cette dépendance dans l’échelle, il est commode
t) en série de Fourier :
de développer δ(R,
,
t0 ) = V −1/2
δk exp(i k · R)
(7.45)
δ(R,
k
Y
L
PO
H
C
TE
U
Q
I
N
où V est le volume de la région considérée. La somme porte sur toutes les ondes dont
= 0. Cela équivaut à imposer des
la moyenne est nulle sur la région, exp(i k · R)
conditions aux limites périodiques. La réalité de ρ impose δk ∗ = δ−k .
il est plus
Bien évidemment, on ne peut mesurer la densité en un seul point R,
intéressant de considérer la masse totale MR (R) dans une sphère de rayon R centrée
ÉC
E
L
O
E
Le spectre des ﬂuctuations de densité
au point R
T
Y
L
PO
|<R
R
|R−
=
MR (R)
ÉC
E
L
O
1 + V
283
)d3 r
ρ(R
= ρ̄VR
N
H
EC
E
U
IQ
−1/2
δk W (kR) exp(i k · R)
,
(7.46)
k
où VR = 4πR3 /3 et
W (kR) = VR−1
|R|<R
3
=
(kR)2
Å
d3 r
exp(i k · R)
C
E
T
LY
∼1
kR 1
∼0
kR 1 .
O
P
E
L
ÉCO
ã
HN
sin kR
− cos kR
kR
E
U
IQ
(7.47)
On voit que la fonction W (kR) tronque eﬀectivement la somme dans (7.46) si bien
que les ondes avec λ 2R ne contribuent pas à MR (comme on s’y attend).
Pour calculer les ﬂuctuations de MR , nous avons besoin de MR2 :
î
ó2
MR (R)
= ρ̄2 VR2 [1 + 2V −1/2
δk W (kR) exp(i k · R)
k
+ V −1
k
].
δk δk W (kR) W (k R) exp(i(k + k ) · R)
k
U
Q
I
N
En prenant la moyenne sur le volume V , les termes oscillants s’annulent ce qui laisse
2
2 2
−1
2
2
MR = ρ̄ VR 1 + V
|W (kR)| |δk | .
(7.48)
k
Y
L
PO
Cette expression donne la variance de MR :
Å
∆MR
MR
ã2
ÉC
E
L
O
=
H
C
TE
MR2 − MR 2
−1
=
V
|W (kR)|2 |δk |2 .
MR 2
k
(7.49)
E
284
E
U
IQ
Chapitre 7. La formation des structures
N
H
EC
Pour VR V , on peut remplacer la somme par une intégrale :
T
Y
L
PO
Å
E
L
O
∆MR
MR
ã2
1
=
(2π)3
d3 k |W (kR)|2 |δk |2 .
(7.50)
En supposant qu’il n’y a pas de direction privilégiée, on peut prendre δk = δk et l’on
trouve
Å
ã
∆MR 2
dk
|W (kR)|2 ∆2k ,
=
(7.51)
MR
k
ÉC
où
∆k ≡
k 3/2 |δk |
√
.
2π
(7.52)
E
U
IQ
La fonction ∆2k donne la contribution par unité de ln k aux ﬂuctuations de masse.
C’est donc une mesure des ﬂuctuations de densité sur l’échelle2 k −1 . Une fonction
souvent utilisée, qui lui est reliée, est le « spectre de puissance » P (k) ≡ ∆2k /k 3 .
La fonction W (kR) coupe l’intégration (7.51) pour k > 1/R. On voit que ∆k
est une fonction croissante de k et l’intégrale est en général dominée par la région
k ∼ 1/R. Une bonne approximation pour R ∼ 8h−1 Mpc est [149]
ÉC
E
L
O
T
Y
L
PO
∆MR
∼ ∆k
MR
N
H
EC
k ∼ 1.38/R .
(7.53)
L’équation (7.52) et son approximation (7.53) rendent plus précise notre déﬁnition
originale très imprécise (7.2).
La façon la plus simple d’estimer ∆k consiste à compter les galaxies et à supposer
que la ﬂuctuation dans le nombre de galaxies comptées, ∆n, est reliée aux ﬂuctuations
de densité de masse :
∆n
∆ρ
= b
,
n
ρ
(7.54)
où b est le paramètre de « bais ». Ce paramètre peut, a priori, être une fonction compliquée de l’échelle et de l’environnement. C’est par conséquent la diﬃculté d’estimer
b qui limite l’utilisation du comptage des galaxies pour estimer ∆k .
La ﬁgure 7.4 montre une compilation d’estimations de ∆k reposant sur des comptages de galaxies et d’amas de galaxies. Pour les galaxies, on voit que ∆k est de l’ordre
de 1 pour R ∼ 8h−1 Mpc et tombe à ∼ 0.1 pour R ∼ 30h−1 Mpc. Les grands relevés
de redshift en cours [144] devraient étendre ces mesures à des échelles plus grandes
2 En
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
fait, ∆k peut être directement relié à la diﬀérence entre la densité moyenne dans des sphères
de rayon R et la densité moyenne dans dans le voisinage immédiat de ces sphères (exercice 7.7). En
tant que tel, ∆k donne les ﬂuctuations locales sur l’échelle 1/k alors que l’intégrale (7.51) inclut les
contributions provenant de la comparaison de sphères distantes.
ÉC
E
Le spectre des ﬂuctuations de densité
N
H
EC
E
U
IQ
285
et les connecter avec les mesures d’anisotropie du CBR. Pour k < 0.01h Mpc−1 , les
mesures du CBR indiquent que ∆k ∝ k 2 ∝ R−2 .
Alors que l’amplitude du spectre dépend fortement du type d’objet que l’on observe, on voit que la forme du spectre est relativement insensible au type d’objet.
Nous verrons dans la section 6 que, dans le modèles de matière noire froide, la forme
du spectre est déterminée par le paramètre Γ = ΩM h. La forme du spectre pour tous
les types de galaxies est en faveur de Γ ∼ 0.25 ce qui implique
ÉC
E
L
O
T
Y
L
PO
ΩM h70 ∼ 0.37 .
(7.55)
Les modèles avec ΩM ∼ 1 sont donc écartés.
On a l’habitude de donner la normalisation du spectre en termes de σ8 = ∆MR /MR
pour R = 8h−1 Mpc. Les ﬂuctuations des données de galaxies observées optiquement
dans la ﬁgure 7.4 indiquent [150]
σ8 ∼ 1.0
galaxies sélectionnées optiquement .
N
H
EC
E
U
IQ
(7.56)
De l’information indépendante de biais sur les inhomogénéités de densité peut être
obtenue à partir du comptage des amas de galaxies. Les plus grands amas ont des
masses de l’ordre de la masse moyenne contenue dans une sphère de rayon 8h−1 Mpc
et il n’est pas surprenant que le nombre volumique d’amas, ncl , soit relié d’une façon
ou d’une autre à σ8 . Considérons une époque t1 avant la formation des amas. Caractérisons cette époque par ΩM (t1 ) et σ8 (t1 ), en ignorant pour simpliﬁer l’existence
d’énergie du vide. Par σ8 (t1 ) nous entendons, bien sûr, les ﬂuctuations de masse dans
des sphères de rayon 8âh−1 Mpc. La théorie gravitationnelle standard (Sect. 3) nous
permet de déterminer σ8 (t0 ) à partir de ces deux paramètres. Par exemple, nous avons
déjà vu que σ8 croît linéairement avec a(t) tant que σ8 1 et que ΩT = ΩM =∼ 1.
De façon générale, on écrit
ÉC
E
L
O
T
Y
L
PO
σ8 (t0 ) = f (σ8 (t1 ), ΩM (t1 )) = f˜(σ8 (t1 ), ΩM (t0 )) ,
(7.57)
où, dans la seconde forme nous faisons usage de ce que ΩM (t1 ) détermine ΩM (t0 ). Le
nombre d’amas qui seront formés plus tard, peut être estimé en fonction de σ8 (t1 ) et
ΩM (t1 ) en utilisant le modèle d’eﬀondrement sphérique de la section 1 ou une variante
plus sophistiquée (le modèle de Press–Schechter ou des simulations numériques à Ncorps). Dans ces modèles, on a besoin des deux paramètres puisque ΩM (t1 ) détermine
la grandeur d’une ﬂuctuation de densité nécessaire pour former une région d’énhergie
négative alors que σ8 (t1 ) donne la probabilité qu’une telle ﬂuctuation se produise.
(Nous supposons que les ﬂuctuations de masse sont gaussiennes.) On peut donc écrire
formellement
Y
L
PO
H
C
TE
ncl (t0 ) = g(σ8 (t1 ), ΩM (t1 )) = g̃(σ8 (t1 ), ΩM (t0 )) .
U
Q
I
N
(7.58)
En combinant ces deux expressions, on peut formellement éliminer σ8 (t1 ) en faveur
de σ8 (t0 )
ÉC
E
L
O
ncl (t0 ) = h(σ8 (t0 ), ΩM (t0 )) .
(7.59)
E
286
ÉC
E
U
IQ
Chapitre 7. La formation des structures
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
T
Y
L
PO
N
H
EC
E
U
IQ
U
Q
I
N
Fig. 7.4: Compilation de mesures de ∆k utilisant le comptage de galaxies et d’amas (Abell)
H
C
TE
de galaxies [145]. Le panneau supérieur montre les mesures brutes. La normalisation de ∆k
obtenue avec diﬀérents traceurs varie d’un facteur ∼ 5. Les amas de galaxies sont les plus
inhomogènes. On pouvait s’y attendre puisque les amas correspondent à des ﬂuctuation de
densité élevées et sont donc très sensibles à la densité moyenne locale. Les galaxies plus
communes sélectionnées optiquement (CfA,APM) et les galaxies sélectionnées dans l’infrarouge (IRAS) constituent les traceurs les plus homogènes. Alors que la normalisation varie
selon le traceur, la forme du spectre est relativement constante. Le panneau du bas montre le
spectre après que l’on a renormalisé chaque traceur par un facteur relatif de biais de façon
que l’abscisse puisse être interprétée comme (bI ∆k )2 où bI est un facteur de biais pour les
galaxies infrarouges. Les points sur le panneau du bas sont également corrigés pour les eﬀets
non-linéaires qui apparaissent quand on fait la transformation de l’espace du redshift à l’espace réel. Les courbes sont les prévisions de modèles avec de la matière noire froide (Sect. 6)
paramétrisée par Γ = ΩM h. Les données suggèrent ΩM h ∼ 0.25 (ΩM h70 ∼ 0.37). Avec la
permission de J. Peacock et Cambridge University Press.
ÉC
E
L
O
Y
L
PO
E
Le spectre des ﬂuctuations de densité
T
Y
L
PO
N
H
EC
E
U
IQ
287
Une mesure de ncl donne alors des contraintes sur σ8 (t0 ) et ΩM (t0 ). Il se trouve que
ncl est en bonne approximation fonction d’une combinaison particulière :
E
L
O
ncl (t0 ) ∼ h̃(σ8 Ω0.56
M ),
(7.60)
où nous omettons l’argument t0 . Cette formule nous dit qu’un faible σ8 combiné avec
ΩM = 1 donne le même nombre d’amas qu’un fort σ8 et un faible ΩM . Dans le
premier cas une petite ﬂuctuation de densité suﬃt à former un amas, alors que dans
le deuxième cas il en faut une grande.
Des mesures récentes [103] donnent σ8 Ω0.56
M ∼ 0.5. En prenant ΩM ∼ 0.3 d’après
la fraction baryonique des amas, cela donne σ8 ∼ 0.7.
Les mesures du nombre volumique des amas peuvent donner séparément ΩM et
σ8 si la densité peut être mesurée en fonction du temps ou, de façon plus réaliste, en
fonction du redshift. L’évolution du nombre d’amas dépend de ΩM car la formation des
structures se ralentit à acΛ = ΩM /(1−ΩM ) pour ΩΛ = 0 et à acΛ = (ΩM /(1−ΩM ))1/3
pour ΩT = 1. Le petit taux d’évolution que montre la ﬁgure 7.5 indique [103]
ÉC
N
H
EC
E
U
IQ
ΩM = 0.49 ± 0.12
σ8 = 0.72 ± 0.10
ΩΛ = 0
ΩM = 0.44 ± 0.12
σ8 = 0.77 ± 0.15
ΩT = 1 .
et
E
L
O
T
Y
L
PO
(7.61)
(7.62)
On voit que l’évolution du comptage des amas de galaxies donne une valeur de
ΩM presque indépendante de ΩΛ . Elle est légèrement supérieure à celle trouvée par
d’autres méthodes mais compatible avec elles.
Finalement, mentionnons que le spectre des ﬂuctuations de densité peut être mesuré par l’eﬀet de lentille gravitationnelle de la structure à grande échelle. Comme
nous l’avons discuté dans la section 8, les inhomogénéités de densité engendrent des
corrélations entre l’orientation apparente des galaxies proches les unes des autres dans
le ciel. Cette méthode a l’avantage d’être indépendante de biais et de la théorie de
formation des amas. Les premières mesures de cet eﬀet [117] donnent des résultats
compatibles avec ceux de méthodes traditionnelles.
En plus des inhomogénéités de densité, il y a aussi des « inhomogénéités de vitesse », c’est-à-dire des vitesses particulières. La seule galaxie pour laquelle on a bien
mesuré sa vitesse particulière est la nôtre. Sa vitesse peut être déduite des anisotropies
du CBR. Soit un observateur A qui voit une température du CBR isotrope. Un autre
observateur B en mouvement avec une vitesse v c par rapport à A verra (exercice 7.3) une température qui dépend de l’angle θ entre la direction d’observation et
v :
v
(7.63)
T (θ) = T0 1 + cos θ .
c
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
Les observations indiquent que le système solaire se déplace à une vitesse de 371 km s−1
à peu près dans la direction de la constellation de la Vierge [146]. En soustrayant la
ÉC
E
288
ÉC
E
U
IQ
Chapitre 7. La formation des structures
E
L
O
T
Y
L
PO
N
H
EC
n(>kT) (h3 Mpc-3)
10-5
FLAT MODEL Ω0 = 0.44
10-6
10-7
ÉC
10-8
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
z = 0.05
z = 0.38
2
10
kT (keV)
Fig. 7.5: Nombre volumique d’amas avec des températures de rayons X supérieures à T
en fonction de T [103]. Les données sont montrées pour deux plages de redshifts autour de
z ∼ 0.05 et de z ∼ 0.38. La petite diﬀérence dans le nombre d’amas est compatible avec ce
que l’on attend pour un univers avec ΩM ∼ 0.45 indépendant de ΩΛ .
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Évolution newtonienne
T
Y
L
PO
N
H
EC
E
U
IQ
289
vitesse orbitale du système solaire autour du centre galactique et la vitesse de la Voie
Lactée dans le groupe local de galaxies, on trouve que le groupe local a une vitesse par
rapport au CBR de (627 ± 22) km s−1 dans une direction d’à peu près 45 degrés par
rapport à celle de l’amas voisin de la Vierge. Cette vitesse peut être identiﬁée avec la
vitesse particulière du groupe local. On peut en conclure que les vitesses particulières
des amas sont de l’ordre de 10−3 c.
Le mouvement particulier radial d’autres galaxies peut être estimé à partir des
déviations à la loi de Hubble :
ÉC
E
L
O
vp = cz − H0 R
z1,
(7.64)
où la « distance » R de la galaxie est mesurée, par exemple, par la relation de Tully–
Fisher. Comme il s’agit de la diﬀérence entre deux grands nombres dont l’un est
diﬃcile à mesurer, il n’est par surprenant que les mesures de vitesses particulières de
galaxies lointaines ne soient pas très précises.
Comme pour les inhomogénéités de densité, la vitesse particulière est très intéressante si on la moyenne sur un volume contenant plusieurs galaxies, ce qu’on appelle
les « ﬂots globaux ». Le fait de moyenner a pour eﬀet d’éliminer les vitesses aléatoires dues au mouvement orbital dans les amas liés. Par exemple, (7.42) suggère que
la vitesse radiale particulière sur la surface d’une sphère de rayon R est
E
L
O
T
Y
L
PO
vp ∼ (1/3) Ω0.6
M δR
ÉC
N
H
EC
R
dH
E
U
IQ
ΩΛ = 0 ,
(7.65)
où le contraste de densité δ est moyenné sur le volume. Pour R 10h−1 Mpc, δ ∝ R−2
et l’on s’attendrait à ce que les vitesses moyennes décroissent en R−1 . Ce résultat peut
se généraliser à une énergie du vide non-nulle [147]. Comme nous l’avons déjà souligné,
ces relations montrent que les Ω pourraient être déterminés avec précision si les vitesses
particulières et les contrastes de densité pouvaient être mesurés précisément [143].
3
Évolution newtonienne
Le modèle d’eﬀondrement sphérique est relativiste mais il se limite au cas d’une
pression nulle et d’une symétrie sphérique. Dans cette section nous présentons le
t), une
traitement standard newtonien d’un ﬂuide caractérisé par une densité ρ(R,
t), une vitesse du ﬂuide v (R,
t), et un potentiel gravitationnel Φ(R,
t).
pression p(R,
L’hypothèse qu’il y a une seule vitesse par point, v (R, t), nous limite soit au cas d’une
pression nulle (dispersion en vitesse nulle) ou au cas d’un ﬂuide parfait (libre parcours
t) est la vitesse collective du
moyen nul des particules). Dans le deuxième cas, v (R,
ﬂuide. L’utilisation d’un potentiel gravitationnel nous limite au cas d’un gaz nonrelativiste. Bien que cette analyse ne s’applique pas directement au plasma photonbaryon relativiste, elle donne néanmoins des résultats qualitatifs corrects.
Si on l’applique au cas d’une pression nulle, notre formalisme newtonien va conﬁrmer nos conclusions sur le taux de croissance des inhomogénéités que nous avons
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
290
E
U
IQ
Chapitre 7. La formation des structures
T
Y
L
PO
N
H
EC
trouvées avec le modèle d’eﬀondrement sphérique. Appliqué au cas d’une pression
non-nulle, nous allons montrer que dans certaines circonstances les inhomogénéités de
densités se propagent comme des ondes acoustiques de vitesse
ï ò
dp
.
(7.66)
c2s =
dρ adiabatique
ÉC
E
L
O
Pour un ﬂuide parfait, les ondes sont adiabatiques car le libre parcours moyen nul
des particules empêche la diﬀusion de particules ou de chaleur. Nous verrons que la
propagation d’ondes est possible seulement si la longueur d’onde est inférieure à la
longueur d’onde de Jeans :
2π
cs
λj = 2π √
= c s tH ,
4πGρ̄
3/2
(7.67)
E
U
IQ
où dans la deuxième forme nous avons utilisé l’équation de Friedmann
pour k = 0.
√
Pour un gaz relativiste p = ρ/3, et la vitesse du son est cs = c/ 3. Il s’ensuit que la
longueur de Jeans est d’ordre dH . On peut donc s’attendre à ce que pendant l’époque
de rayonnement, le ﬂuide constitué de photons et de particules chargées va transmettre
des ondes acoustiques, inhibant la croissance de structures aux échelles inférieure à
celle de Hubble. À cause de leur grand libre parcours moyen, les wimps et les neutrinos
ne participent pas à la propagation d’ondes mais, comme ils ne constituent pas la
composante dominante de l’énergie pendant l’ époque du rayonnement, la croissance
des inhomogénéités de densité de wimps ou de neutrinos est encore inhibée.
Pour un gaz non-relativiste gas, on a cs c et λj dH . Il s’ensuit que l’on peut
de façon générale ignorer les ondes acoustiques pendant l’époque de matière.
Le fait que les perturbations de longueur d’onde inférieure à la longueur de Jeans
oscillent comme des ondes acoustiques au lieu de s’eﬀondrer gravitationnellement n’est
pas surprenant (Fig. 7.6). Nous avons vu dans le modèle d’eﬀondrement sphérique
qu’une petite sur-densité δ croît en proportion du paramètre d’échelle a(t) ce qui
signiﬁe que le temps caractéristique pour accroître signiﬁcativement δ est le temps
de Hubble tH . D’un autre côté, en l’absence de gravitation, une région sur-dense de
taille λ va engendrer une onde acoustique qui va disperser la sur-densité dans un
temps ts ∼ λ/cs . La condition que δ croisse par eﬀondrement gravitationnel plus
rapidement qu’il n’est dispersé par le rayonnement acoustique est ts > tH ce qui
équivaut à λ > λj .
Faisons maintenant l’analyse standard de Jeans pour un ﬂuide non-relativiste dans
un univers en expansion. Les trois équations qui déterminent le comportement d’un
ﬂuide parfait en gavitation sont la conservation de la masse
ÉC
E
L
O
T
Y
L
PO
N
H
EC
∂ρ
· (ρv ) = 0 ,
+ ∇
∂t
Y
L
PO
H
C
TE
la force gravitationnelle et hydrodynamique sur un élément de volume
ï
ò
∂v
− ρ∇Φ
,
ρ
+ (v · ∇)v = −∇p
∂t
ÉC
E
L
O
U
Q
I
N
(7.68)
(7.69)
E
Évolution newtonienne
ÉC
E
L
O
T
Y
L
PO
N
H
EC
t
291
t + λ/ c s
λ
ÉC
E
U
IQ
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
t + tH
Fig. 7.6: Le temps caratéristique pour la croissance gravitationnelle d’une sur-densité est
le temps de Hubble. Le temps caratéristique pour sa dispersion par la formation d’ondes
acoustiques est λ/cs . Le temps de dispersion est plus grand que le temps de croissance si
λ > λj .
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
292
E
U
IQ
Chapitre 7. La formation des structures
T
Y
L
PO
N
H
EC
et l’équation de Poisson pour un potentiel gravitationnel
∇2 Φ = 4πGρ .
E
L
O
(7.70)
Pour ce traitement newtonien, toutes les équations sont écrites dans les coordonnées
du laboratoire.
La solution de ces trois équations qui correspond à un univers homogène dominé
par la matière est :
ÉC
ρ = ρ(t0 )â−3
v =
ȧ R
a
Φ =
4πGρ 2
|R| ,
6
(7.71)
où a(t) satisfait l’équation de Friedmann . Le fait que la vitesse et le potentiel devien√
nent de l’ordre de 1 quand la distance à l’origine devient de l’ordre de dH ∼ 1/ Gρ
signiﬁe que ce formalisme non-relativiste ne peut traiter que des perturbations sur
des échelles bien inférieures à dH .
À la solution ci-dessus, nous ajoutons maintenant une petite perturbation de densité sous la forme d’une onde proportionnelle au paramètre d’échelle :
åô
ñ
Ç
−i k · R
−3
,
(7.72)
1 + δk (t) exp
ρ = ρ(t0 )â
â(t)
ÉC
E
L
O
T
Y
L
PO
λk (t) =
N
H
EC
E
U
IQ
2π
â(t) .
k
(7.73)
Le vecteur d’onde k est ﬁxe. La perturbation décrit le contraste de densité sur l’échelle
de 1/k (aujourd’hui). Une perturbation de densité perturbe en général la pression :
å
Ç
−i k · R
2
−3
p = p̄(t) + cs ρ(t0 )â δk (t) exp
,
(7.74)
â(t)
où nous avons utilisé la déﬁnition (7.66) de la vitesse du son. Les perturbations dans
le champ de vitesse et dans le potentiel sont déﬁnies par
Ç
å
−i k · R
ȧ v = R + vk (t) exp
,
(7.75)
a
â(t)
et
4πGρ 2
k (t) exp
r + Φ
Φ =
6
Ç
H
C
TE
−i k · R
â(t)
Y
L
PO
å
.
U
Q
I
N
(7.76)
En substituant ρ, p, v et Φ dans (7.68), (7.69) et (7.70), nous trouvons
ÉC
E
L
O
δ̇k −
i k · vk
= 0,
â(t)
(7.77)
E
Évolution newtonienne
N
H
EC
E
U
IQ
d(âvk )
− i k(c2s δk + Φk ) = 0 ,
dt
et
ÉC
E
L
O
T
Y
L
PO
Φk = −
293
(7.78)
4πGρ̄
δk .
(k/â)2
(7.79)
Si vk ⊥ k, il découle de (7.78) que d(âvk )/dt = 0 ce qui implique que l’amplitude
de la perturbation décroît avec le temps, vk ∝ 1/a. Nous pouvons donc en général
ignorer ces modes « transverses » et supposer que vk k. Dans ce cas, (7.77) devient
δ̇k = −i(k/â)vk .
(7.80)
Cette équation est équivalente à (7.42), trouvée avec le modèle d’eﬀondrement sphérique.
En substituant (7.80) et (7.79) dans (7.78), on trouve une équation diﬀérentielle
du second ordre pour δk :
N
H
EC
ȧ
δ̈k + 2 δ̇k + (c2s (k/â)2 − 4πGρ̄)δk = 0
a
ou, de façon équivalente,
ÉC
E
L
O
T
Y
L
PO
E
U
IQ
ȧ
δ̈k + 2 δ̇k + c2s [(k/â)2 − kj2 ]δk = 0 ,
a
(7.81)
où kj = 2π/λj .
Les solutions de (7.81) dépendent de la valeur du nombre d’onde k/â comparé
au nombre d’onde de Jeans kj . Pour de courtes longueur d’ondes, λk â λj , (7.81)
prend la forme
ȧ
δ̈k + 2 δ̇k + c2s (k/â)2 δk = 0
a
cs k/â 4πGρ̄ ∼ ȧ/a .
(7.82)
C’est là l’équation d’une onde acoustique amortie par l’expansion de l’univers. Pour
ȧ/a → 0, la solution est
t
cs dt
.
(7.83)
Θ(t) = k
δk ∼ exp(±iΘ)
â
Pour de grandes longueur d’ondes, λk â λj , (7.81) prend la forme
ȧ
δ̈k + 2 δ̇k − 4πGρ̄δk = 0
a
H
C
TE
cs k/â 4πGρ̄ .
Y
L
PO
U
Q
I
N
(7.84)
Comme d’habitude, la situation devient plus claire si l’on utilise â(t) comme variable
indépendante. Dans le cas ΩM = ΩT = Ω, on trouve
[Ω + (1 − Ω)â] â2
ÉC
E
L
O
dδk
d2 δk
+ [3Ω/2 + 2(1 − Ω)â] â
− [3Ω/2] δk = 0 .
dâ2
dâ
(7.85)
E
294
E
U
IQ
Chapitre 7. La formation des structures
T
Y
L
PO
N
H
EC
Il y a deux solutions correspondant à des modes croissants ou décroissants. Pour
Ω = 1, les solutions sont
δk ∝ a ,
E
L
O
δk ∝ a−3/2
(ΩM = ΩT = 1) .
(7.86)
δk ∝ a−1
(ΩM = ΩT = 0) .
(7.87)
Pour Ω = 0 les solutions sont
ÉC
δk ∝ a0 ,
Les modes croissants conﬁrment le comportement aux temps longs trouvé dans le
modèle d’eﬀondrement sphérique, par exemple ∆ρ/ρ ∝ a pour ΩM = ΩT = 1.
Enﬁn, on note la solutions de (7.84) dans la limite ȧ/a → 0 :
ã
Å
ȧ
−2
δk ∝ exp(±t/τ )
=0 .
(7.88)
τ = 4πGρ̄
a
N
H
EC
E
U
IQ
On voit que l’eﬀondrement gravitationnel du ﬂuide est, dans ce cas, exponentiel. Dans
un univers en expansion, l’eﬀondrement suit seulement une loi en puissances parce
que l’expansion agit contre l’eﬀondrement.
4
T
Y
L
PO
Entrée et sortie du rayon de Hubble
E
L
O
Comme nous l’avons souligné, tant que le contraste de densité est faible, les région sur-denses participent à l’expansion et l’extension spatiale des perturbations de
densité croît à peu près comme le paramètre d’échelle :
ÉC
λk (a) = λk (a0 )â =
2π
â .
k
(7.89)
D’un autre côté, la distance de Hubble croît comme a2 pendant l’époque du rayonnement et comme a3/2 pendant l’époque de matière :
−1/2
dH (a) = H0−1 â2 1.68Ωγ + ΩM â + ΩΛ â4 + (1 − ΩT )â2
.
(7.90)
En outre, si l’univers a traversé une époque inﬂationnaire précoce, la distance de
Hubble était relativement constante avant l’époque du rayonnement :
Å
dH ∼
8πGV (φ)
3
ã−1/2
H
C
E
a2 < a < a1 ,
T
Y
POL
U
Q
I
N
(7.91)
où V (φ) est le potentiel du champ φ qui actionne l’inﬂation, et a2 et a1 correspondent
au début et à la ﬁn de l’inﬂation comme l’illustre la ﬁgure 5.8. Cette séquence est
illustrée sur la ﬁgure 7.7.
Les modes intéressants (exercice 7.8) étaient à l’intérieur du rayon de Hubble au
début de l’inﬂation, ils sont « sortis du rayon de Hubble » à l’instant tsortie , puis
ÉC
E
L
O
E
Entrée et sortie du rayon de Hubble
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
295
log(length)
log a(t)
−1
k c a(t)
−1
k b a(t)
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
dH
−1
k a a(t)
a exit
( kb )
a exit
( ka )
a1
inflation
end
a enter
( ka )
a eq
a enter
( kb )
a cΛ
Fig. 7.7: La distance de Hubble dH dans un modèle avec inﬂation. Une échelle physique
commence à l’intérieur du rayon de Hubble, le quitte à aexit et y rentre à aenter . Les petites
échelles sortent les dernières et rentrent les premières. Le mode ka est entré pendant l’époque
du rayonnement et le mode kb pendant l’époque de matière. Le mode kc n’est pas encore entré
et ne le fera jamais si l’énergie du vide continue à dominer.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
296
E
U
IQ
Chapitre 7. La formation des structures
N
H
EC
sont « entrés dans le rayon de Hubble »3 à l’instant tentrée :
T
Y
L
PO
λk (aentrée ) = dH (aentrée ) .
E
L
O
(7.92)
Sur la ﬁgure 7.7, il est clair que les petites longueur d’ondes entrent dans le rayon de
Hubble pendant l’époque du rayonnement, aentrée < aeq . En égalant (7.89) et (7.90)
on trouve
ÉC
λk (a0 ) 1.68Ωγ
H0−1
âentrée =
λk (a0 ) λeq .
(7.93)
Les modes de grande longueur d’onde entrent dans l’époque de matière, aentrée > aeq :
Ç
âentrée =
λk (a0 )
H0−1
å2
E
U
IQ
λk (a0 ) λeq .
ΩM
N
H
EC
(7.94)
La frontière entre grandes et faibles longueur d’ondes, λeq , correspond aux modes
qui entrent à teq :
λeq = H0−1
ÉC
E
L
O
keq =
T
Y
L
PO
1.68Ωγ /2
28h−1
14h−1 Mpc
70 Mpc
=
=
ΩM
ΩM h70
ΩM h
(7.95)
2π
= 0.224 ΩM h270 Mpc−1 = 0.45 h Mpc−1 ΩM h .
λeq
(7.96)
Pour aeq , nous avons supposé qu’il y a trois espèces de neutrinos de masse < 1 eV. Le
plus grand amas de galaxies correspond à k −1 ∼ 10h−1
70 Mpc qui est un peu plus petit
−1
que keq
∼ 15h−1
70 Mpc si ΩM h70 ∼ 0.3.
Nous verrons dans la section 6 que keq donne l’échelle à laquelle le spectre ∆k
(Fig.7.4) commence à s’aplatir.
Pendant le temps entre tsortie et tentrée , un mode va évoluer de façon simple car
une grande longueur d’onde permet de négliger les dérivées spatiales dans les équations
et tous les eﬀets de microphysique. Comme nous l’avons souligné, l’évolution précise
dépend de notre choix de coordonnée temporelle puisque ∆k compare des densités
en des points largement séparés qui ne sont pas en communication. En coordonnées
comobiles (ce qu’on appelle la « jauge synchrone »), le contraste de densité suit
des lois en puissances simples que l’on peut trouver en comparant des équations de
Friedmann indépendantes comme nous l’avons fait dans le modèle d’eﬀondrement
sphérique (Section 1.3 et exercice 7.2). Pour l’époque de matière nous avons trouvé
∆k ∼ a
Y
L
PO
asortie < a < aentrée
E
L
O
H
C
TE
époque de matière .
U
Q
I
N
(7.97)
3 Traditionnellement, on dit « entrer dans l’horizon », une expression qui date de l’époque où l’on
pensait que l’horizon était de l’ordre de dH . Dans les modèles inﬂationnaires, ce n’est pas le cas et
nous préférons dire « entrer dans le rayon de Hubble”.
ÉC
E
Entrée et sortie du rayon de Hubble
T
Y
L
PO
N
H
EC
E
U
IQ
297
Dans un univers dominé par la matière, on observe ce comportement que le mode soit
à l’intérieur ou à l’extérieur du rayon de Hubble (tant que ∆k 1).
Pendant l’époque du rayonnement, les modes super-Hubble croissent plus rapidement (7.43) :
ÉC
E
L
O
∆k ∼ a2
asortie < a < aentrée
époque de rayonnement .
(7.98)
Lorsque les modes sont à l’intérieur du rayon de Hubble, l’évolution est aﬀectée par la
microphysique comme les oscillations acoustiques ou l’écoulement libre de particules.
Enﬁn, pendant l’époque inﬂationnaire, si V (φ) est presque constant, le contraste
de densité décroît avec le temps :
∆k ∼ a−2
époque de l inﬂation .
asortie < a < aentrée
(7.99)
E
U
IQ
Pour voir comment cela se produit, considérons un modèle à symétrie sphérique avec
une région centrale où il y a une ﬂuctuation de densité positive. La ﬂuctuation de
densité provient de ce que le champ central φc est initialement plus haut sur la colline
du potentiel que le champ moyen φ. Le paramètre d’échelle moyen a(t) et le paramètre
d’échelle central ac (t) obéissent (7.15) et (7.17). L’évolution de φ et φc est régie par
la condition de « descente lente » (5.58) :
T
Y
L
PO
V
φ̇ =
3H
ÉC
E
L
O
φ̇c =
N
H
EC
V
.
3Hc
(7.100)
Le terme de courbure dans l’équation de Friedmann pour ac va réduire le taux d’expansion central si bien qu’initialement Hc < H. Il s’ensuit que |φ̇c | > |φ̇| et φc descend
plus vite la pente de potentiel en essayant de rattrapper φ. On peut démontrer de
façon simple que l’équation suivante régit la diﬀérence de champ :
ï
ò
d(φ − φc )
V
8πG
2 −2
=
(φ
−
φ
ã
(Ω
−
1)
+
)V
H
.
(7.101)
1c
c
1c
dt
6H 3
3
La solution est
|φc − φ| ∝ a−2 ,
(7.102)
U
Q
I
N
si ȧ/a ∼constante. Cela implique alors ∆k ∝ a−2 puisque ∆ρ = V × (φc − φ).
Bien entendu, tout ce discours sur l’évolution hors du rayon de Hubble peut sembler très académique. Après tout, on ne peut pas mesurer ce qui se passe hors du rayon
de Hubble aujourd’hui. Ce qui fait l’intérêt de l’étude de l’évolution super-Hubble est
que pendant l’époque inﬂationnaire, les échelles intéressantes étaient initialement dans
le rayon de Hubble, qu’elles en sont sortie à tsortie et y sont revenues à tentrée . Dans
de tels modèles, les ﬂuctuations initiales peuvent être imposées de façon causale avant
tsortie . En suivant les ﬂuctuations hors du rayon de Hubble, on peut prévoir les ﬂuctuations observées actuellement. Nous allons montrer comment cela se fait dans les
deux sections suivantes.
ÉC
E
L
O
Y
L
PO
H
C
TE
E
298
5
E
U
IQ
Chapitre 7. La formation des structures
N
H
EC
Le spectre primordial
T
Y
L
PO
Les sections précédentes ont montré comment ∆k évolue dans le temps. Le dernier
élément dont nous ayons besoin pour prévoir le spectre de ﬂuctuations de densité
d’aujourd’hui est le spectre « primordial ». Ce que l’on appelle « primordial » dépend
des ambitions que l’on a. Ce terme se réfère souvent à un temps pendant l’époque du
rayonnement lorsque les modes qui nous intéressent étaient hors du rayon de Hubble.
Toutefois, nous allons voir que le spectre peut être relié à des conditions antérieures,
pendant l’époque inﬂationnaire.
Comme nous le verrons en section 9, les anisotropies observées du CBR sont interprétées principalement comme indiquant que les ﬂuctuations primordiales étaient
adiabatiques, c’est-à-dire que ce sont de pures ﬂuctuations de densité. Nous pouvons
donc spéciﬁer les conditions initiales par la fonction ∆k (a < aentrée ). Puisque l’univers apparaît homogène à grande échelle, on peut supposer que le spectre primordial
est de la forme :
ÉC
E
L
O
∆k (a < aentrée ) ∝
1
∝ k
β
HN
β>0.
C
E
T
LY
λβk
E
U
IQ
(7.103)
Puisque les modes super-Hubble évoluent comme ∆k ∼ an avec n = 2, 1, −2 pendant
les époques du rayonnement, de la matière et de l’inﬂation respectivement, la forme
du spectre est indépendante du temps en dehors du rayon de Hubble.
Nous verrons que les modèles inﬂationnaires prévoient β ∼ 2, et que cette prévision
est conﬁrmée par les anisotropies du CBR sur les échelles H0−1 > λk (a0 ) > 0.01H0−1 :
O
P
E
L
ÉCO
∆k ∝
1
∝ k2 .
λk (a0 )2
(7.104)
En l’absence de contre-indications empiriques ou observationnelles on peut supposer
que cette loi s’applique à toutes les échelles intéressantes.
Un spectre avec β = 2 est dit « invariant d’échelle » (ou encore spectre de
Harrison–Zel’dovich). L’invariance d’échelle réfère aux ﬂuctuations du potentiel newtonien Φ sur l’échelle R :
ï
ò
ï
ò
∆ρ
∆ρ
(4π/3)R3
G∆M
∼ Gρ
∼ Gρ
R2 .
(7.105)
∆ΦR ∼
R
ρ R
R
ρ R
U
Q
I
N
E
La ﬂuctuation du potentiel est indépendante de R si ∆ρ/ρ ∝ R−2 . On voit aussi
que ∆Φ est indépendant du temps puisque ρ ∝ a−n , ∆ρ/ρ ∝ an−2 , et R2 ∝ a2 où
n = 3, 4, 0 pour les époques de matière, de rayonnement et d’inﬂation respectivement.
Une caractéristique très importante d’un spectre invariant d’échelle est que ∆k (aentrée ) ≡
∆H est indépendant de k. En normalisant ∆k à une époque a1 < aentrée et en utilisant
(7.93) pour les modes avec aentrée < aeq , on trouve
E
L
O
Y
L
PO
∆H = ∆k (aentrée ) = ∆k (a1 )
ÉC
Å
H
C
TE
aentrée
a1
ã2
∝
1 2
λ ,
λ2k k
(7.106)
Le spectre primordial
T
Y
L
PO
N
H
EC
E
U
IQ
299
c’est-à-dire indépendant de k. ∆H est aussi indépendant de k pour les modes avec
aentrée > aeq :
ÉC
E
L
O
Å
∆H = ∆k (a1 )
aeq
a1
ã2 Å
aentrée
aeq
ã
1 2
λ .
λ2k k
∝
(7.107)
Le spectre des anisotropies du CBR (section 9) donne une valeur de ∆H qui dépend
des valeurs que l’on a choisies pour les Ω. Pour ΩM = 1 et ΩΛ = 0 les observations
de COBE indiquent [148, 159]
∆H = 2 × 10−5 ,
(7.108)
avec une incertitude d’environ 10%. D’autres valeurs raisonnables des Ω donnent des
valeurs de ∆H du même ordre de grandeur.
La quantité ∆H = 2 × 10−5 est le paramètre fondamental de la cosmologie
inhomogène invariante d’échelle. Elle détermine les quantités suivantes :
N
H
EC
– les ﬂuctuations de densité actuelles à grande échelle :
LY T
Å
∆k (a0 ) ∼ ∆H
O
P
E
L
ÉCO
dH
R
E
U
IQ
ã2
;
– l’échelle sur laquelle les ﬂuctuations sont de l’ordre de l’unité :
R(∆ ∼ 1) ∼ dH ∆H ∼ 13h−1 Mpc ;
(7.109)
(7.110)
– Les vitesses particulières maximum, c’est-à-dire celles sur l’échelle où δ ∼ 1, qui
sont d’après (7.40)
vp ∼
R
∼
∆H ∼ 4 × 10−3 c ;
dH
– les ﬂuctuations du potentiel newtonien sur l’échelle R
∆ΦR ∼ Gρ ∆H d2H ∼ ∆H ;
H
C
TE
(7.111)
U
Q
I
N
(7.112)
– les ﬂuctuations de la température du CBR sur une grande échelle angulaire
(Sect. 9) :
ÉC
E
L
O
Y
L
PO
∆T
∼ ∆H ;
T
(7.113)
E
300
E
U
IQ
Chapitre 7. La formation des structures
T
Y
L
PO
N
H
EC
– La dispersion en vitesses, ∆v, et la profondeur des puits de potentiel, Φ, d’objets
virialisés (7.27) sur des échelles (non eﬀondrées) λk (a0 ) > λeq :
ÉC
E
L
O
∆v 2
∼ Φ ∼ ∆H .
c2
(7.114)
Les amas de galaxies et les halos galactiques correspondent à des échelles plutôt
inférieures et, en tant que telles, elles ont des dispersions en vitesse plus petites
d’un facteur (∼ aentrée /aeq ) mais ∆H donne toujours le bon ordre de grandeur
de la vitesse quadratique de rotation dans les galaxies spirales, par exemple.
Les modèles inﬂationnaires donnent une explication naturelle pour le spectre invariant d’échelle observé. L’époque inﬂationnaire a une invariance temporelle dans
le sens où la densité d’énergie est assez constante dans le temps. La seule distance
caractéristique est la distance de Hubble indépendante du temps. Dans de telles circonstances, il est plausible que l’amplitude des ﬂuctuations sur l’échelle de la distance
de Hubble soit indépendante du temps :
N
H
EC
∆k (asortie ) ∼ constante .
T
Y
L
PO
E
U
IQ
(7.115)
C’est ce qui de produit approximativement dans les modèles inﬂationnaires où les
ﬂuctuations de densité peuvent être associées à des ﬂuctuations quantiques du champ
d’inﬂation φ. De telles ﬂuctuations ont une valeur moyennée sur un volume de Hubble
de
ÉC
E
L
O
2π
∼ H(tsortie ) ,
dH
∆φ ∼
(7.116)
qui peut être interprété comme une sorte de principe d’incertitude reliant l’incertitude
sur le champ et la taille de la région sur laquelle il est moyenné. L’inﬂation donne
alors naturellement un spectre de ﬂuctuations invariant d’échelle qui se réfère à tsortie
par
∆k (asortie ) ∼ V ∆φ ∼ [HV ]asortie .
(7.117)
Pour calculer la ﬂuctuation de densité à tentrée on remarque la circonstance heureuse que la décroissance des ﬂuctuations pendant l’inﬂation (7.99) compense la
croissance des ﬂuctuations pendant les époques de rayonnement (7.98) et de matière
(7.97) :
Å
ã2
a1
asortie
et
Å
ÉC
Å
∼
E
L
O
a1
asortie
Å
ã2
∼
aentrée
a1
ã2
Y
L
PO
aeq
a1
ã2
aentrée
aeq
H
C
TE
aentrée < aeq
aentrée > aeq
U
Q
I
N
(7.118)
(7.119)
E
Le spectre primordial
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
301
∆φ
V (φ)
ÉC
E
L
O
φ2
T
Y
L
PO
φ exit
N
H
EC
φ1
φ0
E
U
IQ
φ
Fig. 7.8: Un potentiel inﬂationnaire. Le champ descend la colline de potentiel jusqu’à ce
qu’il atteigne le minimum. L’inﬂation prend ﬁn à φ ∼ φ1 . Une région perturbée avec une
ﬂuctuation du champ ∆φ qui se situe plus haut dans le puits de potentiel va cesser son
inﬂation plus tard que la moyenne. Pour un temps plus court δt1 alors que la région perturbée
est toujours en inﬂation avec une densité d’énergie constante, le reste de l’univers est dans
l’époque du rayonnement avec une densité ρ ∝ a−4 . Lorsque la région perturbée arrêtera son
inﬂation, elle aura donc une densité de rayonnement plus grande que la moyenne, ∆ρ/ρ ∼
4H1 ∆t1 .
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
302
E
U
IQ
Chapitre 7. La formation des structures
T
Y
L
PO
N
H
EC
Cette compensation suggère que l’invariance d’échelle à tsortie va être transférée en
une invariance d’échelle à tentrée . Toutefois, avant d’en tirer des conclusions, il faut
être plus précautionneux sur l’évolution à la ﬁn de l’inﬂation.
Considérons une région A avec une ﬂuctuation de densité d’énergie positive due à
une ﬂuctuation du champ ∆φ. Comme l’illustre la ﬁgure 7.8, la région A quitte le rayon
de Hubble plus haut sur la colline de potentiel que dans les régions environnantes.
Comme l’inﬂation se termine lorsque le champ s’est retrouvé en φ1 , la région A termine
son inﬂation plus tard que le temps moyen t1 de la ﬁn :
ã
Å
∆φ
−V (φ)
,
(7.120)
∆t1 ∼
φ̇ ∼
3H
φ̇ t1
ÉC
E
L
O
où nous utilisons l’approximation de descente lente pour estimer φ̇. Dans la mesure
où le potentiel est constant, (7.102) implique que ∆φ(t1 ) ∼ ∆φ(tsortie )a2sortie /a21 .
À t1 , la région A est toujours en inﬂation avec une densité d’énergie à peu près
indépendante du temps, et le reste de l’univers est dominé par le rayonnement avec
une densité d’énergie qui décroît comme a−4 . Par conséquent, pendant le temps ∆t1
où la densité d’énergie de A reste constante, la densité d’énergie moyenne tombe de
∆ρ/ρ ∼ 4H1 ∆t1 ∼ 4H1 ∆φ/φ̇. Il s’ensuit que lorsque A arrête son inﬂation, il a une
ﬂuctuation de densité d’énergie positive
ï
ò
∆ρ
∆φ(t1 )
∆φ(tsortie ) a2sortie
∼ 4H1 ∆t1 ∼ 4H1
.
(7.121)
∼ 4H1
ρ t1
a21
φ̇
φ̇
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
La croissance des ﬂuctuations pendant l’époque de rayonnement et l’époque de matière
va compenser le facteur a2sortie /a21 si bien qu’en utilisant (7.116) on trouve
∆k (aentrée ) ∼
H2
2π φ̇
φ̇ ∼
−V (φ)
.
3H
(7.122)
Dans cette expression, nous n’essaierons pas de justiﬁer les facteurs numériques, et
nous ne nous sommes pas préoccupés de distinguer les paramètres du potentiel à tsortie
et t1 puisque nous avons supposé qu’ils étaient à peu près constants. Un traitement
plus complet d’un potentiel lentement variable [151] donnerait des ﬂuctuations de
densité à tentrée qui ne dépendent que du potentiel à tsortie .
ï 2ò
H
−V (φ)
.
(7.123)
∆k (aentrée ) ∼
φ̇ ∼
3H
2π φ̇ asortie (k)
H
C
TE
U
Q
I
N
Les échelles cosmologiquement intéressantes varient de ∼ 10−3 H0−1 à H0−1 ou
environ d’un facteur e10 . Puisque le nombre total de puissances de e pendant l’inﬂation
doit être au moins de ∼ 60, les modes intéressants sont sortis sur une partie assez
restreinte le l’époque inﬂationnaire totale et nous pouvons supposer que les paramètres
du potentiel ont peu varié sur cette intervalle de temps. C’est pour cette raison que
(7.123) donne un spectre presque invariant d’échelle, mais pas parfaitement.
ÉC
E
L
O
Y
L
PO
E
Modèles de matière noire froide
T
Y
L
PO
N
H
EC
E
U
IQ
303
Alors que l’inﬂation donne de façon naturelle un spectre de ﬂuctuations de densité
invariant d’échelle, l’amplitude des ﬂuctuations à l’entrée de Hubble est déterminée
par V (φ) et V (φ). Pour le moment, il n’existe pas d’argument convainquant pour
prévoir une valeur de ∆H proche de la valeur observée. Comme nous l’avons discuté
dans la section 5, cela peut être considéré comme un échec des modèles inﬂationnaires.
À cause de cela, il est normal de se poser la question de savoir si ∆H pourrait être
une variable déterminée par des eﬀets de sélection anthropique. Dans certains modèles,
∆H dépend de la position aux échelles super-Hubble, dans quel cas la probabilité
d’observer une valeur donnée de ∆H doit inclure des considérations anthropiques de
façon Bayesienne.
On montre facilement que les conditions locales sont fortement inﬂuencées par la
valeur de ∆H [152]. Si ∆H était plus petit que la valeur observée, la dispersion en
vitesse des objets virialisés serait plus faible. Si cette dispersion est trop faible, les
collisions atomiques inélastiques nécessaires au refroidissement radiatif ne sont pas
possibles. Il apparaît donc que la formation d’objets compacts comme les étoiles et
les planètes ne serait pas possible pour ∆H < 10−6 .
D’un autre côté, si ∆H était plus grand que la valeur observée, les objets virialisés
seraient plus denses. On estime que pour ∆H > 10−4 , les galaxies seraient suﬃsamment denses pour que les systèmes planétaires deviennent instables à cause des
rencontres stellaires proches. Cela éliminerait les conditions stables qui ont conduit à
l’évolution de la vie sur Terre. Pour ∆H > 10−2 , de grands nombres de trous noirs
sont formés ce qui limite le nombre de baryons disponibles pour l’apparition de la vie.
Il apparaît donc que ∆H et par conséquent le potentiel inﬂationnaire pourraient
être sujets à de forts eﬀets de sélection anthropique.
ÉC
E
L
O
ÉC
6
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
Modèles de matière noire froide
Nous possédons maintenant tous les éléments nécessaires pour comprendre qualitativement le spectre des ﬂuctuations de densité prévu par les modèles qui font appel
à de la matière noire froide et à un spectre primordial invariant d’échelle.
Les petites échelles pénètrent dans le rayon de Hubble pendant l’époque du rayonnement. Au cours de cette époque, les ﬂuctuations du plasma photons-particules chargées oscillent comme des ondes acoustiques amorties. Puisque cette composante domine gravitationnellement, il y a peu de croissance des ﬂuctuations de la composante
de matière noire froide par rapport à sa valeur à l’entrée du rayon de Hubble, ∆H . Dès
que la matière noire froide commence à dominer à teq , les ﬂuctuations se mettent à
croître linéairement avec le paramètre d’échelle. Dans l’approximation où l’on néglige
la croissance pendant l’époque du rayonnement, le spectre est indépendant de k :
Y
L
PO
∆k (a > aeq ) ∼ ∆H
ÉC
E
L
O
a
aeq
H
C
TE
k keq .
U
Q
I
N
(7.124)
À grande échelle, l’entrée dans le rayon de Hubble se passe à l’époque de matière. En
E
304
E
U
IQ
Chapitre 7. La formation des structures
T
Y
L
PO
N
H
EC
conséquence, les ﬂuctuations gardent leur spectre primordial :
a
∝ k2 ∝ λ−2
k keq ,
∆k (a > aeq ) = ∆H
k
aentrée
E
L
O
(7.125)
où nous utilisons la valeur de aentrée donnée par (7.94).
Pour améliorer ceci, il est nécessaire d’intégrer les équations d’Einstein et de Boltzmann de façon à tenir compte de la diﬀusion des particules et de la lente croissance
des ﬂuctuations de wimps pendant l’époque du rayonnement. Pour ∆k 1 et ΩΛ = 0,
le spectre calculé [153] pendant l’époque de matière est :
ÉC
∆k (a) ∼
1 + 0.765 kkeq
∆H H0−2 k 2 â
Ä ä3/2
Ä ä2 ,
+ 2.72 kkeq
+ 0.202 kkeq
où
keq = 0.45Γh Mpc−1
Γ = ΩM h .
N
H
EC
(7.126)
E
U
IQ
(7.127)
Le spectre prévu est montré sur la ﬁgure 7.9 pour â ∼ 0.1. Puisque les nombres
d’onde mesurés, k, sont proportionnelles à h, la fonction (7.126) est paramétrisée par
Γ = ΩM h et nous la montrons pour Γ = 0.21 et Γ = 0.7.
La normalisation de (7.126) est telle que ∆H0 (a0 ) ∼ ∆H . À petit k, ∆k augmente à
partir de cette valeur en suivant la forme primordiale ∝ k 2 jusqu’à ce qu’il se stabilise
à la valeur keq pour les modes tels que aentrée < aeq . Le spectre n’est pas plat pour
k > keq , comme le prévoit (7.124), à cause de la lente montée des ﬂuctuations des
wimps pendant l’époque du rayonnement mentionnée ci-dessus.
La normalisation de la courbe est proportionnelle à â. Dès que ∆k (a) approche
de l’unité à une échelle donnée, l’approximation linéaire n’est plus valable et des
structures commencent à se former autour des plus grandes ﬂuctuations de densité.
On voit sur la ﬁgure 7.9 que dans le cas Γ = 0.21, les galaxies (k ∼ h Mpc−1 ) sont
tout près de se former puisque ∆k ∼ 10−1 . Les amas de galaxies (k ∼ 0.1h Mpc−1 )
commencent à se former un peu plus tard.
La compilation des mesures de ∆k sur la ﬁgure 7.4 montre que les données sont en
accord avec le modèle de matière noire froide pour Γ ∼ 0.25, c’est-à-dire ΩM ∼ 0.37
si h ∼ 0.7. Un modèle avec ΩM ∼ 1 (Γ ∼ 0.7) prévoit de plus grandes ﬂuctuations
à petite échelle. Si la valeur de COBE ∆H = 2 × 10−5 est utilisée pour normaliser le
spectre à petit k, les ﬂuctuations prévues à k = 10h−1 Mpc pour ΩM = 1 sont à peu
près doubles des ﬂuctuations observées [154, 155]. Ces ﬂuctuations sont supprimées
dans un modèle avec ΩM ∼ 0.3 car l’époque de matière commence plus tard et les
oscillations acoustiques durent plus longtemps.
Comme le montre la ﬁgure 7.9, les modes de petite échelle peuvent également être
supprimés en utilisant un spectre primordial « penché » non-invariant d’échelle. Cela
permet de garder ΩM = 1, mais dans ce cas le modèle prévoit davantage d’évolution
dans le nombre volumique d’amas que ce que l’on observe [155].
Il y a une dizaine d’années, on croyait très généralement que ces observations
indiquant ΩM < 1 montraient que la prévision inﬂationnaire ΩT = 1 est incorrecte.
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Modèles de matière noire froide
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
T
Y
L
PO
E
U
IQ
N
H
EC
305
E
U
IQ
U
Q
I
N
Fig. 7.9: Fluctuations de densité ∆k prévues par les modèles faisant appel à de la matière
noire froide (7.126). La courbe montrée correspond à l’époque â = 0.1 et à ∆H = 2 × 10−5 ,
pour les valeurs Γ = ΩM h = 0.21 et Γ = 0.7. Les ﬂuctuations à grande échelle, k keq ,
ont le spectre primordial, ∆k ∝ k2 ∝ 1/λ2 . Les ﬂuctuations à petite échelle, k keq , sont
plus petites que les ﬂuctuations primordiales extrapolées car ces modes ont oscillé comme
des ondes acoustiques pendant l’époque du rayonnement. Nous avons également fait ﬁgurer
un modèle non-invariant d’échelle « penché » où le spectre à Γ = 0.7 a été multiplié par
(kH0−1 )−0.3 .
ÉC
E
L
O
Y
L
PO
H
C
TE
E
306
E
U
IQ
Chapitre 7. La formation des structures
T
Y
L
PO
N
H
EC
Les observations de supernovae et les mesures d’anisotropie du CBR ont fourni des
arguments expérimentaux en faveur de ΩΛ > 0 et ΩT ∼ 1, compatibles avec l’inﬂation.
Tandis que le modèle de matière noire froide avec (ΩM = 0.3, ΩΛ = 0.7) semble
s’accorder assez bien avec la plupart des observations, il faut souligner que ce modèle prévoit de plus grandes ﬂuctuations que ce qu’on observe à petite échelle, qui
correspond aux galaxies naines et aux cœurs galactiques [156]. Plusieurs auteurs ont
suggéré que c’est là l’indication d’une diﬃculté fondamentale des modèles qui utilisent
les wimps comme matière noire froide, mais cette proposition est contestée [157].
ÉC
7
E
L
O
Neutrinos et baryons
La seule justiﬁcation évidente de l’utilisation de particules de matière noire froide
dans la théorie de la formation des structures est que les modèles donnent un accord
comparativement bon avec l’observation. Puisque les particules de matière noire froide
n’ont pas encore été observées, il faut expliquer pourquoi on en a besoin. Il faut notamment expliquer les problèmes rencontrés dans les modèles qui utilisent seulement
les particules connues.
Un neutrino de masse ∼ 10 eV serait un candidat naturel pour la matière noire.
L’expérience (Sect. 1.5) ne penche pas pour des masses de neutrinos aussi grandes,mais
cette possibilité n’est pas complètement exclue. Comme les particules de matière noire
froide, les neutrinos ne participent pas aux oscillations acoustiques du plasma photonsparticules chargées, puisqu’ils se sont découplés à T ∼ MeV. Ils peuvent donc créer
librement des structures gravitationnelles dès qu’ils dominent la densité d’énergie à
teq sans être gênés par la présence du plasma relativiste photons-baryons.
Le problème avec les neutrinos est qu’ils sont relativistes entre le découplage T ∼
MeV et T ∼ mν . Pendant ce temps, les ﬂuctuations de densité de petite échelle de
neutrinos sont détruites car ils se propagent librement de régions de grande densité à
des régions de faible densité. Ce phénomène est appelé « l’écoulement libre ». Parce
que les neutrinos étaient relativistes lorqu’ils se sont découplés, la matière noire de
neutrinos est appelée « matière noire chaude ». Les particules de matière noire froide
étaient, par déﬁnition, non-relativistes quand elles se sont découplées et l’écoulement
libre est sans importance.
On peut calculer l’échelle λfs (écoulement libre ou « free streaming ») sur laquelle
les ﬂuctuations sont détruites en calculant la distance qu’un neutrino parcourt entre
T ∼ MeV (t = tf ) et T ∼ mν (t = tν ). La coordonnée distance est
tν
v(t)dt
χfs =
,
(7.128)
a(t)
tf
ÉC
E
L
O
T
Y
L
PO
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
où v(t) est la vitesse du neutrino. Dans l’approximation v(t) ∼ 1, elle est de l’ordre
de la distance de Hubble à tν :
ÉC
E
L
O
H −1
a(tν )χfs ∼ 0
â2ν ,
1.68Ωγ
(7.129)
E
Neutrinos et baryons
N
H
EC
E
U
IQ
307
où âν ∼ Tγ (t0 )/mν . Cela correspond à une distance aujourd’hui a0 χfs de
E
L
O
T
Y
L
PO
λfs ∼ 60 Mpc
10 eV
.
mν
(7.130)
Les ﬂuctuations sur des échelles plus courtes que cela sont eﬀacée par l’écoulement
libre si bien que
ÉC
∆k (aentrée ) ∼ 0
λk (a0 ) < λfs .
(7.131)
Pour de plus grandes échelles, λk > λfs , le spectre des ﬂuctuations est essentiellement
le même que pour de la matière noire froide.
Toutes les structures virialisées que l’on a observé correspondent à des échelles
inférueres à λfs pour des masses de neutrinos de quelques eV. Dans les modèles de
matière noire chaude, la seule façon de former de telles structures est par fragmentation de structures de plus grande écheelle. 4 De façon générale, cela mène à une
formation assez tardive des galaxies vers z ∼ 1, ce qui est diﬃcile à réconcilier avec
l’existence connue de galaxies et de quasars à z ∼ 5. De plus, la formation précoce
des amas de galaxies mène à des amas plus chauds et plus massifs que ceux que l’on
observe. Nous pouvons conclure que des modèles avec seulement de la matière noire
chaude sont exclus.
L’autre candidat naturel pour de la matière noire non-CDM matière noire est la
matière noire baryonique. Des possibilités seraient des nuages moléculaires froids ou
des étoiles de très faible luminosité. Comme nous l’avons discuté dans la section 4,
les tentatives pour trouver des objets sombres dans le halo de la Voie Lactée n’ont
pas donné des nombres suﬃsants pour rendre compte de la matière noire galactique,
du moins dans la gamme de masse plausible en dessous de ∼ 1 M [85, 84]. Le
gaz moléculaire froid peut être détecté par ses raies d’absorption et aucune n’a été
détectée dans les halos galactiques [89]. Pour échapper à la détection, ce gaz devrait
être contenu dans de petits nuages de façon que la plupart des lignes de visée dans
les halos aient une petite profondeur optique.
Un problème plus fondamental avec la matière noire baryonique provient du comportement des baryons dans l’univers primordial, c’est-à-dire le fait que les baryons
continuent d’interagir fortement avec le gaz de photons relativiste jusqu’à ârec ∼ 10−3 .
Les perturbations de la densité de baryons vont par conséquent continuer d’osciller
comme des ondes acoustiques jusqu’à ce moment, lorsqu’elles peuvent commencer à
s’eﬀondrer pour former des structures. Cela doit être comparé avec les particules de
matière noire froide dont les perturbations commencent à croître librement sur des
échelles sub-Hubble à âeq ∼ 10−4 . Dans le régime linéaire, il s’ensuit que la matière noire froide a un potentiel de croissance 10 fois plus grand que la matière noire
baryonique.
ÉC
E
L
O
T
Y
L
PO
E
L
O
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
4 Les modèles de matière noire chaude sont pour cela appelés modèles « top-down » par opposition
aux modèles matière noire froide appelés « bottom-up » car les plus petites structures se forment
en premier.
ÉC
E
308
E
U
IQ
Chapitre 7. La formation des structures
N
H
EC
Si les ﬂuctuations de densité à l’entrée de Hubble sont ∆H ∼ 2 × 10−5 indépendamment de l’échelle, le facteur 10 en défaveur de la matière noire baryonique rend
diﬃcile la formation des structures observées. Aux échelles galactiques, le problème
est encore pire à cause de « l’amortissement de Silk ». Au moment de la recombinaison, lorsque le libre parcours moyen des photons devient grand, les photons reﬂuent
hors des régions sur-denses. À cause de la diﬀusion Compton résiduelle, ils entraînent
les électrons avec eux et ces derniers entraînent les baryons par attraction coulombienne. Cela détruit les ﬂuctuations sur des échelles galactiques et l’on se retrouve en
face d’un problème semblable à celui de la matière noire chaude. Dans les modèles
de matière noire froide, les ﬂuctuations des baryons sur des échelles galactiques sont
initialement eﬀacées par l’amortissement de Silk mais les baryons retombent alors
dans les puits de potentiel de la matière noire froide.
Le problème de l’amortissement de Silk peut être évité en supposant que les ﬂuctuations primordiales sont des ﬂuctuations d’iso-courbure du rapport baryon/photon.
Dans ce cas, les régions d’excès de baryons ne correspondent pas aux régions d’excès
de photons et l’amortissement de Silk est moins important. Cette solution n’est pas
particulièrement satisfaisante pour au moins deux raisons. D’abord, les ﬂuctuations
d’iso-courbure ne sont pas aussi naturelles que les ﬂuctuations adiabatiques dans les
scénarios inﬂationnaires. Ensuite, nous verrons que le spectre d’anisotropie du CBR
est très naturellement interprété comme provenant de ﬂuctuations adiabatiques invariantes d’échelle. Si les ﬂuctuations primordiales sont d’iso-courbure, il faudrait que
le spectre primordial ait été choisi de façon très habile pour produire le spectre CBR
observé. Bien entendu, si on découvre une quantité suﬃsante de matière noire baryonique pour rendre compte de ΩM , les ﬂuctuations d’iso-courbure primordiales seront
une solution séduisante.
ÉC
E
L
O
ÉC
8
T
Y
L
PO
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
Propagation des photons
Notre seule source d’information sur le spectre primordial des inhomogénéités est
le spectre des anisotropies du CBR. Les inhomogénéités de densité présentes à trec
engendrent des ﬂuctuations de température ∆T /T , c’est-à-dire une température qui
dépend de la ligne de visée.
Pour comprendre les anisotropies, il est d’abord nécessaire de comprendre la propagation des photons dans un univers inhomogène. Pour simpliﬁer le problème, nous
allons considérer un univers à symétrie sphérique introduit en section 1 avec une petite
région sur-dense au centre d’un univers critique. Comme avant, nous allons prendre
comme conditions initiales (7.12) et (7.13). Les paramètres de la métrique (7.8) doivent satisfaire l’équation Friedmannienne (7.9) et la conservation de l’énergie (7.10).
Pour une densité constante, (7.10) devient
E
L
O
Å
ÉC
b
3
Y
L
PO
r ∂b
1+
b ∂r
H
C
TE
U
Q
I
N
ã
= const. ,
(7.132)
E
Propagation des photons
T
Y
L
PO
avec comme solution générale
ÉC
E
L
O
N
H
EC
E
U
IQ
ã
Å
β(t) 1/3
.
b(r, t) = α(t) + 3
r
309
(7.133)
On vériﬁe sans problème que les solutions (au premier ordre en δ1 ) de (7.9) et
(7.10) qui satisfont (7.12), (7.13) et (7.133) sont, pour r > rc
ρ(r > rc , t) = ρ̄(t) = ρ̄(t1 ) ã−3 ,
(7.134)
ï
ò
r3
b(r > rc , t) = a(t) 1 − ã c3 (δ1 /3) ,
r
(7.135)
rc2 a2 rc
(5δ1 /3) ,
d2H r
κ(r > rc )r2 =
et pour r < rc
T
Y
L
PO
N
H
EC
E
U
IQ
ρ(r < rc , t) = ρ̄(t)[1 + ãδ1 ] ,
ÉC
E
L
O
b(r < rc , t) = a(t)[1 − ã(δ1 /3)] ,
κ(r < rc )r2 =
r 2 a2
(5δ1 /3) .
d2H
(7.136)
(7.137)
(7.138)
(7.139)
Comme on s’y attend, les perturbations à la densité, au paramètre d’échelle, et au
paramètre de courbure sont toutes proportionnelles à la perturbation initiale de densité δ1 . Comme on s’y attend aussi, les perturbations à la densité et au paramètre
d’échelle croissent linéairement avec le paramètre d’échelle ã = a/a1 . On voit que κ
est négligeable si la taille rc a de la région sur-dense est négligeable devant dH .
En négligeant la courbure, la métrique radiale pour r > rc est
dτ 2 = dt2 − a(t)2 dr2 (1 − h(r, t)) ,
où
h(r, t) = (4/3) ã
H
C
TE
rc3
M (t)
δ1 =
,
3
r
π ρ̄a3 r3
Y
L
PO
U
Q
I
N
(7.140)
(7.141)
où l’excès de masse dans la région r < rc est
ÉC
E
L
O
M (t) =
4π 3 3
ρ̄a rc ã δ1 .
3
(7.142)
E
310
E
U
IQ
Chapitre 7. La formation des structures
T
Y
L
PO
N
H
EC
Nous pouvons maintenant calculer la propagation des photons en utilisant la métrique (7.140) de la même façon que nous avons calculé la propagation des photons
avec la métrique de Robertson–Walker au chapitre 3. En inversant la conﬁguration
spatiale dans le chapitre 3, nous considérons un photon de longueur d’onde λ1 émis
en r1 > rc et détecté avec une longueur d’onde λ0 en r0 r1 . En traitant le photon comme une onde classique, nous imposons dτ = 0 pour chaque crête d’onde. La
première crête est émise à t1 et détectée à t0 , ce qui implique
r0
t0
dt
=
[1 − (1/2)h(r, t(r))]dr .
(7.143)
t1 a(t)
r1
ÉC
E
L
O
La deuxième crête est émise à t1 + λ1 et détectée à t0 + λ0 :
t0 +λ0
r0 ï
ò
∂h a(t(r))
dt
h(r, t(r))
=
−
λ1
1−
dr .
2
∂t
2a1
t1 +λ1 a(t)
r1
(7.144)
E
U
IQ
Dans cette expression, nous avons fait usage du fait qu’en première approximation la
deuxième crête suit la première avec un intervalle de temps λ1 a(t)/a1 , c’est-à-dire le
délai pour un univers homogène .
Soustrayant (7.143) et (7.143), nous trouvons le redshift :
ñ
ô
r0
∂h
a0
λ0
1 − (1/2)
a(t(r)) dr .
(7.145)
=
z+1 =
λ1
a1
r1 ∂t
ÉC
E
L
O
T
Y
L
PO
N
H
EC
Dans cette expression on voit le redshift pour un univers homogène, a0 /a1 , et la
correction du premier ordre
r0
r0
M (t1 )
∂h
aȧdr
∆λ0
a(t(r)) dr =
= − (1/2)
,
(7.146)
3
λ0
2π ρ̄a a1 r1 r3
r1 ∂t
où nous avons utilisé (7.141).
Pour évaluer cette correction, on peut utiliser la trajectoire non perturbée (δ1 =
0) :
Å ã2/3
t
a1
1/3
a(t) = a1
⇒
t(r)1/3 = t1 + 2/3 (r − r1 ) .
(7.147)
t1
3t
1
Substituant cela dans (7.146), on trouve
∆λ0
GM1
GM1
= (1/3)
+
t1 .
λ0
a1 r1
(a1 r1 )2
T
Y
POL
H
C
E
U
Q
I
N
(7.148)
Les deux termes de cette expression ont une interprétation simple. Le premier est
appelé terme de Sachs–Wolfe (SW) et il est proportionnel au potentiel gravitationnel
du point d’émission
ÉC
E
L
O
(1/3)
GM1
= Φ1 /3 .
a1 r1
(7.149)
E
Propagation des photons
T
Y
L
PO
N
H
EC
E
U
IQ
311
Le facteur 1/3 paraît surprenant car il est absent dans le cas d’un champ gravitationnel
statique (Fig. 3.13). Nous y reviendrons.
Le deuxième terme de (7.148) a aussi une interprétation simple. En utilisant (7.41)
et t1 = (2/3)H1−1 , le deuxième terme est tout simplement la vitesse particulière de la
source projetée sur la direction de l’observateur :
ÉC
E
L
O
GM1
t1 = v1 · n̂ .
(a1 r1 )2
(7.150)
Ce terme est donc nommé le terme de « Doppler ».
Dans un traitement général [162], il n’est pas surprenant que l’on trouve
∆λ0
= (1/3)(Φ1 − Φ0 ) + n̂ · (v1 − v0 ) ,
λ0
où le potentiel gravitationnel au point i est
Φi = Gρ̄a3
N
H
EC
t)d3 r
δ(R,
,
−R
i|
a|R
T
Y
L
PO
(7.151)
E
U
IQ
(7.152)
et où les vitesses particulières sont déterminées par (7.42).
En revenant sur le facteur (1/3) dans le terme de SW, on note que certains préfèrent utiliser un système de coordonnées « newtonien » [158] où le terme de SW est
la somme de deux termes :
ÉC
E
L
O
Φ/3 = Φ − (2/3)Φ .
(7.153)
Le premier terme = Φ1 est le redshift gravitationnel habituel dans un champ gravitationnel statique. Le deuxième terme = −(2/3)Φ1 est dû à ce que dans ces coordonnées,
le temps d’émission diﬀère du temps moyen de Robertson–Walker d’un facteur qui
dépend de la position ∆t/t = Φ. Le redshift cosmologique normal a0 /a1 est ainsi modiﬁé par un facteur −da/a = −(2/3)dt/t où nous avons supposé a ∝ t2/3 . La somme
de ces deux eﬀets donne alors l’eﬀet de SW qui est, bien entendu, le résultat qui a un
sens physique.
On notera également que dans des coordonnées newtoniennes, le contraste de
densité est dominé par le fait que, dans la région dense, l’univers au temps t est
« plus jeune » d’un facteur ∆t/t = Φ et donc plus dense d’un facteur
δ ∼ −2Φ
H
C
E
coordonnées newtoniennes .
T
Y
POL
U
Q
I
N
(7.154)
L’utilisation des coordonnées newtoniennes est devenue populaire dans la discussion
des anisotropies du CBR[160] et nous y reviendrons brièvement dans la section 9.
ÉC
E
L
O
E
312
9
E
U
IQ
Chapitre 7. La formation des structures
N
H
EC
Anisotropies du CBR
T
Y
L
PO
Une fois que l’on a pris en compte dans les corrections la vitesse particulière du
système solaire, 10−3 c, la température du CBR est indépendante des angles d’observation à une précision de ∼ 10−5 . Cette petite dépendance angulaire peut être
caractérisée en développant la température en harmoniques sphériques :
ÉC
E
L
O
T (θ, φ) = (2.725 ± 0.01)Kelvin + (3.358 ± 0.02)mK cos θ
+
alm Ylm (θ, φ) .
(7.155)
l≥2,m
Le deuxième terme (le dipôle) est dû à la vitesse particulière du système solaire. La
direction de cette vitesse donne la direction privilégiée à partir de laquelle on mesure
l’angle polaire θ. La température est réelle, ce qui implique alm ∗ = al−m .
Les termes l > 1 donnent variations de température sur les échelles angulaires ∆θ
avec
LY T
N
H
EC
E
U
IQ
1degré
π
= 200
,
l ∼
∆θ
∆θ
O
P
E
L
ÉCO
(7.156)
où la deuxième forme suit la convention habituelle sur ce qu’on appelle « échelle
angulaire ». Cette connexion angle-multipôle est la conséquence du fait qu’il y a (l−m)
zéros de Ylm pour −1 < cos θ < 1 et m zéros de Re(Ylm ) pour 0 < φ < 2π. L’indice
l peut étre considéré comme l’analogue angulaire de k dans l’analyse de Fourier de
la densité de la section 2. Cette analogie est encore plus claire si l’on considère la
température moyenne T∆θ (θ0 , φ0 ) à l’intérieur d’un petit cercle de diamètre ∆θ autour
de la direction (θ0 , φ0 ). On montre directement (exercice 7.4) que
alm Ylm (θ0 , φ0 )Wl (∆θ) .
(7.157)
T∆θ (θ0 , φ0 ) =
l,m
La fonction Wl (∆θ) (exercice 7.4) tronque la somme pour l > 1/∆θ de la même
façon que la somme correspondante (7.46) pour la densité moyenne dans une sphère
de rayon R était en pratique tronquée pour k > 1/R. Le carré de la température
moyenne près de (θ0 , φ0 ) est
2
(θ0 , φ0 )
T∆θ
=
H
C
TE
alm Ylm (θ0 , φ0 )Wl (∆θ) aij Yij (θ0 , φ0 )Wi (∆θ) .
l,m,i,j
Y
L
PO
En moyennant sur toutes les directions possibles (θ0 , φ0 ) on trouve
1 2
=
|alm |2 |Wl (∆θ)|2 .
T∆θ
4π
ÉC
E
L
O
l,m
U
Q
I
N
(7.158)
(7.159)
E
Anisotropies du CBR
T
Y
L
PO
N
H
EC
E
U
IQ
313
Comme avec les ﬂuctuations de densité, les termes croisés ont disparu à cause de
l’orthonormalité des harmoniques sphériques. Dans cette expression, nous pouvons
remplacer les |alm |2 par leur moyenne sur m
ÉC
E
L
O
Cl = |alm |2 m .
(7.160)
En soustrayant le carré de la température moyenne, on trouve la variance de la température sur l’échelle angulaire ∆θ :
2
∆T∆θ
=
1 (2l + 1) Cl |Wl (∆θ)|2 .
4π
(7.161)
l>0
Pour de petites échelles angulaires, on peut remplacer la somme par une intégrale
∞
dl
1
2
l(l + 1/2) Cl |Wl (∆θ)|2 .
∆T∆θ
=
(7.162)
2π 0 l
N
H
EC
E
U
IQ
On voit que la quantité l(l + 1/2) Cl /2π donne la contribution par intervalle de ln l
aux ﬂuctuations de température de la même façon que ∆2k donne les ﬂuctuations de
masse. Les mesures de la quantité reliée l(l + 1)Cl /2π sont montrées sur la ﬁgure
7.10. Le spectre est relativement plat pour l < 20 avec une valeur de la température
moyenne de ∼ 10−5 . Le fait que le spectre soit plat signiﬁe que les ﬂuctuations de
température (7.162) sont relativement indépendantes de l’échelle angulaire ∆θ pour
∆θ > 10degrés. Nous remarquons également qu’il y a un pic près de l ∼ 200 ce qui
correspond à une échelle angulaire de ∆θ ∼ 1degré.
Il est naturel de penser que les anisotropies du CBR sont dues aux inhomogénéités présentes à trec . Comme l’illustre la ﬁgure 7.11, les anisotropies de température
peuvent être créées par des puits de potentiel, des vitesses particulières, et une variation de température intrinsèque sur la « dernière surface de collision » χ(zrec ).
Les anisotropies sur les échelles angulaires ∆θ sont pour la plupart la projection des
inhomogénéités sur des échelles de distances R (à trec ) données par
ÉC
E
L
O
T
Y
L
PO
∆θ =
R
.
dA (zrec )
(7.163)
La distance angulaire dA (zrec ) a été calculée dans le chapitre 5. Pour un univers avec
ΩΛ = 0, nous avons trouvé
dA (zrec ) =
2H0−1
zrec ΩM
H
C
TE
ΩΛ = 0 .
Y
L
PO
U
Q
I
N
(7.164)
On verra que l’échelle angulaire la plus intéressante est celle de la distance de Hubble
à la recombinaison :
ÉC
E
L
O
dH (arec ) =
H0−1
,
3 )1/2
(ΩM zrec
(7.165)
E
314
E
U
IQ
Chapitre 7. La formation des structures
T
Y
L
PO
N
H
EC
où nous avons utilisé le fait que l’univers était dominé par la matière à trec . Les angles
et le multipole correspondant sont
ÉC
E
L
O
θH =
dH (zrec )
∼ 1 deg ΩT
dA (zrec )
200
lH ∼ √
ΩT
(ΩT = ΩM )
(7.166)
(ΩT = ΩM ) .
(7.167)
Si ΩT ∼ 1, la valeur de θH est assez indépendante des valeurs relatives de ΩΛ et ΩM
(Fig. 5.5).
Dans cette section, nous allons essayer de comprendre le spectre observé et le
spectre prévu par les modèles de matière noire froide. Nous serons particulièrement
intéressés de voir de quelle façon le spectre dépend des paramètres cosmologiques.
Nous verrons que sur de grandes échelle angulaires, ∆θ > θH , les anisotropies dépendent essentiellement du spectre primordial des ﬂuctuations de densité. Sur de petites échelle angulaires, < θH , les anisotropies dépendent de la nature des oscillations
acoustiques du plasma baryons-photons.
9.1
T
Y
L
PO
N
H
EC
E
U
IQ
Les sources d’anisotropies
E
L
O
Chaque direction (θ, φ) correspond à un certain r1 (θ, φ) et t1 (θ, φ) qui donnent la
position et le temps moyens de la dernière interaction entre la matière et les photons
CBR que nous observons à (χ = 0, t0 ). La surface r1 (θ, φ), appelée surface de dernière
diﬀusion est montrée sur la ﬁgure (7.11).
La température dans chaque direction diﬀère de la température moyenne d’une
quantité déterminée par plusieurs eﬀets. Comme nous l’avons vu dans la section 8, les
inhomogénéités de densités engendrent les eﬀets SW et Doppler qui, dans un univers
dominé par la matière, modiﬁent la température comme en (7.151). Cela serait presque
la ﬁn de l’histoire si l’univers devenait transparent à un temps comobile donné trec . En
réalité, la recombinaison se passe à une température preque ﬁxe. Par conséquent, les
régions intrinsèquement chaudes se recombinent plus tard, da1 /a1 = −dT1 /T1 où nous
faisons usage du fait que T ∝ 1/a. Cela modiﬁe le redshift cosmologique normal a0 /a1
d’un facteur da1 /a1 = −dT1 /T1 . La ﬂuctuation observée de la température est alors
dT0 /T0 = −da1 /a1 = dT1 /T1 si bien que les ﬂuctuations de température intrinsèques
à la recombinaison se reﬂètent directement dans les ﬂuctuations observées.
En ajoutant les ﬂuctuations intrinsèques à celles provenant des eﬀets SW et Doppler on a, pour un univers dominé par la matière
ÉC
Y
L
PO
H
C
TE
∆T0
∆T1
(θ, φ) = (1/3)Φ(r1 ) + n̂ · v1 +
.
T0
T1
E
L
O
U
Q
I
N
(7.168)
Nous avons omis le terme proportionnel à Φ(r0 ), qui ne fait qu’ajouter une constante
indépendants des angles, et le terme de dipôle dû à notre vitesse particulière.
ÉC
E
Anisotropies du CBR
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
T
Y
L
PO
E
U
IQ
N
H
EC
315
E
U
IQ
Fig. 7.10: Mesures du spectre des anisotropies du CBR (7.160) en fonction de l’échelle
angulaire (7.156). Les données de grande échelle angulaire (petits l), représentées par des
triangles, proviennent de l’instrument DMR du satellite COBE [159]. Les données de petite
échelle angulaire (grands l) (carrés) sont les données combinées de Boomerang et Maxima
[25]. Les ﬂuctuations de température à grande échelle angulaire sont en gros indépendantes
de l à un niveau de 10−5 de la température du CBR. Le fait que les ﬂuctuations à grand
angle ne dépendent pas de l’échelle constitue une indication que les ﬂuctuations de densité
primordiales sont invariantes d’échelle. Le pic à l ∼ 200 est en général interprété comme
le premier pic acoustique. Sa position indique que ΩT ∼ 1. Les courbes correspondent à des
calculs [164] qui supposent des ﬂuctuations primordiales adiabatiques. La courbe continue est
le meilleur ﬁt qui donne les paramètres (ΩT = 1.2, ΩΛ = 0.5, Ωb h2 = 0.03). La courbe tiretée
est le meilleur ﬁt de ΩT et donne les paramètres (ΩT = 1, ΩΛ = 0.7, Ωb h2 = 0.03). La courbe
pointillée correspond à un univers ouvert avec (ΩT√= 0.3, ΩΛ = 0.0, Ωb h2 = 0.03). Dans
ce modèle, la position du pic est déplacée vers 200/ ΩT ∼ 400. (Avec la permission de K.
Ganga.)
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
316
ÉC
E
U
IQ
Chapitre 7. La formation des structures
E
L
O
T
Y
L
PO
N
H
EC
χ (z rec)
. .. c
.......... ......
.. b.
.. .
.. ... ..
.
. ..
.......... ...... a
.. .
χ=0
d H(a rec ) /10
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
θH
d H(a rec )
Fig. 7.11: Les photons CBR que nous observons proviennent, en moyenne, de la « surface
de dernière diﬀusion » à χ(zrec ). Cette « surface » a de fait une épaisseur d’environ 1/10 de
la distance de Hubble à trec . La distance de Hubble est montrée (pas à l’échelle) et correspond
à un angle ∼ 1 degré dans le ciel si ΩT = 1. Les inhomogénéités de densité sur la surface de
dernière diﬀusion engendrent des anisotropies de température. Les photons de la région dense
a vont être déplacés vers le rouge en remontant de leur puits de potentiel, mais ils auront
une température initiale plus élevée à cause d’une plus grande compression. (Le premier eﬀect
domine à grande échelle.) Les photons provenant de la région sous-dense b seront déplacés
vers le bleu en tombant de leur colline de potentiel, mais ils seront aussi déplacés vers le
rouge puisque le plasma est accéléré vers la région sur-dense derrière la surface de dernière
diﬀusion.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Anisotropies du CBR
T
Y
L
PO
N
H
EC
E
U
IQ
317
Aux trois termes de (7.168), nous devrions ajouter les eﬀets dus aux perturbations
le long de la trajectoire des photons entre la surface de dernière diﬀusion et l’origine.
Le plus intéressant est la diﬀusion Compton sur le gaz ionisé dans les amas de galaxies
(l’eﬀet SZ). Un deuxième eﬀet se manifeste si l’univers n’est pas dominé par la matière
durant tout le temps de vol, c’est-à-dire ΩM = 1. Dans ce cas, on doit refaire le calcul
de la propagation des photons de la section 8 parce que la trajectoire non perturbée
que nous avons utilisée (7.147) n’est plus correcte et parce que le potentiel n’est plus
constant. Ces changements modiﬁent les anisotropies données par (7.168) et (7.148).
Outre les eﬀets qui engendrent des anisotropies, il y a aussi des eﬀets qui les effacent. Le plus important de ceux-ci vient de ce que la recombinaison n’est pas un
événement instantané mais se déroules sur un intervalle de temps ﬁni. Les photons
que nous observons proviennent d’une plage de distances que l’on peut estimer en
résolvant l’équation de Boltzmann pour le plasma photons-baryons à la recombinaison. Le résultat est que l’épaisseur eﬀective de la surface de dernière diﬀusion est
à peu près 1/10 de la distance de Hubble à la recombinaison. La température dans
une direction donnée est par conséquent une moyenne de la température sur cette
échelle. Cela a peu d’eﬀet sur les anisotropies à grande échelle car la température est
moyennée sur des distances encore plus grandes. D’un autre côté, les anisotropies à
petite échelle angulaire sont eﬀectivement moyennées par l’épaisseur de la surface de
dernière diﬀusion. On s’attend donc à peu d’anisotropie sur les échelles inférieures à
1/10 de la distance de Hubble soit environ 0.1 deg pour ΩT = 1. Cela correspond à
des multipôles l > 2000.
Enﬁn, les anisotropies à petite échelle peuvent être eﬀacées si l’univers a été réionisé
suﬃsamment tôt pour créer une profondeur optique non-négligeable entre nous et la
surface de dernière diﬀusion. Cet eﬀet n’est important que si la réionisation s’est
passée avant les redshifts z ∼ 30 (exercice 7.6).
ÉC
E
L
O
ÉC
9.2
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
∆θ > θH
Les anisotropies sur les échelles > θH sont relativement simples à comprendre car,
à trec les inhomogénéités de densités associées sont hors du rayon de Hubble. On peut
donc ignorer la force de rappel de la pression du plasma photons-baryons pendant
que les inhomogénéités évoluent gravitationnellement.
Il est simple d’estimer l’importance relative des trois termes dans (7.168) en fonction de l’échelle angulaire.
Considérons un photon sortant d’une région sur-dense de taille R et de contraste
moyen de densité (∆ρ/ρ)R . Le terme SW (7.149) est d’ordre
H
C
TE
ï
ò
ï
ò
G∆M
∆ρ
∆ρ
4πR3 /3
R2
∆T
∼
∼ Gρ̄
∼
.
T
R
ρ R
R
ρ R d2H
E
L
O
Y
L
PO
U
Q
I
N
(7.169)
Pour un univers dominé par la matière, la dernière expression est indépendante du
temps (δρ/ρ ∝ a, R2 ∝ a2 , et d2H ∝ a3 ). Pour un spectre de ﬂuctuation invariant
d’échelle, δρ/ρ ∝ R−2 et il s’ensuit que δT /T est indépendant de l’échelle. En prenant
ÉC
E
318
E
U
IQ
Chapitre 7. La formation des structures
T
Y
L
PO
N
H
EC
R = dH , on voit que les anisotropies SW donnent directement les ﬂuctuations de
densité à l’entrée du rayon de Hubble :
ÉC
∆T
(SW ) ∼ ∆H
T
E
L
O
∆θ > θH .
(7.170)
Le terme Doppler (7.150) est facile à estimer :
ï
ò
ò
ï
∆ρ
v
4πR3 /3
R
∆ρ
∼ Gρ
t
∼
.
1
c
ρ R
R2
ρ R dH
(7.171)
Cela donne une ﬂuctuation de température qui décroît comme 1/∆θ aux grands
angles :
θH
∆T
(Doppler) ∼ ∆H
T
∆θ
∆θ > θH .
N
H
EC
E
U
IQ
(7.172)
Les ﬂuctuations de température intrinsèques dépendent de la nature des inhomogénéités. Pour des ﬂuctuations adiabatiques, nwimp /nγ est constant. En utilisant nγ ∝ T 3
on trouve
ï ò
δnwimp
δρ
δnγ
∆T
= (1/3)
= (1/3)
,
(7.173)
(intrinsèque) = (1/3)
T
nγ
nwimp
ρ R
c’est-à-dire
ÉC
E
L
O
T
Y
L
PO
∆T
θ2
(intrinsèque) ∼ ∆H H2
T
∆θ
∆θ > θH .
(7.174)
À cause des facteurs diﬀérents de θH /∆θ, l’eﬀet SW domine les anisotropies pour
∆θ θH . Le spectre est indépendant des angles si les inhomogénéités de densité sont
invariantes d’échelle. Si c’est le cas, on s’attend à un spectre plat aux grands angles
qui croît lentement quand l’échelle approche θH et que l’eﬀet Doppler et les eﬀets
intrinsèques deviennent importants. Les observations de la ﬁgure 7.10 indiquent que
c’est le cas. C’est un argument circonstanciel que les ﬂuctuations primordiales sont
adiabatiques et invariantes d’échelle.
9.3
∆θ < θH
H
C
TE
U
Q
I
N
À petite échelle angulaire, les échelles de distance correspondantes sont sub-Hubble
et l’on doit tenir compte la force de rappel de la pression sur le plasma photonsbaryons. Les photons et les baryons demeurent étroitement couplés comme un ﬂuide
parfait jusqu’à la recombinaison. Les équations dynamiques sont un peu compliquées
mais la phénoménologie qui en résulte est simple comme on peut le montrer [160].
Après teq les ﬂuctuations dans la composante de matière noire froide croissent proportionnellement à a(t), comme l’illustre la ﬁgure 7.2. Initialement, le ﬂuide baryonsphotons se comprime dans les puits de potentiel créés par la matière noire froide. La
ÉC
E
L
O
Y
L
PO
E
Anisotropies du CBR
T
Y
L
PO
t
ω(t)dt = π, 3π....
o
ργb
ÉC
E
L
O
N
H
EC
E
U
IQ
319
t
ω(t)dt = π/2, 3π/2...
o
t
o
ω(t)dt = 0, 2π, 4π...
x/a(t)
ρ (a)
Φ cdm (time independent)
N
H
EC
E
U
IQ
Fig. 7.12: Contraste de densité associé à un mode d’oscillation du plasma photons-baryons
avant la recombinaison. Les ﬂuctuations primordiales sont choisies adiabatiques avec un
contraste de densité initial donné par (7.154) en coordonnées newtoniennes.
E
L
O
T
Y
L
PO
compression continue jusqu’à ce que la pression du ﬂuide résiste à une compression
supplémentaire et le ﬂuide se met à se dilater. La dilatation se poursuit alors jusqu’à
ce que la gravitation fasse redémarrer la compression et ainsi de suite.
Les oscillations résultantes sont illustrées sur la ﬁgure 7.12 dans le cas d’un ﬂuctuation primordiale adiabatique5 . La fréquence d’oscillation dépend de la norme du
vecteur d’onde k/â :
ÉC
ωk =
k cs
.
â
(7.175)
La vitesse du son, cs (t), est donnée par (exercice 7.5)
c2s (t) = =
c2
,
3(1 + (t))
où
(t) =
(7.176)
H
C
TE
η
3ρb
a
∼ 0.5
.
4ργ
arec 5 × 10−10
Y
L
PO
U
Q
I
N
(7.177)
√
Dans l’approximation η = 0 on a cs = c/ 3 comme on s’y attend.
E
L
O
5 Les oscillations dues aux ﬂuctuations primordiales d’iso-courbure sont déphasées de π/2 par
rapport à celles dues aux ﬂuctuations adiabatiques car le contraste de densité est ﬁxé à zéro jusqu’à
l’entrée du rayon de Hubble.
ÉC
E
320
E
U
IQ
Chapitre 7. La formation des structures
T
Y
L
PO
N
H
EC
Les oscillations continuent jusqu’à trec lorsque les photons s’échappent librement
des puits de potentiel de matière noire froide. La nature des anisotropies créées par
un mode d’oscillation donné dépend de la phase de l’oscillation à la recombinaison :
ÉC
E
L
O
trec
Θrec (k) =
ωk (t)dt = k a0
0
0
trec
cs (t)dt
.
a(t)
(7.178)
L’intégrale de droite est simplement l’« horizon sonique », c’est-à-dire la coordonnée de longueur de vol√d’un signal sonore entre t = 0 et la recombinaison. Dans
l’approximation cs = 1/ 3
a0 k
a0 k
√ 2dH (arec ) ,
Θrec (k) = √ χhor (arec ) =
3
arec 3
(7.179)
E
U
IQ
où χhor (arec ) est l’horizon (lumineux) à la recombinaison. Pour l’horizon, nous avons
utilisé le fait que l’univers est dominé par la matière à trec ce qui implique que l’horizon
de photon est le double de la distance de Hubble.
La phase Θrec (k) détermine pour chaque mode l’importance relative du redshift
gravitationnel, de l’eﬀet Doppler, et de l’eﬀet de température intrinsèque. On peut
distinguer trois cas extrêmes (voir la ﬁgure 7.12) :
T
Y
L
PO
N
H
EC
– Θrec = nπ, n = 1, 3, 5..... Le ﬂuide est hautement comprimé dans les puits de
potentiel. La température des photons observée est maximale pour des photons
sortant des puits à cause de la haute température intrinsèque dans les puits.
ÉC
E
L
O
– Θrec = nπ, n = 2, 4, 6..... Le ﬂuide est seulement modérément comprimé dans
les puits de potentiel. La température des photons observée est minimale pour
des photons sortant des puits à cause du redshift gravitationnel.
– Θrec = nπ/2, n = 1, 3, 5..... Les eﬀets intrinsèque et de redshift gravitationnel
se compensent. Parce que la vitesse particulière du plasma est maximum dans
cette phase, les variations de température suivent la vitesse du plasma de long
de la ligne de visée.
Alors que l’origine des anisotropies dépend de la phase Θrec (k), ce qui n’est pas
clair d’après cette analyse est de savoir quelles valeurs de k donnent
les plus grandes
√
anisotropies. Il se trouve que dans l’approximation cs = c/ 3, c’est-à-dire η = 0,
l’anisotropie totale obtenue en sommant les trois eﬀets est indépendante de k et par
conséquent indépendante de l’échelle angulaire. Si c’était le cas, le spectre d’anisotropies prévu n’aurait pas de pic du tout. L’addition des baryons au plasma a pour
eﬀet d’ampliﬁer les eﬀets gravitationnels par rapport aux eﬀets Doppler, surtout pour
les modes de compression (n impair). On s’attend donc à des anisotropies renforcées
à des échelles
angulaires correspondant à Θrec (k) = nπ. Dans l’approximation de
√
cs = c/ 3, les échelles de distance favorisées sont les harmoniques de dH (arec )
ÉC
E
L
O
Y
L
PO
H
C
TE
a0 −1
dH (arec )
,
kn ∼
arec
n
U
Q
I
N
(7.180)
E
Anisotropies du CBR
T
Y
L
PO
N
H
EC
E
U
IQ
321
et les échelles angulaires favorisées sont les harmoniques de θH
θn ∼
E
L
O
dH (arec ) 1
.
dA (zrec ) n
(7.181)
On s’attend donc à une série de pics dans le spectre au multipôles associés :
ÉC
l ∼ n lH
n = 1, 2, 3..... .
(7.182)
Comme on le voit sur la ﬁgure 7.10, le premier pic est clairement visible et il y a
l’indication d’un deuxième pic. Les expériences les plus récentes voient clairement le
deuxième et le troisième pics.
9.4
Les paramètres cosmologiques
E
U
IQ
Le spectre des anisotropies du CBR peut être utilisé pour contraindre les valeurs
des paramètres cosmologiques si l’on suppose un modèle pour l’origine des anisotropies. À cause du spectre plat aux grandes échelles angulaires, le modèle le plus naturel
est celui avec des ﬂuctuations primordiales adiabatiques invariantes d’échelle. Les modèles avec des ﬂuctuations primordiales d’iso-courbure ont un eﬀet SW supprimé car
les ﬂuctuations de densité sont nulles hors du rayon de Hubble. Par conséquent, de
tels modèles ne peuvent produire une anisotropie aussi plate qu’en ajustant le spectre
primordial.
La présence du pic le plus important dans le spectre va à l’encontre des modèles
qui engendrent des ﬂuctuations après tentrée au travers d’interactions causales. Une
classe de modèles [163] le fait par la voie de la décroissance de « défauts topologiques ». De tels modèles n’arrivent pas à engendrer la série des pics acoustiques car
la cohérence temporelle entre les diﬀérents modes n’est pas assurée. Dans les modèles
inﬂationnaires, les conditions initiales sont établies dans les tout premiers moments
de l’univers et les modes en décroissance ont depuis longtemps disparu au moment de
trec . Par conséquent, les modes de |k| voisin oscillent avec une phase commune à trec
et des pics acoustiques peuvent être produits.
En supposant que les ﬂuctuations primordiales sont adiabatiques, on peut déduire
l’information suivante sur les paramètres cosmologiques :
– Le spectre primordial.
L’amplitude ∆T /T pour 2 ≤ l < 20 donne l’amplitude des ﬂuctuations de densité à l’entrée du rayon de Hubble à l’échelle de la distance de Hubble actuelle.
Les résultats de COBE impliquent [148, 159]
ÉC
E
L
O
T
Y
L
PO
N
H
EC
H
C
TE
∆H = (2 ± 0.1) × 10−5 .
Y
L
PO
U
Q
I
N
(7.183)
En supposant une forme ∆k ∝ k (3+n)/2 , le ﬁt combiné des données de COBE,
de Boomerang, et de Maxima [25] favorisent une valeur de n proche de la valeur
invariante d’échelle, n = 1 :
ÉC
E
L
O
n = 1.01 ± 0.09 .
(7.184)
E
322
E
U
IQ
Chapitre 7. La formation des structures
T
Y
L
PO
N
H
EC
– ΩT . La position du premier pic acoustique correspond à la distance de Hubble à
trec . Sa valeur est déterminée par ΩM et ΩΛ (ﬁgure 5.5). Si ΩT ∼ 1, la position
du pic est assez insensible aux valeurs relatives de ΩM et ΩΛ . Les données
combinées [25] donnent
ÉC
E
L
O
ΩT = 1.11 ± 0.07 ,
(7.185)
ce qui est compatible avec la prévision inﬂationnaire.
– η ∝ Ωb h2 . La position relative, la hauteur relative et la forme des pics acoustiques dépendent de tous les paramètres qui déterminent la nature des oscillations acoustiques avant la recombinaison et la propagation des photons après recombinaison. Plus important est le rapport baryon/photon η ∝ Ωb h2 qui détermine la vitesse du son (7.176). Comme nous l’avons déjà dit, les pics acoustiques
disparaissent si η = 0 et l’amplitude des pics est très sensible à ce paramètre.
Les résultats les plus récents de Boomerang [25] indiquent
N
H
EC
Ωb h270 = 0.04 ± 0.01 ,
E
U
IQ
(7.186)
en bon accord avec la valeur donnée par la nucléosynthèse.
Comme nous l’avons discuté en section 2, ces données peuvent être combinées avec
les mesures par supernovae de q0 pour déterminer séparément ΩM et ΩΛ . Les résultats
combinés sont [25] :
ÉC
E
L
O
T
Y
L
PO
ΩM ∼ 0.34 ± 0.1
(7.187)
ΩΛ ∼ 0.75 ± 0.1 .
(7.188)
Pour ce qui concerne seulement les anisotropies du CBR, on note que tous les
paramètres cosmologiques aﬀectent, d’une façon ou d’une autre, les détails ﬁns du
spectre[160]. Par exemple, le rapport Ωb /ΩM détermine jusqu’à quel point les oscillations acoustiques se produisent dans les puits de potentiel ﬁxés par la matière noire
froide plutôt qu’elles ne sont déterminées par les baryons eux-mêmes. Les rapports
ΩR /ΩM et ΩΛ /ΩM déterminent la validité de l’approximation de la domination complète de la matière utilisée dans le cacul de la propagation des photons (Sect. 8).
Tous ces rapports peuvent être calculés à partir de la forme précise du spectre. La
connaissance des rapports des Ω, s’ajoutant aux containtes sur (ΩM , ΩΛ ) d’après la
position des pics, détermine la valeur absolue des Ω. L’adjonction de la connaissance
de η ∝ Ωb h2 détermine alors H0 .
Enﬁn, notons que les ondes gravitationnelles primordiales prévues par les modèles
inﬂationnaires engendrent des ﬂuctuations « tensorielles » du CBR. Ces ﬂuctuations
pourraient être observées en mesurant les ﬂuctuations dans la polarisation du CBR.
Les futures mesures de précision [108] du spectre vont donc donner une détermination précise de tous les paramètres cosmologiques si le modèle sous-jacent (matière
noire froide) est correct. Les questions restantes seront « qu’est-ce ? » et « pourquoi
celle-là ? »
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
Exercices sur le chapitre 7
Exercices
T
Y
L
PO
N
H
EC
E
U
IQ
323
7.1 Considérons un univers isotrope avec des coordonnées (t, r, θ, φ) et une métrique
de la forme (7.6).
(a) Montrer que les équations des champs sont [161]
ÉC
E
L
O
β̇ 2 + 2α̇β̇ + e−2β − e−2α [2β + 3(β )2 − 2α β ] = 8πGρ ,
(7.189)
2β̈ + 3β̇ 2 + e−2β − e−2α (β )2 = 0 ,
(7.190)
2β̇ + 2β̇β − 2α̇β = 0 ,
(7.191)
E
U
IQ
où les points et les primes désignent respectivement les dérivées par rapport au temps
t et à r et où
A(r, t) = e2α
(b) Montrer que la solution de (7.191) est
β =
T
Y
L
PO
eα−β
g(r)
E
L
O
N
H
EC
B(r, t) = e2β .
⇒
(7.192)
eα = g(r) eβ β ,
(7.193)
1
(1 − κ(r)r2 )1/2
(7.194)
où g(r) est une fonction arbitraire de r.
(c) En déﬁnissant
ÉC
eβ ≡ rb(r, t)
g(r) ≡
montrer que la métrique prend la forme (7.8).
(d) Avec la notation donnée par (7.194) montrer que (7.189) et (7.190) deviennent
∂ 2 3
∂
[ḃ br + br3 κ(r)] = [(8/3)πGρ] (br3 ) ,
∂r
∂r
2
ḃ2
κ
b̈
+ 2 + 2 = 0.
b
b
b
(e) Montrer que la solution de (7.196) est
ḃ2 b + κb = F (r) ,
Y
L
PO
(7.195)
U
Q
I
N
(7.196)
H
C
TE
(7.197)
où F (r) est une fonction arbitraire de R. Redéﬁnir la coordonnée r et les fonctions b
et κ comme suit
ò1/3
ò
ò
ï
ï
ï
A 2/3
A 1/3
F (r)
κ̃ = κ
,
b̃ = a
r̃ = r
A
F (r)
F (r)
ÉC
E
L
O
E
324
E
U
IQ
Chapitre 7. La formation des structures
T
Y
L
PO
N
H
EC
où A est une constante. Montrer qu’avec cette transformation, (7.195) et (7.196)
deviennent (7.9) et (7.10).
E
L
O
7.2 Diviser (7.17) par (7.15) pour trouver une équation pour dãc /dã. Montrer que,
dans le cas Ω1 = 1, la solution de l’équation est
ÉC
ãc = ã (1 − ã) ,
(7.198)
et déterminer la constante . Utiliser (7.38) pour démontrer que le contraste de densité
croît linéairement pendant l’époque de matière.
7.3 Considérons un référentiel dans lequel le CBR a une distribution dans l’espace
des phases isotrope et planckienne :
F (px , py , pz ) = F (E) =
1
1
.
(2π)3 exp(E/T ) − 1
N
H
EC
E
U
IQ
(7.199)
Considérons un deuxième référentiel (primé) relié au premier par une transformation
de Lorentz propre le long de la direction z avec β 1. Considérons les dN photons
= (0, 0, 0) de volume
qui dans le référentiel original sont, à t = 0, dans un cube en R
dxdydz et dans un cube de l’espace des impulsions en p = (px , py , pz ) de volume
dpx dpy dpz . En faisant une transformation de Lorentz transformations à l’ordre β,
montrer qu’à t = 0 les dN photons sont dans le volume représenté sur la ﬁgure 7.13.
Montrer que dans l’espace des impulsions les particules sont dans un espace de volume
(1 + vz β)dpx dpy dpz . Conclure que la densité dans l’espace des phases est la même
dans les deux référentiels avec
ÉC
E
L
O
T
Y
L
PO
F (px , py , pz ) = F (E (1 − β cos θ )) ,
(7.200)
où θ = cos−1 (pz /p ) est l’angle du photon vu dans le référentiel primé. Cette distribution correspond à une distribution Planckienne avec une température qui dépend
de l’angle :
T (θ ) = T (1 − β cos θ ) .
7.4 Pour démontrer (7.157) nous commençons par
1
dΩ
T∆θ (θ0 , φ0 ) =
alm Ylm (θ, φ) ,
∆Ω
l,m
Y
L
PO
H
C
TE
(7.201)
U
Q
I
N
(7.202)
où l’intégrale est sur l’angle solide ∆Ω = π∆θ2 à l’intérieur du cercle de rayon ∆θ
centré sur (θ0 , φ0 ). Il est commode d’exprimer les Ylm (θ, φ) en fonction des Ylm (θ , φ )
où θ , φ sont les angles polaires par rapport à la direction (θ0 , φ0 ) :
m
Dlm
Ylm (θ , φ ) .
(7.203)
Ylm (θ, φ) =
ÉC
E
L
O
m
E
Exercices sur le chapitre 7
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
325
z
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
dz(1−vz β)
x
dy
dx
y
U
Q
I
N
Fig. 7.13: Les photons qui, dans le système non-primé, sont dans un cube de volume dxdydz
en x = y = z = t = 0 sont, dans le système primé, dans le paralléllépipède montré sur la
ﬁgure à t = 0.
ÉC
E
L
O
Y
L
PO
H
C
TE
E
326
E
U
IQ
Chapitre 7. La formation des structures
T
Y
L
PO
N
H
EC
Utiliser la relation (bien connue en mécanique quantique)
…
4π
0
Ylm (θ0 , φ0 ) ,
Dlm
=
2l + 1
E
L
O
pour montrer que
ÉC
T∆θ (θ0 , φ0 ) =
(7.204)
alm Ylm (θ0 , φ0 ) Wl (∆θ) ,
(7.205)
l,m
où
Wl (∆θ) =
2
∆θ2
1
Pl (cos θ)d cos θ ,
(7.206)
cos ∆θ
E
U
IQ
où Pl est un polynôme de Legendre. Parmi les propriétés bien connues des Pl il y a
T
Y
L
PO
d’où il découle que, comme on s’y attendait,
l(l + 1)
,
2
N
H
EC
Pl (1) =
Pl (1) = 1
Wl (l ∆θ−1 ) = 1 .
E
L
O
(7.207)
(7.208)
Pour l 1/∆θ l’intégrand oscille dans l’intervalle d’intégration et Wl (∆θ 1/l) → 0.
Pour quantiﬁer cela, nous utilisons une autre propriété des Pl :
1
1
sin2 θPl (cos θ) ,
Pl (cos θ)d cos θ =
(7.209)
l(l
+
1)
cos ∆θ
ÉC
d’où il résulte que
Wl (∆θ) =
2
P (cos θ) .
l(l + 1) l
(7.210)
Pour l grand, Pl est une fonction oscillante de période ∝ l−1 et d’enveloppe ∝ l−1/2
d’où il découle que Pl est une fonction oscillante d’enveloppe ∝ l 1/2 . Nous en concluons
que
Wl (l ∆θ−1 ) ∝ l−3/2 .
H
C
TE
U
Q
I
N
(7.211)
Cette chute à grand l est suﬃsante pour garantir que la ﬂuctuation de température
sur l’échelle ∆θ (7.162) converge pour Cl indépendamment de l.
Y
L
PO
7.5 Considérons un volume V contenant un gaz à deux composantes de photons
et de baryons non-relativistes avec pγ = ργ /3 et pb ∼ 0. Si le volume est comprimé
adiabatiquement, on a d(ρV ) = −pdV . Montrer que la vitesse du son (7.66) est donnée
par(7.176).
ÉC
E
L
O
E
Exercices sur le chapitre 7
T
Y
L
PO
N
H
EC
E
U
IQ
327
7.6 Supposons que l’univers a été réionisé à ari . Calculer, en fonction de ari , la probabilité qu’un photon CBR subisse une diﬀusion Compton sur la matière réionisée.
Pour quel ari la profondeur optique est-elle plus grande que 1 ?
Discuter le fait que si la profondeur optique est de l’ordre de 1, les anisotropies
du CBR sont détruites sur des échelles angulaires inférieures à θH (ari ) et calculer cet
angle.
ÉC
E
L
O
contenue dans une sphère de rayon R centrée en
7.7 Considérons la masse MR (R)
R. Les ﬂuctuations locales de la masse peuvent s’estimer en la comparant à la masse
moyenne autour de la sphère, par exemple
− (1/8)M2R (R)
.
δMR = MR (R)
(7.212)
E
U
IQ
Calculer la variance δMR2 et montrer qu’elle ne dépend que de la fonction ∆k pour
les valeurs de ln k proches de ln(1/R).
N
H
EC
7.8 Quelle est la longueur actuelle du plus grand mode qui ne soit jamais sorti du
rayon de Hubble pendant l’époque du rayonnement ? C’est le plus grand mode qui ne
devrait pas avoir un spectre à peu près invariant d’échelle.
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
ÉC
N
H
EC
T
Y
L
PO
E
L
O
E
U
IQ
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
E
T
Y
L
PO
N
H
EC
E
U
IQ
E
L
CO A
ÉAnnexe
Vecteurs et tenseurs de
Lorentz
N
H
EC
E
U
IQ
Considérons un système de coordonnées x̃µ , µ = 0, 1, 2, 3 et un autre système de
coordonnées x(x̃). La diﬀérentielle dxµ est donné par la règle
ÉC
E
L
O
T
Y
L
PO
dxµ =
∂xµ α
dx̃ .
∂ x̃α
(1.1)
Tout objet se transformant comme dxµ est appelé « quadrivecteur contravariant »,
c’est-à-dire
Vµ =
∂xµ α
Ṽ ,
∂ x̃α
(1.2)
où Ṽ est le vecteur dans le système x̃ et V celui dans le système x. Les meilleurs
exemples de vecteurs contravariants sont la quadri-vitesse v µ = dxµ /dτ , et la quadriimpulsion pµ = mv µ . Ce sont manifestement des quadrivecteurs contravariants car
dxµ est un quadri-vecteur contravariant et dτ est invariant (il est déﬁni par une
horloge dans son système au repos).
Une deuxième espèce de vecteur apparaît naturellement lorsque l’on considère le
quadri-gradient d’un fonction scalaire (invariante de Lorentz) φ. Cet objet se transforme selon
∂φ
∂ x̃α ∂φ
=
.
µ
∂x
∂xµ ∂ x̃α
Y
L
PO
H
C
TE
U
Q
I
N
(1.3)
Tout objet qui se transforme comme un quadri-gradient est appelé « quadrivecteur
covariant », c’est-à-dire
ÉC
E
L
O
Uµ =
∂ x̃α
Ũα .
∂xµ
329
(1.4)
E
330
E
U
IQ
Annexe A. Vecteurs et tenseurs de Lorentz
T
Y
L
PO
N
H
EC
Les tenseurs sont des généralisations des vecteurs. Par exemple, un tenseur contravariant de rang 2, T µν , se transforme comme
ÉC
E
L
O
T µν =
∂xµ ∂xν αβ
T̃ ,
∂ x̃α ∂ x̃β
(1.5)
tandis qu’un tenseur covariant de rang 2, Tµν , se transforme comme
Tµν =
∂ x̃α ∂ x̃β
Ũαβ .
∂xµ ∂xν
(1.6)
Le tenseur énergie-impulsion d’un système de particules (4.30) est un exemple de
tenseur contravariant. D’un autre côté le tenseur énergie-impulsion d’un champ scalaire s’écrit naturellement comme un tenseur covariant (4.70). Puisque nous voudrons
utiliser les deux dans la même équation de équation de Friedmann, il nous faut savoir transformer les tenseurs covariants en tenseurs contravariant. Nous le ferons cidessous.
Dans ce livre, nous nous intéressons surtout aux transformations de Lorentz et
nous nous penchons plus particulièrement sur cette classe simple de transformations. Comme nous le montrons dans l’exercice 3.1, les coeﬃcients de transformation
∂ x̃α /∂xµ des « boosts » de Lorentz et des rotations sont constants et satisfont
ÉC
E
L
O
T
Y
L
PO
ηκλ
N
H
EC
E
U
IQ
∂xκ ∂xλ
= ηαβ .
∂ x̃α ∂ x̃β
(1.7)
En comparant avec (1.6) on voit que ηµν est un tenseur invariant de rang 2. Il est facile
de montrer que η µν = ηµν est un tenseur contravariant de rang 2 qui est invariant :
η αβ
∂xκ ∂xλ
= η κλ .
∂ x̃α ∂ x̃β
(1.8)
On peut changer le rang d’un tenseur par contraction. Par exemple, il est facile de
voir que la quadri-divergence d’un vecteur de Lorentz, ∂V µ /∂xµ , est un invariant de
Lorentz. De même, la quadri-divergence d’un tenseur de Lorentz, ∂T µν /∂xµ = V ν ,
est un vecteur de Lorentz. Une quantité ayant une quadri-divergence nulle donne une
loi de conservation locale invariante de Lorentz, par exemple
∂j 0
∂j µ
· j = 0 ,
− ∇
=
µ
∂x
∂t
H
C
TE
U
Q
I
N
(1.9)
ce qui signiﬁe que la dérivée temporelle de la « densité » (j 0 ) est égale à la divergence
du « courant » (j). S’il existe une surface fermée sur laquelle le courant s’annule, la
« charge » totale à l’intérieur de la surface est conservée :
d
j 0 dV = 0 .
(1.10)
dt
ÉC
E
L
O
Y
L
PO
E
T
Y
L
PO
N
H
EC
E
U
IQ
331
Montrons maintenant que l’on peut transformer un quadrivecteur contravariant
en un quadrivecteur covariant par l’opération simple
E
L
O
Ṽµ = ηµν Ṽ ν
Vµ = ηµν V ν .
(1.11)
Pour vériﬁer que les objets obtenus par cette opération sont eﬀectivement des quadrivecteurs covariants, faisons une transformation du système x̃ :
ÉC
∂ x̃α
∂xκ ∂xλ β
∂ x̃α
∂ x̃α
Ṽα =
Ṽ ,
ηαβ Ṽ β =
ηκλ α
ν
ν
ν
∂x
∂x
∂x
∂ x̃ ∂ x̃β
(1.12)
où dans la deuxième forme nous avons utilisé (1.7). Le premier et le troisième facteur
à droite se combinent pour donner un δ de Kronecker
∂xκ
∂ x̃α ∂xκ
=
= δνκ ,
ν
α
∂x ∂ x̃
∂xν
et l’on trouve
N
H
EC
∂ x̃α
∂xλ β
Ṽ
Ṽ = ηνλ V λ = Vν .
=
η
α
νλ
∂xν
∂ x̃β
T
Y
L
PO
E
U
IQ
(1.13)
(1.14)
En comparant l’extrême droite et l’extrême gauche, on voit que Vν déﬁni par (1.11)
est eﬀectivement un quadrivecteur covariant. L’équation (1.11) peut se généraliser à
des tenseurs de façon évidente, par exemple
ÉC
E
L
O
ÉC
Vµν = ηµα ηνβ V αβ .
E
L
O
Y
L
PO
(1.15)
H
C
TE
U
Q
I
N
E
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
ÉC
N
H
EC
T
Y
L
PO
E
L
O
E
U
IQ
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
E
T
Y
L
PO
N
H
EC
E
U
IQ
E
L
CO B
ÉAnnexe
Unités naturelles
E
U
IQ
Dans ce livre, nous utilisons sonvent des « unités naturelles » ce qui veut dire que
dans les formules nous omettons les facteurs , c et k. C’est une convention essentiellement destinée à faire des économies d’encre car de tels facteurs ne contiennent
aucune information. Considérons deux quantités A et B, de dimension
T
Y
L
PO
N
H
EC
[A] = longueurl massem tempsn .
ÉC
E
L
O
[B] = longueurλ masseµ tempsν .
(2.1)
(2.2)
On peut, de façon générale, trouver un système d’exposants unique x, y et z tels
que l’équation suivante est correcte sur le plan dimensionnel
A = cx y B z ,
(2.3)
où x, y et z sont les solutions des équations :
l = x + 2y + λz
m = y + µz
n = −x − y + νz .
(2.4)
Puisque les exposants sont uniques, on peut omettre les facteurs c et et écrire (2.3)
comme
A = Bz .
H
C
TE
U
Q
I
N
(2.5)
Si l’on a utilisé la bonne valeur de z dans cette formule, x et y peuvent être trouvés
simplement par analyse dimensionnelle et l’équation « dimensionellement correcte »
(2.3) s’ensuit.
On peut évidemment généraliser ce procédé à des formules qui comportent des
sommes de termes. La dimension de température peut également être incorporée
puisque les températures peuvent être converties en énergies en multipliant par la
constante de Boltzmann k.
ÉC
E
L
O
Y
L
PO
333
E
334
E
U
IQ
Annexe B. Unités naturelles
T
Y
L
PO
N
H
EC
L’utilisation la plus fréquente des unités naturelles dans ce livre concerne des
expressions relativistes où l’on omet les facteurs c, par exemple
dτ 2 = dt2 − dx2
ÉC
et
E
L
O
→
dτ 2 = dt2 − dx2 c−2 ,
(2.6)
E 2 = p 2 c2 + m 2 c4
(2.7)
dH = cH0−1 .
(2.8)
→
E 2 = p 2 + m2
dH = H0−1
→
Les quantités « sans dimensions » sont particulièrement intéressantes, par exemple
les vitesses
v
∼ 10−3
v ∼ 10−3
→
(2.9)
c
et les potentiels gravitationnels
Φg ∼ 10−6
N
H
EC
Φg
∼ 10−6 .
c2
→
T
Y
L
PO
E
U
IQ
(2.10)
Dans les formules quantiques, on manipule des quantités qui sont des puissances
d’une énergie (ou d’une température). Les énergies, les masses et les impulsions ont
clairement z = 1 comme dans (2.7). Plus intéressant est le fait que les longueurs et
les temps ont z = −1, par exemple
ÉC
E
L
O
λ =
2π
Eγ
→
λ =
→
ω = Eγ
2πc
Eγ
(2.11)
ω = Eγ / .
(2.12)
Le fait que les longueurs ont z = −1 signiﬁe que les sections eﬃcaces ont z = −2
σT =
8π 2 −2
α me
3
→
σT =
8π 2
α (me c2 )−2 (c)2 .
3
De même, les densités de particules ont z = 3 :
n =
2.4 3
T
π2
→
Å
mT
n = 2
2π
E
L
O
Å
→
ÉC
n =
ã3/2
1
2.4
(kT )3
π2
(c)3
Y
L
PO
mc2 kT
n = 2
2π
H
C
TE
(2.13)
U
Q
I
N
(2.14)
exp(−m/T )
ã3/2
exp(−mc2 /kT )
1
.
(c)3
(2.15)
E
T
Y
L
PO
N
H
EC
E
U
IQ
335
Notons que dans cette dernière formule, non-relativiste, les facteurs c s’éliminent
comme prévu.
Les densités d’énergie ont z = 4
ÉC
E
L
O
ρ =
2π 2 4
T
30
→
ρ =
1
2π 2
(kT )4
.
30
(c)3
(2.16)
Enﬁn, l’équation de Friedmann a z = 2
H2 =
8π 3 T 4
45 mpl 2
→
H2 =
8πGρ
,
3
(2.17)
où la masse de Planck mpl est déﬁnie par mpl = (c/G)1/2 .
G =
ÉC
E
L
O
ÉC
1
mpl 2
→
G =
T
Y
L
PO
E
L
O
c
.
mpl 2
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
(2.18)
U
Q
I
N
E
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
ÉC
N
H
EC
T
Y
L
PO
E
L
O
E
U
IQ
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
E
T
Y
L
PO
N
H
EC
E
U
IQ
E
L
CO C
ÉAnnexe
Particules élémentaires
E
U
IQ
Les particules connues dont la liste est dans la table 6.2 peuvent subir entre elles des
collisions élastiques ou inélastiques. L’ensemble des règles qui permettent de calculer
les taux de réactions constituent ce qu’on appelle le « modèle standard de la physique
des particules » [9, 10, 11, 12, 21]. Dans ce modèle, la plupart des réactions permises
peuvent être construites à partir de processus élémentaires à trois particules de la
forme
et
ÉC
E
L
O
T
Y
L
PO
N
H
EC
fermion + boson ↔ fermion
(3.1)
fermion + antifermion ↔ boson .
(3.2)
(Il existe aussi des réactions à trois particules de la forme (boson + boson ↔ boson)
mais elles ne sont pas importantes pour les réactions considérées ici.) Les seules réactions à trois particules permises sont celles qui conservent la charge électrique, et,
dans le cas d’interactions quarks-gluons, la « couleur ». Des exemples de réactions
assemblées sont montrés sur les ﬁgures C.1 et C.2.
Le Modèle standard est une théorie quantique des champs qui fournit les règles
qui transforment chaque dessin des ﬁgures C.1 et C.2 en des amplitudes. Le taux
d’une réaction donnée s’obtient en sommant sur toutes les amplitudes pour les mêmes
particules initiales et ﬁanles et en élevant au carré. Lorsque le « boson de Higgs »,
qui n’a pas été encore découvert, viendra s’ajouter aux particules déjà connues, le
modèle standard donnera des taux bien déﬁnis pour tous les processus physiques, ce
qui veut dire notamment que la théorie est renormalisable.
Parmi d’autres choses, à chaque « vertex » d’une réaction à trois particules fondamentale est associée une constante de couplage qui donne l’intensité de l’interaction.
Dans le modèle standard, toutes les constantes de couplage sont, à un ordre de grandeur près, égales à la valeur absolue de la charge électrique. Un diagramme comportant
n vertex donne par conséquent une amplitude d’ordre αn .
ÉC
E
L
O
Y
L
PO
337
H
C
TE
U
Q
I
N
E
338
E
U
IQ
Annexe C. Particules élémentaires
T
Y
L
PO
N
H
EC
Lorsque, dans le calcul de sections eﬃcaces, on somme les amplitudes, les constantes
de couplage eﬀectives varient avec l’énergie. On s’attend à ce que toutes les constantes
de couplage deviennent égales à l’échelle d’énergie de « Grande Uniﬁcation », que
l’on estime être de l’ordre de 1015 à 1016 GeV. On pense qu’une théorie plus complète,
faisant intervenir des particules lourdes, se manifestera à ces énergies. Les eﬀets de
gravitation quantique devraient devenir importants à l’échelle de Planck ∼ 1019 GeV.
ÉC
E
L
O
Au dessous de la température de déconﬁnement, de l’odre de ∼ 400 MeV, les
quarks et les gluons interagissent d’une façon qui les conﬁne dans des hadrons. Les
baryons, par exemple les protons et les neutrons, sont des états liés de trois quarks et
de gluons alors que les mésons, par exemple π ± , π 0 , sont des états liés de quarks et
d’antiquarks. Au dessus de la température de déconﬁnement, on pense que les quarks
et les gluons sont libres et se comportent comme des particules ordinaires.
La plupart des réactions intéressantes du point de vue cosmologique font intervenir
les interactions « électrofaibles » dont les bosons médiateurs des réactions fondamentales à trois particules sont γ, Z 0 ou W ± . Les interactions fondamentales à trois
particules sont de deux types, des « interactions de courants neutres » où le boson
est γ ou Z 0 et des « interactions de courants chargés » où le boson est W ± . Les
réactions dues à l’échange des bosons W ou Z sont appelées interactions « faibles »
car dans la limite des basses énergies les amplitudes sont inversement proportionnelles
au carré de la masse des bosons lourds et sont donc « petites ».
Les réactions de courants neutres apparaissent principalement dans la diﬀusion
élastique, dans l’annihilation particule-antiparticule et dans les désintégrations. Dans
le modèle standard, elles obéissent toutes à la règle que les deux fermions doivent être
identiques, c’est-à-dire
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
e− Z 0 ↔ e−
mais pas
e− Z 0 ↔ µ− ,
(3.3)
e+ e− ↔ Z 0
mais pas
e+ µ− ↔ Z 0 .
(3.4)
Les réactions de courants chargés changent les fermions en d’autres types de fermions par exemple :
νe W − ↔ e−
et
uW − ↔ d .
(3.5)
U
Q
I
N
Les réactions de courants chargés peuvent également annihiler des fermions avec des
antifermions :
νe e+ ↔ W +
H
C
TE
ud̄ ↔ W + .
Y
L
PO
et
(3.6)
Parce que les bosons W ± ont une charge entière, il n’existe pas de réaction qui
transforme un lepton en un quark.
Les diagrammes d’annihilation de paires électron-positron pairs et de neutrinos
sont représentés sur la ﬁgure C.1.
ÉC
E
L
O
E
ÉC
E
L
O
T
Y
L
PO
N
H
EC
e+
E
U
IQ
339
γ
e
e−
γ
νe νµ ντ
ÉC
E
L
O
T
Y
L
PO
N
H
EC
e+
E
U
IQ
Z
e−
ν−e ν−µ ν−τ
e−
νe
W
−
νe
e+
U
Q
I
N
Fig. C.1 : Diagrammes des réactions e+ e− → γγ, νe ν̄e → e+ e− , et νµ ν̄µ → e+ e− .
ÉC
E
L
O
Y
L
PO
H
C
TE
E
340
ÉC
E
U
IQ
Annexe C. Particules élémentaires
E
L
O
T
Y
L
PO
N
H
EC
_
νe
e
W
u
d
u
d
ÉC
E
d
L
O u
T
Y
L
PO
N
H
EC
d
u
d
E
U
IQ
d
u
u
W
_
e
_
νe
U
Q
I
N
Fig. C.2 : Diagrammes des réactions νe n → e− p et n → pe− ν̄e .
ÉC
E
L
O
Y
L
PO
H
C
TE
E
T
Y
L
PO
N
H
EC
E
U
IQ
341
Les réactions des neutrons et des protons peuvent se traiter en incorporant des
quarks « spectateurs » dans le diagramme. Des exemples en sont montrés sur la ﬁgure
C.2.
Les règles qui permettent de transformer les diagrammes en amplitudes se trouvent
dans tous les traités habituels [9, 10, 11, 12]. En plus des constantes de couplage pour
chaque vertex, une amplitude contient des facteurs cinématiques que détermine la
théorie quantique des champs. Par exemple, dans les interactions de neutrinos de
basse énergie importantes en cosmologie à T ∼ MeV, la présence des bosons W ± et
−2
Z 0 donnent des facteurs m−2
W ∼ mZ dans les amplitudes. En combinant ces facteurs
avec les constantes de couplage, on obtient des carrés d’amplitudes de l’ordre de
α2 /m4W ∼ G2F où GF est la constante de Fermi. Les sections eﬃcaces et les taux de
désintégration s’obtiennent en multipliant par des facteurs reliés au volume total de
l’espace des phases des particules de l’état ﬁnal. La forme de ces facteurs, et son ordre
de grandeur, peut souvent se deviner par analyse dimensionnelle. Les sections eﬃcaces
ont la dimension d’une énergie−2 , par conséquent G2F doit être multiplié par le carré
d’une énergie. La section eﬃcace d’annihilation νe ν̄e par exemple est
ò
2 ï
G2F Ecm
1
2
4
σ =
+ 2 sin θW + 4 sin θW ,
(3.7)
12π
2
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
alors que celle des réactions d’annihilation νµ ν̄µ et ντ ν̄τ est
ï
ò
1
G2 E 2
− 2 sin2 θW + 4 sin4 θW .
σ = F cm
12π
2
ÉC
E
L
O
(3.8)
Dans ces deux expressions, sin2 θW ∼ 0.23 est l’un des paramètres du modèle standard
(θW est appelé angle de Weinberg).
Dans le domaine me Eν mp la section eﬃcace de la réaction νe n → e− p est
σ =
Å
ã2
G2F Eν2 Eν
2
1 + 3gA
cos2 θc ∼ 9 × 1041
cm2 ,
π
10 MeV
(3.9)
où cos2 θc ∼ 0.98 et gA ∼ 1.2. Les taux de désintégration ont la dimension d’une
énergie et G2F doit être multiplié par la cinquième puissance d’une énergie. Le taux
de désintégration du neutron, par exemple, est
τn−1 ∼ G2F Q5 ,
U
Q
I
N
(3.10)
H
C
TE
où Q = mn − mp − me est l’énergie libérée dans la désintégration.
Les extensions supersymétriques du modèle standard sont intéressante du point
de vue cosmologique car elles procurent des candidats pour la matière noire nonbaryonique de façon naturelle. Dans ces théories, chaque fermion (boson) de la table
6.2 est apparié avec un partenaire lourd, jusqu’ici non identiﬁé expérimentalement,
qui est un boson (fermion). Le photon γ, de spin 1, par exemple, est apparié avec
un « photino » lourd γ̃ de spin 1/2. Chaque quark de spin 1/2, q est apparié à un
« squark » q̃ lourd de spin 0 .
ÉC
E
L
O
Y
L
PO
E
342
~
γ
ÉC
E
U
IQ
Annexe C. Particules élémentaires
E
L
O
PO
LY T
N
H
EC
q
q~
~
γ
−q
~
γ
q
q~
~γ
q
T
Y
L
PO
N
H
EC
E
U
IQ
Fig. C.3: Diagrammes des réactions γ̃γ̃ → qq̄ et γ̃q → γ̃q. Le premier contribue à l’annihilation des photinos, ce qui détermine l’abondance du reliquat de photinos. Le second
détermine la section eﬃcace de collision élastique des photinos sur les noyaux.
ÉC
E
L
O
Les interactions des particules supersymétriques s’obtiennent en prenant les interactions fondamentales à trois particules des particules habituelles et en changeant
deux des particules dans leurs partenaires supersymétriques. Par exemple :
e− γ ↔ e−
→
e− γ̃ ↔ ẽ− ,
(3.11)
où ẽ est le « sélectron ».
Les diagrammes d’annihilation de photinos en quarks et ceux de la diﬀusion de
photinos sur les quarks sont dessinés sur la ﬁgure C.3.
La particule supersymétrique la plus légère (LSP), appelée de façon générique χ,
devrait être une combinaison linéaire des photinos, du Zino (partenaire du Z 0 ) et des
higgsinos (partenaires des bosons de Higgs). L’abondance du reliquat de cette particules est déterminée par sa section eﬃcace d’annihilation cross-section (section 6).
Comme pour les neutrinos, la section eﬃcace d’annihilation contient un facteur α2 ,
un facteur m−4 pour la particule échangée et un facteur cinématique qui se trouve
être m2χ
Y
L
PO
α2 2
σ(v/c) ∼
m .
mẽ4 χ
E
L
O
H
C
TE
U
Q
I
N
(3.12)
Pour une valeur donnée de mχ il est donc possible de trouver une valeur appropriée de
mẽ telle que la section eﬃcace d’annihilation soit du bon ordre de grandeur (σv/c ∼
10−37 cm2 , voir section 6) pour fournir la matière noire cosmologique.
ÉC
E
T
Y
L
PO
N
H
EC
E
U
IQ
E
L
CO D
ÉAnnexe
Magnitudes
N
H
EC
E
U
IQ
À cause de la grande diversité des luminosités stellaires et galactiques, les astronomes expriment en général ces luminosités sur une échelle logarithmique de « magnitude absolue ». Pour un objet de luminosité totale L, la magnitude bolométrique
absolue est déﬁnie par
T
Y
L
PO
Mbol ≡ −2.5 log(L/L ) + 4.76 ,
E
L
O
(4.1)
où L est la luminosité du Soleil et 4.76 sa magnitude. On notera qu’en raison du
signe moins, les étoiles brillantes ont de petites magnitudes. Le choix du facteur 2.5
peut sembler étrange mais il a la propriété de donner des expressions simples à la fois
pour les diﬀérences de luminosité grandes (5 magnitudes correspondent à un facteur
100 en luminosité) ou faibles (∆L/L ∼ ∆M ).
Il est très diﬃcile de mesurer des magnitudes bolométriques et les astronomes
observent en général au travers d’un ﬁltre qui sélectionne une bande spectrale, ou
« couleur » particulière. Les ﬁltres les plus utilisés sont décrits dans la table D.1.
Pour un objet de luminosité LC dans la bande C, la magnitude absolue MC est
déﬁnie par
ÉC
MC ≡ −2.5 log(LC /LC) + MC
C = U, B, V, R, I......
(4.2)
U
Q
I
N
La diﬀérence entre deux magnitudes, par exemple MB − MV , est l’« indice de
couleur » d’un objet. Par convention, un indice de couleur est toujours la magnitude
de la longueur d’onde la plus courte moins celle de la plus longue. En raison de l’échelle
logarothmique, une étoile bleue (chaude) a de faibles indices de couleur.
Comme pour les luminosités, les astronomes expriment en général les ﬂux sur une
échelle logarithmique de « magnitude apparente ». Pour une étoile de ﬂux φC (hors
de l’atmosphère terrestre) dans la bande C, la magnitude apparente mC est déﬁnie
par
ÉC
E
L
O
Y
L
PO
mC ≡ C = −2.5 log φC + αC
343
H
C
TE
C = U, B, V, R, I
E
344
ÉC
E
U
IQ
Annexe D. Magnitudes
E
L
O
T
Y
L
PO
N
H
EC
Tab. D.1: Filtres habituels dans le système UBVRI utilisé dans les observations au
sol [2]. Mis à part certaines bandes infrarouges, les longueurs d’onde entre le domaine
radio (λ ∼ 1 cm) et le proche infrarouge (λ ∼ 1000 nm) sont fortement absorbées par
l’atmosphère et les observations sont faites en avion, en ballon ou en satellite. Les
observations par satellite sont également nécessaire pour les longueurs d’onde courtes
entre λ ∼ 300 nm et celles des photons d’une énergie du TeV. La dernière colonne
donne l’absorption galactique interstellaire de la bande (coeﬃcient d’extinction) par
rapport à celle de la bande V.
λ
(nm)
∆λ
(FWHM)
Mλ
(Soleil)
AC /AV
U (ultraviolet)
365
66
5.61
1.531
B (bleu)
445
94
5.48
1.324
V (visible)
551
88
4.64
1.0
R (rouge)
658
138
4.42
0.748
I (infrarouge)
806
149
4.08
0.482
J
1200
213
3.64
0.282
K
2190
390
3.28
0.112
∞
4.76
ﬁlter
ÉC
N
H
EC
E
U
IQ
E
L
O
T
Y
L
PO
bolométrique
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
N
H
EC
E
U
IQ
345
où αC est une constante. En l’absence d’absorption interstellaire, on a φC = LC /(4πR2 )
où R est la distance de l’étoile. Cela implique que m = M + 5 log R + constant. La
constante αC dans la déﬁnition de mC est choisie de telle façon qu’en l’absence d’absorption, la magnitude apparente est égale à la magnitude absolue si R = 10 pc
ÉC
E
L
O
T
Y
L
PO
mC = MC + 5 log(d/10 pc) + AC
C = U, B, V, R, I
Le « coeﬃcient d’extinction » AC , prend en compte l’absorption interstellaire ou
intergalactique. La longuer d’absorption, qui correspond à AV ∼ 1 est typiquement
∼ 1 kpc dans le plan de la galaxie, mais il varie considérablement suivant la ligne
de visée à cause de la présence de nuages absorbants. Perpendiculairement au plan
galactique, l’absorption d’une source extragalactique est typiquement de 10% (AV ∼
0.1).
On remarquera qu’en l’absence d’une absorption dépendant de la longueur d’onde,
l’indice de couleur d’un objet est le même que son indice de couleur apparent, par
exemple mB − mV = B − V = MB − MV . En réalité, l’absorption est plus intense aux
courtes longueurs d’onde, et en présence d’absorption un objet est « rougi ». La table
D.1 donne l’absorption relative typique du milieu interstellaire dans la Voie Lactée.
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
E
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
ÉC
N
H
EC
T
Y
L
PO
E
L
O
E
U
IQ
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
E
T
Y
L
PO
N
H
EC
E
U
IQ
E
L
CO E
ÉAnnexe
Solutions des exercices
Chapitre 1
1.1
T
Y
L
PO
N
H
EC
E
U
IQ
Si ΩM = ΩT = 1, alors ΩM (a) = ΩT (a) = 1 pour tout a(t). La formation de
structures se poursuit indéﬁniment au fur et à mesure que des régions d’énergie newtonienne négative de plus en plus grandes se détachent de l’expansion.
La valeur des Ω pour les modèles ΩM = ΩT = 0.3 et ΩM = 0.3, ΩΛ = 0.7 est
montrée sur la ﬁgure E.1.
1.2
ÉC
E
L
O
L’univers est en, expansion aujourd’hui parce qu’il l’était hier (voir (1.53)). Il était
en expansion hier parce que.....
Il sera diﬃcile d’obtenir une explication ultime car la réponse à cette question
demande de connaître les lois de la physique au Début des Choses.
Chapitre 2
2.1
Le ﬂux provenant d’une galaxie typique de redshift z 1 est
φ ∼
H
C
TE
2 × 1010 L /(2eV/photon)
∼ 100 m−2s−1 /z2 .
4π(zdH )2
Y
L
PO
U
Q
I
N
(5.1)
Le rapport du ﬂux des galaxies proches et de celui des étoiles proches est
ÉC
E
L
O
2 × 1010 L /(1 Mpc)2
∼ 2 × 10−2 .
L /(1 pc)2
347
(5.2)
E
348
ÉC
E
U
IQ
Annexe E. Solutions des exercices
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
T
Y
L
PO
N
H
EC
E
U
IQ
Fig. E.1: Les courbes continues montrent ΩM (a) et ΩΛ (a) pour (ΩM = 0.3, ΩΛ = 0.7). La
courbe pointillée montre ΩM (a) pour (ΩM = ΩT = 0.3). L’univers demeure dominé par la
matière pendant une durée plus longue dans le premier cas.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
2.2
T
Y
L
PO
N
H
EC
E
U
IQ
349
Le nombre total de photons stellaires peut être estimé grossièrement comme suit :
nstellaires ∼ J0 H0−1 /(2 eV/photon) ∼ 108 L Mpc−3 H−1
0 /2
ÉC
E
L
O
∼ 2 × 103 m−3 ,
(5.3)
qui est bien inférieur au nombre de photons du CBR.
Le nombre de noyaux d’hydrogène qui ont été transformés pour produire ces photons est
np→4 He ∼ 2000 m−3
2 eV
∼ 0.6 × 10−3 m−3 ,
6 MeV
(5.4)
E
U
IQ
ou encore 0.3 × 10−2 de l’hydrogène disponible.
Une petite quantité seulement de l’hydrogène a été transformé puisque la plus
grosse partie est encore dans l’espace intergalactique.
2.3
T
Y
L
PO
N
H
EC
La diﬀusion Compton domine avec un libre parcours moyen de l’ordre de
ÉC
E
L
O
(ne (t0 )σT )−1 ∼ 600dH ,
(5.5)
où nous avons supposé que toute la matière est ionisée (comme le suggère l’eﬀet
Gunn-Peterson).
2.4
La série de Balmer correspond à des énergies de photons de
En>2 = (1/2)α2 me c2 2−2 − n−2 ,
(5.6)
et des longueurs d’onde
λn>2 = 364.6 nm
1/4
,
1/4 − 1/n2
c’est-à-dire
λ3 = 656.3 nm
H
C
TE
λ4 = 486.1 nm ........
Y
L
PO
(5.7)
U
Q
I
N
(5.8)
La « cassure de Balmer » près du seuil d’ionisation λ∞ = 364.5 nm est due à la
photoionization et à l’absorption par des raies de Balmer de petit espacement.
Les étoiles dont les photosphères contiennent un nombre appréciable d’atomes
d’hydrogène dans l’état n = 2 montrent une forte absorption à des longueurs d’ondes
du côté bleu de la cassure de Balmer.
ÉC
E
L
O
E
350
E
U
IQ
Annexe E. Solutions des exercices
T
Y
L
PO
N
H
EC
Les spectres stellaires ont également, en général, une « cassure de Lyman » vers
λ = 91.1 nm qui correspond à l’ionisation depuis l’état fondamental de l’hydrogène
atomique. Cela se produit dans l’ultraviolet lointain et n’est donc pas observable par
des télescopes terrestres sauf pour les galaxies de redshift z > 4.
En utilisant la raie de Balmer Hβ (n = 2 → n = 4) on trouve que les deux galaxies
de la Fig. 2.9 ont des redshifts de ∼ 543/486.1 − 1 ∼ 0.117 et ∼ 523/486.1 − 1 ∼ 0.076.
ÉC
E
L
O
2.5
Il est possible de compter le nombre de galaxies avec un redshift inférieur à z. Le
volume de l’espace correspondant est V = (4π/3)z 3 d3H ∝ h−3
70 et le nombre volumique
mesuré est ∝ h370 .
Les luminosités sont déterminées en multipliant un ﬂux mesuré par (zdH )2 et sont
donc proportionnelles à h−2
70 . La densité de luminosité J0 ∼ ngal Lgal donnée par (2.9)
est donc proportionnelle à h70 .
Les masses galactiques sont déterminées à partir de la courbe de rotation, M ∼
v 2 r/G. La distrance radiale r est proportionnelle à la taille angulaire mesurée et par
la distance déterminée par redshift. La masse est donc proportionnelle à h−1
70 .
En multipliant par ngal on obtient une densité de masse associée aux galaxies
(2.10) proportionnelle à h270 . En divisant par la densité critique, on obtient un Ω
(2.11) indépendant de h70 .
2.6
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
Pour les céphéides de NGC1365 (Fig. 2.26) on a
V (10 jours) ∼ 27.5 ,
(5.9)
alors que pour les céphéides du LMC (Fig. 2.5) on a
V (10 jours) ∼ 14.3 ,
(5.10)
si bien que le rapport des distances est
R(NGC1365)
∼ 10(27.5−14.3)/5 ∼ 436. .
R(LMC)
H
C
TE
U
Q
I
N
(5.11)
E
Pour une distance du LMC de 50 kpc, cela donne une distance de 21.8 Mpc à NGC1365.
Pour une vitesse de récession de 1441 km sec−1 on obtient donc H0 = 65 km sec−1 Mpc−1 .
2.7
E
L
O
Y
L
PO
La distance de A496 est d’après la loi de Hubble
ÉC
R ∼ H0−1 × 9885 km sec−1 ∼ 141h−1
70 Mpc .
(5.12)
T
Y
L
PO
N
H
EC
E
U
IQ
351
Le rayon de A496 est environ 3000 arcsec ou encore
rc ∼ 2.0 h−1
70 Mpc .
E
L
O
(5.13)
Les amas de galaxies ont des dispersions en vitesse à peu près indépendantes de
la distance au centre de l’amas ce qui implique un proﬁl de densité de la forme
ÉC
ρ(r) ∼
M
,
4πrc r2
(5.14)
où M et rc sont la masse totale et le rayon de l’amas. (Bien entendu, cette forme ne
peut pas être valable près de r = 0.)
L’énergie gravcitationnelle de l’amas est
rc
GM (r)
−GM 2
Egrav = −
ρ(r)4πr2 dr ∼
.
(5.15)
r
rc
0
E
U
IQ
En vertu du théorème du viriel, cela doit être, en valeur absolue, le double de l’énergie
cinétique de l’amas. Le carré de la dispersion en vitesse suivant la ligne de visée, σv ,
est le double de la moyenne du carré de la vitesse (c’est évident pour des orbites
circulaires puisque sin2 ωt = 1/2). On a donc
LY T
(1/2)M (2σv2 ) = (1/2)
O
P
E
L
ÉCO
ce qui donne
M ∼
N
H
EC
GM 2
,
rc
2σv2 rc
14
∼ 4.8 h−1
70 × 10 M ,
G
(5.16)
(5.17)
pour σv = 715km sec−1 .
Cette détermination de la masse totale suppose évidemment que la dispersion en
vitesse des galaxies est la même que celle de la matière noire.
12
Pour une luminosité de 2 h−2
70 10 L , le rapport masse-luminosité est, en utilisant
la masse calculée par le viriel, M/L ∼ 230M/L . En supposant que cela est représentatif de l’univers dans son ensemble, on peut estimer la densité de masse à partir
de la densité de luminosité
ρM ∼ J0 (M/L) ∼ (1.2 h70 × 108 L Mpc−3 ) × 230
∼ 2.8 h270 × 1010 M Mpc−3 ,
ce qui donne
ΩM ∼ 0.2 .
Y
L
PO
U
Q
I
N
(5.18)
H
C
TE
(5.19)
Si l’on suppose que le rapport de la masse baryonique à la masse totale de A496
est représentatif de l’univers dans son ensemble, on trouve
E
L
O
ΩM ∼ 0.04 h−2
70
ÉC
14
2.4h−1
50 × 10 M
−5/2
3.45h50
× 1013 M
−1/2
∼ 0.47h70
,
(5.20)
E
352
E
U
IQ
Annexe E. Solutions des exercices
2.8
T
Y
L
PO
N
H
EC
La vitesse moyenne de récession de NGC 5033 est ∼ 875km sec−1 ce qui correspond
à une distance de
ÉC
E
L
O
R = 4300 h−1
70 Mpc
875
= 12.5 h−1
70 Mpc
300 × 103
(5.21)
À cette distance, le rayon visuel de 3 arcmin correspond à un rayon de
r =
3 π
−1
12.5 h−1
70 Mpc ∼ 11 h70 kpc .
60 180
(5.22)
L vitesse de rotation loin du centre galactique est
v =
1
1070 − 690
∼ 210 km sec−1 ,
2
sin(65 deg)
N
H
EC
E
U
IQ
(5.23)
où nous avons utilisé l’angle d’inclinaison donné dans la publication.
Cela donne une masse à l’intérieur de 6 arcmin par rapport au centre de
T
Y
L
PO
M =
E
L
O
v2 r
∼ 2.2 × 1011 h−1
70 M .
G
La magnitude absolue est
ñ
ÉC
MV
6
12.5h−1
70 × 10 pc
= 10.1 − 5 log
10 pc
(5.24)
ô
= −20.4 + 5 log h70 ,
(5.25)
ce qui correspond à une luminosité de
L
10
= 100.4(4.64+20.4−5 log h70 ) = 1.0 h−2
.
70 × 10
L
(5.26)
Le rapport masse-luminosité à l’intérieur de 6 arcsec est alors
M
M
= 22h70
.
L
L
2.9
La vitesse de rotation des deux composantes est
Y
L
PO
(5.27)
H
C
TE
475 − 135
v ∼
∼ 170 km sec−1 ,
2
E
L
O
U
Q
I
N
(5.28)
ce qui, pour une période de 5.72 jours correspond à une distance entre objets de
∼ 2.7 × 1010 m ou ∼ 38R . Cela donne une masse réduite de ∼ 5.8M soit environ
10M par objet.
ÉC
E
T
Y
L
PO
N
H
EC
E
U
IQ
353
Les éclipses durent environ 15% d’une période ce qui donne un diamètre stellaire
de ∼ 1.3 × 1010 m soit un rayon stellaire de ∼ 9R .
En utilisant D/R ∼ 9.5 × 10−12 , on trouve une distance du système d’environ
43 kpc.
En prenant comme distance du LMC 45.7kpc, la relation de luminosité apparente
V = −2.765 log P +17.044 donne une luminosité absolue de MV = 2.765 log P −1.256.
Cette valeur est de 0.2 magnitudes moins brillante que dans le calibrage de Hipparcos.
En utilisant le calibrage de Hipparcos (céphéides les plus brillantes) on obtiendrait
des distances de galaxies environ 10% plus grandes, ou une valeur de H0 plus petite
de 10%.
ÉC
E
L
O
2.10
E
U
IQ
Considérons une sphère d’hydrogène ionisé contenant Np protons et Np électrons.
L’équation de l’équilibre hydrostatique pour une sphère en autogravitation est
GM (r)ρ(r)
dP
= −
, ,
dr
r2
C
E
T
LY
HN
(5.29)
où P (r) est la pression, M (r) la masse contenus à l’intérieur d’un rayon r, et ρ(r)
la densité de masse. Le produit de la pression moyenne P par le volume total V =
(4π/3)R3 est
R
R
dP
ρ(r)dr ,
(5.30)
PV =
P (r)4πr2 dr = −
(4π/3)r3
dr
0
0
O
P
E
L
ÉCO
où, dans la deuxième forme, nous avons intégré par parties et utilisé le fait que P (R) =
0. En utilisant pour le gradient de pression la valeur à l’équilibre hydrostatique, on
trouve
R
−Eg
GM (r)
ρ(r)4πr2 dr =
,
(5.31)
P V = 1/3
r
3
0
où Eg est l’énergie potentielle gravitationnelle totale de la sphère. En utilisant la loi
des gaz parfaits, on obtient une expression pour la température moyenne T :
2Np kT = −Eg /3 .
(5.32)
U
Q
I
N
Puisque l’énergie cinétique moyenne par particules est (3/2)kT , on obtient une forme
du théorème du viriel qui dit que l’énergie cinétique par particule es la moitié de (la
valeur absolue de) l’énergie potentielle par particule :
Y
L
PO
2Np (3/2)kT = (1/2)|Eg | .
H
C
TE
(5.33)
Pour une densité uniforme, on peut évaluer (5.31) pour trouver
ÉC
E
L
O
kT = (β/10)
Gm2p Np
R
β=1.
(5.34)
E
354
E
U
IQ
Annexe E. Solutions des exercices
T
Y
L
PO
N
H
EC
Dans une étoile réelle, il y a un proﬁl de densité. La masse est davantage concentrée
près du centre, si bien que le rayon eﬀectif est inférieur à R. Par conséquent, une étoile
serait caractérisée par un β > 1. La distribution plus réaliste ρ ∝ r−2 donne β = 5/3.
Le nombre volumique de photons à l’équilibre thermique est 2.4T 3/π 2 si bien que
le nombre de photons dans l’étoiles est approximativement
Å
ã
mp 6
,
(5.35)
Nγ = (4π/3) (2.4/π 2 )(β 3 /1000)Np3
mpl
ÉC
E
L
O
ou
Å
ã
Nγ
mp 6
= (4π/3) (2.4/π 2 )(β 3 /1000)Np2
Np
mpl
= 0.30 × 10−3 β 3
Å
M
M
ã2
,
N
H
EC
E
U
IQ
(5.36)
où M = Np mp est la masse de l’étoiles. Pour le Soleil, β ∼ 2 et Nγ ∼ 0.003Np. Puisque
le nombre de photons est proportionnel au cube du nombre de protons, les étoiles de
masse M ∼ 30M ont un nombre comparable de photons et de protons. Par coséquent,
pour de telles étoiles, la pression de radiation ργ /3 ∼ nγ kT est comparable à la
pression des protons et des électrons 2np kT . Pour des masses supérieures, les étoiles
sont instables car l’énergie thermique Eth = 3Np kT +ργ V et l’énergie gravitationnelle
Eg = −3P V = −6Np kT − ργ V deux bien supérieures à l’énergie totale Eth + Eg =
−3NpkT . Dans de telles condition, de petites ﬂuctuations de la densité de photons
peuvent détruire l’équilibre hydrostatique et l’étoile rejette de la masse jusqu’à ce que
la température atteigne une valeur acceptable.
L’énergie thermique totale des photons est
ÉC
E
L
O
T
Y
L
PO
ργ V ∼ (4π/3)R3 × 2
π2
(kT )4 (c)−3
30
(5.37)
Les photons ont une marche aléatoire dans le Soleil jusqu’à ce qu’ils s’échappent
à la surface. Pour une série de N pas de taille λi , la valeur moyenne du carré de le
distance de la poisition d’un photon par rapport à l’origine est
N
N
N
2
λi ·
λj
|λi |
(5.38)
=
= N |λ|2 ,
i=1
j=1
i=1
H
C
TE
U
Q
I
N
où nous avons supposé que les diﬀusions rendent la direction de propagation complètement aléatoire λi · λj = 0 pour i = j. En égalant ce nombre avec la carré du
rayon solaire, on peut obtenir une évaluation du temps moyen mis par un photon
pour atteindre la surface
ÉC
E
L
O
Y
L
PO
τ = N λ/c ∼ (R/c)
R
,
λ
(5.39)
E
T
Y
L
PO
N
H
EC
E
U
IQ
355
où λ = 1/(nσ) est le libre parcours moyen des photons. En prenant n = Np /V , le
libre parcours moyen est
ÉC
E
L
O
(4π/3)R3
∼ 0.018 m
λ ∼
Np σ
Å
R
R
ã3
M σT
,
M σ
(5.40)
ce qui donne un temps d’échappement de
τ ∼ (9/4π)
Np σ
,
Rc
(5.41)
où σ est la section eﬃcace de diﬀusion des photons. Si les électrons sont complètement
ionisés, σ = σT mais nolus l’écrivons comme σ = κσT avec κ > 1 pour garder trace
des atomes non-ionisés dans les couches externes du Soleil. On a donc
τ ∼ (9/4π)
M R
Np κσT
∼ 0.8 × 104 an κ
.
Rc
M R
N
H
EC
E
U
IQ
(5.42)
En divisant l’énergie totale des photons par le temps moyen d’échappement, on
obtient une setimation de la luminosité
Å
ã
32π 4
mp 8 c2
−4 4 −1 3
∼ 10 β κ Np
L =
27 × 30
mpl
σ
ÉC
E
L
O
T
Y
L
PO
Å
∼ 1.1 × 10
26
M
W
M
ã3
β 4 κ−1 ,
(5.43)
ce qui est en bon accord avec L = 3.8 × 1026 W.
2.11
Le libre parcours moyen d’un photon dans un gros amas de masse ∼ 1014 h−1 M
et de diamètre D ∼ 1h−1 Mpc est
λ−1 ∼ ne σT ∼
1014 h−1 M
(1h−1 Mpc)−3 σT
mp
H
C
E
λ
mp
(1h−1 Mpc)2
∼
∼ 10−71 × 1073 ∼ 100 .
14
−1
D
10 h M
σT
T
Y
POL
(5.44)
U
Q
I
N
(5.45)
Par conséquent, les amas sont assez transparents à leurs propres photons. Cela n’est
pas pour surprendre puisque l’on peut voir clairement les galaxies individuelles dans
les amas.
La section eﬃcace de Rutherford électron-proton à grand angle est de l’ordre de
σT /(v/c)4 ∼ σT (me /T )2 . Pour T ∼ 5 keV, cela donne une section eﬃcace de 104 σT et
ÉC
E
L
O
E
356
E
U
IQ
Annexe E. Solutions des exercices
T
Y
L
PO
N
H
EC
un libre parcours moyen eﬀectif des électrons de D/100. Le gaz électron-proton peut
donc être considéré comme un ﬂuide en équilibre thermique.
Le produit de la section eﬃcace de bremsstrahlung par la vitesse, moyenné sur la
distribution thermique, est
∑
≠
ασT c c ασT c me 1/2
dσ
=
∼
.
(5.46)
v
dEγ T
Eγ
v T
Eγ
T
ÉC
E
L
O
La luminosité est
L ∼ D3 n2p
≠
T
dEγ
v
0
dσ
dEγ
∑
Eγ ∼ n2p αcσT
me T D 3 .
(5.47)
T
Puisque D = θR où θ est la taille angulaire d’un amas à la distance R. De plus,
Np ∼ np D3 , par conséquent
√
Np2 αcσT me T
L ∼
.
R3 θ 3
Le ﬂux est donné par
(5.48)
√
Np2 αcσT me T
∼
,
R5 θ 3
O
P
E
L
ÉCO
φx
C
E
T
LY
HN
E
U
IQ
(5.49)
qui est le résultat recherché.
Pour trouver la masse totale de l’amas à partir de la température en rayons X, on
modiﬁe (5.29) de façon que le gradient de pression ne supporte que les baryons
dP
GM (r)ρ(r)f
= −
, ,
dr
r2
(5.50)
où f est la fraction de la masse totale de l’amas qui se trouve sous forme de baryons.
En suivant le même raisonnement que dans l’exercice 2.10, on trouve
6kT
|Egrav |
=
∼
mp
Mtot
GMtot
,
Rθ
(5.51)
U
Q
I
N
où Rθ est le rayon de l’amas, ce qui détermine la masse totale de l’amas.
Chapitre 3
3.1
Y
L
PO
Le résultat provient de la chaîne
ÉC
E
L
O
dτ 2 = ηµν dx̃µ x̃ν = ηµν
H
C
TE
∂ x̃µ α ∂ x̃ν β
dx
dx
∂xα
∂xβ
(5.52)
E
N
H
EC
E
U
IQ
= ηαβ dxα dxβ .
T
Y
L
PO
L’équation (3.108) équivaut à
ÉC
E
L
O
Å
1 =
Å
−1 =
∂ x̃0
∂xj
∂ x̃0
∂x0
ã2
−
ã2
−
(5.54)
∂x0
ã2
3 Å
∂ x̃i
i=1
(5.53)
ã2
3 Å
∂ x̃i
i=1
∂xj
357
j = 1, 3 .
(5.55)
Ces équation sont évidemment satisfaites pour des boosts ou des rotations, par exemple
−1 = −(cos2 θ + sin2 θ) ,
et
1 = γ2 − β2γ2 .
3.2
T
Y
L
PO
(5.56)
N
H
EC
L’équation de la géodésique est
Å
ã
d
∂gµλ dxµ dxλ
dxµ
= 0
gµν
− (1/2)
dτ
dτ
∂xν dτ dτ
ÉC
E
L
O
E
U
IQ
(5.57)
ν = 0, 3 .
(5.58)
Pour gµν = ηµν toutes les dérivées de la métrique s’annulent et l’équation de la
géodésique est
Å
ã
d dxµ
= 0,
(5.59)
ηµν
dτ dτ
ce qui implique que la quadri-vitesse dxµ /dτ est constante.
3.3
La fusée est en chute libre après la libération des dernières tuyères, elle suit donc
une géodésique. L’horloge de la fusée doit, par conséquent, mesurer un temps écoulé
plus long que l’horloge restée au sol, qui, elle, n’est pas en chute libre. D’un autre côté
un avion n’est pas en chute libre et la réponse dépend de sa vitesse et de son altitude.
Pour un potentiel gravitationnel Φ = gz, le temps propre est donné par
Y
L
PO
H
C
TE
U
Q
I
N
dτ 2 = dt2 (1 + 2gz) − (1 − 2gz)dr2 .
E
L
O
(5.60)
Pour une fusée lente se déplaçant verticalement suivant (z), cela devient
1/2
dτ = dt 1 + 2gz − ż 2
= dt 1 + 2gz − (1/2)ż 2 ,
ÉC
(5.61)
E
358
E
U
IQ
Annexe E. Solutions des exercices
T
Y
L
PO
N
H
EC
où nous négligeons les termes d’ordre supérieur en gz et ż.
L’équation newtonienne pour une vitesse de décollage de v0 est
ÉC
E
L
O
ce qui donne
z(t) = v0 t − (1/2)gt2 ,
(5.62)
dτ = dt 1 + 2gz − v02 /2 ∼ dt(1 + 2gz)(1 − v02 /2) .
(5.63)
En intégrant cette expression sur le vol de la fusée de t = 0 à t = 2v0 /g on trouve
τ (t = 2v0 /g) − τ (t = 0) =
2v0 1 + 6v02 /c2 ,
g
(5.64)
E
U
IQ
par conséquent, l’horloge de la fusée compte un temps supérieur à l’horloge restée
sur Terre, comme on s’y attend. On montre facilement que la comparaison des deux
horloges ne dépend pas de notre choix Φ(z = 0) = 0.
Pour un avion volant à une altitude h on a
dτ = dt 1 + gh − v 2 /2 ,
(5.65)
T
Y
L
PO
N
H
EC
et la comparaison entre l’horloge de l’avion et celle restée sur Terre dépend des valeurs
de h et v.
3.4
ÉC
E
L
O
Pour une particule lente on a dx0 /dτ ∼ 1 et dxi /dτ ∼ 0, si bien que l’équation de
la géodésique est
Å
ã
d
dxµ
∂g00
ν = 0, 1, 2, 3 .
(5.66)
gµν
= (1/2) ν
dτ
dτ
∂x
Avec g00 = 1 + 2Φ et gii = −1 + 2Φ, l’équation ν = i est (en négligeant les termes
proportionnels à la vitesse)
∂Φ
d2 xi
= − i
dτ 2
∂x
i = 1, 2, 3 ,
H
C
TE
U
Q
I
N
(5.67)
qui est le résultat newtonien.
L’équation ν = 0 donne les taux relatifs des horloges stationnaires et en mouvement :
ï
ò
d
dx0
dx0
(1 + 2Φ)
=0
⇒ (1 + 2Φ)
= constant ,
(5.68)
dτ
dτ
dτ
ÉC
E
L
O
Y
L
PO
ce qui est la forme générale de (5.63).
E
3.5
T
Y
L
PO
N
H
EC
E
U
IQ
359
Puisque les courbes de θ constant sont perpendiculaires aus courbes de φ constant,
la relation
ÉC
E
L
O
dS 2 = a2 (dχ2 + sin2 χdθ2 )
(5.69)
découle du théorème de Pythagore.
√
Pour r = sin χ, on a dr = 1 − r2 dχ d’où il découle que
ï
ò
dr2
2
2
+
r
dθ
.
dS 2 = a2
1 − r2
(5.70)
Considérons un objet de taille dS qui s’étend de (χ1 , θ) à (χ1 , θ + dθ) avec dS =
ar1 dθ. Les photons émis vers le pôle χ = 0 des extrémités de l’objet vont suivre des
chemins de θ constant si bien que l’objet semblera avoir une taille angulaire
dS
.
dθ =
ar1
C
E
T
LY
HN
E
U
IQ
(5.71)
Si la sphère est en expansion, les photons vont toujours suivre des courbes de θ
constant car la symétrie sphérique (vue du centre de la sphère) est maintenue. les
photons n’ont pas de direction privilégiée vers laquelle ils puissent être déviés. Dans
ce cas, la taille angulaire est
O
P
E
L
ÉCO
dθ =
dS
,
a(t1 )r1
(5.72)
où t1 est l’instant d’émission. On obtient donc la même relation distance-taille angulaire que (3.68).
À t0 , les photons sont distribués uniformément sur un cercle de rayon a0 χ1 et de
circonférence 2πa0 r1 . Le ﬂux d’énergie est donc
F =
L
,
2πa0 r1 (1 + z)2
(5.73)
où les facteurs 1 + z prennent en compte le redshift et la « dilatation du temps » due
à l’expansion de la sphère. Cette relation peut être comparée à (3.64).
3.6
H
C
TE
Avec la contrainte x2 + y 2 + z 2 + w2 = a2 , la métrique spatiale est
Y
L
PO
dS 2 = dx2 + dy 2 + dz 2 +
E
L
O
(xdx + ydy + zdz)2
.
a2 − x2 − y 2 − z 2
U
Q
I
N
(5.74)
En utilisant les transformations x = ra sin θ cos φ, y = ra sin θ sin φ, et z = ra cos θ,
on trouve la métrique de Robertson-Walker avec k = 1.
ÉC
E
360
E
U
IQ
Annexe E. Solutions des exercices
3.7
T
Y
L
PO
N
H
EC
Toutes les géodésiques passant par un point passent par son antipode et vice versa.
E
L
O
3.8
ÉC
À l’ordre z 2 , on trouve d1 = dA < d0 < dL . Les distances diﬀèrent dans le
coeﬃcient du terme en z 2 elles diﬀèrent donc de ∼ 10% à z ∼ 0.1 ou R ∼ 430h−1
70 Mpc.
3.9
Si un observateur comobile voit l’explorateur partir avec une vitesse v, alors
dχ
dR
= a
= v.
dt
dt
(5.75)
E
U
IQ
La dérivée porte sur la variable t puisque c’est le temps mesuré par l’horloge comobile.
En utilisant la métrique, on trouve
N
H
EC
dχ
v
√
=
dτ
a0 1 − v 2
ÉC
E
L
O
T
Y
L
PO
dt
1
= √
.
dτ
1 − v2
(5.76)
(5.77)
Dans un univers vide (a ∝ t), la galaxie la plus lointaine qui puisse être atteinte a un
redshift de z = v/c (pas vraiment surprenant). Pour un univers critique (a ∝ t2/3 ),
la galaxie la plus lointaine qui puisse être atteinte a un redshift de z = 2v/c. Un
simple argument newtonien peut expliquer la distance supplémentaire dans un univers
critique.
3.12
Les photons suivent des courbes de pente unité. On a donc
vt2 = t2 − t1
vt3 = t4 − t3 ,
ce qui implique
t2 =
t1
1−β
t3 =
H
C
TE
t4
.
1+β
Y
L
PO
(5.78)
U
Q
I
N
(5.79)
Le postulat de dilatation des temps implique que l’horloge en mouvement mesure un
temps plus court d’un facteur γ :
ÉC
E
L
O
t2 =
t1
γ(1 − β)
t3 =
t4
.
γ(1 + β)
(5.80)
E
N
H
EC
E
U
IQ
361
Le temps t est alors donné par
ï
ò
ï
ò
t + t2
1
t4
t1
t4 + t 1
β(t4 − t1 )
= γ
t = 3
=
+
−
2
2γ 1 + β
1−β
2
2
ÉC
E
L
O
T
Y
L
PO
= γt − βγx ,
(5.81)
comme on s’y attend pour une transformation de Lorentz. De même, on a
ï
ò
ï
ò
1
t4
t1
t4 − t1
β(t4 + t1 )
t − t2
x = 3
=
−
= γ
−
2
2γ 1 + β
1−β
2
2
= γx − βγt .
E
U
IQ
(5.82)
Aﬁn de démontrer la formule de contraction de Lorentz, nous supposons que B
mesure la longueur du barreau par radar, en émettant deux photons à t = −L/2
et en recevant les échos à t = L/2. B voit une contraction de Lorentz car, par le
postulat (3.5), l’hologe de B mesure t = ±0.5L 1 − β 2 et conclut par conséquent
que le barreau a une longueur L = L 1 − β 2 .
Chapitre 4
4.1
ÉC
E
L
O
T
Y
L
PO
N
H
EC
Pour ä = 0 et pour dr = 0 (pour une horloge comobile), on a
dT = dt + (1/2)(ȧ/a)2 (ar)2 dt = dt + (1/2)v 2 dt ,
(5.83)
où v = HR est la vitesse de Hubble de l’horloge comobile. Cela donne
dt =
dT
∼ dT (1 − v 2 /2)
1 + v 2 /2
(5.84)
C’est le résultat prévu par la relativité restreinte où l’on s’attend à ce que le temps
dt mesuré par l’horloge en mouvement
soit plus court que le temps dT mesuré par
√
l’horloge stationnaire d’un facteur 1 − v 2 ∼ 1 − v 2 /2.
Au second ordre, la trajectoire du photon de la Fig. 4.1 entre ta et t est régie par
t
H(t)
(t − ta )2 .
a(t)χ ∼
dt (1 − H(t)(t − t)) = (t − ta ) +
(5.85)
2
ta
Pour la trajectoire entre t et tb on a
ÉC
E
L
O
Y
L
PO
a(t)χ ∼ (tb − t) −
H
C
TE
H(t)
(tb − t)2
2
U
Q
I
N
(5.86)
E
362
E
U
IQ
Annexe E. Solutions des exercices
T
Y
L
PO
En ajoutant les deux on trouve
E
L
O
a(t)χ ∼
N
H
EC
H(t) (tb − t1 )
+
(t − ta )2 − (tb − t)2 .
2
4
(5.87)
Puisque, au premier ordre, (t − ta ) et (tb − t) sont tous deux égaux a(t)χ, le deuxième
terme s’annule à l’ordre χ2 et l’on a
ÉC
a(t)r ∼
(tb − t1 )
+ O(r3 )
2
(5.88)
où nous avons fait usage de ce que χ = r + O(r3 ). En prenant la diﬀérence entre les
deux trajectoires, on a
0 = tb + ta − 2t −
H(t) (tb − t)2 + (t − ta )2 .
2
En utilisant (t − ta ) ∼ (tb − t) ∼ a(t)r, on trouve
N
H
EC
tb + t a
= t + (1/2)aȧr2 + O(r3 )
2
qui est équivalent à (4.11).
4.2
ÉC
E
L
O
T
Y
L
PO
(5.89)
E
U
IQ
(5.90)
Le tenseur de Ricci à l’origine d’un système de coordonnées en chute libre est
donné par
Rβγ = η γδ Rαβγδ
ñ
= 1/2 η
∂ 2 gβα
∂ 2 gγγ
∂ 2 gδγ
∂ 2 gβδ
+
−
−
∂xα ∂xγ
∂xβ ∂xδ
∂xα ∂xδ
∂xβ ∂xγ
γδ
ô
.
(5.91)
Le scalaire de Ricci est
R = η γδ Rγδ = η αγ
Les dérivées sont
∂Rδµ
∂xµ
ñ
= (1/2)
∂ 3 gγγ
η µβ µ β δ
∂x ∂x ∂x
et
E
L
O
ηδµ
ÉC
∂ 2 gδδ
∂ 2 g γδ
−
∂xα ∂xγ
∂xγ ∂xδ
ce qui prouve le résultat recherché.
−
∂Rδµ
∂R
=
2
,
∂xµ
∂xµ
H
C
E
∂ 3 g αµ
∂xµ ∂xα ∂xδ
T
Y
POL
ô
,
U
Q
I
N
(5.92)
(5.93)
E
T
Y
L
PO
4.3
N
H
EC
E
U
IQ
363
Pour un gaz parfait non-relativiste, E ∼ m et p2 /2m = (3/2)T d’où il découle
que p = nT mT = ρ. Pour un gaz parfait relativiste, p = E d’où il découle que
p = ρ/3.
La quadri-divergence de T µν pour un ensemble de particules est
ò
ï
∂T µν
3
µ ∂F
+ v · ∇R F .
=
d pp
(5.94)
∂xµ
∂t
ÉC
E
L
O
La quantité entre crochets s’annule en vertu du théorème de Liouville, ce qui prouve
que la quadri-divergence s’annule.
4.4
E
U
IQ
Considérons un système de coordonnées en chute libre x̃ et un autre système de
coordonnées x déﬁni par
xµ =
∂xµ α
x̃
∂ x̃α
N
H
EC
x̃α =
T
Y
L
PO
∂ x̃α µ
x ,
∂xµ
(5.95)
où les coeﬃcients de transformation ∂ x̃α /∂xµ sont des constantes qui satisfont
E
L
O
ηαβ
ÉC
∂ x̃α ∂ x̃β
= ηµν
∂xµ ∂xν
⇒
η αβ
∂ x̃α ∂ x̃β
= η µν .
∂xµ ∂xν
(5.96)
Le temps propre est donné par
dτ 2 = g̃µν dx̃µ dx̃ν = g̃µν
∂ x̃µ ∂ x̃ν α β
dx dx ,
∂xα ∂xβ
(5.97)
ce qui montre que la métrique est un tenseur
gαβ = g̃µν
∂ x̃µ ∂ x̃ν
.
∂xα ∂xβ
(5.98)
Puisque le système x̃ est en chute libre, on a
gαβ = [ηκλ + (1/2)g̃κλ,µν x̃µ x̃ν + .....]
∂ x̃κ ∂ x̃λ
.
∂xα ∂xβ
H
C
TE
En utilisant (5.96), on voit que le système x est aussi en chute libre
E
L
O
ô
∂ x̃κ ∂ x̃λ ∂ x̃µ ∂ x̃ν
xγ xδ + .....
+ (1/2) g̃κλ,µν α β γ
∂x ∂x ∂x ∂xδ
ñ
= ηαβ
ÉC
∂ x̃κ ∂ x̃λ
+ .....
∂xα ∂xβ
Y
L
PO
gαβ = ηαβ + (1/2)g̃κλ,µν x̃µ x̃ν
U
Q
I
N
(5.99)
(5.100)
E
364
E
U
IQ
Annexe E. Solutions des exercices
T
Y
L
PO
N
H
EC
La quantité entre crochets est gαβγδ et, apparemment, c’est un tenseur. Puisque
Rαβγδ est la somme de termes de cette forme, il s’ensuit que c’est également un
tenseur.
On montre facilement que le « tenseur de Ricci » est également un tenseur :
ÉC
E
L
O
Rβδ = η αγ Rαβγδ = η αγ
= η κµ R̃κλµν
∂ x̃κ ∂ x̃µ
∂ x̃λ ∂ x̃ν
R̃
κλµν
∂xα ∂xγ
∂xβ ∂xδ
∂ x̃λ ∂ x̃ν
∂ x̃λ ∂ x̃ν
=
R̃
.
λν
∂xβ ∂xδ
∂xβ ∂xδ
(5.101)
De façon analogue, on trouve que ηµν η αβ Rαβ est un tenseur. Il s’ensuit que Gµν est un
tenseur. L’équation d’Einstein relie, par conséquent, deux tenseurs (G et T ) et si elle
est valable dans un référentiel en chute libre, elle doit l’être dans tous les référentiels
qui lui sont reliés par une transformation de Lorentz.
4.5
N
H
EC
E
U
IQ
L’équation d’Einstein à l’origine d’un système de coordonnées en chute libre est
T
Y
L
PO
Rµν − (1/2)ηµν R = −8πGTµν ,
E
L
O
où le scalaire de Ricci est
ÉC
R = η µν Rµν .
(5.102)
(5.103)
En contractant l’équation d’Einstein avec η µν on obtient
−R = −8πGη µν Tµν .
(5.104)
En substituant cela dans l’équation d’Einstein on trouve
Rµν = −8πGTµν + 4πGηµν η αβ Tαβ ,
(5.105)
qui est le résultat recherché.
4.6
U
Q
I
N
Considérons une particule qui n’a que des interactions gravitationnelles dans un
objet sphérique de densité ρ. L’accélération de la particule est
4πGρ i
d2 xi
= −
x .
dt2
3
Y
L
PO
H
C
TE
(5.106)
Deux particules initialement au repos et séparées de δxi ont une accélération relative
de
ÉC
E
L
O
4πGρ
d2 δxi
= −
δ.
dt2
3
(5.107)
E
N
H
EC
E
U
IQ
365
La sépartaion invariante δ 2 = −ηµν δxµ δxν = (δxi )2 obéit à l’équation
E
L
O
T
Y
L
PO
d2 δ 2
d2 δ
4πGρ
δ − −2R1010 δ 2 ,
=
2δ
= −2δ
2
2
dt
dt
3
(5.108)
où nous avons fait usage de dδ/dt ∼ 0 et de dt ∼ dτ pour des particules au repos. On
en conclut que
ÉC
Ri0i0 =
4πGρ
.
3
(5.109)
Cela entraîne
R00 = η µν Rµ0ν0 = −4πGρ .
(5.110)
E
U
IQ
Ce résultat est en accord avec la deuxième forme de l’équation d’Einstein :
N
H
EC
R00 = −8πG [T00 − (1/2)g00 g µν Tµν ] = −4πGρ ,
T
Y
L
PO
(5.111)
si la pression est négligeable.
Pour des particules hors de la sphère de masse M , l’accélération newtonienne est
ÉC
E
L
O
d2 xi
GM
= − 3 xi .
2
dt
r
(5.112)
Pour deux particules séparées de δ dans la direction radiale, l’accélération relative est
∝ ∆(r−2 ) = −2δ/r3 . Pour deux particules séparées dans une direction non-radiale,
l’accélération relative est ∝ δ(r−3 ). Cela entraîne
R00 = (−2 + 1 + 1)GM/r3 = 0 .
(5.113)
4.7
Dans un univers vide on a
R = rt
T =t
1 + r 2 − t0 ,
donc, pour une particule de r ﬁxe on a
dR = rdt
ce qui implique
ÉC
E
L
O
dT = dt
H
C
TE
1 + r2 ,
Y
L
PO
r
dR
= √
< 1.
dT
1 + r2
U
Q
I
N
(5.114)
(5.115)
(5.116)
E
366
E
U
IQ
Annexe E. Solutions des exercices
4.8
T
Y
L
PO
N
H
EC
En utilisant l’équation (4.106) pour le tenseur d’Einstein dans le système de coordonnées orthogonal de métrique (3.18) on trouve
ÉC
E
L
O
G00 = −
∂ 2 g11
∂ 2 g22
∂ 2 g33
−
−
= −2∇2 Φ ,
∂x2 ∂x2
∂x3 ∂x3
∂x1 ∂x1
(5.117)
par conséquent la composante 00 de l’équation d’Einstein est
∇2 Φ = 4πρ .
(5.118)
Les autres composantes de Gµν s’annulent comme on s’y attend pour une pression
nulle.
Chapitre 5
5.1
Pour ΩT = ΩM = 0, on trouve
a(t) ∝ t
T
Y
L
PO
N
H
EC
E
U
IQ
a0 χ1 (z) = H0−1 ln(1 + z) .
q0 = 0
(5.119)
Utilisant a0 = H0−1 pour un univers vide, on trouve
ÉC
E
L
O
r1 (z) =
1 + z + (1 + z)−1
.
2
(5.120)
Pour ΩT = ΩM = 1, la taille angulaire minimum se produit pour z = 1.25.
Pour ΩT = ΩM = 1, on trouve
t0 = (2/3)H0−1
(5.121)
√
a0 χ1 (z) = a0 r1 (z) = 2H0−1 (1 − 1/ 1 + z) .
(5.122)
a(t) ∝ t2/3
q0 = 1/2
Pour ΩT = ΩΛ = 1, on trouve
a(t) ∝ exp(H0 t)
q0 = −1
t0 = ∞
a0 χ1 (z) = a0 r1 (z) = zH0−1 .
Pour ΩT = ΩM = 0, on trouve
a(t) ∝ t
ÉC
E
L
O
T
Y
POL
q0 = 0
H
C
E
t0 = H0−1
a0 χ1 (z) = H0−1 ln(1 + z) .
U
Q
I
N
(5.123)
(5.124)
(5.125)
(5.126)
E
N
H
EC
En utilisant a0 = H0−1 pour un univers vide, on trouve
E
L
O
T
Y
L
PO
E
U
IQ
1 + z − (1 + z)−1
.
2
r1 (z) =
367
(5.127)
L’âge de l’univers ΩT = ΩΛ = 1 serait évidemment change en incorporant de
l’énergie du rayonnement. La luminosité et les distances angulaires s’obtiennent en
multipliant ou en divisant a0 r1 par 1 + z.
Pour ΩT = ΩM = 1, la distance angulaire minimum se produit pour z = 1.25.
ÉC
5.2
L’équation devrait être une bonne approximation tant qu’il n’y a pas d’autres
espèces relativistes, c’est-à-dire pour T me . Après que les neutrinos commencent à
devenir non-relativistes, l’équation est toujours une bonne approximation car le terme
ΩM domine dans tous les cas. Pour trec on peut faire l’approximation que l’univers
est dominé par la matière dans quel cas l’âge est juste les (2/3) du temps de Hubble
à cette époque :
LY T
−1/2 3/2
ârec
trec = (2/3)H−1
0 ΩM
O
P
E
L
ÉCO
∼
N
H
EC
E
U
IQ
5
2.6 h−1
70 × 10 an
√
.
ΩM
(5.128)
Pour teq , on ne peut négliger ni le rayonnement ni la matière (à teq ) il faut donc
calculer une intégrale non-triviale :
teq =
(1.68Ωγ )3/2
H−1
0
Ω2M
0
1
ã2
Å
xdx
0.3
4
√
.
∼ 5 × 10 an
ΩM h270
1+x
(5.129)
Négliger la matière aurait donné le bon ordre de grandeur et la bonne dépendance en
ΩM h270 .
5.3
Pour ΩT = ΩM = 1 + on trouve
1
t0 = H0−1
0
= H0−1
da
1/2
a [(1 + )a−3 − a−2 ]
∼
1
E
L
O
H
C
TE
1/2
[1 + (1 − a)]
daa1/2 [1 − (1 − a)/2] ∼ (2/3)H0−1 (1 − /5) .
ÉC
0
a1/2 da
Y
L
PO
0
H0−1
1
U
Q
I
N
(5.130)
(5.131)
(5.132)
E
368
5.4
T
Y
L
PO
t0 ∼ (2/3)H0−1 [1 + ΩΛ /3 + ......]
E
L
O
5.5
ÉC
E
U
IQ
Annexe E. Solutions des exercices
N
H
EC
La relation
a0 χ1 (z) ∼ a0 r1 (z) = H0−1 z [1 − (1 + q0 )z/2 + .....]
(5.133)
a0 dχ1 = H0−1 dz [1 − (1 + q0 )z + .....] ,
(5.134)
implique
qui implique
a30 r12 dχ1 ∼ H0−3 z 2 dz [1 − 2(1 + q0 )z] .
5.6
T
Y
L
PO
N
H
EC
E
U
IQ
(5.135)
La probabilité de diﬀusion Compton sur les photons du CBR dans un amas de
galaxies de diamètre D est
E
L
O
P ∼ σT Dne = σT dA (z)∆θne ,
ÉC
(5.136)
où ∆θ est la taille angulaire observée de l’amas. La luminosité en rayons X de l’amas
est
(5.137)
L ∼ ασT c me c2 kT D3 n2e ,
ce qui donne un ﬂux d’énergie observé de
φ ∼ ασT c me c2 kT (dA ∆θ)3 n2e d−2
L ,
(5.138)
où nous n’avons pas tenu compte des facteurs numériques. En divisant P 2 par φ et
en réarrageant les termes, on trouve
√
P 2 αc me c2 kT ∆θ n2e .
(5.139)
a0 χ1 (z) ∼
(1 + z)3 φσT
ne 2
5.7
Y
L
PO
H
C
TE
U
Q
I
N
La luminosité d’un corps noir de rayon D est L = πD 2 σT 4 . Le ﬂux d’énergie
mesuré est
ÉC
E
L
O
φ =
L
D2 σT 4
=
.
2
4πdL
4(a0 χ1 (1 + z))2
(5.140)
E
T
Y
L
PO
N
H
EC
E
U
IQ
369
Le diamètre de la photosphère d’une supernova peut être estimé à partir de la vitesse
d’expansion de la photosphère, v :
ÉC
E
L
O
D =
2vt
,
1+z
(5.141)
où t est le temps d’observation depuis l’explosion et où le facteur (1 + z) prend en
compte la dilatation cosmologique des temps. En combinant ces deux équations, on
trouve
vt
(1 + z)2
a0 χ1 (z) =
Å
σT 4
φ
ã1/2
.
(5.142)
5.8
L’horizon pour ΩM = ΩT > 1 est donné par
a0 χhor = H0−1
1
T
Y
L
PO
ÉC
E
L
O
(ΩT −1)/ΩT
0
1/2
a2 [ΩT a−3 + (1 − ΩT )a−2 ]
0
N
H
EC
da
E
U
IQ
dx
= π/2 − sin−1 [(2 − ΩT )/ΩT ] .
x(1 − x)
La fraction d’univers en deçà de l’horizon est
χhor
sin2 χdχ
Vhor
= [χhor − (1/2) sin 2χhor ] /π .
= 0 π
Vtot
sin2 χdχ
0
(5.143)
(5.144)
(5.145)
Pour ΩT ∼ 1 cela peut s’approximer par
Vhor
16
(ΩT − 1)3/2 [1 + O(ΩT − 1)] .
=
Vtot
3π
(5.146)
U
Q
I
N
L’horizon à amax s’obtient en intégrant de a = 0 à a = amax ou en intégrant de
a = 0 à a = 1 et en prenant ΩT → ∞.
L’âge au moment de l’expansion maximale pour ΩM = ΩT est
amax
tamax =
0
ÉC
H0−1
da
= 1/2
ȧ
ΩT
0
E
L
O
=
ΩT /(ΩT −1)
H
C
TE
a1/2 da
1 − (ΩT − 1)a/ΩT
Y
L
PO
ΩT
π −1
H
.
2 0 (ΩT − 1)3/2
(5.147)
(5.148)
E
370
5.9
ÉC
E
U
IQ
Annexe E. Solutions des exercices
T
Y
L
PO
N
H
EC
L’horizon à l’instant t est donné par
a
da
−1
a0 χhor (t) = H0
.
1/2
2
−3
0 a [ΩM a
+ (1 − ΩT )a−2 + ΩΛ ]
E
L
O
(5.149)
L’intégrale converge évidemment pour a → ∞ si et seulement si ΩΛ > 0.
5.10
Pour un univers avec ΩT = ΩM < 1 on a
da
H0−1 1
lim χ1 (z) =
.
z→∞
2
−3
a0 0 a [ΩT a + (1 − ΩT )a−2 ]1/2
En utilisant a0 = H0−1 /(1 − ΩT )1/2 on trouve
T
Y
L
PO
z→∞
ÉC
N
H
EC
(2−ΩT )/ΩT
lim χ1 (z) =
1
dx
√
x2 − 1
(5.150)
E
U
IQ
ñ
ô
√
2 − ΩT + 2 1 − ΩT
= ln
,
ΩT
E
L
O
(5.151)
ce qui implique
lim r1 (z) = sinh χ =
z→∞
√
2 1 − ΩT
,
ΩT
(5.152)
qui implique à son tour
lim dA (z) =
z→∞
2H0−1
a0 r
=
.
1+z
ΩT z
(5.153)
5.11
Pour ΩT = 1 avec ΩΛ ΩM , l’équation de Friedmann est
ï
ò
1/2
ȧ
ΩΛ 3
= H0 ΩM â−3 + ΩΛ
∼ H0 ΩM â−3/2 1 +
â .
a
2ΩM
Cela donne
T
Y
POL
H
C
E
ï
ò
ΩΛ
2H −1
lim a0 r1 (z) = √ 0
1−
,
z→∞
14ΩM
ΩM
ÉC
E
L
O
avec dA (z) = a0 r1 /(1 + z).
U
Q
I
N
(5.154)
(5.155)
E
T
Y
L
PO
N
H
EC
E
U
IQ
371
En supposant que l’univers est dominé par la matière à la recombinaison avec
H 2 = H02 ΩM â−3
rec , l’angle de Hubble est
ï
ò
1
ΩΛ
θH ∼ √
1−
.
(5.156)
14ΩM
2 1+z
ÉC
E
L
O
Le facteur (1/14) rend le résultat assez insensible aux valeurs relatives de ΩM et ΩΛ
pour ΩM = 0.
5.12
L’absorption par la matière interstellaire ne résoudrait pas le paradoxe d’Olbers car
la matière se chauﬀerait jusqu’à atteindre une température à laquelle elle rayonnerait
des photons du corps noir avec un taux égal au taux absorbé de lumière stellaire.
Les calculs modernes donnent un ﬂux par unité d’angle solide de
2
a(t1 )
r1 dχ1
n0 L t0
dφ
= n0 a30 L
=
dt1
2
dΩ
4πdL
4π 0
a0
=
LY T
n0 L
4π
O
P
E
L
ÉCO
a0
0
N
H
EC
E
U
IQ
da
,
a0 (ȧ/a)
(5.157)
où nous avons utilisé dL = a0 r1 (1 + z) et dχ = dt/a. En utilisant l’équation de
Friedmann pour évaluer ȧ/a on trouve
n0 Lt0
dφ
= (3/5)
dΩ
4π
t0 = (2/3)H0−1
dφ
n0 Lt0
= (1/2)
dΩ
4π
t0 = H0−1
ΩM = ΩT = 1
(5.158)
ΩM = ΩT = 0 .
(5.159)
Dans les deux cas le calcul exact n’ajoute que des facteurs numériques au résultat naïf
que l’on obtient en supposant que les étoiles ont brûlé pendant un temps t0 . Le fait
que les facteurs soient inférieurs à un est dû au redshift. Dans le modèle inﬂationnaire,
on trouve
Å
ã
ainf 4
.
(5.160)
ρ(a0 ) = ρV
a0
On voit que l’énergie décroît en a−4 , comme prévu.
5.13
La probabilité de diﬀusion est
1
P = cH0−1 ne (t0 )σT
ÉC
E
L
O
Y
L
PO
1/(1+z) a4
[ΩM
a−3
H
C
TE
U
Q
I
N
da
1/2
+ ΩΛ + (1 − ΩT )a−2 ]
E
372
E
U
IQ
Annexe E. Solutions des exercices
N
H
EC
î
ó
= 1.2 × 10−3 (1 + z)3/2 − 1 ,
T
Y
L
PO
(5.161)
pour ΩM = ΩT = 1.
Pour z = 5, cela donne P ∼ 10−2 . Par conséquent la diﬀusion Compton n’interfère
pas avec l’observation d’objets de grand redshift.
ÉC
E
L
O
5.14
L’équation (3.86) est équivalente à
dχ = a0 v
da
,
a2 ȧ
(5.162)
si bien que la galaxie la plus lointaine qui puisse être visitée a une coordonnée
∞
dâ
−1
a 0 χ = H0 v
.
(5.163)
1/2
3
−3
â [ΩM â + (1 − ΩT )â−2 + ΩΛ ]
1
N
H
EC
E
U
IQ
Pour ΩM = ΩT = 1, on obtient a0 χ = 2H0−1 v, pour ΩT = ΩM = 0, a0 χ =
et pour ΩT = ΩΛ = 1 a0 χ = H0−1 v/2.
H0−1 v,
5.15
E
L
O
T
Y
L
PO
La distance parcourue par un photon partant à t0 est donnée par
â
dâ
.
a0 χ = H0−1
1/2
1 â2 [ΩM â−3 + (1 − ΩT )â−2 + ΩΛ ]
ÉC
(5.164)
Dans les cas ΩM = ΩT = 1 et ΩM = ΩT = 1, l’intégrale diverge pour â → ∞ et le
photon peut atteindre la totalité de l’univers. Dans le cas ΩΛ = ΩT = 1, l’intégrale
converge et le photon n’atteint que les galaxies contenues dans un volume comobile
ﬁni. Cela, en raison de l’expansion exponentielle dans un univers dominé par le vide.
Chapitre 6
6.1
U
Q
I
N
Il est important de factoriser les paramètres physiques, par exemple :
4πp3 dp
gT 4 ∞
x3 dx
g
=
.
ρ(T, µ = 0) =
(2π)3
exp(p/T ) ± 1
2π 2 0 exp(x) ± 1
H
C
TE
(5.165)
Les intégrales ne donnent que les facteurs numériques de la table 1.
Pour un gaz neutre relativiste d’électrons et de positrons, l’énergie potentielle par
particule est de l’ordre de α ∼ 1/137 multiplié par l’énergie cinétique par particule.
En bon approximation le gaz devrait être « parfait ».
L’asymétrie particules-antiparticules pour un gaz relativiste en équilibre thermique
est de l’ordre de (n − n̄)/n ∼ µ/T .
ÉC
E
L
O
Y
L
PO
E
6.2
T
Y
L
PO
N
H
EC
E
U
IQ
373
L’énergie, l’entropie et le nombre de particules dans un volume V sont donnés par
∂ρ
∂ρ
dT + V
dµ
(5.166)
E = V ρ(T, µ)
⇒ dE = ρdV + V
∂T
∂µ
ÉC
E
L
O
S = V s(T, µ)
⇒ dS = sdV + V
⇒ dN = ndV + V
N = V n(T, µ)
∂s
∂s
dT + V
dµ
∂T
∂µ
(5.167)
∂n
∂n
dT + V
dµ .
∂T
∂µ
(5.168)
D’un autre côté, la variation d’entropie est donnée par On the other hand, the change
is entropy is given by
dS = dE/T + pdV /T − µdN/T .
En substituant dans (5.166) et (5.168) on obtient
ρ + p − µn
dS =
dV + ( ) dT + ( ) dµ .
T
En comparant avec (5.167) on trouve
ρ + p − µn
.
s(T, µ) =
T
6.3
ÉC
T
Y
L
PO
E
L
O
N
H
EC
E
U
IQ
(5.169)
(5.170)
(5.171)
Les particules massives ont une vitesse qui dépend de l’impulsion, par conséquent
dans la ﬁgure 1.10 le carré de gauche devient un parallélogramme. Puisque le parallélogramme a la même aire que le carré, la densité dans l’espace des phases est
conservée.
Pour la ﬁgure 1.11 il nous faut considérer la trajectoire transformée de Lorentz de
la trajectoire x(t) = vp t + dx :
Å
ãÅ
ã
Å
ã
Å ã
γ βγ
t
γt + βγ(dx + vp t)
t
.
(5.172)
=
=
βγ γ
dx + vp t
βγt + γ(dx + vp t)
dx
En posant t = 0 on obtient le temps correspondant dans le référentiel non primé :
t =
−βdx
,
1 + βvp
dont on peut calculer dx
dx =
dx
.
γ(1 + βvp )
Y
L
PO
En transformant le quadrivecteur impulsion, on obtient
ÉC
E
L
O
dp = γ(1 + βvp )dp .
Il s’ensuit que dxdp = dx dp .
U
Q
I
N
(5.173)
H
C
TE
(5.174)
(5.175)
E
374
6.4
T
Y
L
PO
N
H
EC
Le nombre d’interactions subsistantes est
∞
∞
Γ(t)dt =
Γ
ÉC
E
U
IQ
Annexe E. Solutions des exercices
E
L
O
t1
a1
da
.
a(ȧ/a)
(5.176)
Pour obtenir une réponse rapide, on peut évaluer ȧ/a avec une équation de Friedmann
normalisée à a1 , par exemple
ñ
ô1/2
Å ã−4
ȧ
a
= H1 ΩR (a1 )
+ .....
.
a
a1
(5.177)
En reportant cela dans l’intégrale, on trouve que le nombre d’interactions est simplement Γ(t1 )H1−1 fois un facteur numérique de l’ordre de l’unité. Puisque Γ(t1 )H1−1 1,
cela prouve la conjecture.
6.5
T
Y
L
PO
N
H
EC
E
U
IQ
Numériquement, le taux de diﬀusion des photons (toujours dominé par la diﬀusion
Compton) est égal au taux d’expansion à T ∼ 0.236 eV. Le taux de recombinaison
est égal au taux d’expansion à T ∼ 0.215 eV. Un fraction de ∼ 3 × 10−5 des électrons
restent libres. Des calculs plus réalistes incluant tous les états de l’atome d’hydrogène
donne un temps de recombinaison de T ∼ 0.26 eV.
6.6
ÉC
E
L
O
L’annihilation a lieu à T ∼ 10 keV. Un photon d’énergie E = 510 keV a besoin
d’environ 10 collisions pour atteindre une énergie thermique de E ∼ 30 keV. Le temps
pour cela, ∼ 10(ne σT c)−1 , est bien inférieur au temps de Hubble à cette époque.
6.7
Le taux d’annihilation pour des positrons reste supérieur au taux d’expansion
pendant une partie appréciable de l’époque de la matière :
ne σv = ne (t0 )â−3
πα2
(c)2 c ∼ 5 × 10−14 an â−3 ,
m2e c4
H
C
TE
U
Q
I
N
(5.178)
qui est plus grand que le taux d’expansion pour â < 10−2 . Tant que le taux d’annihilation est supérieur au taux d’expansion, on a comme solution de l’équation de
Boltzmann
E
L
O
ne+ ∼
ÉC
Y
L
PO
ne+ (T )ne− (T )
∼ η −1 m3e exp(−2me /T ) .
ne−
(5.179)
E
Pour â ∼ 10−2 cela donne
T
Y
L
PO
N
H
EC
E
U
IQ
ne+ ∼ nγ 10−10 .
E
L
O
7
375
(5.180)
Puisqu’il n’y a que ∼ 1087 photons à l’intérieur de notre horizon, cela signiﬁe qu’il est
très improbable qu’il y ait des positrons subsistants.
ÉC
6.8
La masse minimum est de l’ordre de (mW /α) mW /mpl .
6.9
Le nombre baryonique produit dans une désintégration de X est (2/3)r − (1/3)r =
r − 1/3 alors que dans une désintégration de X̄ il est de −r̄ + 1/3.
L’excédent de baryons après les désintégrations est
nb − nb̄ = nX (r − r̄) .
C
E
T
LY
HN
E
U
IQ
L’asymétrie relative immédiatement après les désintégrations est
ï
ò
nb − nb̄
nX
=
(r − r̄) .
nγ
nγ
t1
ÉC
E
L
O
PO
(5.181)
(5.182)
En supposant une expansion adiabatique après les désintégrations, l’asymétrie actuelle
est
ï
ï
ò
ò
nb − nb̄
g(t0 )
nb − nb̄
.
(5.183)
=
nγ
n
γ
t0
t1 g(t1 )
On dit qu’un réaction viole l’invariance par conjugaison de charge « C » si l’« antiréaction » où toutes les particules sont remplacées par leurs antiparticules ne se
produit pas avec le même taux que la réaction originale.
On dit qu’un réaction viole l’invariance par parité « P » si la réaction vue dans
un miroir ne se produit pas avec le même taux que la réaction originale. (À proprement parler, l’opération P renverse toutes les coordonnées alors que la réﬂexion par
un miroir ne renverse que la coordonnée perpendiculaire au miroir. Toutefois, une
réﬂexion dans un miroir suivie d’une rotation dans le plan du miroir peut renverser
les 3 coordonnées d’espace. La réﬂexion dans un miroir est donc équivalente à P s’il
y a invariance par rotation.)
Enﬁn, une réaction viole « CP » si le processus vu dans un miroir, toutes les
particules étant changées en leurs antiparticules, ne se produit pas avec le même taux
que la réaction originale.
Considérons la réaction
ÉC
E
L
O
X → d̄e+
Y
L
PO
H
C
TE
branching ratio = 1 − r .
U
Q
I
N
(5.184)
E
376
ÉC
E
U
IQ
Annexe E. Solutions des exercices
E
L
O
T
Y
L
PO
N
H
EC
e−
e+
−
X
X
−
d
d
T
Y
L
PO
N
H
EC
E
U
IQ
Fig. E.2: Les désintégrations X → d̄e+ et l’antiréaction X̄ → de− vues dans un miroir.
E
L
O
L’antiréaction voit les orientations relatives des impulsions et des spins renversées. Si, pour
toute orientation des spins, la première réaction se produit avec le même taux que la réaction
transformée, (invariance CP), alors le rapport de branchement moyenné sur les spins pour
X → d̄e+ doit être le même que celui de X̄ → de− .
ÉC
La réaction transformée par C est
X̄ → de−
branching ratio = 1 − r̄ .
(5.185)
Si cette réaction a le même taux que (5.184), c’est-à-dire si C n’est pas violé, alors on
doit avoir r = r̄.
La réaction (5.184) vue dans un miroir avec les particules changées en leurs antiparticules est montrée dans la ﬁgure E.2. La réaction transformée a les orientations
des spins et des impulsions inversées.
Si la réaction transformée se produit avec le même taux que la réaction originale
pour toute combinaison des spins, c’est-à-dire si CP n’est pas violé, alors r = r̄ après
avoir moyenné sur les états de spins possibles.
Par exemple, dans la désintégration du neutron, n → pe− ν̄e , l’hélicité (
p · s) du ν̄
est opposée à l’hélicité du ν produit dans la désintégration de l’antineutron. Puisque
CP est conservé en bonne approximation, les taux sont les mêmes.
Une réaction viole « CPT » si le ﬁlm du processus vu dans un miroir en remplaçant
les particules par les antiparticules, projeté à l’envers ne se passe pas avec le même
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
ÉC
E
L
O
T
Y
L
PO
N
H
EC
e+
e+
ÉC
x
E
L
O
E
U
IQ
377
e−
−
−
d
N
H
EC
−
−
T
Y
L
PO
d
x
e
E
U
IQ
d
d
Fig. E.3: La réaction d̄e+ → d̄e+ et l’antiréaction vue dans un miroir, le ﬁlm étant projeté
à l’envers. L’antiréaction apparaît comme de− → de− . Les deux réactions se passent par
formation résonante de X ou de X̄. Si les sections eﬃcaces des deux processus sont égales
(invariance CPT), les masses et largeurs totales (durées de vie) de X et X̄ doivent être égales.
ÉC
E
L
O
Y
L
PO
H
C
TE
U
Q
I
N
E
378
E
U
IQ
Annexe E. Solutions des exercices
T
Y
L
PO
N
H
EC
taux que la réaction originale. La ﬁgure E.3 montre la réaction
E
L
O
d̄e+ → d̄e+ ,
(5.186)
de− → de− .
(5.187)
et sa transformée par CPT
ÉC
Les réactions vont avoir un pic de résonance à une énergie dans le centre de
masse égale à mX pour la première et à mX̄ pour la seconde. Si l’invariance CPT est
respectée, la section eﬃcace de la première réaction doit être la même que celle de la
seconde. Cela impliquerait que les masses et largeurs totales (durées de vie) de X et
X̄ sont égales.
6.10
Le taux par neutron de np →2 Hγ est
np σv ∼ ηnγ × 7 × 10
−26
LY T
−1
3
m sec
O
P
E
L
ÉCO
N
H
EC
∼ 2 × 10
12
sec
−1
Å
E
U
IQ
T
1 MeV
ã3
,
(5.188)
alors que le taux d’expansion à l’époque considérée est
H ∼ 0.6 sec−1
Å
T
1 MeV
ã2
.
(5.189)
À T = 60 keV il faut que η > 4 × 10−12 pour avoir Γ > H.
L’équation de Saha se déduit de l’expression des potentiels chimique de la table 1.
En utilisant np ∼ ηnγ on trouve
n2
∼
nn
Å
T
mp
ã3/2
η exp(B/T ) ,
(5.190)
qui demeure petit jusqu’à T ∼ 60 keV.
6.11
H
C
TE
U
Q
I
N
E
La durée de la période de désintégration du neutron se calcule en intégrant l’équation de Friedmann equation. Dans l’approximation d’une expansion adiabatique, gs T 3 a3 =
constante, l’équation de Friedmann equation se réduit à
−
ÉC
1/3
Y
L
PO
dgs T
=
1/3
gs T dt
1
E
L
O
Å
8πGgE (T )π 2 T 4
3 × 30
ã1/2
.
(5.191)
Cette équation peu s’intégrer numériquement en utilisant le g(T ) de la ﬁgure 6.1.
T
Y
L
PO
N
H
EC
E
U
IQ
Dans l’approximation g = constante, on a
60 keV
dt ∼ 0.5H(60 keV)−1 ∼ 3min .
E
L
O
379
(5.192)
T =800 keV
L’entropie créée par la désintégration du neutron est régie par l’équation
µi
d(ni a3 ) ,
dsa3 =
(5.193)
T
i
ÉC
où la somme porte sur toutes les espèces. Pour des particules non-relativistes, le
potentiel chimique est
mi
ni
µi
=
+ ln
T
T
2(mi T /2π)3/2
=
mi
+ ln ni /nγ + (3/2) ln T /mi + constant .
T
N
H
EC
E
U
IQ
(5.194)
Pour les désintégrations de neutrons, nous tenons compte du changement de nombre
de neutrons, de protons et d’électrons (en supposant que le potentiel chimique des
neutrinos est nul) pour trouver
E
L
O
T
Y
L
PO
nγ
mn − mp − me
nn
3 me
dsa3
− ln
+ 0.67 .
= −
− ln
− ln
dnn a3
T
ne
np
2
T
ÉC
Si les désintégrations se produisent vers T ∼ 100 keV tous les termes importants
du membre de droite sont d’ordre ∼ 10 et l’entropie créée est de l’ordre de
∆s
∆nn
∼ 10
∼ η.
s
s
(5.195)
Dans la phase de contraction d’un univers fermé, aucun neutron n’est présent
initialement et la désintégration inverse pe− ν̄e → n est très peu probable. Les neutrons apparaissent seulement lorsque la température atteint ∼ 800 keV et qu’ils sont
produits par les réactions pe− → nνe et pν̄e → e+ n.
6.12
U
Q
I
N
La température de gel est proportionnelle à g 1/6 et la sensibilité du rapport
neutron-proton au nombre d’espèces de neutrinos, au moment du gel est
Y
L
PO
∆(n/p)
∆2Nν
∼ (1/6)
.
n/p
g
E
L
O
H
C
TE
(5.196)
Ajouter une espèce supplémentaire de neurinos augmenterait de 10% le rapport n/p,
si bien qu’avec cette précision, il doit être possible de trouver une limite sur le nombre
de neutrinos supplémentaires d’à peu près 2.
ÉC
E
380
E
U
IQ
Annexe E. Solutions des exercices
Chapitre 7
T
Y
L
PO
7.2
E
L
O
N
H
EC
En divisant (7.17) par (7.15), on trouve
ÉC
1/2
dac
a1/2 Hc1 Ωc1
= 1/2
da
H1
ac
Å
ã
Ωc1 − 1
1−
ã .
2Ωc1
(5.197)
1/2
En prenant ac = a(1 − a) et Hc1 Ωc1 /H1 ∼ 1 on trouve
∼ (2/5)
Ωc1 − 1
.
2Ωc1
(5.198)
7.3
N
H
EC
E
U
IQ
Un photon de trajectoire r(t) = v t + dr a une trajectoire transformée donnée par
Ü
γ
βγ
0
0
βγ
γ
0
0
ÉC
0
0
1
0
0
0
0
1
êÜ
E
L
O
ê
Ü
T
Y
L
PO
t
dz + vz t
dy + vy t
dx + vx t
=
γt(1 + βvz ) + βγdz
γt(β + vz ) + γdz
dy + vy t
dx + vx t
ê
. (5.199)
En posant t = 0 on a le temps correspondant dans le référentiel non-primé :
−βdz
,
1 + βvz
(5.200)
dz
γ(1 + βvz )
(5.201)
dy = dy − vy βdz
(5.202)
t =
dont nous pouvons calculer dr
dz =
dx = dx − vx βdz ,
Y
L
PO
H
C
TE
U
Q
I
N
(5.203)
ce qui correspond au cube de la ﬁgure 7.13 de volume dxdydz/[γ(1 + βvz )]. En transformant le quadrivecteur impulsion on trouve
E
L
O
dpz
ÉC
= γ(1 + βvz )dpz ,
et dpy = dpy et dpx = dpx . Il s’ensuit que d3rd3 p = d3r d3 p .
(5.204)
E
7.5
T
Y
L
PO
N
H
EC
E
U
IQ
381
Pour des photons pγ = ργ /3 par conséquent
E
L
O
dργ V = −pγ dV
ÉC
⇒
dργ = −(4/3)ργ dV /V .
(5.205)
Pour les baryons, la pression s’annule et
dρb V = −ρb dV 0
⇒
dρb = −ρb dV /V .
(5.206)
dρ = −(4ργ /3 + ρb )dV /V = (4ργ /3 + ρb )dργ /(4ργ /3) .
(5.207)
En ajoutant ces deux équations, on obtient
E
U
IQ
En utilisant dp = ργ /3 dans cette équation, on trouve le résultat voulu.
dp
1
= c2s = (1/3)
.
dρ
1 + 3ρb /(4ργ )
7.6
T
Y
L
PO
N
H
EC
(5.208)
L’univers doit être réionisé avant â ∼ 1/30 pour avoir une profondeur optique
unité. Si c’est le cas, entre la recombinaison et la réionisation, les photons parcourent
une distance de l’ordre de la distance de Hubble distance à la réionisation. Les photons
diﬀusés dans une ligne de visée donnée proviendront donc de la recombinaison dans
une région d’échelle angulaire donnée par la distance de Hubble à la réionisation.
ÉC
E
L
O
7.7
En suivant le même raisonnement que dans le texte pour arriver à la formule
(7.51), on trouve
dk
2
|U (kR)|2 ∆2k ,
(5.209)
(MR − (1/8)M2R ) =
k
où
U (kR) = W (kR) − W (2kR) .
La fonction U (kR) a un pic vers k =∼ 2.2/R
7.8
Y
L
PO
H
C
TE
U
Q
I
N
(5.210)
Le mode le plus long qui n’a jamais été hors du rayon de Hubble a
ÉC
E
L
O
λ(a0 )
a1
< dH (a1 ) ,
a0
(5.211)
E
382
E
U
IQ
Annexe E. Solutions des exercices
N
H
EC
où a1 se rapporte à la ﬁn de l’inﬂation. En prenant a1 /a0 ∼ 1015 GeV/10−4eV et en
utilisant l’équation de Friedmann, cela donne
E
L
O
T
Y
L
PO
λ(a0 ) ∼ 10−26 H0−1 ∼ 1 m .
(5.212)
Les modes de longueur d’onde plus courte que cette valeur ne devraient pas avoir un
spectre invariant d’échelle.
ÉC
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
E
N
H
EC
T
Y
L
PO
E
U
IQ
E
L
CO F
ÉAnnexe
Formules et nombres utiles
– équation de Friedmann pour le facteur d’échelle a(t) :
N
H
EC
Å ã2
ȧ
8πGρ
+ H02 (1 − ΩT ) â−2 ,
=
a
3
T
Y
L
PO
E
U
IQ
(6.1)
où ΩT est la densité totale actuelle divisée par la densité critique
ÉC
et où
E
L
O
ΩT =
ρ(a0 )
,
3H02 /8πG
H −1
a0 = 0
|1 − ΩT |
(6.2)
â(t) =
a(t)
.
a0
(6.3)
– Équation de Friedmann pour l’époque actuelle :
1/2
ȧ
= H0 ΩR â−4 + ΩM â−3 + ΩΛ + (1 − ΩT )â−2
,
a
(6.4)
où ΩR , ΩM , et ΩΛ sont les contributions actuelles de matière relativiste, de
matière non-relativiste et d’énergie du vide :
H
C
TE
ΩT = ΩR + ΩM + ΩΛ .
Y
L
PO
U
Q
I
N
(6.5)
– Équation de Friedmann pendant l’époque de rayonnement :
ȧ
=
a
Å
8πG
π2
gE (T ) T 4
3
30
ÉC
ã1/2
E
L
O
∼ 0.65 s−1
Å
T
1 MeV
où gE est le nombre eﬀectif d’états de spin (Fig. 6.1).
383
ã2 gE 1/2
10
(6.6)
E
384
E
U
IQ
Annexe F. Formules et nombres utiles
T
Y
L
PO
N
H
EC
– Coordonnée radiale χ d’un objet de redshift z :
a0
da
χ(z) =
2
a0 /(1+z) a (ȧ/a)
ÉC
E
L
O
H −1
= 0
a0
1
(6.7)
dâ
(1+z)−1
â2
(ΩR
â−4
+ ΩM
â−3
1/2
+ ΩΛ + (1 − ΩT )â−2 )
.
– χ(z) pour z 1
ò
ï
1 + q0
z + ..... .
a0 χ1 (z) = a0 r1 (z) = H0−1 z 1 −
2
– Distance de luminosité et distances angulaires :
dL (z) = a0 r(z)(1 + z)
C
E
T
LY
HN
E
U
IQ
dA (z) = a0 r(z)/(1 + z) ,
O
P
E
L
ÉCO
où la coordonnée radiale r est
r =
ÉC
sin χ = χ − χ3 /6 + .....
χ
sinh χ = χ + χ3 /6 + .....
E
L
O
Y
L
PO
(6.8)
(6.9)
(6.10)
ΩT > 1
ΩT = 1 .
ΩT < 1
H
C
TE
(6.11)
U
Q
I
N
E
ÉC
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
385
Tab. F.1 : Constantes physiques, tirées de [21].
quantité
symbole
valeur
vitesse de la lumière dans le vide
constante de Planck
constante de conversion
constante de conversion
c
c
2πc
2.99 792 458 × 108 m s−1
1.054 571 596(82) × 10−34 J s
1.97 326 960 2(77) × 10−7 eV m
1.24 × 103 eV nm
constante de structure ﬁne
section eﬃcace Thomson
constante de Newton
masse de Planck
constante de Fermi
α
σT
GN (=
G)
mpl = c/G
GF /(c)3
1/137.035 999 76(50)
0.665 245 854(15) × 10−28 m2
6.673(10) × 10−11 m3 kg−1 s−2
1.221 0(9) × 1019 GeV/c2
1.166 39(1) × 10−5 GeV−2
masse de l’électron
masse du proton
neutron-proton ∆m
masse du deutéron
me
mp
m n − mp
md
0.510 998 902(21) MeV/c2
938.271 998(38) MeV/c2
1.293 318(9) MeV/c2
1875.612 762(75) MeV/c2
constante de Boltzmann
k
1.380 650 3(24) × 10−23 J Kelvin−1
8.617 342(15) × 10−5 eV Kelvin−1
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
E
386
E
U
IQ
Annexe F. Formules et nombres utiles
T
Y
L
PO
N
H
EC
Tab. F.2: Quantités astrophysiques et cosmologiques, tirées de [21]. H0 et toutes les densités
correspondent à l’époque actuelle.
E
L
O
quantité
symbole
valeur
unité astronomique
parsec
UA
pc
solar masse
M
luminosité solaire
L
rayon équatorial solaire
R
1.495 978 706 60(20) × 1011 m
3.085 677 580 7(4) × 1016 m
=3.262... années lumière
1.988 9(30) × 1030 kg
= 1.189 × 1057 mp
3.846(8) × 1026 W s−1
2.40 × 1045 eV s−1
6.961 × 108 m
ÉC
taux d’expansion de Hubble
H0
N
H
EC
E
U
IQ
−1
−1
densité critique
ρc = 3H02 /8πG
température du CBR
Tγ
kTγ
ργ
Ωγ
nγ
nν = (3/11)nγ
70h70 km s Mpc
100h km s−1 Mpc−1
h70 = 1.0 ± 0.15
h = 0.7 ± 0.1
10
1.40 h−1
an
70 × 10
−1
4.41 h70 × 1017 s
4280 h−1
70 Mpc
26
1.32 h−1
70 × 10 m
2
−26
0.92h70 10
kg m−3
2
9
5.16h70 10 eV/c2 m−3
1.36h270 1011 M Mpc−3
2.725 ± 0.001 Kelvin
(2.348 ± 0.002) × 10−4 eV
0.26038 (Tγ /2.725)4 eV cm−3
−5
5.06 h−2
70 × 10
410.50 (Tγ /2.725)3 cm−3
111.95 (Tγ /2.725)3 cm−3
nb = ηnγ
Ωb
ΩM
ΩΛ
∼ 5 × 10−10 nγ ∼ 0.2 m−3
∼ 0.04 h−2
70
∼ 0.3
∼ 0.7
temps de Hubble
E
L
O
distance de Hubble
ÉC
T
Y
L
PO
densité d’énergie du CBR
nombre volumique du CBR
neutrinos (+antineutrinos)
nombre volumique par espèce
baryons
nombre volumique
densité
matière non-relativiste
énergie du vide
égalité matière-rayonnement
facteur d’échelle
température du CBR
recombinaison
facteur d’échelle
température du CBR
ÉC
E
L
O
tH = H0−1
dH = cH0−1
Y
L
PO
âeq = 1.68Ωγ /ΩM
kTeq
ârec
kTrec
H
C
TE
U
Q
I
N
0.85 × 10−4 /(ΩM h270 )
2.8 ΩM h270 eV
1/1100
0.26 eV
E
E
L
O
T
Y
L
PO
N
H
EC
E
U
IQ
C
ÉBibliographie
[1] Les références [2] à [20] concernent des ouvrages de référence en
astronomie, en astrophysique, en relativité générale, en physique des particules
élémentaires et en cosmologie. La référence [21] est la source de la
plupart des valeurs numériques utiliséees dans ce texte.
Les preprints nommés « astro-ph » ou « hep » peuvent être trouvés
(par exemple) à :
T
Y
L
PO
N
H
EC
E
U
IQ
http ://xxx.lanl.gov/ ;
http :babbage.sissa.it/ ; http ://xxx.lpthe.jussieu.fr/
ÉC
E
L
O
[2] J. Binney et M. Merriﬁeld : Galactic Astronomy (Princeton
University Press, Princeton 1998)
[3] J. Binney et S. Tremaine : Galactic Dynamics
(Princeton University Press, Princeton, 1987)
[4] G.S. Bisnovatyi-Kogan : Stellar Physics (Springer, Berlin, 1999)
[5] M. Harwit : Astrophysical Concepts (Springer, Berlin, 1998)
[6] P. Lena, F. Lebrun, et F. Mignard : Observational Astrophysics
(Springer, Berlin, 1998)
[7] S. Weinberg Gravitation and Cosmology (Wiley, New York,
1972)
[8] C.W. Misner, K.S. Thorne et J.A. Wheeler : Gravitation
(Freeman, New York, 1973)
H
C
TE
U
Q
I
N
[9] F. Halzen et A.D. Martin : Quarks and Leptons (Wiley,
New York, 1984)
Y
L
PO
[10] W. Greiner et B. M¸ller : Gauge Theory of Weak Interactions
(Springer, Berlin, 2000)
ÉC
E
L
O
[11] U. Mosel : Fields, Symmetries, and Quarks (Springer, Berlin, 1999)
387
E
388
E
U
IQ
Bibliographie
T
Y
L
PO
N
H
EC
[12] Q. Ho-Kim et X.-Y. Pham : Elementary Particles and Their Interactions
(Springer, Berlin, 1998)
[13] E. W. Kolb et M.S. Turner : The Early Universe (Addison-Wesley,
Redwood City, 1990)
ÉC
E
L
O
[14] T. Padmanabhan : Structure Formation in the Universe
(Cambridge University Press, Cambridge, 1993)
[15] P.J.E. Peebles : Principles of Physical Cosmology
(Princeton University Press, Princeton, 1993)
[16] P. Coles : Cosmology : the Formation and Evolution of Cosmic Structure
(Wiley, New York, 1995)
[17] J.A. Peacock : Cosmological Physics (Cambridge
University Press, Cambridge, 1999)
E
U
IQ
[18] F. Combes, P. Boisse, A. Mazure, et A. Blanchard : Galaxies and Cosmology
(Springer, Berlin, 1995)
T
Y
L
PO
N
H
EC
[19] M.S. Longair : Galaxy Formation (Springer, Berlin, 1998)
[20] G. Borner : The Early Universe, Facts and Fiction (Springer,
Berlin, 1993)
E
L
O
[21] Particle Data Group : Eur. Phys. J. C 15, 1 (2000)
ÉC
[22] J. Mather et al. : Ap. J. 512, 511 (1999)
[23] Y. Fukuda et al. : Phys. Rev. Lett. 81, 1562 (1998)
[24] D. Tytler et al. : Physica Scripta T85, 12 (2000) et
astro-ph/0001318
[25] A.H. Jaﬀe et al. : astro-ph/000733,
Phys. Rev. Lett. 86, 3475 (2001) ; des résultats plus récents
de Boomerang se trou !vent dans astro-ph/0105296
[26] S. Perlmutter et al. : Ap. J. 517, 565 (1999)
[27] B. Schmidt et al. : Ap. J. 507, 46 (1998)
[28] http ://www.eso.org
[29] http ://space.gsfc.nasa.gov/astro/cobe
H
C
TE
[30] B.F. Madore et al. : Ap. J. 515, 29-41 (1999)
Y
L
PO
U
Q
I
N
[31] R. Cen et J.P. Ostriker : Ap. J. 514, 1 (1999)
[32] Combes, F. et D. Pfenniger : Astron. Astrophy. V, 453 (1997) ;
de Paolis et al. Ap. J. 510L, 103 (1999) ; de Paolis et al. Phys. Rev. Lett.
74, 14 (1995)
ÉC
E
L
O
[33] A.G. Cohen, A. De Rujula et S.L. Glashow : Ap. J. 495, 539 (1998)
E
Bibliographie
T
Y
L
PO
N
H
EC
E
U
IQ
389
[34] K. Griest et J. Silk : Nature 343, 26 (1990)
[35] B. Carr et C Goymer : astro-ph/0003027
[36] J.N. Bahcall et al. : Phys. Rev D 58 096016 (1998)
E
L
O
[37] P. Smith et J. Lewin : Phys. Rep. 187, 203 (1990)
ÉC
[38] L. R. Wang, R. R. Caldwell, J. P. Ostriker et P. J.
Steinhardt : Ap. J. 530, 17 (2000) ; R.R. Caldwell, R. Dave et P.J.
Steinhardt, Phys. Rev. Lett. 80, 1582 (1998) ; P. Binétruy :
Int.J.Theor.Phys. 39, 1859 (2000)
[39] R. Srianand, P. Petitjean et C. Ledoux : Nature 408, 931 (2000)
[40] M. Milgrom : Ap. J. 270, 365 (1983)
[41] A. Albrecht : astro-ph/9904185
E
U
IQ
[42] N. Arkani-Hamed et al. : Phys. Rev. Lett. 85, 4434 (2000)
N
H
EC
[43] C. Armendariz-Picon, V. Mukhanov et P. J. Steinhardt : Phys.Rev.Lett.
85, 4438 (2000)
T
Y
L
PO
[44] J.D. Barrow et F.J. Tipler The Anthropic Cosmological Principle
(Oxford University Press, Oxford, 1988) ; C.J. Hogan : Rev.Mod.Phys.
72, 1149 (2000) ;
pour un point de vue contradictoire, voir G.L Kane, M.J. Perry et A.N.
Zytkow astro-ph/0001197
ÉC
E
L
O
[45] S. Weinberg : astro-ph0005265 ; H. Martel, P. R. Shapiro et
S. Weinberg : Ap. J. 492, 29 (1998)
[46] J. Gunn et L. Stryker : Ap. J. Supp. 52, 121 (1983) ;
http ://vizier.u-strasbg.fr/viz-bin/Cat
[47] http//astro.estec.esa.nl/Hipparcos
[48] J. Binney et M. Merriﬁeld : Galactic Astronomy
(Princeton University Press, Princeton 1998) p. 137
[49] Holtzman, J. A. et al. : A. J. 118, 2262 (1999)
[50] Girardi, L., M. A. T. Groenewegen, A. Weiss et
M. Salaris : M.N.R.A.S. V, 149 (1998) ; L. Girardi et M. Salaris :
astro-ph/0007343
[51] B. Gibson : astro-ph/9910574
[52] F. Pont : astro-ph/9812074
Y
L
PO
H
C
TE
[53] A. Udalski et al. : Acta Astronomica 49, 201 (1999)
[54] N. Suntzeﬀ et al. : A. J. 117, 1175 (1999)
E
L
O
[55] See e.g. Osmer, P. S. : astro-ph/9901238
ÉC
[56] S. Shectman et al. : Ap. J. 470, 172 (1996)
U
Q
I
N
E
390
E
U
IQ
Bibliographie
T
Y
L
PO
N
H
EC
[57] H. Lin et al. : Ap. J. 464, 60(1996)
[58] K. Begeman : Astron. Astrophy. 223, 47 (1989)
[59] N. Bahcall : American Astronomical Society Meeting
194, 3002 (1999) et astro-ph/9804082
ÉC
E
L
O
[60] J. Mohr et al. : astro-ph/0004244
[61] S. Schindler : astro-ph/9811470 et S. Schindler et al. : Astron. Astrophy.
317, 646 (1997)
[62] J. Ellis et al. : Phys.Rev. D 62, 075010 (2000)
[63] M.W. Goodman et E. Witten : Phys. Rev. D 31, 3059 (1985).
[64] K. Freese, J. Freedman et A. Gould : Phys. Rev. D 37, 3388 (1988)
[65] R. Abusaidi et al. : Phys. Rev. Lett. 84, 5699 (2000)
[66] D. Drain et al : Phys. Rep. 307, 297 (1998)
N
H
EC
[67] R. Bernabei et al : Phys. Lett. B 480, 23 (2000)
[68] L. Baudis et al : Phys. Rev. D 59, 022001 (1999)
T
Y
L
PO
E
U
IQ
[69] M. Mori et al. : Phys. Lett. B 270, 89 (1991)
[70] M. Mori, et al. : Phys. Lett. B 289, 463 (1992)
E
L
O
[71] F. Halzen, T. Stelzer et M. Kamionkowski : Phys. Rev.
D45 4439 (1992)
ÉC
[72] Antares Collaboration, http ://antares.in2p3.fr
[73] Amanda Collaboration, http ://amanda.berkeley.edu
[74] H. Cheng : Phys. Rep. 158, 1 (1988)
[75] P. Sikivie : Phys. Rev. Lett. 51, 1415 (1983)
[76] W. Wuensch et al. : Phys. Rev. D 40, 3153 (1988)
[77] C. Hagmann et al. : 1990 Phys. Rev. D 42, 1297 (1990)
[78] C. Hagmann, et al. : Phys. Rev.Lett. 80, 2043 (1998)
[79] B. Carr : Comments Astrophys. 14, 257 (1990)
U
Q
I
N
[80] B.D. Fields, K. Freese et D. S. Graﬀ : Ap. J. 534, 265 (2000)
[81] B. Paczyński : Ap. J. 304, 1 (1986)
[82] K. Griest : Ap. J. 366, 412 (1991)
H
C
TE
[83] C. Alcock et al. : Ap. J. Lett. 499, L9 (1998)
Y
L
PO
[84] C. Alcock et al. : Ap. J. 542, 281 (2000)
[85] T. Lasserre et al. : Astron. Astrophy. 355, L39 (2000)
E
L
O
[86] C. Afonso et al. : Ap. J. 532, 340 (2000)
ÉC
[87] C. Alcock et al. : Ap. J. Lett. 454, L125 (1995)
E
Bibliographie
T
Y
L
PO
N
H
EC
E
U
IQ
391
[88] A.P.S. Crotts et A. B. Tomaney : Ap. J. Lett. 473, L87
(1996) ; R. Ansari et al. : Astron. Astrophy. 324, 843 (1997)
[89] A. Vidal-Madjar et al. : Ap. J. Lett. 538, L77 (2000)
ÉC
E
L
O
[90] P. Salati et al. : Dark matter in astro- and particle physics : (DARK ’96)
editeurs, H.V. Klapdor-Kleingrothaus et al. (World Scientiﬁc, 1997)
[91] R. R. Raﬁkov et B. T. Draine :astro-ph/0006320
[92] H. Tadros, S.J. Warren et P.C.Hewett, astro-ph/0003422
[93] M. Hamuy et al. : A. J. 112, 2398 (1996)
[94] B. Gibson et al. : Ap. J. 529, 723 (2000)
[95] S. Sakai et al. : Ap. J. 529, 698 (2000)
[96] Ekholm,T. et al., Astron. Astrophy. 347, 99 (1999)
[97] L. Ferrarese et al. : Ap. J. 529, 745 (2000)
N
H
EC
[98] Schmidt, B. et al., Ap. J. 432 42 (1994)
E
U
IQ
[99] C. Fassnacht et al. : Ap. J. 527, 498 (1999) ; L. Williams et P. Saha :
A. J. 119, 439 (2000)
T
Y
L
PO
[100] S.T. Myers, J. E. Baker, A. C. S. Readhead, E. M. Leitch
et T. Herbig : Ap. J. 485, 1 (1997)
E
L
O
[101] S.D.M. White, J. F. Navarro, A. E. Evrard et C. S. Frenk : Nature 366,
429 (1993)
ÉC
[102] J. Oukbir et A. Blanchard : Astron. Astrophy. 262, L21 (1992)
[103] J. P. Henry : Ap. J. 534, 565 (2000)
[104] J. Peacock : M.N.R.A.S. 284, 885 (1997)
[105] Aguirre, A. : Ap. J. 525, 583 (1999)
[106] P. de Bernardis et al. : Nature 404, 995 (2000)
[107] S. Hanany et al. : Ap. J. Lett. 545, L5 (2000)
[108] Microwave Anisotropy Probe : http ://map.gsfc.nasa.gov/ ; Planck Surveyor :
http ://sci.esa.int/home/planck/index.cfm
[109] F. C. Durret et al. : Astron. Astrophy. 356, 815 (2000)
[110] A. Bosma : A. J. 86, 12 (1981)
H
C
TE
[111] E. F. Guinan et al. : Ap. J. Lett. 509, L21 (1998)
U
Q
I
N
[112] Nauenberg M. et V. Weisskopf : Am.J.Phys. 46 (1), 23 (1978).
Y
L
PO
[113] J.D. Jackson Classical Electrodynamics (Wiley, New York, 1962)
E
L
O
[114] J.W. Bailey et al. : Phys. Lett. 28B, 287 (1968)
[115] A. Riess et al. : A. J. 114, 722 (1997),
astro-ph/9707260
ÉC
E
392
E
U
IQ
Bibliographie
T
Y
L
PO
N
H
EC
[116] P. Schneider, P., J. Ehlers et E.E. Falco Gravitational Lenses
(Springer, Berlin, 1992)
ÉC
[117] L. Van Waerbeke et al. : Astron. Astrophy. 358, 30 (2000) ; D. Wittman
et al. :
Nature 405, 143 (2000) ; D. Bacon,1), A. Refregier et R. Ellis :
M.N.R.A.S.
318, 625 (2000) ; N. Kaiser, G. Wilson et G. Luppino : astro-ph/0003338
E
L
O
[118] B. Chaboyer : Phys. Rep. 307, 23 (1998)
[119] S. Cassisi, V. Castellani, S. degl’Innocenti, M.
Salaris et A. Weiss : Astron. Astrophy. Supp. 134, 103 (1999)
[120] A. G. Riess : Pub. Ast. Soc. Pac. 112, 1284 (2000)
[121] C.S. Kochanek : Ap. J. 419, 12 (1993) ; D.
Maoz H. Rix : Ap. J. 416, 425 (1993)
[122] A. Loeb : Ap. J. 499, L111 (1998)
N
H
EC
E
U
IQ
[123] A.H. Guth : Phys. Rev. D 23, 347 (1981)
T
Y
L
PO
[124] A.D. Linde : Phys. Lett. 108B, 389 (1982) ; A. Albrecht et
P.J. Steinhardt : Phys. Rev. Lett. 48, 1220 (1982)
E
L
O
[125] A.D. Linde : Phys. Lett. 129B, 177 (1983)
ÉC
[126] J.E. Gunn et B.A. Peterson : Ap. J. 142, 1633 (1965)
[127] J. A. Newman et M. Davis : Ap. J. Lett. 534, L11 (2000)
[128] voir J.J. Sakurai Advanced Quantum Mechanics
(Adison-Wesley, Reading, 1967)
[129] E. Browne et R.B. Firestone : Table of Radioactive Isotopes (Wiley, New
York, 1986)
[130] E. Vangioni-Flam, A. Coc et M. Casse : Astron. Astrophy. 360, 15 (2000)
[131] S. Burles et D. Tytler :Stellar Evolution, Stellar Explosions and Galactic
Chemical Evolution,
Second Oak Ridge Symposium on Atomic and Nuclear Astrophysics
(IOP,Bristol, 1998) et astro-ph/9803071
U
Q
I
N
[132] D. Kirkman D. Tytler, S. Burles, D. Lubin et J. M. O’Meara :
Ap. J. 529, 655 (2000) ; S. Burles et D. Tytler : Ap. J. 507, 732 (1998) ;
S. Burles et D. Tytler : Ap. J. 499, 699 (1998)
Y
L
PO
H
C
TE
[133] J. K. Webb et al. : Nature 388, 250 (1997)
[134] B. D. Fields et K. A. Olive : Ap. J. 506, 177 (1998)
E
L
O
[135] Y. I. Izotov et T. X. Thuan : Ap. J. 500, 188 (1998)
ÉC
[136] S. G. Ryan et al. : Ap. J. 523, 654 (1999)
E
Bibliographie
T
Y
L
PO
N
H
EC
E
U
IQ
393
[137] K. A. Olive, G. Steigman et T. P. Walker : Phys. Rep.
333, 389 (2000)
[138] M. Rauch et al. : Ap. J. 489, 7 (1997)
E
L
O
[139] M. Trodden : Rev. Mod. Phys. 71 1463 (1999)
ÉC
[140] E. W. Kolb et M.S. Turner : op. cit. p. 160
[141] D. Lynden-Bell : M.N.R.A.S. 136, 101 (1967)
[142] C.S. Frenk et al. : astro-ph/0007362
[143] A. Dekel : ASP Conf. Ser. 201 Cosmic Flows Workshop (2000).
astrp-ph/9911501 ; I. Zehavi et A. Dekel : Nature 401, 252 (1999) ;
P.G. Ferreira, R. Juszkiewicz, H. A. Feldman, M. Davis et A. H. Jaﬀe :
Ap. J. Lett. 515, L1 (1999)
[144] The Sloan Digital Sky Survey :
http ://www.sdss.org/ ;
The 2dF Galaxy Redshift Survey :
http ://www.mso.anu.edu.au/2dFGRS/
T
Y
L
PO
N
H
EC
E
U
IQ
[145] J.A. Peacock : Cosmological Physics
(Cambridge University Press, Cambridge, 1999) p. 527 ;
adapted from J.A. Peacock et S.J. Dodds : M.N.R.A.S. 267, 1020 (1994)
E
L
O
[146] C. H. Lineweaver : astro-ph/9609034
ÉC
[147] J. A. Willick : astro-ph/0003232
[148] J.A. Peacock : M.N.R.A.S. 284, 885 (1997)
[149] J.A. Peacock : Cosmological Physics (Cambridge
University Press, Cambridge, 1999) p. 529
[150] J.A. Peacock, ibid p. 532
[151] J. M. Bardeen, P. J. Steinhardt et M.S. Turner :
Phys. Rev. 28, 679 (1983) ; A.H.Guth et S.-Y. Pi : Phys. Rev. Lett
49, 1110 (1982) ; A.A. Starobinskii : Phys. Lett. 117B, 175
(1982) ; S.W. Hawking : Phys. Lett. 115B, 295 (1982)
[152] M. Tegmark et M. J. Rees : Ap. J. 499, 526 (1998)
[153] P.J.E. Peebles : Ap. J. Lett. 263, L1 (1983)
H
C
TE
[154] E. Gawiser et J. Silk : Science 280, 1405 (1998)
U
Q
I
N
[155] N.A.Bahcall, J. P. Ostriker, S. Perlmutter et P.J. Steinhardt : Science
284, 1481 (1999)
Y
L
PO
[156] J. A. Sellwood : Ap. J. Lett. 540, L1 (2000) ; D. N. Spergel et P.J. Steinhardt : Phys. Rev. Lett. 84, 3760 (2000) ; M. Kamionkowski et A.R.
Liddle : Phys. Rev. Lett. 84, 4525 (2000)
ÉC
E
L
O
[157] F. C. van den Bosch et R. A. Swaters : astro-ph/0006048
E
394
E
U
IQ
Bibliographie
T
Y
L
PO
N
H
EC
[158] M. White et W. Hu : Astron. Astrophy. 321, 8 (1997)
[159] C. Bennett et al. : Ap. J. Lett. 464, L1 (1996)
[160] W. Hu, N. Sugiyama, J. Silk : Nature 386, 37 (1997), astro-ph/9604166
ÉC
E
L
O
[161] P.J.E. Peebles : Principles of Physical Cosmology
(Princeton University Press, Princeton, 1993) pp. 290-292
[162] voir, par exemple, T. Padmanabhan : Structure Formation in the Universe
(Cambridge University Press, Cambridge, 1993) p. 222
[163] voir, par exemple, A. Riazuelo, N. Deruelle et P. Peter : Phys.Rev.
D 61, 123504 (2000)
[164] U. Seljak et M. Zaldarriaga : CMBFAST, a Microwave Anisotropy Code,
http ://www.sns.ias.edu/ matiasz/CMBFAST/cmbfast.html
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
E
Index
LE
ÉCO
T
Y
L
PO
ΩCDM , 13, 24
ΩM , 24, 54, 95, 96, 193
de l’âge de l’univers, 189
de la proportion de baryons dans
les amas, 94, 98
du rapport M/L d’un amas, 98
et anisotropies du CBR, 320
et la formation de structures, 45,
95
et la formation des structures, 94
ΩR , 38
et anisotropies du CBR, 320
ΩT , 13, 21, 54, 95
évolution, 44, 208
des anisotropies du CBR, 96, 320
Ωb , 13, 22, 94
et anisotropies du CBR, 320
ΩΛ , 13, 28, 54, 95, 193
de l’âge de l’univers, 189
des supernovae, 96
et anisotropies du CBR, 320
Ωvis , 22
σ8 , 283, 285
t0 , 30
écoulement libre, 265, 268, 304
égalité matière-rayonnement, aeq , 38,
294
époque de la courbure , 43
époque de la matière, 43
époque du rayonnement , 43
époque du vide, 43
équation d’Einstein, 183
équation d’état, 165, 187
équation de Boltzmann, 39
ÉC
E
L
O
ÉC
N
H
EC
équation de Friedmann, 167, 169, 178,
182
équation de Liouville, 39, 227, 258
équation de Saha, 244, 259, 263
équations d’Einstein, 178, 179
équilibre chimique, 220, 232, 233, 239,
241
équilibre cinétique, 219, 261
équilibre thermique, 219, 222, 229, 231
étalonnage des distances, 63
étoiles à neutrons, 64, 83
étoiles variables Céphéides, 63, 65, 67,
69, 71, 74, 90, 98, 99, 103
évolution stellaire, 55
âge de l’univers, 189
T
Y
L
PO
E
L
O
E
U
IQ
N
H
EC
E
U
IQ
distance de luminosité, 193
formation des structures bottom-up, 305
absorption (interstellaire), 58, 342, 343
amas de galaxies, 18, 74, 87, 98
émission de rayons X, 106
évolution, 94
évolution du nombre volumique, 285,
286, 302
dispersion en vitesse, 277, 298
eﬀet SZ, 91, 315
et ﬁlaments, 272
et matière noire chaude, 305
ﬂuctuation du nombre volumique,
270, 282–284
formation, 271
fraction baryonique, 76
lensing gravitationnel par, 91, 144,
146
Y
L
PO
395
H
C
TE
U
Q
I
N
E
396
T
Y
L
PO
lentille gravitationnelle par, 146
proportion de baryons, 94
amas globulaires, 191, 192
amortissement de Silk, 306
antimatière, 252
asymétrie du nombre leptonique, 253
asymétrie particule-antiparticule, 238,
239, 252
axions, 83
ÉC
E
L
O
baryogénèse, 252
big bang, 20
Boomerang, 96, 197, 200, 313, 319
bremsstrahlung, 76, 93, 106–108, 231
champ scalaire, 29, 52, 171, 210
chandelles standard, 63, 64, 67, 90, 194
COBE, 15, 26, 92, 297, 313, 319
comptage du nombre de galaxies, 215
conservation de l’énergie, 157, 165–167
constante cosmologique, 28
constante de Fermi, 339
constante de Hubble H0 , 17, 30, 89
coordonnées comobiles, 115, 121, 123
coordonnées en chute libre, 112, 117,
158, 162
cosmic background radiation (CBR)
anisotropies, 197
courbes de rotation des galaxies, 14,
70, 71, 99, 298
ÉC
E
L
O
E
L
O
N
H
EC
E
U
IQ
ﬁltres, systèmes de , 342
ﬁne-tuning, 51, 209
ﬂots globaux, 287
ﬂuctuations d’iso-courbure, 269, 280,
306, 317, 319
ﬂuctuations de densité adiabatiques, 269
et anisotropies du CBR, 296, 316,
317, 319
fond cosmique de photons (CBR), 25,
92, 97, 218
évolution de la température, 37,
220
anisotropies, 95, 96, 198, 247, 266,
269, 297, 306, 309–319
dipôle, 285
et causalité, 201, 203
et eﬀet SZ , 91
fond cosmique de photons(CBR)
anisotropies, 198
forêt Lyman-α, 67, 245
formation des structures top-down, 305
Friedmann
équation de, 32, 34, 35, 42
Y
L
PO
eﬀet de lentille gravitationnelle, 196
Index
sur la structure à grande échelle,
285
eﬀet Gunn-Peterson, 213
eﬀet Sachs–Wolfe, 308
eﬀet Sunyaev–Zel’dovich (SZ), 91, 93,
216, 315
eﬀondrement gravitationnel
dissipatif, 271
non-dissipatif, 271
eﬀondrement sphérique, 45, 46, 271
entrée dans le rayon de Hubble, 265,
277, 280, 292–294, 298, 301
amplitude de ﬂuctuation ∆H , 296
entropie, 220, 224, 226, 238, 254, 258
espace courbe et espace-temps courbe,
177
T
Y
L
PO
densité critique, 21
deutérium, 244, 245, 247, 263
diagramme couleur-magnitude, 58, 61,
62, 192
diagramme de Hubble, 18, 195
distance angulaire, 136, 193
distance de Hubble, 20
distance de luminosité, 135
distance propre, 175
distribution dans l’espace des phases,
39–41, 222, 227, 258, 322
ÉC
N
H
EC
E
U
IQ
H
C
TE
U
Q
I
N
géantes rouges du clump, 60, 63
géodésiques, 117–119, 132, 138–141
galaxies
E
Index
T
Y
L
PO
courbes de rotation, 50
gaz moléculaire comme matière noire,
87
gel, 220, 258, 259
électron–positron, 234, 235
et énergie libre, 220
et production d’entropie, 254, 255
neutrino, 239, 263
neutron, 243
nucléaire, 245
positron, 239, 261
wimps, 251
ÉC
E
L
O
hélium, 23, 55, 56, 97, 243–245, 249
halos galactiques, 14, 70, 71
high-z Supernova Search, 194, 195, 197
Hipparcos, 58, 61
horizon, 200, 216, 217
horizon classique, 207
horizon des événements, 208, 217
horizon des particules, 208
Hubble diagram, 194
Hubble Space Telescope, HST, 66, 90
ÉC
E
L
O
jauge synchrone, 294
métrique, 111, 117
métrique de Robertson-Walker , 128,
131
métrique de Schwarzschild, 141
machos, 83
magnitudes, 341
masse de Planck, 29, 333, 336
matière noire
dans les amas de galaxies, 76
dans les galaxies, 14, 16, 70, 71
matière noire baryonique, 83, 305
matière noire chaude, 304
matière noire froide (CDM), 23, 79, 247,
266
évolution des ﬂuctuations, 268, 269,
271
et amortissement de Silk, 269, 306
et anisotropies du CBR, 316
spectre des ﬂuctuations, 283, 284,
301, 303
Maxima, 96, 200, 313, 319
modèle standard de la physique des particules, 335
monopôles magnétiques, 51
E
L
O
N
H
EC
E
U
IQ
naines blanches, 64, 83, 191
naines brunes, 23
neutrinos, 24, 25, 64, 82, 94, 239, 304
comme matière noire, 24
densité, 37
et aeq , 38
masses, 27
mauvaise hélicité, 261
nombre d’espèces, 263
neutrons, 241, 243, 244, 263
nombre eﬀectif d’états de spin, 224, 225
Nuages de Magellan, 60, 62, 83, 84, 88,
90, 103
nucléosynthèse primordiale, 22, 94, 241
Y
L
PO
l’équation de Boltzmann , 227
lensing gravitationnel par, 145
lentille gravitationnelle, 76, 77, 141, 147
décalage temporel, 91, 145
397
faible, 146
microlensing, 83–85
loi de Hubble, 17, 20, 134, 135
longueur d’onde de Jeans, 288
T
Y
L
PO
inﬂation, 193, 205, 210, 211
durée de, 204, 207
et ΩT , 208, 209
et anisotropies du CBR, 319
et causalité, 204, 206
et ﬂuctuations primordiales, 298,
300
et homogénéité, 207
et ondes gravitationnelles, 320
et physique des particules, 212
et sortie de Hubble, 292
evolution des inhomogénéités, 295
interactions électro-faibles, 336
ÉC
N
H
EC
E
U
IQ
H
C
TE
U
Q
I
N
E
398
T
Y
L
PO
oscillations acoustiques, 287, 316
oscillations de neutrinos, 28
paradoxe d’Olbers, 217
paradoxe des jumeaux, 116
parallaxe, 58, 60
paramètre d’échelle a(t), 30, 35, 36, 43
paramètre d’échelle réduit â(t), 30
paramètre de biais, 282
paramètre de décélération q0 , 43, 134,
170, 199, 200
corrélation avec la distance, 133,
135, 193
et comptage, 215
et distance de luminosité, 136
et eﬀet SZ, 216
et photosphère en expansion, 216
et supernovae de type Ia, 96, 194
potentiel chimique, 223, 231, 252, 255,
258
pression, 165, 183, 223
négative, 165
principe anthropique, 52, 301
principe cosmologique, 21
problème de l’horizon, 200, 211
problème des Ω , 208, 211
ÉC
E
L
O
ÉC
E
L
O
réchauﬀement, 210
référentiels d’inertie , 114, 119
réionization, 213
rapport baryon/photon, η, 53, 94, 320
et baryogénèse, 262
et ﬂuctuations d’iso-courbure, 269
et la baryogénèse, 252
et la nucléosynthèse, 241, 244–247,
249, 259, 263
et vitesse du son, 317
rapport masse-luminosité, 14, 70, 71,
75, 76, 98
rayons X, 76, 92, 93, 98, 106–108, 286
recombinaison, 25, 48, 199, 259, 312,
314
E
L
O
Index
redshift, 19, 37, 38
redshift gravitationnel, 142
relation de Tully–Fisher, 28, 71, 74, 90,
164
relaxation violente, 271
reliquat de densité de particules, 238
reliquat de densité de particules , 220,
250
séquence principale, 56, 57, 60
sortie du rayon de Hubble, 292–294,
298
spectre de ﬂuctuations invariant d’échelle,
269, 296–298, 300, 313, 315,
316, 319
spectre de ﬂuctuations penché, 302, 303
spectre de puissance, 282
spectre des ﬂuctuation de densité, ∆k ,
266, 282, 284
évolution pour k −1 > dH , 294
dans les modèles de CDM, 301
spectre primordial, 296
statistique de Bose–Einstein, 222, 231
statistique de Fermi–Dirac, 222, 231
structures à grande échelle, 76
Supernova Cosmology Project, 66, 194,
195, 197
supernovae, 64, 71, 90, 96, 194
photosphère en expansion, 91, 216
supersymétrie, 24, 50, 79, 80, 250, 339
surface de dernière diﬀusion, 314
T
Y
L
PO
quasars (QSO), 67, 91, 213, 245, 248
quintessence, 29, 52
ÉC
N
H
EC
E
U
IQ
N
H
EC
E
U
IQ
taux de réaction, 219, 228
temps de Hubble, 20, 189, 193
temps propre, 111
tenseur énergie-impulsion, 162, 183
tenseur d’Einstein, 178
tenseur de Ricci, 183
tenseur de Riemann, 173, 183
théorème du viriel, 98, 277
théories de grande uniﬁcation (GUT),
47, 51, 208, 210, 253, 261
transformations de Lorentz, 116, 149,
153, 327
Y
L
PO
H
C
TE
U
Q
I
N
E
Index
T
Y
L
PO
transitions de phase, 29, 210, 225
trous noirs, 24, 67, 83
N
H
EC
E
U
IQ
399
unités naturelles, 20, 331
univers rebondissant, 191
univers stationnaire, 191
univers vide, 177
ÉC
E
L
O
violation de C et CP, 253
virialisation, 271, 274, 275, 277, 301
vitesse du son, 288, 290, 317, 324
vitesse particulière, 19, 278, 285, 287
wimps, 24, 247, 288
détection, 79
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
E
ÉC
E
L
O
ÉC
T
Y
L
PO
E
L
O
ÉC
N
H
EC
T
Y
L
PO
E
L
O
E
U
IQ
N
H
EC
Y
L
PO
E
U
IQ
H
C
TE
U
Q
I
N
Achevé d’imprimer en septembre 2004. Dépôt légal : 3e trimestre 2002
ISBN 2 - 7302 - 0925 - 5. Imprimé en France
E