serie2 limite continuite 4e math

L.S.C.J.Gafsa SERIE N°2 ( limites-continuité 4è.M) B.Tabbabi
Exercice 1 :
On considère la fonction f définie sur par
2
3
1
1 x sin si x < 0
x
f ( x )
1 x x si x 0
( C ) est la courbe de f dans un repère orthonormé
,,O i j
.
1.Calculer
lim ( )
xfx
et
()
lim
x
fx
x
.Interpréter graphiquement ces résultats.
2.On considère la fonction définie sur IR
*
par
sin
() x ux x
.
a.Vérifier que pour tout x<0 on a :
1
( ) 1 .f x xu x
.
b.Calculer
1
lim
xux
et en déduire
lim ( )
xfx
.
3.a.Vérifier que pour tout x < 0 on a :
22
1 x f ( x ) 1 x   
.
b.Calculer alors
x 0
lim f( x).
c.Etudier la continuité de f en 0.
d.Montrer que f est continue sur IR.
4.a.Montrer que l’équation f(x) = 0 admet dans
0,1
une solution unique .
b. Vérifier que
21
1.
5.Etudier chacune des limites suivantes :
x
x1
lim f x1
et
+
x1
x1
lim f x1
.
Exercice 2 :
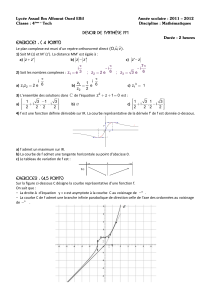
Dans la figure ci-contre,on a tracé les courbes
( ) ( )
fg
C et C
de deux fonctions f et g dans un
repère orthonormé
,,O i j
.
Chacune des deux courbes admet deux
asymptotes.
1.Par lecture graphique :
a.Donner
()
lim ( ) , lim
xx
fx
fx x
,
2
lim ( ) lim ( )
x
xg x et g x
.
b.Déterminer
2,g
et
,2f
.
c.Calculer
2
lim ( ) lim ( )
x
xf g x et f g x
.
2.On donne
50
2
g
a.Vérifier que f g est continue sur
2,
.
b.Montrer que l’équation f
3
() 2 gx

admet dans
5,3
2
une solution unique.
Exercice 3 :
On considère la fonction f définie sur par f ( x ) =
3
2
1 0
1 4 x > 0
x x si x
x x si
.
( C ) désigne la courbe de f dans le plan muni d'un repère orthonormé
,,O i j
.
1.Calculer
lim ( )
xfx
et
()
lim
x
fx
x
.Interpréter ces résultats graphiquement.
2.Montrer que ( C ) admet en + une asymptote oblique dont on donnera une équation.
3.Etudier la continuité de f en 0 puis sur .
4.a.Montrer que l'équation f ( x ) = 0 admet dans
1 ,0 
une solution unique .
b.Montrer que
2
1 1
.
c.Vérifier que pour tout réel x de
, 0 
on a : f ( x )
21
x x x
.
d.En déduire que la fonction g: x
3
1xx
x
est prolongeable par continuité en .
Exercice 4 :
Répondre par vrai ou faux en justifiant.
1.Si la fonction
f
est continue en un réel a alors f est continue en a.
2.f est une fonction continue sur IR.
a.Si l’équation
()f x x
admet une solution dans IR alors l’équation
()f f x x
admet une solution dans
IR.
b. Si l’équation
()f f x x
admet une solution dans IR alors l’équation
()f x x
admet une solution dans
IR 3.On donne ,ci-dessous le tableau de variation d’une fonction f définie et continue sur IR\
1
.
a.L’équation
( ) 0fx
admet dans IR\
1
exactement deux solutions.
b.
,1 0,f  
.
c.Pour tout réel x différent de 1,on a :
( ) .f x x
d.Pour tout x<1 on a :
( ) 1.f x x
e. La courbe de f admet exactement deux asymptotes.
* * * * * * *
x
0 1
f
0
1