Droites perpendiculaires et droites parallèles

Chapitre 6 ème
Droites perpendiculaires et droites parallèles
➢Tracer, par un point donné, la perpendiculaire ou la parallèle à une
droite donnée.
➢Médiatrice.
➢Hauteur d'un triangle.
➢Triangle rectangle.
➢Rectangle et carré.

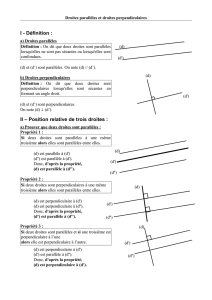
Définition :
Deux droites sécantes sont deux droites ayant un seul point commun.
Ce point est appelé le point d’intersection des droites.
(d’)
(d)
(d)//(d’)
A
B
D
C
Chapitre n° Droites perpendiculaires et droites parallèles
1) Définitions et notations
a) Droites sécantes :
Exemple :
Les droites (d) et (d’) sont sécantes au point A.
Le point A est le point d’intersection des droites (d) et (d’).
Remarque : (d’) se lit « d prime »
b) Droites perpendiculaires :
Exemple :
Les droites (AB) et (CD) sont perpendiculaires.
Notation :
On note (AB) (CD),le symbole «  » signifie « est perpendiculaire à ».
Remarques :
 Deux droites perpendiculaires sont sécantes.
 Il est inutile de coder les 4 angles droits sur le dessin. On en code un seul par un carré.
 On utilise une équerre pour tracer une droite perpendiculaire à une autre.
c) Droites parallèles:
Exemple :
Les droites (d) et (d’) n’ont aucun point commun : elles sont parallèles.
Notation :
On note (d)//(d’), le symbole « // » signifie « est parallèle à ».
Cas particulier :
Lorsque les points A,B et C sont alignés, les droites (AB) et (BC) ont une infinité de points communs.
Les droites (AB) et (BC) ne sont pas sécantes (elles n’ont pas un seul point commun mais une
infinité) et sont donc parallèles.
On dit aussi que les droites « (AB) et (BC) sont confondues ».
Définition :
Deux droites perpendiculaires sont deux droites qui se coupent en formant quatre angles droits.
Définition :
Deux droites parallèles sont deux droites qui ne sont pas sécantes.
B
A
C
(d)
(d’)
A

2) Construire la perpendiculaire à une droite passant par un point
Propriété :
Par un point donné M, on peut tracer une seule perpendiculaire (d') à une droite donnée (d).
Exemple : Tracer une droite (d) et place un point M n'appartenant pas à la droite (d).
Tracer la droite (d') perpendiculaire à la droite (d) passant par le point M.
On trace une droite (d)
et on place un point M.
On place l'un des côtés de
l'angle droit de l'équerre sur
la droite (d) et l'autre côté
sur M.
On prolonge la droite à la
règle.
On nomme la droite (d')
et on code l'angle droit
par un carré.
Cas particulier :
La médiatrice d'un segment est la droite qui coupe ce segment perpendiculairement en son milieu.
Exemple : Tracer un segment [OS] de longueur 5 cm puis sa médiatrice.
On trace un segment [OS].
(dessins suivants agrandis)
On place son milieu et
on le code.
On trace la droite
perpendiculaire au segment qui
passe par ce milieu.
On code l'angle droit
par un carré.
3) Construire la parallèle à une droite passant par un point
Propriété :
Par un point donné M, on peut tracer une seule parallèle (d') à une droite donnée (d).
Exemple : Tracer une droite (d) et place un point M n'appartenant pas à la droite (d).
Tracer la droite (d') parallèle à la droite (d) passant par le point M.
On trace une droite
(d) et on place un
point M.
On place l'un des côtés de
l'angle droit de l'équerre
sur la droite (d).
On fait coulisser l'équerre le
long de la règle, jusqu'au
point M, sans bouger la règle.
On trace ainsi la
droite (d').
Propriétés: (admises)
 Si deux droites sont perpendiculaires à une même droite, alors elles sont parallèles.
 Si deux droites sont parallèles, alors toute perpendiculaire à l’une est perpendiculaire à l’autre.
M(d)
(d')
M
(d)
O
S
¤
¤
¤
¤
S
O
M
(d)
M
(d) M(d)
M
(d)
(d')
M
(d)
S
¤
O
¤
M
(d)
OS

4) T riangle rectangle
Définition :
Un triangle rectangle est un triangle qui a un angle droit.
Le côté opposé à l'angle droit est appelé « hypoténuse ».
Exemple : Construire un triangle KHI rectangle en K tel que KI = 5 cm et HI = 7 cm.
On trace un segment [KI]
de longueur 5 cm.
(dessins suivants agrandis)
On trace la droite
perpendiculaire en K à (KI)
et on code l'angle droit.
On trace un arc de cercle
de centre I et de rayon
7 cm coupant la
perpendiculaire en H.
On trace le
segment [HI].
5) Rectangle
Définition : Un rectangle est un quadrilatère dont les 4 angles sont droits.
Exemple : Construire un rectangle CHOU tel que CH = 9 cm et HO = 12 cm.
   On trace un segment [HC] ;
 On trace la perpendiculaire à ce segment en H ;
 On place un point O sur cette perpendiculaire
tel que OH = 12 cm ;
 On trace la perpendiculaire à (OH) en O ;
 On trace la perpendiculaire à (HC) en C ;
 Ces deux droites se coupent en U.
Cas particulier : Un carré est un rectangle dont les 4 côtés sont de même longueur.
KIKII
K
H
HC
HC
OOU
HC
OU
HC H C
HC
O
H
C
O
KI
I
K
H
[HI] est l'hypoténuse
HC

6) Hauteur
Définition :
Une « hauteur » d'un triangle est une droite qui passe par un sommet du triangle
et qui est perpendiculaire à la droite portant le côté opposé à ce sommet.
Exemple :
AB=3 cm, BC=8 cm et AC=6 cm.
Remarques:
➢Pour tracer la hauteur (CH) il fallait prolonger le côté [AB] (trait en pointillé), pour obtenir le
point H qui est le pied de la hauteur.
➢Il reste à tracer la hauteur issue du sommet B... au travail.
C
A
B
(AG) hauteur issue du sommet A
G est le «pied» de la hauteur
issue du sommet A
[CB] côté «opposé» au sommet A
G
(AG)  (CB)
C
A
B
(CH) hauteur issue
du sommet C
H est le «pied» de la hauteur
issue du sommet C
H
[AB] côté «opposé» au sommet C
(CH)  (AB)