Géométrie II

smo
osm
Olympiades Suisses de Mathématiques
Géométrie II
Daniel Sprecher
Actualisé: 30 janvier 2016
vers. 2.0.0
Table des matières
1 Triangles semblables 2
2 Working Backward 4
3 La puissance d’un point 5
4 La ligne de puissance 6
5 La droite de Simson 8
6 Céva et Ménélaüs 9
6.1 Céva...................................... 10
6.2 Ménélaüs ................................... 11
7 Points spéciaux du triangle 13
7.1 Lecentredegravité.............................. 13
7.2 Le centre du cercle inscrit . . . . . . . . . . . . . . . . . . . . . . . . . . 14
7.3 Les centres des cercles exinscrits . . . . . . . . . . . . . . . . . . . . . . . 14
7.4 Le centre du cercle circonscrit et l’orthocentre . . . . . . . . . . . . . . . 15
8 Quadrilatères circonscrits 15

Introduction
Cette deuxième partie a pour but de vous présenter les techniques les plus importantes
qui interviennent dans la résolution d’exercices de géométrie aux Olympiades de Mathé-
matiques. On vous recommande particulièrement de lire les démonstrations étape par
étape et d’essayer de vous souvenir des idées principales, cela vous permettra de mieux
comprendre les rapports entre les différents aspects de la géométrie. Toutefois le plus
important reste le contenu des théorèmes.
En comparaison avec la première partie, ce script contient moins de figures et moins
d’exemples. Cela a pour but de vous forcer à faire vos propres esquisses et à résoudre les
exercices par vous-mêmes, ce qui constitue un bon entraînement.
1 Triangles semblables
Les théorèmes de Thalès ont sûrement été traités à l’école. Nous ne les répéterons donc
ici que brièvement, sans preuve et sans exercices. Pour l’application de ces théorèmes on
vous propose les deux premiers exercices de ce chapitre.
Théorème 1.1 (Premier théorème de Thalès).Soient aet bdeux droites parallèles et
Sun point n’étant situé sur aucune des deux droites. Un rayon quelconque partant de S
coupe aen Aet ben B. Un deuxième rayon coupe aen A0et ben B0. On a
SA
SA0=SB SB0⇔SA SB =SA0 SB0⇔SA AB =SA0 A0B0.
Théorème 1.2 (Deuxième théorème de Thalès).Dans le même arrangement que ci-
dessus, on a de plus
AA0
BB0=SA SB .
Il faut savoir que la réciproque du premier théorème est également valable. Pour la
formuler correctement, nous devons utiliser des distances orientées. Par conséquent il
peut y avoir des rapports négatifs. Soient X, Y et Ztrois points distincts, étant situés
sur une droite dans cet ordre . Dans ce cas le rapport XY
Y Z est positif, car les vecteurs
−−→
XY et −→ Y Z ont la même direction. En revanche XZ
ZY est négatif, puisque les vecteurs
correspondants pointent dans des directions opposées. Désormais quand nous aurons
affaire à des rapports ou des produits orientés, nous noterons cela entre parenthèses.
2

Théorème 1.3 (Réciproque du premier théorème de Thalès).Soient S, A, B sur une
droite donnée et S, A0, B0sur une autre avec
SA
SB =SA0 SB0(distances orientées)
alors les droites AA0et BB0sont parallèles.
La réciproque du deuxième théorème de Thalès n’est pas valable. On le voit en construi-
sant le cercle autour de Aavec le rayon AA0. En général, ce cercle coupe SB0encore une
fois en P6=A0. Dans cet arrangement on a
AP
BB0=SA SB
mais les droites AP et BB0ne sont pas parallèles.
Le passage des théorèmes de Thalès à la similitude se fait en décalant 4SAA0et 4SBB0
arbitrairement dans le plan (Sse divise ainsi en S1et S2). Les longueurs des côtés ne
changent pas et les relations déjà établies restent valables. Une condition suffisante pour
la similitude est que les deux triangles aient les mêmes angles. On écrit alors
4S1AA0∼ 4S2BB0.
Avec la réciproque du théorème de la similitude il faut être attentif. Pour décider
quelle réciproque est vraie et quelle ne l’est pas, on considère la réciproque du théorème de
Thalès. Ici des distances ordonnées n’ont pas de sens. Montrer d’abord que deux triangles
possèdent un angle égal et puis considérer le rapport des côtés avoisinant cet angle est
une bonne variante. Voici un exemple de cette stratégie.
Exemple 1. Soit un carré ABCD et soit Mle milieu du côté AB. La perpendiculaire
MC passant par Mcoupe AD en K. Montrer que les triangles 4CMB et 4CKM sont
semblables.
Solution. Pour démontrer la similitude de deux triangles on peut soit passer directement
par la chasse aux angles (en montrant que tous les trois angles sont égaux), soit appliquer
la réciproque du théorème de la similitude, ce qu’on fera ici.
Par hypothèse on a ∠MBC =∠KMC = 90◦. Il nous reste à montrer
MK
MC =BM BC .
Après une brève chasse aux angles on trouve que 4MBC et 4KAM sont semblables.
Cela implique que MK
MC =MA BC =BM BC .
La deuxième équation repose sur le fait que Mest le milieu de AB.
Une dernière remarque : pour montrer que deux n-gones avec n > 3sont semblables, il ne
suffit pas de montrer que tous les angles sont égaux. Comme illustration on considère un
trapèze qu’on allonge le long de ses côtés parallèles. Les angles restent inchangés tandis
que les rapports des côtés changent.
3

2 Working Backward
Le Working Backward est une stratégie importante pour trouver des résultats qu’on
n’arrive pas à prouver par la chasse aux angles. Puisque quelques preuves dans ce script
(le théorème sur les quadrilatères circonscrits, théorème 6, Géométrie I, en est déjà un
exemple) utilisent cette méthode on l’introduit ici et on va en présenter deux exemples
typiques. L’approche du Working Backward ressemble à ce qui suit :
Supposons qu’on doit montrer qu’un point Pa une certaine propriété. On construit
d’abord un point P0, duquel on sait qu’il possède ladite propriété. Puis on démontre qu’il
n’y a qu’un seul point avec cette propriété et qu’ainsi les points Pet P0coïncident.
Exemple 2. Soit 4ABC un triangle et Sle point d’intersection de la bissectrice de
∠BAC avec la médiatrice de BC. Alors Sappartient au cercle circonscrit au triangle
4ABC.
Solution. Si on essaye de résoudre l’exercice tel qu’il est donné, on remarque vite que
l’on n’arrive pas à avancer. Le truc ici consiste à définir le point S0comme le point
d’intersection de la bissectrice de ∠BAC avec le cercle circonscrit au triangle 4ABC.
L’avantage de cela est que désormais nous pouvons utiliser tout ce que nous savons à
propos des angles dans le cercle.
Avec le théorème de l’angle inscrit et en utilisant la bissectrice, nous obtenons :
∠S0BC =∠S0AC =∠BAS0=∠BCS0.
Le triangle 4BS0Cest ainsi isocèle, ce qui nous donne donc que S0appartient à la
médiatrice de BC. Alors S0appartient en même temps à la bissectrice de ∠BAC et à
la médiatrice de BC, ce qui signifie évidemment que S=S0. Comme S0appartient par
définition au cercle circonscrit au triangle 4ABC, nous avons terminé.
Exemple 3. Soient 4ABC et 4AB0C0deux triangles semblables ayant le même sens et
Acomme sommet commun. Montrer que A,B,Cet le point d’intersection des droites
BB0et CC0se trouvent sur un même cercle.
Solution. Appelons Ple point d’intersection de BB0et CC0et, comme toujours, α, β
et γles angles des triangles. On veut montrer que Pse trouve sur le cercle circonscrit
de 4ABC. Avec une chasse aux angles directe on n’y arrive pas. Par contre on a une
symétrie entre les points B, C et B0, C0ce qui implique que P, s’il se trouve sur le cercle
circonscrit de 4ABC, doit également se trouver sur le cercle circonscrit de 4AB0C0.
C’est une raison suffisante pour définir un point P0comme point d’intersection des deux
cercles. On a fini si on arrive à démontrer que B, P 0, B0et C, P 0, C0sont colinéaires. Donc
P0est également le point d’intersection de BB0et CC0et il ne peut en avoir qu’un, ce
qui entraîne P=P0.
4

Pour démontrer la colinéarité de B, P 0et B0on a recours à la chasse aux angles :
∠BP 0B0=∠BP 0A+∠AP 0C0+∠C0P0B0
=∠BCA +∠AB0C0+∠C0AB0
=γ+β+α
= 180◦.
Par la symétrie entre B, B0et C, C0, les points C, P 0, C0sont aussi colinéaires.
Deux remarques pour finir. Ce qu’on peut observer à travers ces exemples est valable assez
généralement. Quand on a affaire à des angles, c’est plus pratique d’avoir des points sur
des cercles que d’avoir des points définis par des droites. Avec le Working Backward on
peut redéfinir des points afin de pouvoir appliquer toute la machinerie des angles dans le
cercle.
La deuxième remarque se réfère aux arguments de symétrie qu’on a invoqués dans le
deuxième exemple. Si vous écrivez dans votre solution "...par symétrie on a...", n’oubliez
jamais de préciser entre quels points on a une symétrie. D’ailleurs, "il y a symétrie entre
B, B0et C, C0" signifie que, si on échange Bavec Cet B0avec C0, on a toujours un
arrangement qui satisfait les conditions de l’énoncé.
3 La puissance d’un point
Euclide a déjà mentionné et prouvé ce théorème important dans son oeuvre Les élé-
ments.
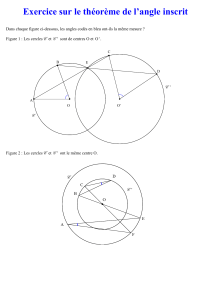
Théorème 3.1 (Théorème de la puissance).Soit un point Pdonné et un cercle k.
Appelons Aet Bles deux points d’intersection de kavec une droite gquelconque passant
par P. On appelle puissance de Ppar rapport à kle produit P A ·P B. Ce produit est
indépendant du choix de g.
Preuve. Considérons la figure 1. Soit AB et A0B0deux droites arbitraires passant par
Pqui se trouve en dehors du cercle. Les triangles 4P AA0et 4P B0Bsont semblables,
puisque ∠B0BA = 180◦−∠B0A0A=∠P A0A. Il s’ensuit que
P A
P A0=P B0 P B
CQFD. Le cas avec Pà l’intérieur du cercle se démontre de façon analogue. Les points
sur le cercle ont tous une puissance de 0.
Très souvent on applique le théorème de la puissance avec la tangente au cercle passant
par P. Soit Tle point où la tangente touche le cercle. On a alors P A ·P B =P T 2.
5