Fiche 20 – La démonstration

Fiche 20 – La démonstration
En mathématique la démonstration permet de prouver qu’un résultat est vrai.
A/ Les règles de base
La logique mathématique repose sur plusieurs « principes » fondamentaux :
1) Un énoncé mathématique est soit vrai, soit faux.
2) Des exemples ou des constatations faites sur une figure ne prouvent pas qu’un énoncé est vrai.
3) Un exemple qui ne vérifie pas un énoncé mathématique suffit pour prouver que cet énoncé est faux (voir
premier principe) : c’est un contre-exemple.
B/ Définition et structure d’une propriété
On appelle propriété un énoncé mathématique vrai.
Un propriété est composée : d’une hypothèse ;
d‘une conclusion.
Dans les propriétés de la forme « Si …, alors … »,
l’hypothèse est placée après le « Si » et la conclusion après le « alors ».
C/ Structure d’une démonstration
Une démonstration fonctionne toujours sur le même principe : en partant de données dont on est sûr et en
utilisant une propriété reprenant ces données dans son hypothèse, on arrive à avoir une nouvelle donnée.
Une démonstration va être construite à l’aide de chaînon(s) déductif(s) :
Hypothèse : c’est ce que l’on connaît.
Propriété : on l’énonce sauf si elle porte un nom (Thalès…).
Conclusion : c’est ce que l’on veut prouver.
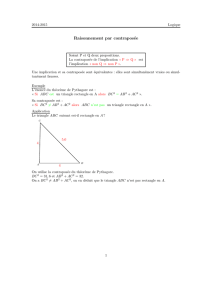
Exemple : Soit ABC un triangle tel que AC = 2 cm et BC = 2 cm.
Démontrer que ABC est isocèle.
Hypothèse : [AC] et [BC] ont la même mesure
Propriété : Si un triangle a deux côtés de même mesure,
alors il est isocèle
Conclusion : ABC est isocèle (en C).
D/ Réciproque et contraposée d’une propriété de la forme « Si …, alors … »
La réciproque de la propriété utilisée dans l’exemple
du C/ est :
« Si un triangle est isocèle, alors il a deux côtés de
même mesure ».
Cet énoncé étant vrai ; donc cette réciproque est
aussi une propriété.
Certaines réciproques de propriétés sont des énoncés
faux (donc ne sont pas elles-même des propriétés).
Exemple : « Si un entier se termine par 2, alors il est
pair » est une propriété (énoncé toujours vrai).
Sa réciproque est : « Si un entier est pair, alors il se
termine par 2 » qui est un énoncé faux puisque 4 est
un entier qui est pair mais qui ne se termine pas par 2
(contre-exemple prouvant que l’énoncé est faux).
La contraposée de la propriété utilisée dans l’exemple
du C/ est :
« Si un triangle n’est pas isocèle, alors il n’a pas deux
côtés de même mesure ».
La contraposée d’une propriété est toujours vraie !
C’est donc forcément elle-même une propriété.
L’hypothèse étant ce de quoi on part (ce que l’on sait) et la
conclusion ce à quoi on arrive (ce que l’on prouve).
On pourra utiliser toutes les propriétés vues dans le cours
depuis la 6
ème
.
On construit la contraposée d’une propriété en prenant
la négation et en échangeant son hypothèse et sa
conclusion. (« nier » une phrase, c’est dire son contraire)
Si un énoncé n’est pas vrai que dans 1 seul cas, on dit qu’il est faux
On peut construire un chaînon en « partant de la fin ». En
effet on connaît toujours la conclusion du chaînon (c’est ce
que l’on veut prouver), ensuite il suffit de trouver la
propriété ayant une conclusion correspondante et une
hypothèse faisant parti de ce que l’on sait.
L’hypothèse du chaînon doit correspondre
à celle de la propriété.
La conclusion de la propriété doit
correspondre à celle du chaînon.
La très grande majorité des propriétés
utilisées dans des démonstrations est
de cette forme.
Pour nier, on met très souvent « ne … pas »
autour du verbe !
On a donc le droit d’utiliser la contraposée d’une
propriété vue en cours même si cette contraposée n’y a
pas été formellement écrite.
Par contre, on ne peut utiliser que les réciproques
écrites dans le cours (puisque certaines sont fausses !)
On construit la réciproque d’une propriété en
échangeant son hypothèse et sa conclusion.