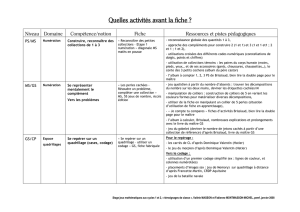
Dossier : Le calcul à l`école primaire

Accueil > Le mensuel > La recherche
Dossier : Le calcul à l'école primaire
Robien impose ses idées sur le calcul
"Je souhaite que, dès le cours préparatoire, les maîtres consacrent 15 à 20 minutes,
tous les jours, à des exercices de calcul mental pour construire patiemment ces
automatismes qui manquent aujourd'hui à beaucoup trop d'élèves".
Lors d'une conférence de presse,le 23 janvier, le ministre de l’éducation nationale a annoncé une circulaire
sur l'enseignement des mathématiques à l'école primaire, début mars.
L'avis de la Commission de l'académie des sciences recommande l'introduction des 4 opérations très tôt : "
L'enseignement du calcul doit commencer par une pratique simultanée de la numération et des quatre
opérations, une gradation en complexité se faisant entre maternelle et fin de primaire, jusqu’aux nombres
décimaux et aux fractions".
S'inspirant des travaux de S. Dehaene, membre de la commission, la commission estime que " à l’exception d’une petite fraction
d ’enfants souffrant de dyscalculie d’origine génétique ou périnatale, tous les enfants possèdent très précocement une intuition
arithmétique" et fait allusion à une mémoire de travail qui serait libérée par l'exercice du calcul mental : "l’automatisation du calcul
s’accompagne d’une diminution massive de l’activation du cortex préfrontal, correspondant à une libération des ressources mentales
pour d’autres tâches". Elle recommande le retour aux "nombres concrets" des programmes anciens.
Le ministre revient donc aux programmes de 1945 et va même au-delà puisque il introduit les 4 opérations avant le CP. Une prise
de position qui rappelle ses affirmations sur la lecture ou, plus récemment, sur la grammaire. Celles-ci avaient été largement
contestées par les spécialistes et les cadres du système éducatif au point, pour la lecture, d'aboutir à un texte rappelant les
programmes antérieurs.
Selon l'AFP, le discours ministériel est vivement critiqué par les syndicats enseignants. "Ce qui nous étonne toujours, c'est que le
ministre détient la vérité, ce qu'il dit mérite un débat contradictoire" estime Philippe Niemec, du SE-Unsa. "Travailler les quatre
opérations le même jour, c'est impossible, illusoire et dangereux, c'est un peu comme si on apprenait dans la même séquence de
l'anglais, de l'allemand et de l'espagnol" affirme Gilles Moindrot, secrétaire général du Snuipp.
Le discours ministériel et l'avis de l'académie des sciences
http://www.education.gouv.fr/cid4420/academie-des-sciences-place- du -calcul-dans-l-enseignement-primaire.html
http://fr.news.yahoo.com/23012007/202/calcul-mental-apprentissages-precoces-robien-dessine-sa-reforme-des-maths.html
Le dossier spécial du Café
http://www.cafepedagogique.net/lesdossiers/Pages/maths06_index.aspx
Des divisions pour un calcul politique
L'annonce par Gilles de Robien du retour aux 4 opérations (addition, soustraction, multiplication et division) dès le cours
préparatoire et même dès la grande section de maternelle rencontrera probablement l'approbation de nombreux parents, angoissés
devant les progrès scolaires de leurs enfants. Pourtant, pour de nombreux experts, cette décision est préjudiciable aux acquisitions
mathématiques et elle ne se justifie par aucune découverte scientifique assurée. Il faut donc chercher ailleurs ses motivations.
La commission Robien n'est pas forcément compétente.
Composée de brillants mathématiciens, la commission réunie par l'académie des sciences à la demande de Robien, réunit des
mathématiciens de renom. Pour autant ceux-ci n'ont pas de compétence pédagogique et ne sont pas des spécialistes de
l'enseignement des mathématiques. Ils en sont d'ailleurs conscients puisque eux-mêmes recommandent de ne pas appliquer tel
quelles leurs recommandations mais de les soumettre à débat.
Les experts sont hostiles à l'apprentissage précoce de la division.
C'est ce qui ressort des contributions apportées au Café pédagogique ces derniers mois par plusieurs spécialistes de l'apprentissage
des mathématiques. Ainsi pour Rémi Brissiaud, maître de conférences à l'IUFM de Versailles, "une écriture comme 21 : 3 renvoie
principalement à deux sortes de situations, celles où l'on partage 21 unités en 3 parts égales, évidemment, mais aussi celles où, par
exemple, l'on cherche combien d'objets à 3 euros il est possible d'acheter avec 21 euros (en 21, combien de fois 3 ?). Or, les deux
sortes de situation n'ont rien de commun a priori.. D'ailleurs, les recherches disponibles montrent que les élèves ne mettraient pas
ces deux sortes de situation en relation s'ils ne fréquentaient pas l'école. Certains chercheurs parlent de " division-partage " dans le
premier cas et de " division-mesure " ou " division-groupement " dans le second (en a, combien de fois b ?)… Les mêmes
chercheurs, en général, considèrent qu'il convient d'éviter un usage précoce du mot " division " et de ses symboles opératoires (les
deux points et la potence) pour ne pas laisser croire aux élèves que diviser = partager. En effet, ceux qui ont le plus de difficultés
s'enferment dans cette conception de la division et cela les conduit à échouer dans la résolution des autres problèmes de division.
Ce n'est pas avant le CE2 que la quasi-totalité des enfants est capable d'accéder à une compréhension de la division comme
opération permettant de traiter à la fois le partage et la mesure-groupement. Si, pour enseigner les 4 opérations dès le CP, il fallait
revenir à des pratiques pédagogiques qui associent le formalisme de la division à la seule situation de partage, ce serait

probablement à l'origine d'une aggravation de l'échec en résolution de problèmes". Un avis qui est corroboré par Joël Briand,
Maître de conférences en mathématiques, qui rappelle aussi que "la division est en acte, très tôt, dans les apprentissages
mathématiques. Il n'y a donc pas de temps perdu".
Robien s'appuie sur une théorie de l'inné contestée.
A l'appui des recommandations de la commission, les travaux de Stanislas Dehaene, lui-même membre de cette commission.
Mathématicien et neuropsychologue, il a mis en évidence que les humains ont une capacité naturelle à se former une
représentation approximative des quantités. Cette découverte est importante. Mais ses conséquences sur l'apprentissage des
mathématiques font débat. Certains estiment que cette représentation innée ne joue aucun rôle dans la conceptualisation des
nombres. Or c'est cette idée de l'inné qui pousse la commission à démarrer précocement les 4 opérations.
Revenir aux anciens programmes est dangereux.
" Si nous devions revenir aux programmes de 1945,… ces programmes devaient créer à nouveau… un ennui important dans les
classes du fait de la répétition, un désintérêt généralisé des enseignants pour le fonctionnement intellectuel de leurs élèves, un
enseignement élitiste parce que seuls les enfants qui s’auto-questionnent progressent en résolution de problèmes". En mai 2006,
Rémi Brissiaud rappelait que les anciens programmes avaient été remplacés pour des raisons sérieuses. A l'ennui s'ajoute les
difficultés à maîtriser les opérations.
Robien va au- delà des recommandations de la commission .
Mais le plus surprenant c'est que Robien ne tient pas compte de la prudence de la commission. " La complexité de la question
posée, et sa déclinaison en programmes et instructions pour les inspecteurs (IEN) et maîtres, impose une grande prudence dans
l’affirmation de recommandations et conclusions" déclare la commission. "Il ne serait en effet que trop aisé, dans de telles
situations, de solliciter les experts au-delà de ce qu’ils sont en mesure d’affirmer ou de provoquer des incompréhensions profondes
chez les maîtres. C’est pourquoi l’Académie, en formulant cet Avis, considérerait comme prudent de s’abstenir de préconisations
impératives immédiates, et recommande que les observations ici présentées puissent être corroborées d’analyses plus
approfondies, le cas échéant contradictoires". Ces règles de prudence d'une commission pas sûre d'elle-même sont balayées par
Robien qui annonce une circulaire dans quelques jours. Autrement dit, la commission elle –même est instrumentalisée.
Qu'est ce qui anime le ministre ?
Théorie invérifiée, choix contestable, décision prématurée, ce n'est à vrai dire pas la première circulaire Robien qui cumule ces
reproches. La grande force de ce texte c'est de s'appuyer sur deux revendications fortes des parents.
D'abord l'angoisse des parents devant le risque d'échec scolaire. Elle est perceptible dès l'école maternelle où nombre de parents
exigent que les apprentissages scolaires commencent au plus tôt. Elle est déjà captée par certains éditeurs qui vendent des cahiers
de vacances de maternelle, permettant des "révisions". La bataille pour l'accès aux "bonnes" maternelles, celles où l'on prépare le
primaire dès la petite section, est bien engagée également.
La seconde revendication est celle de la personnalisation. En effet les rythmes d'apprentissage des enfants sont différents, même si
à l'arrivée l'écart d'acquisition n'est pas forcément important. Les parents fonctionnent un peu par sécurité : dans le cas où mon
enfant serait capable d'apprendre tôt les 4 opérations, il faut essayer et généraliser. Ils ne voient pas les éventuelles retombées
négatives personnelles et s'intéressent peu au rôle social de l'école.
Appuyée sur ces attentes parentales, la circulaire Robien apparaît une nouvelle fois comme un objet politique. On peut craindre
qu'elle aggrave la méfiance entre le monde enseignant et les parents.
Le dossier spécial du Café
http://www.cafepedagogique.net/lesdossiers/Pages/maths06_index.aspx
La future réforme soumise aux experts
Rémi Brissiaud, maître de conférence de psychologie cognitive, a bien voulu réagir à l'avis de la Commission
de l'académie des sciences. Il apporte une lecture décapante. Relevant " la grande naïveté dont font preuve
les auteurs quand ils abordent certains thèmes pédagogiques", il montre que leur approche des 4 opérations
s'inspire des programmes de 1970.
" Serait-il raisonnable de préconiser aujourd’hui un retour aux pratiques anciennes en oubliant totalement les
raisons qui avaient conduit à leur évolution, soutenue alors par de grands mathématiciens comme André
Lichnerowitz, inquiets des échecs de trop nombreux élèves ?" demande R. Brissiaud. " Il n’y a rien de plus
décourageant pour les enseignants que cette absence de progression dans les idées pédagogiques avancées
par des responsables de l’éducation nationale qui ne se donnent pas la peine de connaître les débats
pédagogiques anciens. Rien n’est plus décourageant que l’impression de voir la pédagogie à l’école subir un
incessant et obscur mouvement de balancier".
Mais R. Brissiaud va plus loin en contestant la qualité des membres de la commission et leur choix théorique. " Le ministre, lorsqu’il
a annoncé la date du 23 janvier pour la publication du rapport, en a présenté les auteurs comme des « spécialistes français » du
calcul à l’école et les auteurs eux-mêmes, dans leur Avis, se qualifient d’ « experts » . Certes, ils ont en commun d’être d’éminents
spécialistes de la recherche en mathématiques ou de l’usage de mathématiques de haut niveau à des fins de recherches en
physique, en astrophysique, en traitement du signal, etc. Mais en quoi cela leur confère- t -il une compétence de « spécialistes de
l’enseignement du calcul à l’école maternelle et élémentaire » ? " demande R. Brissiaud.
Puisque l'avis s'appuie sur les travaux de S. Dehaene, cognitiviste membre de la commission, R. Brissiaud rappelle que sa théorie
est critiquée. D'ailleurs la commission appelle elle-même à prendre en copte son avis avec une grande prudence. "L’Académie, en
formulant cet Avis, considérerait comme prudent de s’abstenir de préconisations impératives immédiates, et recommande que les
observations ici présentées puissent être corroborées d’analyses plus approfondies, le cas échéant contradictoires" Dans ces
conditions, pour R. Brissiaud, " toute décision de modifier les programmes en se référant à l’Avis des académiciens sans prendre en
compte leur appel à la prudence serait solliciter leur texte bien au-delà de ce qu’ils disent, ce serait instrumentaliser leur propos".

Joël Briand, maître de conférences de mathématiques, a bien voulu nous donner son avis au vue du texte publié par Le Monde. "Le
récent rapport de l’Inspection Générale de mathématiques… note que les résultats des élèves sont assez constants sur une période
de plus d’un demi-siècle à l’entrée du collège alors que celui-ci accueille maintenant tous les élèves. Il y a donc à poursuivre un
travail de mise en ligne des programmes de 2002, en particulier de préciser ce qui y est appelé « situations problèmes » … Il est
donc utile de ne pas se focaliser sur les recherches cognitives mais aussi d’interroger les recherches en didactique des
mathématiques… Le milieu des enseignants de l’école primaire a besoin de sérénité, a besoin d’aide pour l’application des
programmes actuels qui sont de qualité".
Le dossier spécial du Café
http://www.cafepedagogique.net/lesdossiers/Pages/maths06_index.aspx
Les billevesées de l'Académie pour G. Vergnaud
"Je trouve bien légère la reprise, dans l'avis de l'Académie, des billevesées concernant les compétences prétendument numériques
des bébés. Ce sont des billevesées parce que la perception par les bébés d'une différence entre deux quantités, voire d'une
inégalité, ne peut pas être considérée comme une conceptualisation du nombre. La reconnaissance de la propriété d'addition est
une condition nécessaire. Les travaux sont nombreux qui donnent un âge plus proche de quatre ou cinq ans (dans le meilleur des
cas et sous certaines conditions) pour les premières compétences proprement numériques des enfants". Gérard Vergnaud, ancien
directeur du Groupement de recherche "Didactique et acquisition des connaissances scientifiques", ne mâche pas ses mots.
Sur le site de J. Nimier, il publie une analyse critique de l'avis remis par la Commission de l'académie des sciences sur
l'enseignement du calcul à l'école primaire. Après bien d'autres scientifiques, sa critique est sévère. "Un peu de réflexion
épistémologique sur la conceptualisation mathématique ne serait pas de trop dans la réflexion du Ministre et de ses conseillers.
Qu'on me comprenne bien ! Je trouve positif que les Académiciens aient répondu au Ministre. En outre plusieurs des points qu'ils
retiennent sont de bon sens, et assortis d'une recommandation de prudence. Je trouve par contre étrange que le Ministre
s'intéresse si peu à la didactique des mathématiques et à la psychologie des apprentissages mathématiques… Faire appel à de
grands savants pour obtenir d'eux un avis n'est pas une démarche déraisonnable, même s'ils n'ont pas toutes les compétences
qu'on leur prête. Ils peuvent eux aussi être victimes de naïvetés, plus dangereuses qu'on ne le pense sans examen… Il est du devoir
du Ministre de se tenir informé et de renoncer au mépris dans lequel il tient les didactiques, les sciences de l'éducation, les IUFM, et
même le savoir d'expérience acquis par les enseignants au cours de leur pratique… Le sens commun est bel et bon, mais
radicalement insuffisant pour penser les phénomènes complexes. Les connaissances scientifiques se construisent aussi contre le
sens commun, et pas seulement en s'appuyant sur lui".
http://perso.orange.fr/jacques.nimier/calcul_vergnaud.htm
Les mathématiciens jugent sévèrement la réforme Robien sur le calcul
La récente prise de position de Robien en faveur de la réforme du calcul à l'école primaire a déjà été analysée sur le site du Café
pédagogique par plusieurs didacticiens des mathématiques qui en ont souligné le caractère rétrograde et dangereux pour les
apprentissages.
L'équipe Educmaths de l'Institut national de recherche pédagogique a eu l'idée de consulter trois mathématiciens de renom sur le
texte émis parla commission de l'Académie des sciences.
Ainsi Guy Brousseau, professeur honoraire des Universités, Médaille Félix Klein 2003 de l'ICMI (International Commission on
Mathematic Instruction), président d'honneur de l'ARDM (Association pour la Recherche en Didactique des Mathématiques) analyse
point par point le texte de la commission. Il s'attarde plus longuement sur le 4ème point, celui qui prévoit le retour des 4 opérations
dès la maternelle.
"Il est le plus discutable. Il peut recevoir des interprétations très diverses. Certaines sont très acceptables et décrivent ce que font la
majorité des enseignants aujourd'hui, d'autres complètement extrêmes sont tout à fait dangereuses. Le public prendra ce texte au
pied de la lettre et s'attendra à voir les enfants poser et « calculer » mentalement des divisions, dès l'école maternelle. Ce qui ne
peut qu'accroître les malentendus avec les professeurs qui connaissent leur métier. Et conduire les autres à effectuer des dressages
dont nous connaissons bien les méfaits… La lecture de ce texte ne me convainc pas que les mesures qu'il préconise soient une
réponse adéquate aux difficultés rencontrées aujourd'hui dans l'enseignement des mathématiques, ni même que leur action aura
les effets qui sont espérés".
"La déclaration fondatrice sur laquelle s'ouvre l'avis donne un exemple des raisonnements et des évidences sur lesquels il s'appuie
parfois. Elle est formée d'une prémisse explicite composée de deux déclarations : « à l'issue du collège et du Lycée, chez filles et
garçons, de nombreuses observations convergentes indiquent une insuffisante maîtrise du calcul » et « les fondements du calcul se
mettent indiscutablement en place à l'école primaire » . La conclusion qui en est tirée est implicite, ce qui la fait tenir d'autant plus
pour évidente : c'est la mise en place du calcul à l'école primaire qu'il faut réformer. Peut-être serait-ce utile, mais sûrement pas à
cause de cette inférence curieuse. En fait les connaissances à la sortie des études dépendent moins de leur toute première initiation
que de l'usage qui en est fait tout au long des études, et de celui qui en sera fait après. Les influences s'exercent aussi bien en
amont qu'en aval. Il faut regarder l'usage réel qui est fait du calcul humain, mental ou « à la plume » , dans notre société, de ce
qu'en voient les enfants, de l'opinion qu'en ont les professeurs des différents niveaux, de l'attention qu'ils peuvent y porter etc…
L'idée que l'on pourrait enfermer définitivement un apprentissage de bases dans un socle sur lequel on pourrait ensuite développer
des activités intelligentes sans jamais revenir sur ces prérequis est un fantasme récurrent de la didactique spontanée… Associé à
l'usage incontrôlé d'une évaluation, il est un des obstacles majeurs, toujours renaissant aux progrès que proposent la didactique et
l'épistémologie".
Guy Brousseau conclue :"Il y a plus de vingt cinq siècles les mathématiques comme nous les entendons sont nées de la rupture avec
la très ancienne tradition de l'ésotérisme qui permettait à des experts de conseiller les tyrans sans avoir d'autres comptes à rendre
que leurs résultats. La démocratie, naissante elle aussi, avait heureusement d'autres exigences. Nous pourrions nous en inspirer
aujourd'hui en matière de connaissances sur l'enseignement des mathématiques".
Jean-Pierre Kahane, académicien des sciences, ancien président de la Commission de Réflexion sur l'Enseignement des
Mathématiques et membre de la commission qui a émis cet avis contesté à G. de Robien n'est pas fier du résultat. "La galère étant
lancée, il y avait à ramer, en évitant les pires écueils, et en préservant les chances d'une vraie discussion au sein de l'Académie et

avec tous ceux qui ont réfléchi à ces questions avant elle. Le climat dans la galère était tendu… Sur les questions d'enseignement
comme de recherche, il serait imprudent de s'en remettre sans examen à ce que dit l'Académie. Mais il serait dommage de ne
retirer de ce quelle dit que ce qui conforte le pouvoir en place". On ne saurait être plus clair.
http://educmath.inrp.fr/Educmath/en-debat/place- du -calcul-enseignement-primaire
Rémi Brissiaud invite les chercheurs à réagir
"Concernant la lecture, les chercheurs en psychologie cognitive, en sciences de l'éducation, en linguistique et en neuroscience ont
su se réunir pour dire au ministre que le retour au b-a, ba n'est pas la solution aux difficultés d'enseignement de l'écrit et, depuis,
celui-ci a cessé de faire du retour à la méthode syllabique un argument de campagne. Il serait vraisemblablement déterminant
aujourd'hui que les chercheurs en didactique des mathématiques se rassemblent et sollicitent leurs collègues des autres disciplines
pour prendre une initiative similaire". L'annonce par Gilles de Robien d'une réforme de l'enseignement du calcul au primaire,
ramenant celui-ci sur les programmes de 1945, a suscité des réactions de spécialistes sur les sites du Café pédagogique et de
l'Inrp.
Rémi Brissiaud,maître de conférence en psychologie cognitive, invite les chercheurs à se mobiliser pour communiquer leurs craintes
à l'opinion publique. "Si l'on veut mettre en garde le public contre le simplisme des slogans du ministre, il me semble qu'il faut se
concentrer sur un petit nombre d'idées fortes. Il faut rappeler, par exemple, que le partage n'est pas la division, que le faire croire
aux élèves est potentiellement source d'échec et que l'enseignement formel de la division au cycle 2 est ainsi une menace pour la
réussite scolaire. Il faut dire que rendre obligatoire cet enseignement sans expérimentation préalable sérieuse tient de
l'irresponsabilité".
Le dossier spécial du Café
http://www.cafepedagogique.net/lesdossiers/Pages/maths06_index.aspx