PROPORTIONNALITE DES LONGUEURS DANS UN TRIANGLE I

PROPORTIONNALITE DES LONGUEURS DANS UN TRIANGLE
I Deux parallèles coupant deux sécantes
Propriété
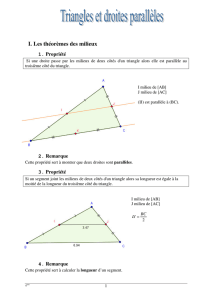
Dans un triangle ABC où M est un point du côté [AB] et N est un point du côté [AC], si les droites (MN) et
(BC) sont parallèles
alors AM
AB = AN AC = MN BC
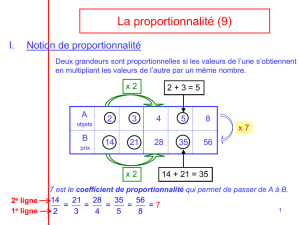
Les longueurs des côtés du triangle ABC sont proportionnelles aux longueurs des côtés correspondant du
triangle AMN. Le tableau suivant est un tableau de proportionnalité.
Triangle ABC
AB
AC
BC
Triangle AMN
AM
AN
MN
II Agrandissement – réduction
Définition
Une figure f ’ est un agrandissement d’une figure f lorsque toutes les longueurs de la figure f ’sont obtenues
en multipliant les longueurs de la figure f par un même nombre k strictement supérieur à 1. Ce nombre k est
appelé coefficient d’agrandissement.
Agrandissement de coefficient : ………
Une figure f ’ est une réduction d’une figure f lorsque toutes les longueurs de la figure f ’sont obtenues en
multipliant les longueurs de la figure f par un même nombre k strictement inférieur à 1. Ce nombre k est
appelé coefficient de réduction.
Propriété
Dans un agrandissement (ou une réduction) de rapport k, les angles sont conservés, la perpendicularité, le
parallélisme sont conservés.
Propriété
Dans un agrandissement ou une réduction de rapport k :
a) Le périmètre de la figure transformée est multiplié par k. p’ = k × p.
b) L’aire de la figure transformée est multipliée par k². a’ = k² × a
c) Le volume de la figure transformée est multiplié par k3. v ’ = k3 × v