Nom : Pr´ enom : Groupe :

Nom :
Pr´enom :
Groupe :
Interrogation de Graphes
–
Dur´ee : 30 minutes
(r´epondre sur la feuille)
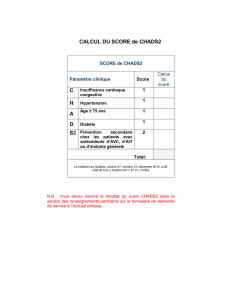
Exercice 1.
A. Ce graphe est-il connexe ?
B. Est-il eul´erien (et pourquoi) ?
C. Quel est le plus grand degr´e ?
D. Ce graphe est-il r´egulier (et pourquoi) ?
E. Quelle est la longueur du plus petit cycle ´el´ementaire ?
(´el´ementaire = pas deux fois le mˆeme arc)
F. Est-il planaire ? Si oui montrez-le par un dessin.
(planaire = il est possible de dessiner ce graphe avec des arˆetes
droites ou courb´ees, sans qu’aucune ne se croise)
Exercice 2 (Parcours de graphes).Expliquez la diff´erence entre un parcours en largeur (BFS) et un
parcours en profondeur (DFS).
Exercice 3 (Dijkstra).A l’aide du pseudo-code ci-dessous, ex´ecutez `a la main l’algorithme de Dijkstra
sur le graphe donn´e, en prenant pour sommet initial A. L’union des plus courts chemins ainsi calcul´es
forme un arbre, qui devra ˆetre bien visible sur le dessin. Vous laisserez ´egalement, et volontairement, des
traces de votre ex´ecution sur le dessin, afin de me convaincre que vous avez bien ex´ecut´e l’algorithme.
vsrc .score ←0
for all v∈V\ {vsrc}do
v.score ←+∞
finished ← ∅ // Sommets qu’on a fini de traiter
while finished 6=Vdo
vtmp ←min{V\finished}// Choisi le sommet non-fini de
plus petit score
for all v∈neighbors(vtmp)do
if v /∈finished then
if vtmp.score +weight((v, vtmp )) < v.score then
v.score ←vtmp .score +weight((v, vtmp))
v.parent ←vtmp
finished ←finished ∪ {vtmp}
A
B
CD
E
F
7
9
14
10 15
11
2
6
9
1