méthode rectangles et trapèzes

TD
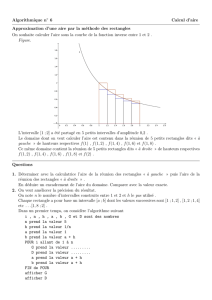
Calcul intégral : méthode des rectangles et des trapèzes
TS
On considère la fonction définie , sur  par 
 .  est continue et positive sur .
On ne sait pas , en Terminale S , calculer une primitive de  .
On souhaite calculer une valeur approchée de l’intégrale 
 pour   
I. Méthode des rectangles
On divise l’intervalle [0 ; ] en  intervalles de même amplitude 
1. On appelle « aire inférieure » l’aire des rectangles situés sous la courbe :
a. Déterminer en fonction de  et de  la largeur et la longueur des rectangles « inférieurs »
b. Expliquer pourquoi l’aire inférieure est égale à : 
2. On appelle « aire supérieure » l’aire des rectangles situés au-dessus de la courbe :
3. De même , exprimer à l’aide d’une somme l’aire supérieure notée  .
4. On donne l’algorithme suivant :
Variables : 
Entrée : Saisir 
Saisir 
Traitement :   
Pour  allant de  à 
 ……………………
FinPour
Sortie : Afficher 
Afficher 
a. Compléter l’algorithme suivant pour que:
 Dans la variable G soit calculée l’aire
inférieure
 Dans la variable D soit calculée l’aire
supérieure
b. Programmer cet algorithme à l’aide de
votre calculatrice et le tester pour

Aide à la programmation
Pour utiliser une fonction  dans un programme
Casio graph 35
TI 82
Dans le menu GRAPH : écrire la fonction en Y1
Dans le menu PGRM :
Taper Y1(A) si l’on veut calculer l’image de A par la
fonction
Pour trouver la lettre Y1 :
Touche VARS puis choisir GRPH , Yn et taper 1
Dans le menu  : écrire la fonction en Y1
Dans le menu PGRM :
Taper Y1(A) si l’on veut calculer l’image de A par la
fonction
Pour trouver la lettre Y1 :
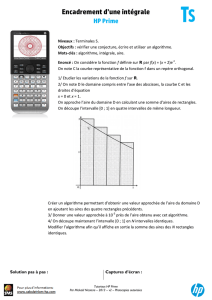
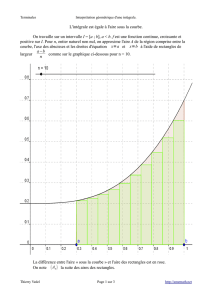
II. Méthode des trapèzes avec le logiciel Geogebra
1. Principe
Ci-contre la représentation graphique de la fonction
, notée 
On partage l’intervalle [0 ;1] en deux intervalles
d’amplitude 0,5 et on construit :
 Les points A , I et B de la courbe 
d’abscisses 0 ; 0,5 et 1
 Les trapèzes OAIH et HIBK
En utilisant les trapèzes OAIH et HIBK , déterminer
une valeur approchée de 
2. Pour augmenter la précision de cette valeur approchée , on partage l’intervalle [0 ;1] en  intervalles de la
forme [
 pour  variant de   
a. Construire à l’aide du logiciel Geogebra la courbe représentative de  : 
b. Créer un curseu r  variant de 1 à 100
c. Entrer dans le champ de saisie : SommeTrapèzes[f,0,1,n]
d. Combien faut-il de trapèzes pour que l’aire de cette somme soit environ égale à 3,14 à 0,01 près ?
e. En utilisant la fonctionnalité SommeInférieure[…] de Geogebra , déterminer le nombre de « rectangles
inférieurs » qu’il faut utiliser pour obtenir la même valeur approchée.
3. Expliquer pourquoi la somme des aires des trapèzes de largeur 
 est égale à 
4. En utilisant le logiciel Geogebra , déterminer une valeur approchée de cette somme  pour   
5. Compléter l’algorithme précédent pour qu’il affiche une valeur approchée de 
 par la méthode des
trapèzes et le programmer sur votre calculatrice .