07 fonctions lineaires et affines eleve

Page 1 sur 8

- FONCTIONS LINEAIRES ET AFFINES-

NOM :

Prénom :

Classe :

Fonctions linéaires et affines

Chapitre :

Date :

A/ Définition d’une fonction linéaire

1) Activité

Pour transporter des petits colis, l'agence Vavite propose un prix proportionnel

à la distance : 0,40 € par km.

Calculer le prix payé pour de petits colis pour 50 km, puis pour 200 km.

50 km => 0,40 50 = 20 => 20 €

200 km => 0,40 200 = 80 => 80 €

Le prix est fonction de la distance. On désigne par x la distance en kilomètres.

On appelle f la fonction qui, au nombre x de kilomètres, fait correspondre le prix payé f(x)

Exprimer le prix payé, en euros, en fonction de la distance, pour de petits colis.

f(x) = 0,40 x

Calculer f(80). Puis, déterminer x tel que f(x) = 80

f(80) = 0,40 80 = 32

f(200) = 80 (vu à la première question)

2) A retenir

.........................................................................................................................................................................

Exemple 1 :

On donne les six fonctions suivantes définies pour tout nombre x :

f(x) = – x ; g(x) = 1,2x ; h(x) = x ; i(x) = 3x² ; j(x) = 2x + 3 ; k(x) = x (avec x 0)

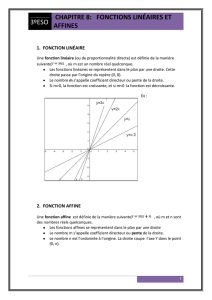
Les fonctions f, g, h sont linéaires.

Les fonctions i, j, k ne sont pas linéaires.

Exemple 2 :

Le périmètre P d’un carrée de coté x est égal 4x, il est proportionnel à la longueur de sont coté x.

On définit une fonction linaire p de coefficient 4 telle que p(x) = 4x

Page 2 sur 8

- FONCTIONS LINEAIRES ET AFFINES-

B/ Représentation d’une fonction linéaire

1) Activité

Soit f est la fonction de l’activité précédente.

x est la distance en km et f(x) est le prix à payer en euros.

Compléter le tableau ci-dessous :

x

10

50

100

200

f(x)

4

20

40

80

Dans un repère orthogonal, placer les points de coordonnées :

(10 ; f(10)) ; (50 ; f(50)) ; (100 ; f(100)) ; (200 ; f(200))

Vérifier que ces points sont alignés avec l’origine du repère.

Tracer la droite D qui les joint.

2) A retenir

.........................................................................................................................................................................

0

20

40

60

80

100

120

140

160

180

200

220

x

0

10

20

30

40

50

60

70

80

90

100

f(x)

Page 3 sur 8

- FONCTIONS LINEAIRES ET AFFINES-

Exemple :

On donne deux fonctions linéaires f et g définies par :

f(x) = 2x

g(x) = – 0,5x

La représentation graphique de f est la droite D d'équation y = 2x

Celle de g est la droite D' d'équation y = – 0,5x

C/ Définition d’une fonction affine

1) Activité

Pour transporter de gros colis, l'agence Vavite propose le tarif suivant :

0,40 € par km, plus un fixe de 30 €.

Calculer le prix pour 50 km, puis pour 200 km pour de gros colis.

50 km => 0,40 50 + 30 = 50 => 50 €

200 km => 0,40 200 + 30 = 110 => 110 €

Le prix est fonction de la distance. On désigne par x la distance en kilomètres.

On appelle g la fonction qui, au nombre x de kilomètres, fait correspondre le prix payé g(x)

Exprimer le prix payé, en euros, en fonction de la distance, pour de gros colis.

f(x) = 0,40x + 30

Calculer g(110). Puis, déterminer x tel que g(x) = 110

f(110) = 0,40 110 + 30 = 74

f(200) = 110 (vu à la première question)

2) A retenir

.........................................................................................................................................................................

Exemple :

On donne les six fonctions suivantes définies pour tout nombre x :

f(x) = 2x – 4 ; g(x) = – 4x ; h(x) = x + ; i(x) = x² + 1 ; j(x) = (2x + 3)² ; k(x) = 8x + x (avec x 0)

Les fonctions f, g, h sont affines, de plus la fonction g est linéaire (b = 0).

Les fonctions i, j, k ne sont pas linéaires.

-3

-2

-1

0

1

2

3

-3

-2

-1

0

1

2

3

y x

Page 4 sur 8

- FONCTIONS LINEAIRES ET AFFINES-

D/ Représentation d’une fonction affine

1) Activité

Soit g est la fonction de l’activité précédente.

x est la distance en km et g(x) est le prix à payer en euros.

Compléter le tableau ci-dessous :

x

10

50

100

200

g(x)

34

50

70

110

Dans un repère orthogonal, placer les points de coordonnées :

(10 ; g(10)) ; (50 ; g(50)) ; (100 ; g(100)) ; (200 ; g(200))

Vérifier que ces points sont alignés.

Tracer la droite D’ qui les joint.

2) A retenir

.........................................................................................................................................................................

0

20

40

60

80

100

120

140

160

180

200

220

x

0

10

20

30

40

50

60

70

80

90

100

110

120

g(x)

Page 5 sur 8

- FONCTIONS LINEAIRES ET AFFINES-

Exemple :

On donne deux fonctions linéaires f et g définies par :

f(x) = x – 2

g(x) = – x + 3

La représentation graphique de f est la droite D d'équation y = x – 2

Celle de g est la droite D' d'équation y = – x + 3

E/ Sens de variation d’une fonction affine

1) Activité

Soit f et g deux fonctions affines définies respectivement par :

f(x) = 2x – 3

g(x) = – 3x + 1

Compléter le tableau ci-dessous :

Les valeurs de sont rangés par ordre croissant.

x

– 2

– 1

0

1

2

f(x)

– 7

– 5

– 3

– 1

1

g(x)

7

4

1

– 2

– 5

Dans quel ordre sont rangées les valeurs de f(x) ? et pour g(x) ?

Les valeurs de f(x) sont rangées dans l’ordre croissant.

Les valeurs de g(x) sont rangées dans l’ordre décroissant.

Quelle est la différence entre les fonctions f et g ?

f a un coefficient directeur positif alors que g a un coefficient directeur négatif.

2) A retenir

.........................................................................................................................................................................

-3

-2

-1

0

1

2

3

-3

-2

-1

0

1