div de tension et courant et théorème de théveninl

La page de l'aide mémoire (ON5HQ)
DIVISEURS DE TENSION ET DE COURANT
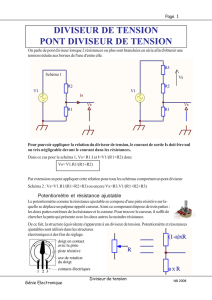
DIVISEUR DE TENSION : La tension U appliquée sur un diviseur de tension constitué de deux
résistances en série se divise dans un rapport proportionnel aux valeurs des résistances.
U1 = U • R1 / (R1 + R2)
U2 = U • R2 / (R1 + R2)
Remarque
Dans le cas où le diviseur de tension est chargé par une résistance RCH dont la valeur n'est pas très élevée par
rapport à celle de R1, il fut, dans les formules, remplacer R1 par :
(R1 • RCH) / (R1 + RCH)
Ex :
(R1 • RCH) / (R1 + RCH)
U1 = U • -----------------------------------(R1 • RCH) / (R1 + RCH) + R2
Applications numériques
1 : Le diviseur de tension est composé de R1 = 4,7 kΩ et R2 = 33 kΩ. La tension U appliquée est de 100 V.
Quelle est la valeur de U1 ?
U1 = (100 x 4,7) / (4,7 + 33) = 12,46V
2 : Dans l'exemple précédent, que devient U1 lorsque le diviseur est chargé par 10 kΩ ?
R1 est remplacé par :
(4,7 x 10) / (4,7 + 10) ~ 3,2 kΩ
La nouvelle valeur de U1est:
100 x 3,2 / (3,2 + 33) = 8.84 V
DIVISEUR DE COURANT : Le courant I envoyé sur un diviseur de courant constitué de deux
résistances en parallèle se divise dans un rapport inversement proportionnel aux valeurs des résistances.
I1 = I • R2 / (R1 + R2)
I2 = I • R1 / (R1 + R2)
Applications numériques
1 . Un courant de 4 A est appliqué à un diviseur de courant dont les résistances sont R1 = 50 Ω et I2 = 150 Ω.
Quelles sont les valeur de I1 et I2 ?
I1 = 4 x 150 / (50 + 150) = 3 A
I2 = 4 x 50 / (50 + 150) = 1 A
2 . Dans le circuit ci-dessous, alimenté par un courant IT de 1,5 A, nous voulons alimenter une lampe L de 12 Ω
devant être traversée par 0,5 A. Quelle doit être la valeur de R2 ?
Cette résistance R2 doit dériver un courant I2 égal à IT – I1, soit I2 = 1 A.
Pour le calcul de R2, nous transformons la formule :
I2 = IT • R1 / (R1 +R2)
Ce qui donne :
R2 = R1 • ((IT / I2) – 1)
Valeur de R2 :
12 x ((1,5/1) – 1) = 6 Ω
THEOREME DE THEVENIN
Ce théorème permet de simplifier les circuits actifs électriques.
THEOREME DE THEVENIN : Un réseau complexe comprenant une ou plusieurs sources peut être
remplacé par un circuit équivalent comprenant une source à tension constante et une résistance en série.
La source de tension constante donne une tension égale à la tension en circuit ouvert du réseau complexe.
La résistance en série à une valeur égale à celle vue de la sortie de circuit complexe lorsque la ou les sources
internes sont en court-circuit.
Méthode de calcul.
a) Aucun circuit n'étant connecté entre A et B, la tension entre ces bornes est :
U = E • R2 / (R1 + R2)
b) La source étant en court-circuit, le résistance vue entre A et B est :
RS = (R1 • R2) / (R1 + R2)
Application numérique :
1° Dans le schéma ci-dessus (méthode de calcul), on à : E = 80 V et R1 = R2 = 20 Ω. Quel est l'équivalent de
Thévenin ?
La tension entre A et B est :
80 x 20 / (20 + 20) = 40 V
La résistance vue entre A et B (la source E étant court-circuitée) est de :
(20 x 20) / (20 + 20) = 10 Ω
Le circuit est équivalent à une source te tension U = 40 V en série avec une résistance série RS = 10 Ω