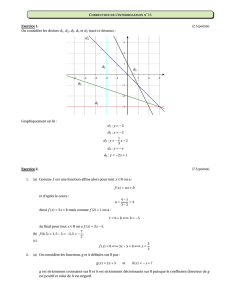
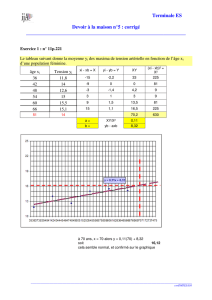
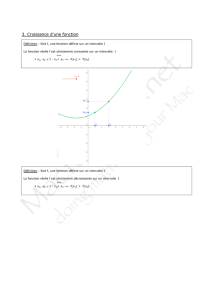
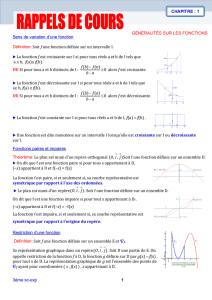
fichecours

Cours de Mathématiques
1re S2
Première partie
Logique
1
Chapitre 1
Logique élémentaire
Définition 1.1 (Qu’est ce qu’une assertion ?). On définit une assertion
comme toute phrase syntaxiquement correcte à laquelle on peut assigner
une valeur de vérité : Vrai, ou Faux
Soit H et C deux assertions quelconques, vraies ou fausses. "V" siginifie
Vrai et "F" signifie Faux. On utilise des tableaux de vérité pour définir les
symboles logiques.
– Notion de disjonction, de conjonction et de négation : "ou" est le symbole de disjonction, "et" est le symbole de conjonction, "non" est le
symbole de négation.
Tableau de vérité
H C H ou C H et C non H
V V
V
V
F
V F
V
F
F
F V
V
F
V
F F
F
F
V
– Notion d’implication : H et C sont deux assertions, "=⇒" est le symbole d’implication
Tableau de vérité
H C H =⇒ C
V V
V
V F
F
F V
V
F F
V
H =⇒ C : H est une condition suffisante à C
C =⇒ H : H est une condition nécessaire à C
2
CHAPITRE 1. LOGIQUE ÉLÉMENTAIRE
3
– Notion d’équivalence : H et C sont deux assertions, "⇐⇒" est le symbole d’équivalence
Tableau de vérité
H C H ⇐⇒ C
V V
V
V F
F
F V
F
F F
V
Deuxième partie
Algèbre
4
Chapitre 2
Outils d’algèbre et d’analyse
I
Calcul numérique et algébrique
1
Vocabulaire et notation
– Comment décrire un ensemble ?
i). On donne la liste exhaustive des éléments de l’ensemble. Cette
écriture s’appelle l’écriture en extension.
ex : L’ensemle des élèves de première S2 est {Adjerad; . . . ; Zerbib}
ii). On donne la nature des éléments de l’ensemble et leur propriété
caractéristique 1 C’est l’écriture en compréhension.
ex : [2 ; 5] = {r ; r ∈ R / 2 6 r 6 5}
Vocabulaire
–
–
–
–
Algèbre : transformation d’expressions contenant des variables
développer : transformer une expression pour obtenir une somme
factoriser : transformer une expression pour obtenir un produit
réduire : conserver la nature de l’expression, mais en conservant le moins
de termes possible
– simplifier : transformer l’expression de manière à répondre à un type
de problème posé
– Une identité est une égalité qui dépend d’une ou plusieurs variables et
qui est vraie pour toutes les valeurs de la ou les variables.
– Une équation est une égalité qui dépend d’une ou plusieurs inconnues
et qui n’est pas vraie pour toutes les valeurs de la ou les inconnues.
1. Propriété que seuls les éléments de l’ensemble ont. À différencier avec une propriété
remarquable : propriété qu’ont les éléments de l’ensemble.
5
CHAPITRE 2. OUTILS D’ALGÈBRE ET D’ANALYSE
2
6
Théorèmes, propositions et résultats
Théorème 2.2 (distributivité de la multiplicaton par rapport à l’addition).
Pour tous a, b, c ∈ R, a (b + c) = ab + ac
Théorème 2.3.
Pour tous a, b, c ∈ R, a = b ⇐⇒ a + c = b + c
Pour tous a, b ∈ R, pour tout c ∈ R∗ , a = b ⇐⇒ ac = bc
Proposition 2.4. Le carré d’une somme de termes est égale à la somme de
la somme des carrés de ces termes et à la somme des doubles produits de ces
termes.
Proposition 2.5. Soit n, k ∈ N, avec k 6 n. On note Ckn l’entier naturel de
la k eme colonne et de la neme ligne du triangle de pascal (à noter : les numéros
des lignes et des colonnes commencent à partir de 0). On a :
Ckn + Ck+1
= Ck+1
n
n+1
(2.1)
Ckn = Cn−k
n
(2.2)
L’égalité 2.2 se comprend comme le fait que les lignes du triangle de Pascal
sont « symétriques ».
De plus avec la convention de notation 00 = 1, on a pour tous réels a et b et
pour tout entier naturel n :
(a + b)n = C0n an + . . . + Ckn an−k bk + . . . + Cnn bn
On a pour tous réels a et b et pour tout entier naturel non nul n :
an − bn = (a − b)(an−1 + . . . + an−1−k bk + . . . + bn−1 )
3
Expressions polynomiales du premier et du deuxième
degré (à une variable réelle)
Définition 2.6. On appelle expression polynomiale du premier degré à une
variable réelle x toute expression du type ax + b où a et b sont des constantes
réelles avec a 6= 0.
On nomme a le coefficient dominant et b le coefficient constant
CHAPITRE 2. OUTILS D’ALGÈBRE ET D’ANALYSE
7
Définition 2.7. Un zéro d’une expression dépendant d’une variable est une
valeur de la variable pour laquelle l’expression est nulle.
On peut aussi utiliser le terme racine.
Théorème 2.8. Pour tout a ∈ R∗ , pour tout b ∈ R :
b
Pour tout x ∈ R, ax + b = 0 ⇐⇒ x = −
a
b
Pour tout x ∈ −∞; − , ax + b est du signe contraire de a au sens strict.
a
b
Pour tout x ∈ − ; +∞ , ax + b est du signe de a au sens strict.
a
Définition 2.9. On appelle expression polynomiale du deuxième degré à une
variable réelle x toute expression de la forme ax2 + bx + c où a, b, c sont des
constantes réelles avec a 6= 0.
On appelle a le coefficient dominant et c le coefficient constant.
Soit x un réel. On a, avec les notations précédentes :
b
c
2
2
ax + bx + c = a x + x +
a
a
#
"
2 2
b
b
b
c
= a x2 + x +
−
+
a
2a
2a
a
"
#
2
b
b2 − 4ac
=a x+
−
2a
4a2
La dernière expression s’appelle la forme canonique.
On appelle discriminant de l’expression polynomiale du deuxième degré
2
ax + bx + c de la variable réelle x, le réel b2 − 4ac.
Premier Cas : Supposons que le discriminant est strictement négatif, alors :
b2 − 4ac
>0
−
4a2
2
b2 − 4ac
b
>0
Donc pour tout x ∈ R, x +
−
2a
4a2
"
#
2
b
b2 − 4ac
Ainsi a x +
−
est du signe de a au sens strict.
2a
4a2
alors ax2 + bx + c est du signe de a au sens strict.
CHAPITRE 2. OUTILS D’ALGÈBRE ET D’ANALYSE
8
Cette expression n’a pas de zéro. Supposons qu’elle soit factorisable en
produit de deux expressions polynomiales du premier degré distinctes
ou confondues. De ce fait elle aurait alors au moins un zéro. Donc elle
n’est pas factorisable en produit de deux expressions polynomiales du
premier degré.
Second Cas : Supposons que le discriminant est positif ou nul, alors :
#
"
2
2
b
−
4ac
b
−
ax2 + bx + c = a x +
2a
4a2
√
√
b
b2 − 4ac
b2 − 4ac
b
=a x+
−
x+
+
2a
2a
2a
2a
!
√
√
−b − b2 + 4ac
−b + b2 − 4ac
x−
=a x−
2a
2a
−b +
√
b2 − 4ac
2a
Cette expression a deux zéros distincts ou confondus :
√
−b − b2 + 4ac
et
. Les zéros sont confondus lorsque le discriminant est
2a
nul et les zéros sont distincts lorsque le discriminant est strictement
positif.
b
La somme des zéros est égale à : − .
a
c
Le produit des zéros est égal à : .
a
b
- Si b2 − 4ac = 0, les deux zéros sont confondus et valent − .
2a
- Si b2 − 4ac > 0, les deux zéros sont distincts :
Quand a > 0 :
√
√
−b − b2 − 4ac
−b + b2 − 4ac
<
2a
2a
Quand a < 0 :
−b +
√
√
b2 − 4ac
−b − b2 − 4ac
<
2a
2a
On note α le plus petit des zéros et β l’autre zéro.
- b2 − 4ac = 0 ⇐⇒ α = β. De plus si on a bien b2 − 4ac = 0, alors pour
b
tout réel x distinct de − , ax2 + bx + c est du signe de a au sens
2a
strict.
CHAPITRE 2. OUTILS D’ALGÈBRE ET D’ANALYSE
9
- b2 − 4ac > 0 ⇐⇒ α < β et si on a bien b2 − 4ac > 0, alors pour tout
x ∈ ]−∞ ; α[ ∪ ]β ; +∞[, ax2 + bx + c est du signe de a au sens strict,
et pour tout x ∈ ]α ; β[, ax2 + bx + c est du signe contraire de a au
sens strict.
4
Racines, puissances et valeur absolue
Définition 2.10. La racine carrée d’un réel positif ou nul a est le réel positif
ou nul b, tel que b2 = a
Définition 2.11. La valeur absolue d’un réel a, notée |a|, est le réel a si
a > 0 et le réel −a si a < 0.
Définition 2.12. Soit a un réel et b un entier naturel, avec b > 2. On note
ab le produit de b facteurs égaux à a. On a :
ab = |a × .{z
. . × a}
b fois
a est appelé l’argument et b l’exposant.
Théorème 2.13. Pour tout réel a, pour tous b et c des entiers naturels
supérieurs ou égaux à 2, on a : ab+c = ab ac .
À partir de cette règle de calcul, on s’aperçoit que : 3 × 34 = 35 , par
exemple. De ce fait on est amené à penser qu’on pourrait dire que 3 = 31 , bien
que l’on n’ait pas définit cette notation. De la même manière, on remarque
que 53+0 = 53 = 53 × 1, ainsi on peut penser que 50 = 1. On est alors tenté
d’ajouter à la définition 2.12 que pour tout réel a, a1 = a et que a0 = 1.
Cependant on savait que jusqu’ici que la propriété « pour tout entier naturel
b supérieur ou égal à 2, on a 0b = 0 » était vraie, en généralisant, on devrait
avoir 00 = 0, or on vient de dire que 00 = 1. On a donc une incompatibilité
entre ces deux propriétés. On décide alors de ne pas définir 00 (sauf convention
de notation). On obtient alors la définition suivante :
Définition 2.14. Soit a un réel non nul et b un entier naturel. Si b > 2, on
reprend la définition 2.12. Si b = 1, on a ab = a et si b = 0, alors on a ab = 1.
Définition 2.15. Soit a un réel non nul et b un entier relatif strictement
négatif. On définit ab tel que :
1
a = −b =
a
b
−b
1
a
CHAPITRE 2. OUTILS D’ALGÈBRE ET D’ANALYSE
10
Proposition 2.16. Soit a, b, c et d des réels tels que les différentes écritures
suivantes sont définies. On a :
ab+c = ab ac
c
ab = abc
II
Équations
1
Concepts
2
Stratégies de résolution
3
Systèmes
(a × b)c = ac × bc
c
c
a(b ) = ab
CHAPITRE 2. OUTILS D’ALGÈBRE ET D’ANALYSE
III
1
11
Fonctions et applications
Concepts
Définition 2.17 (fonction). On appelle fonction tout triplet (E, F, Γ) où :
– E est un ensemble, on l’appelle ensemble de départ.
– F est un ensemble, on l’appelle ensemble d’arrivée
– Γ est un « phénomène » qui permet d’associer à chaque élément de E,
soit rien, soit un unique élément de F
Notations et vocabulaires
Soit E et F des ensembles. On peut noter « f une fonction de E vers
F » : « f : E −→ F ». De même on peut noter « f une fonction de E
vers F qui à tout élément x de son ensemble de définition associe un élément
y de F »
f : E −→ F
x 7−→ y
Soit x ∈ E et y ∈ F tels que par f à x on associe y. On appelle y l’image
de x par f et x un antécédent de y par f . L’image de x par f , quand elle
existe, est notée f (x), on notera souvent f : x 7→ f (x) . On ne peut pas
donner de symbole pour l’antécédent faute d’unicité, en effet il peut ne pas
y avoir unicité.
Définition 2.18. (ensemble de définition) On appelle ensemble de défintion
d’une fonction, l’ensemble des éléments de son ensemble d’arrivée qui ont une
image par cette fonction. Lorsque l’on considérera une fonction f , on notera
souvent Df l’ensemble de définition de f .
Définition 2.19 (application). On appelle application toute fonction, telle
que tous les éléments de son ensemble d’arrivée ont une image par cette
fonction. Une application est donc une fonction dont l’ensemble de départ et
l’ensemble de définition sont confondus.
2
Composition de fonctions
Définition 2.20. Soit E, F et G des ensembles, et soit f et g des fonctions
respectivement de E vers F , et de F vers G. On construit une nouvelle
fonction h de E vers G et qui à tout x de E associe l’image par g de l’image
par f de x (si elle existe). On note cette fonction g ◦ f et on a :
g ◦ f : E −→ G
x 7−→ g(f (x))
CHAPITRE 2. OUTILS D’ALGÈBRE ET D’ANALYSE
12
Question 2.21. La composée de deux applications (compatibles pour la composition) est-elle une application ?
Proposition 2.22. Soit E, F et G des ensembles, et soit f et g des fonctions
respectivement de E vers F , et de F vers G. Notons Df , Dg et Dg◦f les
ensembles de définition respectifs de f , g et g ◦ f . On a :
Dg◦f = {x ; x ∈ E/ x ∈ Df et f (x) ∈ Dg }
IV
Les fonctions en analyse
Définition 2.23 (fonction numérique). On appelle fonction numérique toute
fonction dont l’ensemble d’arrivée est un ensemble de nombres
On considérera ici des fonctions numériques d’une variable réelle, et plus
précisément des fonctions de R vers R, notamment pour pouvoir les composer.
1
Opérations sur les fonctions
Soit f et g des fonctions de R vers R, et soit α un réel.
– addition des fonctions :
f + g : R −→ R
x 7−→ f (x) + g(x)
– multiplication des fonctions :
f g : R −→ R
x 7−→ f (x)g(x)
– multiplication d’une fonction par un réel :
αf : R −→ R
x 7−→ αf (x)
– passage à l’inverse :
1
: R −→ R
f
x 7−→
1
f (x)
CHAPITRE 2. OUTILS D’ALGÈBRE ET D’ANALYSE
13
– division de fonctions :
f
g
: R −→ R
x 7−→
f (x)
g(x)
– composition des fonctions :
g ◦ f : R −→ R
x 7−→ g(f (x))
Fonctions de référence
Soit f une fonction de R vers R.
– fonctions affines :
f est une fonction affine s’il existe deux réels a et b tels que pour tout
réel x, f (x) = ax + b
– fonctions polynomiales de degré 2 :
f est une fonction polynomiale de degré 2 s’il existe 3 réels a, b et c,
avec a 6= 0, tels que pour tout réel x, f (x) = ax2 + bx + c
– fonctions puissances d’exposant entier naturel :
f est une fonction puissance d’exposant entier naturel, s’il existe un
entier naturel non nul n, tel que pour tout réel x, f (x) = xn
– fonction racine, fonctions circulaires, et autres :
√
x
1
f : x 7→
x
1
f : x 7→ 2
x
f : x 7→
f : x 7→ sin (x)
f : x 7→ cos (x)
Exercice 2.24. Écrire les fonctions suivantes comme résultat d’opérations sur
les fonctions de référence :
√
f: x →
7
cos
x+3
f : x 7→ x2 + 3x + 1 + x sin (x)
x sin (2x − 1)
f : x 7→ √
x2 − 3x + 1
√
f : x 7→ (2x − 1) 3x + 2 + cos (x − 5)
CHAPITRE 2. OUTILS D’ALGÈBRE ET D’ANALYSE
2
14
Courbes représentatives
Définition 2.25 (repère du plan). On appelle repère du plan tout triplet
(O ; ~ı, ~) avec O un point du plan et ~ı et ~ des vecteurs non colinéaires du
plan.
On dit que le repère (O ; ~ı, ~) est orthogonal si ~ı⊥~.
On dit que le repère (O ; ~ı, ~) est orthonormal, s’il est orthogonal et si k~ık =
k~k = 1
Définition 2.26 (courbe représentative d’une fonction). On considère le
plan rapporté à un repère quelconque (O ; ~ı, ~). Soit f une fonction de R vers
R, dont l’ensemble de définition est Df .
On appelle courbe représentative de f dans le repère (O ; ~ı, ~), l’ensemble
des points de couple de coordonnées (x, f (x)) où x ∈ Df .
On notera souvent cette courbe (Cf ), avec
(Cf ) = {M (x, f (x))/ x ∈ Df } = {M (x, y)/ x ∈ Df et y = f (x)}
Il y a autant de courbes représentatives que de repères possibles.
Définition 2.27. On dit qu’une courbe représentative d’une fonction est
symétrique par rapport à un point ou bien une droite, si le symétrique, par
rapport à ce point ou cette droite de tout point de la courbe, appartient à la
courbe. On dit alors respectivement que le point ou la droite est un centre
ou un axe de symétrie de cette courbe.
Définition 2.28. Soit f une fonction de R vers R et dont l’ensemble de
définition est Df .
– f est dite paire si pour tout x ∈ Df :
i). −x ∈ Df
ii). f (−x) = f (x)
– f est dite impaire si pour tout x ∈ Df :
i). −x ∈ Df
ii). f (−x) = −f (x)
3
Sens de variation
Comment évolue l’image de la variable réelle x en fonction de cette variable ?
Soit f une fonction de R vers R, définie sur un ensemble non vide E.
(Attention : La nature de E peut avoir une influence.)
CHAPITRE 2. OUTILS D’ALGÈBRE ET D’ANALYSE
15
– soit f n’est pas monotone dans E : il existe quatre réels a, b, c et d
dans E avec a < b et f (a) < f (b) et c < d et f (c) > f (d)
– soit f est monotone dans E : dans le cas contraire
Définition 2.29. Soit f une fonction de R vers R, définie sur un ensemble
non vide E.
– f est dite monotone croissante (respectivement décroissante) sur E si
pour tous a et b de E tels que a < b, on a f (a) 6 f (b) (respectivement
f (a) > f (b)).
– f est dite monotone strictement croissante (respectivement strictement
décroissante) sur E si pour tous a et b de E tels que a < b, on a
f (a) < f (b) (respectivement f (a) > f (b)).
– f est dite constante sur E si pour tous a et b de E, f (a) = f (b), ou
de manière équivalente s’il existe un réel λ, tels que pour tous x de E,
f (x) = λ
Remarque 2.30. Une fonction constante sur un ensemble non vide E est
monotone sur E mais non strictement monotone.
Théorème 2.31. Soit f une fonction de R vers R, définie sur un ensemble
non vide E. Si f est croissante et décroissante sur E, alors f est constante.
Démonstration. On reprend les notations du théorème précédent. Admettons que f à la fois croissante et décroissante. Soit a et b de E.
1er cas : Suppsons que a = b. On a bien évidemment f (a) = f (b).
2e cas : Supposons que a < b. On a f (a) 6 f (b) car f est croissante sur E, et
on a f (a) > f (b) car f est croissante sur E. Donc f (a) = f (b).
3e cas : Supposons que b < a. On a f (b) 6 f (a) car f est croissante sur E, et
on a f (b) > f (a) car f est croissante sur E. Donc f (a) = f (b).
Donc pour tous a et b de E, on a f (a) = f (b). Alors f est constante sur E.
Question 2.32. Soit f une fonction de R vers R, définie sur deux ensembles
non vides E1 et E2 . Si f est croissante sur E1 et E2 , f est-elle croissante sur
E1 ∪ E2 ?
Théorème 2.33. Soit λ un réel. Soit f une fonction de R vers R, strictement
croissante (respectivement strictement décroissante) sur ]−∞ ; λ[, strictement croissante (respectivement strictement décroissante) sur ]λ ; +∞[.
f est strictement croissante (respectivement strictement décroissante) sur R.
Démonstration. À venir
CHAPITRE 2. OUTILS D’ALGÈBRE ET D’ANALYSE
16
Théorème 2.34. Soit E un ensemble non vide de réels, non réduit à un
singleton, et f une fonction de R vers R, définie sur E. Si f est monotone
sur E, sans être strictement monotone sur E, alors il existe deux réels a et b
distincts, dans E tels que f (a) = f (b).
Démonstration. À venir
Théorème 2.35. Soit E un ensemble non vide de réels et f une fonction
de R vers R, strictement monotone sur E. Alors tout réel a a au plus un
antécédent par f dans E.
Démonstration. À venir
Théorème 2.36. La fonction f : x 7→ x est strictement croissante sur
R.
Démonstration. Soit a et b des réels, avec a < b. On a f (a) = a et f (b) = b.
Comme a < b, alors f (a) < f (b). Donc pour tous réels a et b, si a < b,
f (a) < f (b). Donc f est strictement croissante sur R.
Théorème 2.37. La fonction f : x 7→ x2 est strictement décroissante
sur R− et strictement croissante sur R+ .
Démonstration. À venir
Théorème 2.38. La fonction f : x 7→ x3 est strictement croissante sur
R.
Démonstration. À venir
Théorème 2.39. Soit a et b des réels. La fonction f : x 7→ ax + b est
strictement croissante sur R si a > 0, strictement décroissante sur R si a < 0,
et constante sur R si a = 0.
Démonstration. À venir
Théorème 2.40. La fonction f : x 7→
sur R+ .
√
x est strictement croissante
Démonstration. À venir
1
Théorème 2.41. La fonction f : x →
est strictement décroissante
7
x
sur R∗− et strictement décroissante sur R∗+ .
Démonstration. À venir
CHAPITRE 2. OUTILS D’ALGÈBRE ET D’ANALYSE
17
Théorème 2.42. Soit n ∈ N∗ . Si n est pair, la fonction f : x 7→ xn
est strictement décroissante sur R− et strictement croissante sur R+ , et la
1
fonction g : x 7→ n est strictement croissante sur R∗− et strictement
x
décroissante sur R∗+ .
Si n est impair, la fonction f : x 7→ xn est strictement croissante sur
1
R, et la fonction g : x 7→ n est strictement décroissante sur R∗− et
x
strictement décroissante sur R∗+ .
Démonstration. Résultat admis.
Addition
Multiplication par une constante réelle λ
Multiplication de deux fonctions
Passage à l’inverse
Division de fonctions
Table des matières
A
Logique
1
1 Logique élémentaire
2
B
4
Algèbre
2 Outils d’algèbre et d’analyse
I
Calcul numérique et algébrique . . . . . . .
1
Vocabulaire et notation . . . . . . . .
2
Théorèmes, propositions et résultats
3
Expressions polynomiales du premier
degré (à une variable réelle) . . . . .
4
Racines, puissances et valeur absolue
II
Équations . . . . . . . . . . . . . . . . . . .
1
Concepts . . . . . . . . . . . . . . . .
2
Stratégies de résolution . . . . . . . .
3
Systèmes . . . . . . . . . . . . . . . .
III Fonctions et applications . . . . . . . . . . .
1
Concepts . . . . . . . . . . . . . . . .
2
Composition de fonctions . . . . . . .
IV Les fonctions en analyse . . . . . . . . . . .
1
Opérations sur les fonctions . . . . .
2
Courbes représentatives . . . . . . .
3
Sens de variation . . . . . . . . . . .
18
. . . . . . . . .
. . . . . . . . .
. . . . . . . . .
et du deuxième
. . . . . . . . .
. . . . . . . . .
. . . . . . . . .
. . . . . . . . .
. . . . . . . . .
. . . . . . . . .
. . . . . . . . .
. . . . . . . . .
. . . . . . . . .
. . . . . . . . .
. . . . . . . . .
. . . . . . . . .
. . . . . . . . .
.
.
.
5
5
5
6
.
.
.
.
.
.
.
.
.
.
.
.
.
6
9
10
10
10
10
11
11
11
12
12
14
14