Feuille 3 - IMJ-PRG

Université Pierre & Marie Curie Licence de mathématiques 3
UE 3M210 Analyse fonctionnelle Année 2015–16
Feuille 3. Espaces de Hilbert (1)
Exercice 1.
a) Soit (E, k·k)un espace vectoriel normé. Montrer que c’est un espace pré-hilbertien si et seulement
si
∀x, y ∈E, kx+yk2+kx−yk2= 2kxk2+ 2kyk2.
On appelle cette propriété l’identité du parallélogramme.
b) Soit (H, k·k)un espace pré-hilbertien. Montrer que pour x, y ∈Hon a
kxk=kyk ≤ 
x+y
2
=⇒x=y.
Comment peut on interpréter géométriquement ce résultat ?
c) Soit (X, A, µ)un espace mesuré. On suppose qu’il existe deux parties mesurables A1, A2∈ A
qui sont disjointes et de mesure finie non-nulle. Montrer que Lp(µ)n’est pas un Hilbert si p6= 2.
Exercice 2. (Base de Walsh). Soit n≥1et Ωn={−1,1}n, que l’on muni de la mesure de comptage
normalisée, µn({x}) = 1
2n, c’est-à-dire, pour f: Ωn→R,
Zfdµn=1
2nX
x∈{−1,1}n
f(x1, . . . , xn).
a) Montrer que L2(µn) = RΩn, et que c’est un espace de dimension finie que l’on précisera.
b) Montrer que µn=µ1⊗. . .⊗µ1où µ1est la mesure sur {−1,1}définie par µ1({1}) = µ1({−1}) =
1
2.
c) Pour pour une partie S⊂ {1, . . . , n}=: [n]une partie non vide, on introduit χS: Ωn→Rqui
est défini par χS(x) = Qi∈Sxi.Pour Svide on pose χ∅≡1. Montrer que {χS, S ⊂[n]}forme
une base orthonormée de L2(µ).
Remarque : on vérifie aussi que les {χS, S ⊂[n]}sont les caractères sur le groupe (abélien) multiplicatif
({−1,1}n,×). Ils forment le groupe dual (que l’on peut aussi identifier à (P([n],∆)). On vient de voir
un exemple de groupe dual G∗d’un groupe abélien (fini) Gqui forme une base orthonormée de L2(G).
Exercice 3. (Partition finie, moyennes.) Considérons un espace de probabilité (Ω,A, µ). Supposons
que A1, . . . , ANsoit une partition de Ωen ensembles de la tribu A, tels que µ(Aj)>0pour tout
j= 1, . . . , N. Soit Fl’ensemble des fonctions (réelles) qui sont constantes sur chaque ensemble de la
partition.
a) Soit Cl’ensemble des réunions finies d’ensembles Aj,j= 1, . . . , N. Montrer que Cest une sous
tribu de A, et qu’une fonction A-mesurable est C-mesurable si et seulement elle appartient à F.
b) Montrer que Fest un sous espace vectoriel de L2(Ω,A, P ).
c) Montrer que la famille de fonctions fj=µ(Aj)−1/21Aj, j = 1, . . . , N est une base orthonormée
de F.
d) Donner une formule pour la projection d’une fonction f∈L2(Ω,A, P )sur F.
Exercice 4. Soit fune fonction mesurable sur R,2π-périodique et telle que la restriction de fà
[0,2π]soit intégrable. Montrer que pour tout T∈Ron a
Z[T,T +2π]
f(s)ds =Z[0,2π] f(t)dt.
1

Exercice 5. On travaille sur [0,2π]muni de la mesure de Lebesgue dt normalisée pour être une
probabilité, i.e. Il est facile de voir que la famille de fonctions {en}n∈Zoù en(t) = eint, est une famille
orthogonale de L2([0,2π]). On notera, pour fintégrable sur [0,2π],
cn(f) = hen, fi=Z[0,2π] f(t)e−int dt.
Le but de cet exercice est de vérifier que la famille {en}n∈Zest base hilbertienne, c’est-à-dire que l’espace
qu’elles engendrent (qui s’appelle l’espace des polynômes trigonométriques) est dense dans L2([0,2π]).
Par un résultat de cours, il suffit de montrer que pour toute fonction f∈L2([0,2π]), si
∀n∈Z, cn(f)=0,(∗)
alors f= 0 dans L2(m), i.e. f= 0 p.p. Commentaire : une méthode classique pour montrer cela est de
démontrer d’abord la densité des fonctions continues dans L2, puis dans le cas des fonctions continues,
utiliser le théorème de Weierstrass, que l’on peut montrer en utilisant la convolution avec le noyau de
Dirichlet. Nous allons utiliser ici une méthode directe qui ne présuppose aucun résultat préalable.
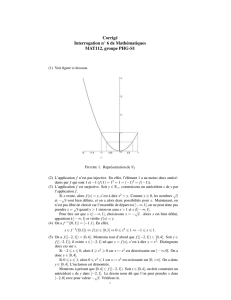
a) Dans cette question, on suppose que f∈L2[0,2π]est une fonction réelle vérifiant (∗). On va
supposer qu’il existe h > 0(h<π)et α > 0pour lesquels on a f≥αsur [π−h, π +h], et
aboutir à une contradiction.
i) Pour n∈Non introduit Pn(t) = 1 + cos(t−π)−cos(h))n.Montrer que hPn, fi= 0 pour
tout n∈N.
ii) Discuter, suivant la valeur de t∈[0,2π], la limite de Pn(t)lorsque n→+∞.
iii) Montrer que, lorsque n→+∞,
Z[0,π−h]
f(t)Pn(t)dt →0et Z[π+h,2π] f(t)Pn(t)dt →0.
iv) Montrer que, lorsque n→+∞,
Z[π−h,π+h]
f(t)Pn(t)→+∞.
v) Conclure.
b) Montrer que toute fonction continue sur [0,2π]à valeurs réelles qui vérifie (∗)est identiquement
nulle.
Indication : on pourra supposer que fest non-identiquement nulle, prolonger la fonction à R
par périodicité et faire une translation pour se ramener à la situation précédente.
c) Montrer que tout fonction continue (à valeurs complexe) sur [0,2π]qui vérifie (∗)est identique-
ment nulle.
Indication : on pourra remarquer que si fvérifie (∗)alors fvérifie aussi (∗).
d) Soit f∈L2([0,2π]avec R[0,2π]f(t)dt =c0(f)=0. Montrer que la fonction
F(x) = Z[0,x] f(t)dt.
est continue, et que pour n∈Z,n6= 0 on a
cn(F) = −i
ncn(f).
e) En déduire que si fvérifie (∗)alors la fonction Fde la question précédente est constante (donc
nulle) et que pour tout x, y ∈[0,2π],
Z]x,y[
f(t)dt = 0.
f) Conclure.
2