2014-2015 OS4 Evolution

74
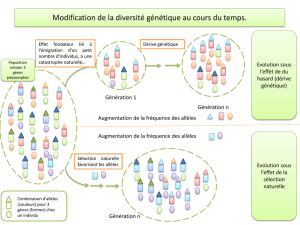
7 L A GÉNÉTIQUE DES POPULATIONS
Une population représente un groupe d’organismes de la même espèce, à un moment donné et à un
endroit donné. Une population peut être isolée des autres populations de la même espèce et n’échanger
que rarement du matériel génétique avec elles. Cet isolement touche particulièrement les populations
habitant des îles éloignées, des lacs fermés ou des chaînes de montagnes entrecoupées de terres basses.
Mais, les populations ne restent pas toujours isolées et n’ont pas nécessairement des limites précises.
7.1 Patrimoine génétique
Le patrimoine génétique (« pool génétique ») d’une population comprend l’ensemble des allèles
occupant tous les loci de tous les individus de la population. Chez une espèce diploïde, chaque gène
figure deux fois dans le génome d’un individu, lequel est soit homozygote (allèles identiques) soit
hétérozygote (allèles différents) pour ces allèles. Si tous les membres d’une population portent deux
allèles identiques (homozygotes), on parle de fixation de l’allèle dans le patrimoine génétique. La
plupart du temps, il existe deux allèles ou plus pour un gène, et chacun présente une fréquence relative
(fréquence allélique) dans le patrimoine génétique. Comment les facteurs du milieu agissent-ils sur la
fréquence des allèles d'une population ?
Voici l’exemple de la phalène du bouleau :
La phalène du bouleau (Biston betularia) est un papillon
nocturne fréquent en Europe du nord. Ils se reposent le jour
les ailes étalées sur les écorces claires des bouleaux. La
phalène du bouleau se rencontre sous deux formes, une
forme de couleur claire dit typica et l'autre sombre dit
carbonaria ou mélanique. Ces variations de couleur sont
dues à la quantité de mélanine présente dans les ailes du
papillon adulte.
A partir du XIX
e
siècle, les entomologistes observent que la
forme sombre devient plus fréquente à proximité des villes
industrielles d'Angleterre; observée pour la première fois en
1848 dans la région de Manchester, cette forme sombre est
devenue largement majoritaire en 1895 dans cette même région (plus de 98% de la population). Cette
observation est alors rapprochée d'un autre phénomène : en raison de la pollution atmosphérique par
les résidus de combustion du charbon, les troncs et les branches des arbres devenaient plus sombres (à
la fois par les dépôts de fumée et probablement aussi par la disparition des lichens plus clairs qui les
recouvraient).
Cette variété de phénotypes résulte de l'expression de deux allèles contrôlant la couleur des ailes. Au
départ, l'allèle codant la couleur claire est le plus fréquent dans la population bien que
l'allèle « mutant » existe. Dans les régions industrielles, l'écorce des bouleaux est recouverte de suie.
La population de phalènes montre alors une majorité d'individus sombres et des formes claires rares :
c'est le "mélanisme industriel". La fréquence de l'allèle donnant la couleur sombre augmente tandis
que la fréquence de l'allèle donnant la couleur claire diminue. Or, à partir de la fin des années 1960,
ce phénomène s'inverse. La forme typica redevient fréquente. C'est aussi à cette période que des
efforts sont mis en place pour améliorer la qualité de l'air en Grande-Bretagne, efforts qui se traduisent
notamment par une diminution des dépôts de pollution atmosphérique sur les troncs d'arbres.

75
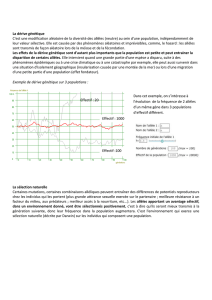
Voici ci-contre la distribution des fréquences des
deux formes vers la fin du XIXème siècle. On
remarque que la forme mélanique est majoritaire dans
les régions industrielles du nord et de l'est, tandis que
la forme claire prédomine dans les régions rurales du
sud-est. Dans les campagnes, la population de
phalène montre toujours des individus clairs
majoritaires. On peut supposer qu'il s'agit d'une
sélection visuelle en rapport avec la prédation. En
effet, les papillons sombres dans les zones
industrielles, peu visibles sur les supports sombres
échappent à la prédation des oiseaux. Les individus
sombres survivant vont se reproduire. La fréquence
de l'allèle donnant la couleur sombre va donc
augmenter dans la population. Les papillons clairs,
eux, n'échappent pas à la prédation car ils se
détachent sur les écorces noires.
C'est la population qui évolue et non l’individu.
Cette évolution est liée à deux conditions : premièrement, la population initiale doit être composée de
phénotypes variés d'origine génétique. Deuxièmement, cette variation phénotypique engendre une
aptitude à la survie ou la reproduction.
La prédation n'est pas le seul facteur sélectif, il peut s'agir de résistance aux maladies ou à des
insecticides, antibiotiques, de conditions physico-chimiques du milieu (température, salinité, taux
d’oxygène).
A l’échelle la plus réduite, l’évolution consiste en une modification, au cours de générations
successives, des fréquences des allèles dans une population ; une telle modification du patrimoine
génétique de la population est appelée microévolution.
On ne peut considérer des individus uniques en tant que représentants d’une espèce. Aucun individu
ne peut porter toutes les caractéristiques de l’espèce. Celle-ci est décrite par la somme des caractères
présents dans une population.
L’individu peut être considéré comme l’unité de sélection, le gène comme l’unité d’hérédité et la
population comme l’unité d’évolution

76
7.2 La loi de Hardy-Weinberg
La loi de Hardy-Weinberg a été développée en 1908 par un Anglais, Godfrey Hardy (1877 – 1947) et
un Allemand, Wilhelm Weinberg (1862 – 1937). Cette loi prédit que lorsqu’il n’y a pas d’agents
évolutifs à l’œuvre, la population n’évolue pas car la fréquence des allèles ainsi que la fréquence des
génotypes (déterminé par ces allèles) demeurent constantes de génération en génération. En
conséquence, le brassage des allèles résultant de la méiose et des aléas de la fécondation n'ont pas
d'effet sur la composition génétique globale d'une population.
7.2.1 Démonstration de la loi Hardy-Weinberg
Mise en situation : Une population mère de fleurs sauvages : 320 homozygotes rouges (RR), 160
hétérozygotes rouges (Rr) et 20 homozygotes blancs (rr) «total de 500 individus».
Phénotype
s
Génotypes
Fréquence des génotypes
dans la population
Fréquence des allèles
dans la population mère
p : fréquence de R = 0,8 q : fréquence de r = 0,2
Patrimoine génétique de
la population parentale
Nombre d’allèles dans le
pool génique (total = 1000)
La somme des fréquences
des allèles est 1
Gamètes mâles Gamètes femelles
Fréquence des génotypes
Fréquence des allèles
Patrimoine génétique de
la population fille
Tous les individus de la population mère se
reproduisent et font des gamètes.
La fréquence des allèles R et r dans les gamètes est
la même que celle de la population mère.
L’union des gamètes se produit au hasard et tous,
ont la même chance d’être fécondés.
Les fréquences des génotypes
ainsi que celle des allèles «de la
population fille» sont les mêmes
que celles de la population mère.
La population n’a pas évolué.

77
En résumé, Lorsqu’il n’y a pas d’agents évolutifs à l’œuvre, une population maintient sa structure
génétique de génération en génération.
En d’autres mots, les fréquences des allèles et des génotypes de la population se maintiennent de
génération en génération.
On dit d’une population qui n'évolue pas qu’elle présente l'équilibre d'Hardy- Weinberg
(équilibre panmictique).
7.2.2 Généralisation de la loi de Hardy-Weinberg
Généralisation de la loi d’Hardy-Weinberg pour une population où deux allèles seulement sont
étudiés : A et a.
p est la fréquence de l'allèle A et q est la fréquence de l'allèle a
(p+q) x (p + q) = p2 AA + 2pq Aa + q2 aa = 1
En utilisant cette équation, on peut déterminer la fréquence d’un allèle, d’un génotype ou d’un
phénotype dans la population.
7.2.3 Application 1
Un bébé sur 25 600 souffre de phénylcétonurie au Québec, une maladie récessive (p). Supposons que
la population du Québec présente l’équilibre de Hardy-Weinberg ; combien de personnes sont
porteuses de la maladie ?
p2 PP + 2pq Pp + q2 pp = 1
La fréquence des homozygotes récessifs est : 1 / 25 600 = 0,000039
La fréquence du gène récessif q(p) est : √ 0,000039 = 0,0062449
La fréquence du gène dominant p(P) est : 1 - q(p) = 1 - 0,0062449 = 0,9937551
La fréquence des hétérozygotes est : 2 pq (Pp) = 2 (0,9937551 x 0,0062449) = 0,0124118
Donc 124 personnes 10 000 sont porteuses de la maladie au Québec.
Fréquence des
gamètes mâles Fréquence des
gamètes femelles Fréquence des
homozygotes
dominants
Fréquence des
hétérozygotes Fréquence des
homozygotes
récessifs
Fréquence des génotypes de la génération fille
Homozygotes
dominants Hétérozygotes Homozygotes
récessifs
P = santé
p = phénylcétonurie

78
7.2.4 Application 2
Chez le bétail Shorthon, trois génotypes sont possibles :
RR : animaux rougeâtre RR’ = animaux rouans R’R’ = animaux blancs
Une population de Californie contient 324 rougeâtres, 432 rouans et 144 blancs. Supposant qu’elle
présente l’équilibre de Hardy-Weinberg, quelle est la fréquence des gènes dans son pool génétique ?
p2 RR + 2pq RR’ + q2 R’R’ = 1
On peut utiliser les homozygotes rougeâtres ou blancs pour le calcul mais pas les hétérozygotes rouans
qui contiennent les 2 allèles à la fois.
Prenons les blancs :
La fréquence des animaux blancs est : 144 blancs / 900 animaux = 0.16
La fréquence de l’allèle est : R’ = √ 0 .16 = 0.4
La fréquence de l’allèle est : R = 1 - 0.4 = 0.6
7.3 Les conditions d’application de la loi d’Hardy-Weinberg
• Les individus de la population sont diploïdes.
• Les individus se reproduisent selon un mode sexué. (Cette loi suppose la rencontre des
gamètes.)
• Les couples se forment au hasard et tous ont la même chance de se reproduire.
IL N'Y A PAS D'AGENTS ÉVOLUTIFS À L'ŒUVRE DANS LA POPULATION.
• Pas de dérive génétique car la population est de grande taille. (Les lois de la probabilité
s'appliquent.)
• Pas de flux génétique. (Pas d'immigration de gènes ou d'émigration de gènes vers d'autres
populations qui pourraient changer le pool génique.)
• Pas de mutations qui feraient apparaître de nouveaux allèles.
• Pas de sélection naturelle qui pourrait favoriser la transmission de certains allèles à la
descendance au détriment des autres.
7.4 L’équilibre d’Hardy-Weinberg n’existe pas mais est utile
Modèle théorique qui n'existe pas dans la nature.
Impossible que toutes les conditions nécessaires à l'équilibre d'Hardy-Weinberg soient présentes en
même temps.
Modèle qui permet d'évaluer s'il y a de la microévolution dans une population.
On mesure la fréquence des allèles dans la population mère et l’on applique l'équation. Si la structure
génétique de la population fille s'écarte de celle prédite par la loi, alors on sait qu'au moins un agent de
l'évolution est à l'œuvre.
Homozygotes
dominants Hétérozygotes Homozygotes blancs
R = Rouge
R’ = Blanc