Cours7

Cours 7 : Exemples
I- Régression linéaire simple
II- Analyse de variance à 1 facteur
III- Tests statistiques

Le modèle de régression linéaire simple
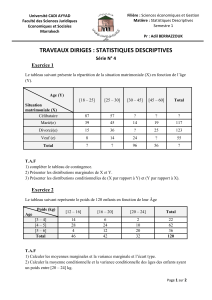
Exemple 1 : On cherche à expliquer les variations de y par celles d’une
fonction linéaire de x, i.e., à valider le modèle de RLS
où est une suite de variables aléatoires i.i.d. de moyenne nulle et de variance
>x=1:100; X=sample(x,30,replace=TRUE)
>Y=3+7*X+rnorm(30,0,100)
>regression=lm(Y~X); regression
Call:
lm(formula = Y ~ X)
Coefficients:
(Intercept) X
-30.26 7.42
i
ε
, 1,...,30.
ii i
yaxb i
ε
=
++ =
²
σ

Le modèle de régression linéaire simple
> plot(X,Y)
>text(40,600, substitute(y==a*x+b, list(a=regression$coef[2],
b=regression$coef[1])))
> lines(X,regression$fitted.values)
> M=locator(); v=locator()
> segments(0,M$y,M$x,M$y)
> arrows(M$x,M$y,M$x,v$y,angle=30, code=3)
> segments(M$x,v$y,0,v$y,lty=2)
> text(0,350, "yi",col="red")
> text(0,200, "^yi",col="red")
> text(25,250, "ei",col="red")
> title("nuage de points et droite de regression")

Le modèle de régression linéaire simple

Le modèle de régression linéaire simple
>names(regression)
[1] "coefficients" "residuals" "effects" "rank"
[5] "fitted.values" "assign" "qr" "df.residual"
[9] "xlevels" "call" "terms" "model«
coefficients (ou coef) : estimations des paramètres
fitted.values (ou fitted): valeurs estimées
Residuals (ou res) : résidus
df.residual : nombre de ddl des résidus (n-2)
ˆ
ˆet ab
ˆ
iii
eyy
=
−
ˆi
y