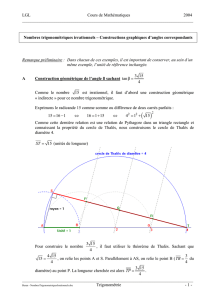
énoncé

Z
YZX
k∈N∗UkkZ{−1,1}
P(Uk= 1) = P(Uk=−1) = 1/2Uk
α∈]0, π[n∈N∗
Yn=
n
X
k=1
UkXn=iαYn
Y0= 0 X0= 1
Y1Y2
U1n∈N∗
Yn
n∈N∗
∀j∈[[0, n]],P(Yn=−n+ 2j) = n
j1 2n
Xn
Xn
n∈N
Xn+1 =(iαXn1/2
−iαXn1/2
k∈Z P(Xn+1 =ikα)Xn=
ijα
E(Xn)E(Xn+1)
N>3α=2π
N·ω=iα =
2iπ/N UNz∈CzN= 1
ωNUNωU3U5
X1(Ω) X2(Ω) X3(Ω) ω
Xn(Ω) n N = 5

n∈NZnn
Zn=
P(Xn= 1)
P(Xn=ω)
P(Xn=ωN−1)
A∈ MN(R)n∈NZn+1 =AZn
J∈ MN(R)Vk∈ MN,1(R)
J=
0 1 0 . . . 0
0 0 1
0
0. . . . . . 0 1
1 0 . . . 0 0
∀k∈[[0, N −1]], Vk=
1
ωk
ω2k
ω(N−1)k
VkJ
V0V1
t
JVkA P ∈N(R)D∈ MN(R)
P−1AP =D P −1
A1
1DnAnn+∞
P V0P−1Z0
k∈[[0, N −1]] P(Xn=ωk)−→
n→+∞
1
N·
a, b ∈N
a b
n∈N∗n
Zn
Z
n α

E n
u∈ L(E)
y∈E z ∈E x ∈E <u(x)|y>=<x|z>
u∗(y) = z
∀x, y ∈E, <u(x)|y>=<x|u∗(y)> .
u∗E E u
u∗
u1, u2∈ L(E)λ∈R(λu1+u2)∗=λu∗
1+u∗ 2
u7→ u∗L(E)
u∗
u x 7→ λx
u
u
u
<u(x)|y>=<x|v(y)>
EE
<x|y> X Y
x y E E
FEMat(u∗,F) = t (Mat(u, F))
u r E= (e1, ..., en)E
ei
n
P
i=1
ku(ei)k2=r
v∈ L(E)EE(v) =
n
P
i=1
<v(ei)|ei>
E F E w ∈ L(E)
n
X
i=1
kw(ei)k2=
n
X
i=1
kw(fi)k2.
u r
n
P
i=1
ku(ei)k2=rEu

R∈R[X]t7→ R(t)−tR+
n∈NIn=Z+∞
0
tn−tdt
In
P, Q ∈E=R[X]<P |Q>=Z+∞
0
P(t)Q(t)−tdt
<|> E
E
1
n∈N Rn−1[X]Rn[X]
(P0, P1, P2, P3)R3[X]
ϕ(a, b, c) = Z+∞
0t3−(at2+bt +c)2−tdt
(a, b, c)R3
ψ(a, b, c) = Z+∞
0t3−(at2+bt +c)−tdt
n∈Nt∈RQn(t) = (−1)n t (tn−t)(n)
n
Qn
Qn
Qkk63Qnn∈N
n∈N∗QnRn−1[X]
kQnk2
QnPn
Pn
n]0,+∞[
Qnn]0,+∞[
<X k|Pn>ZT
0