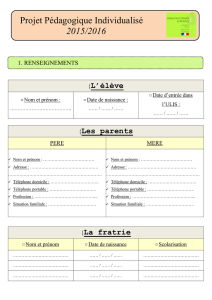
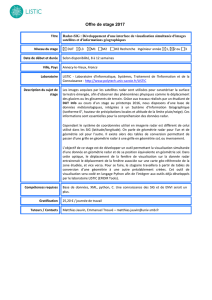
Géométrie analytique : Juillet 2013. Série 1 NOM Prénom

Géométrie analytique : Juillet 2013. Série 1
NOM Prénom :
Numéro :
Question 3 : (25%)
Soit une sphère S de rayon 5 centrée au point (x,y,z)=(1,0,0) et un plan P d’équation cartésienne x + 2y+z
=2. L’intersection du plan et de la sphère est un cercle. Soit O le centre de ce cercle. Soit D la droite
passant par O et perpendiculaire au plan P. Donnez les coordonnées cartésiennes des points d’intersection
entre la droite D et la sphère S.

Géométrie analytique : Juillet 2013. Série 1
NOM Prénom :
Numéro :
Question 4 : (25%)
Soit une parabole P d’équation cartésienne y=a x2 + b. Soit une droite D passant par l’origine et
tangente à la parabole en un point Q. L’on fait varier a, tandis que b reste constante. Quel est le lieu
géométrique de Q ? Si vous utilisez une formule toute faite concernant la tangente à une parabole,
vous devez la démontrer.

Géométrie analytique : Juillet 2013. Série 2
NOM Prénom :
Numéro :
Question 3 : (25%)
Soit un système de coordonnées cartésiennes XYZ. Soit une sphère S de rayon 4 qui
présente un seul point de contact P avec le plan XY. Soit une droite D passant par l’origine
et par le centre de la sphère, et dont les points satisfont à x=y. Soient A et B les deux points
d’intersection de la droite avec la sphère. La distance de B à l’origine est le double de celle
de A à l’origine. Donnez les coordonnées cartésiennes du point P.

Géométrie analytique : Juillet 2013. Série 2
NOM Prénom :
Numéro :
Question 4 : (25%)
Soit un repère cartésien XY. Soit une parabole A d’axe Y, dont le sommet est en (x,y)=(0,0)
et dont les autres points satisfont à y>0. Soit une parabole B, correspondant à une version
translatée de A, avec un sommet en (x,y)=(4,0). Ces paraboles se coupent à angle droit (les
tangentes au point d’intersection sont orthogonales). Donnez les équations cartésiennes de
ces deux paraboles.

Géométrie analytique : Septembre 2013.
NOM Prénom :
Numéro :
Question 3 : (25%)
Soient deux cibles situées en (x,y)=(-2,0) et (x,y)=(2,0). Un radar, situé en un endroit inconnu du plan XY,
envoie une impulsion et reçoit en retour des impulsions en provenance des deux cibles. Entre les deux
impulsions reçues, il y a un décalage temporel de 2/c secondes, où c est la vitesse de la lumière. Les distances
sont données en mètres et c en mètres par secondes. Quel est le lieu des positions possibles du radar (son type et
son équation cartésienne) ?
Pour information, le temps de parcours aller-retour d’une impulsion entre le radar et une cible correspond à 2d/c
où d est la distance entre le radar et la cible. Commencez par faire un dessin et par relier les instants des
impulsions reçues avec la géométrie du problème.