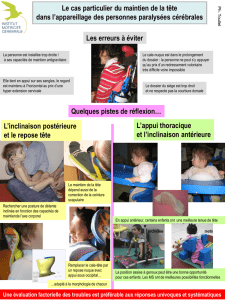
polaires de ce planeur en virage
60 80 100 120 140 160 180 200 220
−3.5
−3
−2.5
−2
−1.5
−1
−0.5
0Polaire de vitesse (ASW 28 − 38.1kg/m²)
Vi
Vz
2
2
0 0.01 0.02 0.03 0.04 0.05 0.06 0.07
0
0.2
0.4
0.6
0.8
1
1.2
1.4
Cx
Cz
Polaire aérodynamique (ASW 28)
Cxmin = 0.092
Czmax = 1.35
CzF inesse max = 0.74
fmax = 44
6
7
8
9
10
11
12
13
14
15
16
17
18
19
1
/
19
100%
