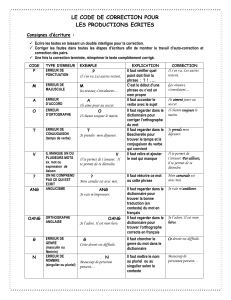
La division

C
C
Ch
h
ha
a
ap
p
pi
iit t
tr
r
re
e
e
1
1
10
0
0
D
D
Di
i
iv
v
vi
i
is
s
si
i
io
o
on
n
ns
s
s
I. Multiples et diviseurs
Activité :
Ecris les multiples de 7 :
Multiples de 25 :
Exemple : les multiples de 11 sont 0 ; 11 ; 22 ; 33 ; 44 ; 55 …
Vocabulaire :
 44 est un multiple de 11
 11 est un DIVISEUR de 44
 44 est DIVISIBLE PAR 11
Activité (tableaux de nombres)
Définition
1. Soit n un nombre entier. Les MULTIPLES de n sont :
n  0 ; n  1 ; n  2 ; n  3 ; n  4 ; n  5 ; n  6 ; … etc
0
n

Règle 1
Un nombre entier est multiple de 2
si son chiffre des unités est 0 ou 2 ou 4 ou 6 ou 8.
On dit que c’est un NOMBRE PAIR
divisible par 2
Règle 2
Un nombre entier est multiple de 3
si la somme de ses chiffres est dans la table de 3.
divisible par 3
Règle 3
Un nombre entier est multiple de 5
si son chiffre des unités est 0 ou 5.
divisible par 5
Règle 4
Un nombre entier est multiple de 9
si la somme de ses chiffres est dans la table de 9
divisible par 9
Règle 5
Un nombre entier est multiple de 4
si le nombre formé par les deux derniers chiffres est dans
la table de 4
divisible par 4

Exemple : 412 est-il divisible par 4 ?
Oui car 12 (le nombre formé par les 2 derniers chiffres) est dans la table
de 4.
II. La division euclidienne
« C’est qui, Euclide ? »
Activité : l’araignée
Définition
Soient a et b deux nombres entiers naturels (avec b ≠ 0).
Effectuer la division euclidienne de a par b ça veut dire trouver les 2
nombres entiers q et r tels que :
a = (b  q) + r
r < b
Règle 6
Un nombre entier est multiple de 10
si son chiffre des unités est 0.
divisible par 10
diviseur
reste
dividende
quotient
a
r
q
b
Bla bla bla bla bla bla bla bla Bla bla bla bla bla bla bla bla Bla bla bla bla bla bla bla bla Bla bla
bla bla bla bla bla bla Bla bla bla bla bla bla bla bla Bla bla bla bla bla bla bla bla Bla bla bla bla
bla bla bla bla Bla bla bla bla bla bla bla bla Bla bla bla bla bla bla bla bla Bla bla bla bla bla bla
bla bla Bla bla bla bla bla bla bla bla Bla bla bla bla bla bla bla bla Bla bla bla bla bla bla bla bla
Bla bla bla bla bla bla bla bla Bla bla bla bla bla bla bla bla Bla bla bla bla bla bla bla bla Bla bla
bla bla bla bla bla bla Bla bla bla bla bla bla bla bla Bla bla bla bla bla bla bla bla Bla bla bla bla
bla bla bla bla

Exemple : pose la division euclidienne 254 ÷ 11.
Cela veut dire que …
Exemples de problèmes pour cette division :
 Problème 1 : ….
 Problème 2 : ….
Remarque : lorsque le reste de la division est 0, cela veut dire que le
dividende est un multiple du diviseur
Exemple : avec 2700 divisé par 9
III. La division décimale
Division euclidienne
Exemple de problème :
Division décimale
Exemple de problème :
9 8 1
1 5
9 8 1
1 5
981 =

Technique pour poser une division décimale :
 Poser 54,4 ÷ 16
Ici le quotient est un nombre décimal
 Parfois, le quotient n’est PAS décimal :
Poser 1 ÷ 3
 Comment fait-on si le diviseur est un nombre décimal ?
Poser 39,92 ÷ 1,2
Cela à revient à poser …