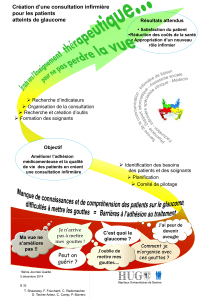
gouttes rebondissantes sur une surface vibree verticalement

Projet de physique expérimentale L3
- Mars 2010 -
zzz
GOUTTES REBONDISSANTES
SUR UNE SURFACE
VIBRÉE VERTICALEMENT
zzz
Lorène Champougny
Pierre Lidon
1

Table des matières
1 Dispositif expérimental 3
1.1 Matériel utilisé - Montage . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.2 Comment fabriquer des gouttes rebondissantes ? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.3 Premières observations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
2 Etude statistique de la durée de vie des gouttes 4
2.1 Protocole expérimental . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
2.2 Résultats et interprétation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
2.2.1 Durée de vie en fonction de l’amplitude et de la fréquence à rayon …xé . . . . . . . . . . . . . 4
2.2.2 Durée de vie en fonction du rayon à fréquence et amplitude …xées . . . . . . . . . . . . . . . . 6
2.3 Explication des phénomènes observés . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
3 Interactions entre gouttes 7
3.1 Montage expérimental . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
3.2 Interactions à deux gouttes - Potentiel d’interaction . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
3.2.1 Mode opératoire . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
3.2.2 Courbes de potentiel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
3.3 Phénomènes d’adhésion et de fusion des gouttes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
3.3.1 Temps d’adhésion entre deux gouttes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
3.3.2 Explications physiques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
3.4 Interactions à trois gouttes ou plus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
3.4.1 Cristaux de gouttes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
3.4.2 Autoorganisation des gouttes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
4 Discussion et perspectives 12
4.1 A propos de l’hypothèse de sphéricité et du rayon des gouttes... . . . . . . . . . . . . . . . . . . . . . 12
4.1.1 Discussion de l’hypothèse de sphéricité . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
4.1.2 Contrôle du rayon des gouttes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
4.2 A propos de l’étude statistique de la durée de vie des gouttes... . . . . . . . . . . . . . . . . . . . . . 13
4.3 A propos de l’étude de l’interaction entre gouttes... . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
Introduction
Lorsqu’une goutte de pluie heurte la surface d’une ‡aque d’eau, elle perd sa structure et se fond dans le reste du
liquide. Ce phénomène familier, appelé coalescence, peut cependant être empêché sous certaines conditions et pour
certains types de ‡uides. La goutte conserve alors sa forme et son individualité. C’est en étudiant l’instabilité de
Faraday - ces ondes gravito-capillaires qui apparaissent à la surface d’un ‡uide vibré verticalement - qu’Yves Couder
et son équipe ont observé la non coalescence de gouttes, dans le cas de ‡uides visqueux. Ce qui était au départ
un phénomène parasite s’est cependant révélé être un sujet d’étude à part entière. La survie d’une goutte est due
au fait que les rebonds renouvellent périodiquement le …lm d’air qui sépare la goutte de la surface du liquide. En
outre, ces gouttes qui semblent "rebondir" à la surface d’un ‡uide possèdent des propriétés remarquables : elles sont
notamment capables d’interagir entre elles, ou encore de se mouvoir spontanément lorsque l’amplitude d’excitation
est proche du seuil d’instabilité de Faraday (les gouttes sont alors appelées "marcheurs").
Dans le cadre des mini-projets du premier semestre, nous avions étudié certaines caractéristiques des instabilités
de Faraday. Dans la continuité de cette première approche, notre projet de physique expérimentale du second
semestre porte sur l’étude de propriétés des gouttes rebondissantes dans leur état "stationnaire", c’est-à-dire dans
des conditions où les gouttes sont immobiles (par opposition aux marcheurs qui se déplacent à la surface du ‡uide).
Nous nous sommes dans un premier temps intéressés à la durée de vie des gouttes, ce qui nous a permis de dégager des
zones de durée de vie maximale a…n de mener la deuxième partie de notre travail. Celle-ci concerne les interactions
entre gouttes : elle s’attache à déterminer le "potentiel d’intertaction" entre deux gouttes, puis à étudier plus
qualitativement les con…gurations adoptées par trois gouttes ou plus. La dernière partie, porte un regard critique
sur les résultats obtenus, ainsi que sur les méthodes expérimentales utilisées.
2

1 Dispositif expérimental
1.1 Matériel utilisé - Montage
Le montage utilisé est le montage classique pour obtenir l’instabilité de Faraday, schématisé sur la Figure 1.
Figure 1 - Schéma du montage expérimental
L’accéléromètre a un gain en tension G= 100 et son coe¢ cient de calibration vaut : = 10:3mV=g où
g= 9:81 m:s2est l’accélération gravitationnelle.
L’accéléromètre récupère l’accélération subie par une cellule carrée de côté 78 mm, remplie avec 20 mL de
‡uide, soit une hauteur de liquide de 3:3mm. Nous travaillons avec une huile de silicone dont les caractéristiques
sont les suivantes :
Masse volumique = 975 kg:m3
Viscosité = 500 cP o = 0:5P a:s
Tension de surface = 0:021 N:m1
1.2 Comment fabriquer des gouttes rebondissantes ?
A priori, l’existence et le comportement d’une goutte rebondissante dépendent des paramètres suivants :
- les caractéristiques du ‡uide utilisé, notamment sa viscosité et sa tension de surface
- l’amplitude d’excitation
- la fréquence d’excitation
- le rayon de la goutte.
On considérera dans toute l’étude que les gouttes produites demeurent sphériques et donc que l’on contrôle leur
rayon Rdirectement en contrôlant leur volume V=4
3R3, c’est pourquoi, dans la suite, on parlera indi¤éremment
de rayon ou de volume pour caractériser la taille d’une goutte. Cette hypothèse sera discutée plus en détail dans la
première section du paragraphe 4.
Nous avons choisi d’utiliser la même huile de silicone dans toute l’étude : ;  et seront donc des paramètres
…xés dans ce qui suit. L’accélération (ou, de manière équivalente à fréquence …xée, l’amplitude d’excitation) se règle
à l’aide de l’ampli…cateur et varie entre 1m:s2et 20 m:s2. La fréquence d’excitation est …xée par le générateur
basses fréquences (GBF) et va, dans notre étude, de 10 Hz à80 Hz .
Le rayon de la goutte est le paramètre de notre expérience le plus di¢ cile à contrôler. Nous avons testé plusieurs
méthodes de production de gouttes :
déposer les gouttes à la surface du liquide vibrant à l’aide d’une pipette Pasteur permet de former des
gouttes de rayon aléatoirement variable entre 1:3mm et 1:8mm. Cette technique est aisée à mettre en oeuvre
mais empêche un contrôle précis du rayon de la goutte. On l’utilisera lorsqu’il est nécessaire de produire
plusieurs gouttes dans un laps de temps court.
3

faire perler des gouttes le long d’un cheveu ou d’une aiguille permet, du moins théoriquement, de connaître
précisément le volume des gouttes formées, car celui-ci est relié au diamètre du cheveu (ou de l’aiguille)
employé(e), qui est mesurable par di¤raction. Cependant, en pratique, les goutelettes se forment sur le cheveu
en nombre incontrôlé et c’est …nalement une aggolmération de ces goutelettes, de volume assez quelconque,
qui …nit par former la goutte qui tombe.
déposer les gouttes à la surface à l’aide d’une pipette P20 (pipette utilisée en biologie) permet de prélever
de manière précise des volumes pouvant théoriquement aller de 0:1L à20 L: Cette technique nécessite plus
de soin mais fournit, une par une, des gouttes de rayon contrôlé. C’est elle que l’on utilisera pour réaliser des
études quantitatives, a…n de conserver le paramètre "taille de la goutte" constant.
1.3 Premières observations
En faisant varier les di¤érents paramètres qui régissent le comportement des gouttes rebondissantes sans ef-
fectuer de mesure, on peut déjà faire un certain nombre de remarques qualitatives qui pourront servir de pistes
pour la suite de l’étude.
Lorsque plusieurs gouttes sont présentes simultanément sur la surface du liquide, elles ont tendance à s’attirer
les unes les autres, à condition d’être su¢ samment rapprochées : il semble exister une distance caractéristique
d’interaction au delà de laquelle les gouttes ne "sentent" plus la présence les unes des autres.
Les gouttes en interaction s’attirent jusqu’à fusionner pour former une goutte plus grosse. Cette fusion peut
être instantanée ou bien temporairement retardée (dans le cas où les gouttes commencent par se "coller" l’une
à l’autre et fusionnent seulement après).
On peut également observer la …ssion de grosses gouttes (généralement obtenues par fusion) en plusieurs
gouttes plus petites.
A amplitude et fréquence d’excitation données, il semble exister un rayon pour lequel la stabilité de la goutte
est maximale.
A fréquence d’excitation et rayon …xés, il semble exister une amplitude pour laquelle la stabilité de la goutte
est maximale.
2 Etude statistique de la durée de vie des gouttes
2.1 Protocole expérimental
Une étude statistique de la durée de vies des gouttes en fonction des paramètres du problème nous a semblé
être une première étape naturelle, a…n de déterminer les conditions optimales pour observer d’autres propriétés des
gouttes rebondissantes. L’amplitude et la fréquence d’excitation étant plus commodes à faire varier, nous avons
commencé par faire une étude de stabilité à rayon …xé.
Pour une fréquence d’excitation donnée, nous avons fait varier l’amplitude et, pour chaque amplitude, mesuré
la durée de vie d’un échantillon statistique de 10 à20 gouttes de volume …xé V= 8 L: Les gouttes étaient
systématiquement seules dans la cellule, a…n que l’interaction entre gouttes (bien qu’apparemment négligeable
lorsqu’elles sont éloignées l’une de l’autre) n’introduise aucun biais. Nous avons répété ce procédé pour les fréquences
f= 10 Hz,f= 20 Hz; f = 40 Hz; f = 60 Hz et f= 80 Hz:
2.2 Résultats et interprétation
2.2.1 Durée de vie en fonction de l’amplitude et de la fréquence à rayon …xé
La Figure 2 regroupe les résultats statistiques obtenus pour la durée de vie en fonction de l’amplitude pour
les cinq valeurs de la fréquence citées ci-dessus.
Pour une fréquence et une accélération données, le carré rouge représente la durée de vie moyenne des gouttes,
les tirets verts indiquent la valeur moyenne à laquelle on a ajouté ou retranché l’écart-type, les croix bleues sont
les valeurs e¤ectivement observées lors de l’expérience. Il est important de remarquer que l’axe des ordonnées n’est
pas gradué de manière continue mais de manière discrète. Les entiers naturels indiqués représentent des intervalles
de durée de vie avec la correspondance suivante :
4

Numéro de l’intervalle de temps 0 1 2 3 4 5 6
Intervalle de temps (s) [0;1] [1;5] [5;10] [10;15] [15;20] [20;25] [25;30]
Numéro de l’intervalle de temps 7 8 9 10 11 12 13
Intervalle de temps (s) [30;35] [35;40] [40;45] [45;50] [50;55] [55;60] [60;+1[
Figure 2 - Durée de vie des gouttes en fonction de l’accélération à fréquence …xée.
Pour une fréquence donnée (le volume de la goutte étant toujours …xé à V= 8 L), on constate l’existence
d’une amplitude d’excitation telle que la stabilité des gouttes soit maximale. Les statistiques réalisées à f = 10 Hz
présentent même deux pics de stabilité. On peut supposer que l’on observerait également un deuxième pic de durée
de vie pour les fréquences supérieures à 10 Hz si le vibreur permettait d’obtenir des amplitudes d’excitation plus
grandes.
Le maximum est "bien marqué" (la durée de vie moyenne chute rapidement dès que l’on s’éloigne du maximum)
pour les fréquences inférieures à 40 Hz mais s’aplatit progressivement pour f= 60 Hz et f= 80 Hz.
Les valeurs des accélérations pour lesquelles la durée de vie est maximale sont regroupées dans le tableau
suivant :
Fréquence d’excitation (Hz)10 20 40 60 80
Accélération(s) de stabilité maximale (m:s2)6.0 - 17.5 4.0 6.0 10 12.5
On remarque également que la valeur de l’accélération pour laquelle les gouttes sont les plus stables augmente
avec la fréquence.
5