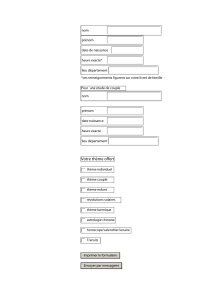
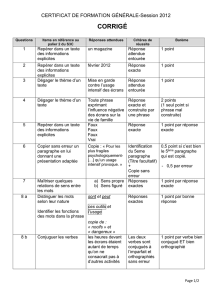
Formes différentielles (sur R#) 1. Formes différentielles et intégrales

Formes di¤érentielles (sur R2)
1. Formes di¤érentielles et intégrales curvilignes
a) Dé…nition et notation di¤érentielle, champ de vecteurs associé à une forme di¤érentielle
Soit Uun ouvert de Rn.
Dé…nition : Une forme di¤érentielle sur Uest une application de Udans L(R2;R):
Rappel :dx :U! L(R2;R)est l’application constante (x; y)7! x, et de même pour dy:
Alors toute forme di¤érentielle s’écrit sous la forme !(x; y) = a(x; y)dx +b(x; y)dy .
On dit que !est de classe Cnssi aet bsont de classe Cn:
Important :Toute forme di¤érentielle est naturellement associée à un champ vectoriel
!
A:U!Rn(x; y)7! a(x; y)
b(x; y):
On a ainsi !(x; y)(h; k) = D! A(x; y);(h; k)Epour tous (x; y)2Uet (h; k)2R2.
b) Intégrale curviligne
Dé…nition : Soit un arc de classe C1paramétré par : [; ]!R2t7! (x(t); y(t)).
On dé…nit R!=R
!((t))(0(t)) dt =R a(x(t); y(t)) x0(t) + b(x(t); y(t)) y0(t)dt:
Remarque : La notation R!est valide, car la valeur de R
!((t))(0(t)) dt ne dépend pas du choix de .
Remarque :R!est noté aussi R
!
A :! dl , appelé intégrale de !(ou travail de ! A) le long de :
On ainsi R
!
A :! dl =R
A((t)):0(t)dt:
2. Formes di¤érentielles exactes et fermées
a) Formes di¤ érentielles exactes
Dé…nition : On dit qu’une forme di¤érentielle !(x; y) = a(x; y)dx +b(x; y)dy dé…nie sur Uest exacte ssi il existe
une application fde classe C1de Udans Rtelle que !=df, c’est-à-dire ssi a(x; y)
b(x; y)!=0
B
@
@f
@x (x; y)
@f
@x (x; y)1
C
A.
Autrement dit, une forme di¤érentielle !est exacte ssi le champ ! Adérivé d’un potentiel f, c’est-à-dire ! A=rf :
Terminologie : Une telle fonction fs’appelle une primitive de !(ou un potentiel de ! A).
Important : Dans ce cas, R!=f(B)f(A), où Aet Bsont les extrémités de l’arc .
En particulier, pour tout chemin fermé inclus dans U, on a H!= 0:On a en fait la caractérisation suivante :
Prop : Une forme di¤érentielle !est exacte ssi pour tout chemin fermé inclus dans U, on a H!= 0 :
Preuve : On peut supposer Uconnexe (c’est-à-dire que deux points de Usont reliés par un chemin continue).
Supposons H!= 0 pour tout chemin fermé. Alors la valeur de R!ne dépend que des bornes.
On …xe un point Odans U, et on dé…nit alors f(M)comme l’intégrale de !sur tout chemin reliant OàM.
On montre alors que fest de classe C1, et que df =!:

b) Formes di¤ érentielles fermées
Dé…nition : On dit qu’une forme di¤érentielle !: (x; y)7! a(x; y)dx +b(x; y)dy de classe C1est fermée ssi
@a
@y (x; y) = @b @x(x; y):
Remarque : Plus généralement, en dimension n,!:X7! Pn
i=1 ai(X)dxide classe C1est fermée ssi
8(i; j)2 f1;2; :::ng2,@ai
@xj
(X) = @aj
@xi
(X)
c) Théorème de Poincaré
Par le théorème de Schwarz, toute forme di¤érentielle de classe C1et exacte est fermée .
Théorème de Poincaré : Sur un ouvert étoilé, toute forme di¤érentielle de classe C1fermée est exacte .
Idée de la preuve : On considère un centre Ode l’ouvert étoilé. On dé…nit f(M) = R[OM]!, et on montre que !=df:
Exemple : La forme di¤érentielle != (x+y)dx + (xy)dy est exacte sur R2:
En e¤et, avec a(x; y) = x+yet b(x; y) = xy, on a @a
@y = 1 = @b @x , donc !est fermé, donc exacte (car R2est étoilé).
On cherche ftel que @f
@x =x+yet @f @y =xy, donc f(x; y) = 1 2x2+xy 1 2y2+kconvient, avec kconstante.
On peut aussi retrouver fpar la méthode générale, en considérant f(x; y) = R1
0
!
rf(tx; ty):(x; y)dt:
On obtient en e¤et f(x; y) = R1
0xa(tx; ty) + yb(tx; ty)dt =R1 0(x2+ 2xy y2)t2dt =1
2x2+xy 1 2y2:
Remarque : La propriété est fausse sur un ouvert quelconque. Par exemple, considérons sur U=R2n f(0;0)g,
!(x; y) = y
x2+y2dx +x x2+y2dy
Alors !est une forme di¤érentielle fermée, mais n’est pas exacte, car son intégrale curviligne sur le cercle unité
(paramétrée par t7! (cos t; sin t)) vaut 2, alors qu’elle serait nulle si la forme di¤érentielle était exacte.
3. Formule de Green-Riemann (dans R2)
a) Formule de Green-Riemann
Prop : Soit Kun compact de R2délimité par une courbe fermée de classe C1orientée dans le sens direct.
Soit !: (x; y)7! P(x; y)dx +Q(x; y)dy une forme di¤érentielle de classe C1dé…nie sur un ouvert Ucontenant K.
Alors HP(x; y)dx +Q(x; y)dy =RRK@Q
@x @P @y dxdy:
Remarque : On retrouve le fait que si !est une forme exacte, alors H!= 0:
Idée de la preuve : On prouve la propriété pour un rectangle, puis on approche Kpar des réunions de pavés (en
utilisant l’additivité des termes considérés).
b) Application à des calculs d’aires
On choisit Pet Qtels que @Q
@x @P @y =e
1. Ainsi, l’aire de Kdélimitée par (orienté dans le sens direct) vaut
Aire(K) = I x dy =I y dx
Exemple : Considérons K:x2
a2+y2 b21délimité par l’ellipse de paramétrage M() = (acos ; b sin ):
Alors Aire(K) = R2
0x()y0()d =ab R2 0(cos )2d =ab, car la valeur moyenne de (cos )2vaut 1
2: