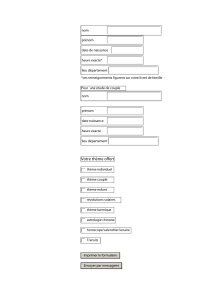
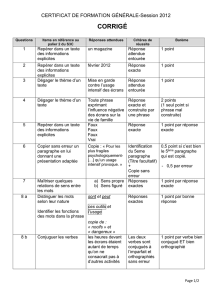
CNAM UE MVA 210 Ph. Durand Algèbre et analyse tensorielle

1
1
1URnU
L(Rn,R)Rnω
ω(x) = ω1(x)dx1+ω2(x)dx2+... +ωn(x)dxn
ωiCkωCk
1
Rn

R
fR
ω(x) = f(x)dx
UR
F
dF (x) = f(x)dx
ω
ω=dF
R
dω = 0 ddf = 0
R
R2
1
U U
U U

U
U
R
R R2
R
R
R2
ϕ U RnVRp
ω V
1ϕ∗ω
∀x∈U ϕ∗ω(x) = ω(ϕ(x))ϕ0(x).
URa b U
[a, b]ϕ[a, b]V
1

ϕ[a, b]URn
C1ω ϕ
Rb
aϕ∗ω=Rb aω(ϕ(t))ϕ0(t)dt.
Rn
ϕ t x(t)
ω(x) = ω1(x)dx1+ω2(x)dx2+... +ωn(x)dxn
x(t) = ϕ(t) = (x1(t), ...xn(t))
ω=ω1dx1+ω2dx2+... +ωndxn
1
ω=df
ω
ω=ω1dx1+ω2dx2+... +ωndxn∂f
∂x1dx1+∂f ∂x2dx2+... +∂f ∂xndxn
ω

∀(i, j)∈Nn
2∂ωi
∂xj
−∂ωj
∂xi= 0
dω = 0 rotω = 0
ω(x, y) = ω1(x, y)dx +ω2(x, y)dy
∂ω2
∂x −∂ω1 ∂y
ω
dω(x, y) = (∂ω2
∂x −∂ω1 ∂y )dx Vdy
1
1R
1C1
ω(x, y) = x
x2+y2dy −y x2+y2dx
UR2
ω