BREVET BLANC DE MATHEMATIQUES DU 25 JANVIER 2016.

BREVET BLANC DE MATHEMATIQUES DU 25 JANVIER 2016.
Exercice 1
Ce panneau routier indique une descente dont la pente est de 10%.
Cela signifie que pour un déplacement horizontal de 100 mètres, le dénivelé est de
10 mètres.
Le schéma ci-dessous n'est pas à l'échelle.
1) Déterminer la mesure de l'angle BCA que fait la route avec l'horizontale. Arrondir la réponse au degré.
2) Dans certains pays, il arrive parfois que la pente d'une
route ne soit pas donnée par un pourcentage, mais par
une indication telle que « 1 : 5 », ce qui veut alors dire
que pour un déplacement horizontal de 5 mètres, le
dénivelé est de 1 mètre.
Lequel des deux panneaux ci-contre indique la pente
la plus forte ?
Exercice 2
Cet exercice est un questionnaire à choix multiples (QCM). Pour chaque question, une seule des trois réponses
proposées est exacte. Sur la copie, indiquer le numéro de la question et écrire la réponse choisie en la justifiant.
Question
Réponse A
Réponse B
Réponse C
1
Combien vaut: 4
5 + 1 5  2 3 ?
14
15
2
3
6
20
2
25  (3)2 est égal à
75
45
15
3
Combien font 5% de 650 ?
32,5
645
13 000
4
Quelle est approximativement la masse de la Terre ?
32 tonnes
6  1024 kg
7  10–15 g
Exercice 1
4 points
Exercice 2
5 points
Exercice 3
5 points
Exercice 4
4 points
Exercice 5
6 points
Exercice 6
6 points
Exercice 7
3 points
Exercice 8
3 points
Présentation et rédaction, maîtrise de la langue
4 points
Dénivelé:
10 m
Route
Déplacement horizontal: 100 m
A
B C
Panneau A
Panneau B

Exercice 3
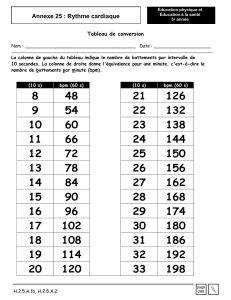
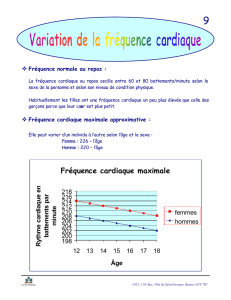
Lors d'une activité sportive, il est recommandé de surveiller son rythme cardiaque. Les médecins calculaient
autrefois la fréquence cardiaque maximale recommandée fm , exprimée en battements par minute, en soustrayant
de 220 l'âge a de la personne exprimé en années.
1) Traduire cette dernière phrase en utilisant une expression mathématique.
2) Des recherches récentes ont montré que cette expression devait être légèrement modifiée.
En notant fr la fréquence maximale recommandée, la nouvelle expression utilisée par les médecins est donnée
par: fr = 208 – (0,75 a).
a) Calculer fr pour a = 60 ans.
b) Déterminer l'âge pour lequel fr est égal à 184 battements par minute.
c) Sarah qui a vingt ans court régulièrement. Au cours de ses entraînements, elle surveille son rythme
cardiaque. Elle a ainsi déterminé sa fréquence cardiaque maximale recommandée et a obtenu
193 battements par minute.
Quand elle aura quarante ans, sa fréquence cardiaque maximale sera de 178 battements par minute.
Est-il vrai que sur cette durée de vingt ans, sa fréquence cardiaque maximale aura diminué d'environ 8% ?
Exercice 4
On donne le programme de calcul suivant:
 Choisir un nombre.
 Ajouter 1.
 Calculer le carré du résultat obtenu.
 Soustraire le carré du nombre de départ.
 Soustraire 1.
1) a) Effectuer ce programme lorsque le nombre choisi est 10 et montrer qu'on obtient 20.
b) Effectuer ce programme lorsque le nombre choisi est –3 et montrer qu'on obtient –6.
c) Effectuer ce programme lorsque le nombre choisi est 1,5.
2) Quelle conjecture peut-on faire à propos du résultat fourni par ce programme de calcul ? Démontrer cette
conjecture.
(Dans cette question, toute trace de recherche, même incomplète, ou d'initiative, même non fructueuse, sera prise
en compte dans l'évaluation.)
Exercice 5
1) a) Construire un triangle ABC isocèle en A tel que AB = 5 cm et BC = 2 cm.
b) Placer le point M de [AB] tel que BM = 2 cm.
c) Tracer la parallèle à [BC] passant par M. Elle coupe [AC] en N.
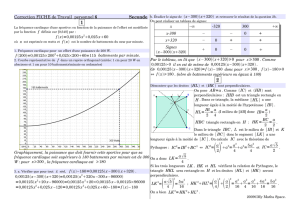
2) Calculer les longueurs MN et AN en justifiant.
3) Montrer que les périmètres du triangle AMN et du quadrilatère BMNC sont égaux.
Exercice 6
On considère le quadrilatère ABCD ci-contre et l'une de ses
diagonales [BD]. On donne les informations suivantes:
 L'angle BAD est droit
 BC = 8 cm
 CD = 6 cm
 DA = 2,8 cm
 BD = 10 cm.
(Attention, la figure n'est pas à l'échelle.)
1) Calculer la longueur AB.
2) Démontrer que BCD est rectangle.
3) Calculer l'aire du quadrilatère ABCD.
A B
C
D

Exercice 7
L'unité monétaire utilisée dans cet exercice est le franc polynésien (FP).
Une usine polynésienne fabrique du jus de fruits.
Soit C une fonction qui, à une quantité de jus de fruits fabriquée (en litres) associe le coût de fabrication (en
francs polynésiens).
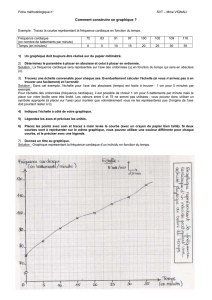
On a représenté sur le graphique ci-dessous la fonction C pour une quantité de jus comprise entre 0 et 130 litres.
À l'aide du graphique ci-dessus, répondre aux questions suivantes:
1) a) Donner le coût de fabrication de 100 litres de jus.
b) Pour quelles(s) quantité(s) de jus, le coût de fabrication est-il supérieur à 550 FP ?
2) a) Donner l'image de 85 par la fonction C.
b) Lire le(s) antécédent(s) de 600 par la fonction C.
Exercice 8
Un réservoir est constitué d'une pyramide régulière
à base carrée surmontée d'un parallélépipède rectangle:
AB = BC = 2 m ;
AE = 5 m ;
OI = 1,5 m ([OI] est la hauteur de la pyramide).
1) Calculer le volume du parallélépipède rectangle.
2) Calculer le volume de la pyramide.
3) En déduire le volume du réservoir lorsqu'il est plein.
B C
D
E
F G
H
I
O
A
10 20 30 40 50 60 70 80 90 100 110 120 130
100
200
300
400
500
600
700
Coût de fabrication en
francs polynésiens
Quantité de jus
en litres