Correction - My MATHS SPACE

Correction FICHE de Travail personnel 6 Seconde
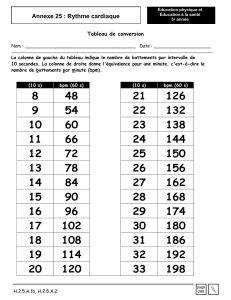
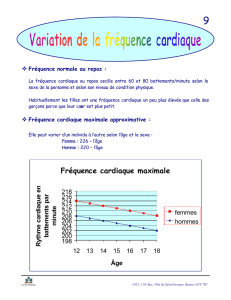
La fréquence cardiaque d'une sportive: en fonction de la puissance de l'effort est modélisée
par la fonction
f
définie sur [0;340] par :
fx=0,00125x20,025 x60
où
x
est exprimée en watts et
fx
est le nombre de battements du cœur par minute.
1. Fréquence cardiaque pour un effort d'une puissance de 200 W.
f200=0,00125×20020,025×20060=115
battements par minute.
2. Courbe représentative de
f
dans un repère orthogonal (unités: 1 cm pour 20 W en
abscisses et 1 cm pour 10 battements/minute en ordonnées)
Graphiquement, la puissance que doit fournir cette sportive pour que sa
fréquence cardiaque soit supérieure à 180 battements par minute est de 300
W : pour
x300
, la fréquence cardiaque est
180
3. a. Vérifier que pour tout
x
réel,
fx–180=0,00125x – 300x320
.
0,00125x–300x320=0,00125x2320x – 300 x – 96000
=0,00125x220 x–96000=0,00125x220×0,00125 x–0,00125×96000
=0,00125x20,025 x –120=0,00125x20,025 x60 –180=fx–180
b. Étudier le signe de
x–300x320
et retrouver le résultat de la question 2b.
On peut réaliser un tableau de signes:
x–∞ -320 300 +∞
x-300
–
–
0+
x+320
–
0+ +
Signes
x–300x320
+ 0
–
0
Par le tableau, on lit que
x – 300 x3200
pour
x300
. Comme
0,001250
il en est de même de
0,00125x – 300x320
.
Or
0,00125x–300x320=fx–180
donc pour
x300
,
fx–1800
⇔
fx180
. (nbre de battements supérieurs ou égaux à 180)
Démontrer que les droites
HL 
et
HK 
sont perpendiculaires.
On pose
AB=a
. Comme
IC
et
HB 
sont
perpendiculaires :
IHB
est un triangle rectangle en
H
. Dans ce triangle, la médiane
[HL ]
a une
longueur égale à la moitié de l'hypoténuse
[IB ]
.
HL=IB
2=a 4
.(I milieu de [AB] donc
IB=a
2
)
HBC
triangle rectangle en
H
:
HK =BC
2=a 2
.
Dans le triangle
IBC
,
L
est le milieu de
[IB ]
et
K
le milieu de
[BC ]
donc le segment
[LK ]
a une
longueur égale à la moitié de
[IC ]
. On calcule
IC
avec le théorème de
Pythagore :
IC2=IB2BC 2
⇔
IC2=
a
2
2
a2=a2
4a2=5a2 4
et
IC=a
5
2
.
On a donc
LK =a
5
4
.
Si les trois longueurs
LK
,
HK
et
HL
vérifient la relation de Pythagore, le
triangle
HKL
sera rectangle en
H
et les droites
HL 
et
HK 
seront
perpendiculaires.
LK 2=
a 5
4
2
=5a2
16
;
HK 2HL2=
a
4
2
a
2
2
=a2
16a2 4=a2 164a2 16 =5a2 16
.
On a bien
LK 2=HK 2HL2
.
2009©My Maths Space.
1
2