Vdouine – Troisième – Chapitre 3 – Thalès, Pythagore et trigonométrie

Vdouine – Troisième – Chapitre 3 – Thalès, Pythagore et trigonométrie
Acticités & exercices Page 1
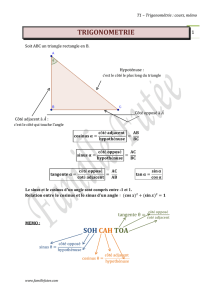
Enoncé du théorème
Etant données deux droites (BM) et (CN) sécantes en A.
Si les droites (BC) et (MN) sont parallèles alors
AM AN MN
AB AC BC
.
Application directe du théorème
Dans chacune des configurations suivantes :
 Deux droites sont sécantes,
 Deux droites sont parallèles.
Ecrire dans chaque cas les égalités données par
le théorème de Thalès.
Travail algébrique intermédiaire
Dans chacune des égalités proposées ci-dessous, déterminer algébriquement la valeur de la lettre.
5 20
3a
2
5 15
b
21
2 14
c
28 7
4d
10 2
15 e
16
24 6
f

Vdouine – Troisième – Chapitre 3 – Thalès, Pythagore et trigonométrie
Acticités & exercices Page 2
Configuration, rapports de longueurs et longueur manquante
On a proposé ci-dessous quatre configurations de Thalès, quatre formules et quatre résultats.
Associer à chacune des quatre situations proposées la formule et le résultat qui lui correspondent.
Situation 1
Situation 2
Situation 3
Situation 4
Formule a
Formule b
Formule c
Formule d
12 3
12 8
x
83
12 x
3
8 12
x
3
8 12
x
Réponse a
Réponse b
Réponse c
Réponse d
4,5x
2x
7,5x
6x
Agrandissement et réduction
Dans la situation 1, les points D,L, U sont alignés, les points D, V, N sont alignés et les droites
(LV) et (NU) sont parallèles. Dans la situation 2, les points T, M, F sont alignés, les points T, R,
B sont alignés et les droites (MR) et (FB) sont parallèles.
Situation 1
Situation 2
1. Dans la situation 1, quelle est la nature de la transformation permettant de passer du
triangle DLV au triangle DUN ? Précisez le rapport de cette transformation.
2. Dans la situation 2, quelle est la nature de la transformation permettant de passer du
triangle TFB au triangle TMR ? Précisez le rapport de cette transformation.
3. Dans chacune des deux situations déterminer la valeur de
x
.

Vdouine – Troisième – Chapitre 3 – Thalès, Pythagore et trigonométrie
Acticités & exercices Page 3
Longueurs manquantes dans une configuration de Thalès
Dans les quatre configurations suivantes, on a tracé deux droites sécantes et deux parallèles. Les
mesures sont données en centimètres et les figures proposées ne sont pas forcément à l’échelle.
Le but est de calculer, par un raisonnement précis que vous détaillerez, les nombres
x
et
y
.
1,6OE 
2,4OG 
2OB 
2,4BE 
OF x
FG y
1,5AL 
2AK 
2,4AI 
2,2KI 
LH x
AH y
Situation 1
Situation 2
3AB 
2,1AD 
6EB 
2,8AC 
EA x
DC y
Situation 3
5QR 
2,5MP 
2,5OR 
2PO 
OQ x
OM y
Situation 4
Dans les deux configurations suivantes, on a tracé sur la droite (AB) des segments de même
longueur. La droite (AC) coupe la droite (AB) en A et les droits (MN) et (BC) sont parallèles.
Le but est de calculer, par un raisonnement précis que vous détaillerez, les longueurs AM et MN.
Situation 5
Situation 6

Vdouine – Troisième – Chapitre 3 – Thalès, Pythagore et trigonométrie
Acticités & exercices Page 4
Situation 1
Thalès tient dans la main un bâton de
80 centimètres et fait face à une
pyramide.
Un jour de plein soleil, il place son
bâton verticalement, de telle sorte que
l’ombre portée par la pyramide et celle
portée par le bâton coïncident.
Ses assistants mesurent alors que l’ombre portée du bâton est de 1,20 mètres tandis que l’ombre
portée de la pyramide est de 15 mètres. Modéliser la situation décrite par une figure géométrique
puis, déterminer la hauteur de la pyramide.
Situation 2
Du haut de ses 1,50 mètre, Thalès observe le fond
d’un puit en se tenant à 1 mètre du bord comme
l’indique le schéma ci-dessous. Le puit mesure 1,20
mètre de diamètre. Modéliser la situation décrite
par une figure géométrique puis, déterminer la
profondeur du puits.
Situation 3
Une personne se tient à 60 centimètres du
bord d’un puits. Le puit est vide et a pour
diamètre 1,20 mètre. Du haut de ses 1,50
mètre cette personne aperçoit le fond du
puits. Modéliser la situation décrite par
une figure géométrique puis, déterminer
la profondeur du puits.
Situation 4
Lors d’une éclipse de soleil, les centres des trois astres sont alignés de telle sorte que l’ombre
portée de la lune sur la terre crée une zone pour laquelle le soleil est entièrement caché. Les
astronomes savent que le rayon du soleil mesure 696000 km et que celui de la lune mesure 1740
km. D’autre part, ils savent que la distance séparant le centre de la terre et le centre de la lune est
de 375000 km. Dans cet exercice la modélisation de la situation est déjà fournie (voir dessin ci-
dessous). Déterminer la distance séparant le centre de la terre et le centre du soleil.
Situation réelle
Modélisation

Vdouine – Troisième – Chapitre 3 – Thalès, Pythagore et trigonométrie
Acticités & exercices Page 5
Enoncé de la réciproque du théorème de Thalès
Si les points A, B, M et les points A, C, N sont alignés dans le même ordre et si
AM AN
AB AC
,
Alors les droites (BC) et (MN) sont parallèles.
Configuration classique
Configuration croisée ou papillon
Application de la réciproque du théorème
Démontrer que les droites (BD) et (CE) sont
parallèles. La réponse sera justifiée par un
raisonnement précis et détaillé.
Démontrer que les droites (CD) et (EF) sont
parallèles. La réponse sera justifiée par un
raisonnement précis et détaillé.
Dans les trois
configurations,
déterminer par un
raisonnement
précis et détaillé
si les droites
citées sont
parallèles.
Configuration 1 :
les droites (BE) et
(CD).
Configuration 2 :
les droites (GH)
et (IJ).
Configuration 3 :
les droites (LN)
et (KP).