Exercices régimes sinusoïdaux Sauf indication contraire, les

Exercices régimes sinusoïdaux
Sauf indication contraire, les tensions et intensités étudiées dans les exercices sont sinusoïdales.
Exercice 1
On considère deux tensions dont les valeurs instantanées sont données par les équations :
v1t=230 2sin.t1
et
v2t=200sin.t2
avec j1 = -60° et j2 = 45°
1. Donner la valeur de la phase à l'origine de v1(t) et la valeur efficace de v2(t).
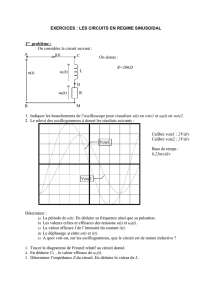
2. Les tensions v1(t) et v2(t) sont représentées sur le
graphe ci-contre, indiquer celle qui correspond à v1(t).
3. La tension v3(t) est égale à la somme de v1(t) et v2(t) :
v3(t) = v1(t) + v2(t)
a. Écrire les nombres complexes V1 et V2 associés à v1(t)
et v2(t) sous forme algébrique
b. En déduire la forme algébrique de V3 puis son module
et son argument.
c. Parmi les trois graphes ci-dessous, lequel correspond à v3(t) ?
Exercice 2
On considère deux tensions dont les valeurs instantanées sont données par :
v1t=230 2sin t
3
et
v2t=163sint−
6
1. Étude des nombres complexes associés
a. Écrire les nombres complexes V1 et V2 associés à v1(t) et v2(t) sous forme algébrique.
b. Placer leurs affixes dans le plan complexe (1 cm pour 40 V).
2. Addition de deux grandeurs sinusoïdales
a. Déterminer le nombre complexe V3 associé à la tension v3(t) telle que v3(t) = v1(t) + v2(t).
b. Calculer le module et l'argument de V3 (sans utiliser la détermination graphique).
c. Placer l’affixe de V3 dans le plan complexe.
d. Vérifier la concordance entre les calculs (question 2.b) et l’affixe de V3 dans le plan complexe (question
2.c).
Exercices régimes sinusoïdaux Page 1 TS1 ET 2011-2012

Exercice 3
1. Calculer l'impédance des dipôles suivants :
•Résistance de 10 Ω.
•Inductance de 40 mH à une fréquence de 50 Hz.
•Capacité de 220 µF à une fréquence de 100 Hz.
2. La tension aux bornes de chaque dipôle a une valeur efficace de 230 V. Calculer l'intensité efficace à
travers les dipôles et représenter les vecteurs de Fresnel associés à la tension et l'intensité.
Exercice 4
La valeur efficace de la tension aux bornes d'un dipôle est égale à 500 V et sa fréquence vaut 100 Hz.
L'intensité efficace du courant est de 10 A, il est en retard de 90° sur la tension.
Représenter les vecteurs associés à la tension et l'intensité sur un diagramme. Quelle est la nature du dipôle
(inductance, capacité ou résistance) ? Calculer son impédance et sa valeur (en H, en F ou en Ω).
Exercice 5
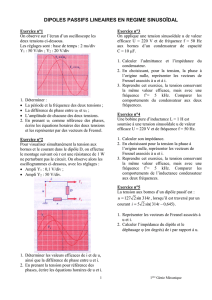
Le graphe ci-contre représente l'intensité et la tension pour
un dipôle qui peut être une inductance ou une capacité (le
dipôle est orienté avec la convention récepteur).
Échelle : 1 ms par division sur l' horizontale ; 100 V par
division pour la tension et 2 A par division pour l'intensité.
1. Représenter les vecteurs de Fresnel associés à la tension
et à l'intensité.
2. Préciser la nature du dipôle puis calculer son impédance.
3. Déterminer la période puis la fréquence de la tension.
4. Calculer l'inductance ou la capacité.
Exercice 6
Les graphes suivants représentent l'intensité et la tension pour un dipôle qui peut être une résistance, une
inductance ou une capacité. Représenter les vecteurs associés à la tension et à l'intensité, préciser la nature de
chaque dipôle puis calculer son impédance.
Échelles
horizontale : 0,5 ms par division
verticale : 100 V par division pour
la tension et 1 A par division pour
l'intensité.
Échelles
horizontale : 1 ms par division
verticale : 200 V par division pour
la tension et 5 A par division pour
l'intensité.
Échelles
horizontale : 1 ms par division
verticale : 100 V par division pour
la tension et 5 A par division pour
l'intensité.
Exercices régimes sinusoïdaux Page 2 TS1 ET 2011-2012

Exercice 7
1. La grandeur sinusoïdale représentée ci-dessous a
pour valeur efficace :
150 V -150 V 212 V Autre valeur à préciser :
...................
2. La tension représentée ci-dessous est
appliquée aux bornes d’un dipôle
d’impédance Z = 10 W. L’intensité qui le
traverse a pour intensité efficace :
10,0 A 7,1 A 4,1 A
Impossible à définir
Autre valeur à
préciser :
0
100
u(t) (V)
-100
t (ms)
10
3. Les oscillogrammes de u(t) et i(t) représentés ci-dessous peuvent correspondre à la tension et l’intensité
pour un condensateur orienté avec la convention récepteur :
Oui Non Impossible à définir
4. L'impédance d'une inductance augmente avec la fréquence : Vrai Faux Ça dépend
Exercice 8
Un dipôle est constitué d'une inductance L en série avec une résistance R. Lorsqu'une tension de valeur
efficace 230 V et de fréquence 50 Hz est placée aux bornes de ce dipôle, il est parcouru par un courant
d'intensité efficace égale à 12 A. Le courant est déphasé de 30° par rapport à la tension.
1. Représenter les vecteurs associés à la tension et à l'intensité.
2. Calculer le module et l'argument de l'impédance complexe du dipôle puis en déduire ses parties réelle et
imaginaire.
3. Représenter le dipôle et exprimer son impédance complexe en fonction de R, L et f.
Exercices régimes sinusoïdaux Page 3 TS1 ET 2011-2012

4. En identifiant les deux expressions obtenues, déterminer R et L.
Exercice 9
1. Le courant à travers une inductance est toujours en
retard sur la tension à ses bornes.
Vrai Faux Ça dépend
2. L'impédance d'un condensateur augmente avec la
fréquence.
Vrai Faux Ça dépend
3. Dans le montage représenté ci-dessous, l'intensité
i(t) est en retard de 90° sur la tension u(t).
Vrai
Faux
Ça dépend
4. Lorsque la fréquence augmente, l'intensité à
travers une capacité, dont la tension aux bornes a une
valeur efficace constante, diminue.
Vrai Faux Ça dépend
Exercice 10
Le graphe ci-contre représente la tension et l'intensité aux bornes
d'un dipôle.
1. Quelle est la nature du dipôle (capacitif, inductif ou résistif) ?
2. Mesurer le déphasage entre l'intensité et la tension puis
représenter les vecteurs associés sur un diagramme de
Fresnel.
3. Calculer l'impédance du dipôle.
Le modèle équivalent comporte une résistance R en série avec
une capacité C.
4. Représenter le schéma équivalent puis exprimer son
impédance complexe en fonction de R, C et f (fréquence des
signaux).
Échelles
- horizontale : 2,5 ms par division
- verticale : 100 V par division pour la
tension et 2 A par division pour
l'intensité.
5. Déterminer les parties réelle et imaginaire de l'impédance complexe à partir des résultats des questions 2
et 3. En déduire les valeurs de la résistance R et de la capacité C.
Exercice 11
1. Écrire l'impédance complexe du dipôle représenté ci-contre et
la mettre sous la forme
Z=RjL−1
C
(ω est la
pulsation de l'intensité à travers le dipôle). R = 10 Ω ; L = 21 mH et C = 53 µF
2. En déduire le module de Z (noté Z)en fonction de R, L, C et ω.
3. Calculer Z pour 50 Hz, 150 Hz et 250 Hz puis en déduire l'intensité efficace du courant à travers le dipôle
pour chacune de ces fréquences si la valeur efficace de u(t) est égale à 230 V.
4. Représenter les vecteurs de Fresnel associés à l'intensité, aux tensions aux bornes de la résistance, de
l'inductance et de la capacité pour chaque fréquence.
5. Mesurer le déphasage entre l'intensité et la tension aux bornes du dipôle pour chaque fréquence puis
préciser si le dipôle a un comportement inductif, capacitif ou résistif.
Exercices régimes sinusoïdaux Page 4 TS1 ET 2011-2012