``` uBAuAB =

UE103 – Optique géométrique - Devoir surveillé N°1 - 02/11/07 1/3
Université Pierre et Marie Curie - LP1 - UE 103 - Année 2004-2005
Optique géométrique - Devoir surveillé N°1
[email protected]
I) On considère une fibre optique (Figure 1) constituée par un cylindre centrale (le cœur)
d’indice n2 et d’une gaine cylindrique d’indice n1<n2. Montrer que tout rayon situé dans un
plan méridien de la fibre et faisant un angle θ avec l’axe reste prisonnier de la fibre si θ<β où
est β un angle que l’on exprimera en fonction de n1 et n2. Soit L la longueur de la fibre et c la
vitesse de la lumière dans le vide ; calculer la différence de temps mis par le rayon parcourant
le moins de temps dans la fibre et celui parcourant le plus de temps. A.N. : n2=1.6, n1=1, c=3
108 m/s et pour L prendre successivement L= 1m , 100 m et 10 km.
gaine
coeur
n2
n1
Figure 1
II) Soit une lentille mince convergente de centre O. Soit AB un objet et A’B’ son image à
travers la lentille (le point A est sur l’axe optique, voir Figure 2). On se place dans les
conditions de Gauss. Montrer que le grandissement transversal (Γ) de l’objet est tel que :
OA
OA
AB
BA ' '' =≡Γ .
Soit un rayon quelconque partant de A et convergeant en A’. On définit u l’angle que fait le
rayon incident avec l’axe optique et u’ l’angle que fait le rayon émergeant par rapport à l’axe
optique (voir Figure 2). Démontrer la relation :
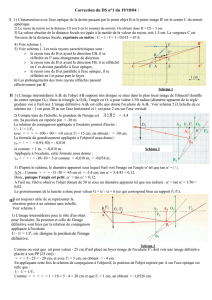
''' uBAuAB =appelée invariant de Lagrange-Helmholtz.
B
A
uA’
B’
u'
O
Figure 2
III) Soit une lentille mince convergente. Rechercher la distance minimale objet réel - image
réelle.

UE103 – Optique géométrique - Devoir surveillé N°1 - 02/11/07 2/3
Solutions :
I) La loi de Descartes appliquée à l’interface coeur-gaine s’écrit : n2 sin(π/2- θ) = n1 sin(r) où
r est l’angle que fait le rayon réfracté avec la normale à la surface. Il y’a donc réflexion totale
lorsque n1 sin(π/2- θ) > n2, i.e. lorsque cos(θ) > n1/n2.Définissons alors l’angle β tel que
cos(β)=n1/n2. Un faisceau est donc piégé dans la fibre lorsque θ<β.
Le temps de parcourt minimal est réalisé par le rayon passant par l’axe de la fibre. Celui-ci
met pour parcourir la distance L un temps L/v où v=c/n2 est la vitesse de parcourt de la
lumière dans le milieu n2. Le rayon qui effectue le trajet le plus long est celui dont l’angle θ
est le plus grand, i.e. à la limite l’angle θ=β . On voit aisément d’après la figure que ce rayon
parcourt, avant d’arriver à l’extrémité de la fibre, un nombre p de segments de longueurs
égales à la distance OM (voir figure). Le nombre P de segments est égal à p= L/ON. Or
cos(β)=ON/OM, donc la distance parcourue par ce rayon est p OM=L/cos(β) et le temps mis
par celui-ci est donc égal à Ln2/cos(β)/c. La différence de temps de parcourt entre le second et
le premier rayon est alors égal à Dt = L n2/c (n2/n1 – 1 ).
gaine
coeur
n2
n1
θ
θ
L
M
N
O
II) On voit aisément d’après la figure que tan (t)=A’B’/OA’= AB/OA d’où A’B’/AB=
OA’/OA. Considérons le faisceau lumineux A-I-A’. On a tan(u)= OI /AO et tan
(u’)=OI/A’O, il vient alors que tan(u) OA = tan(u’) OA’. Nous sommes dans les conditions
de Gauss par conséquent l’angle u est petit et par voie de conséquence l’angle u’ également.
On a donc u OA = u’ OA’. Multiplions cette équation par AB/OA. Il vient alors donc u AB =
u’ AB (OA’/OA) . Or d’après ce qui précède A’B’/AB= OA’/OA, d’où la relation de
Lagrange-Helmholtz : u AB = u’ AB.
B
A
uA’
B’
u'
O
I
t
t
III) Soit A’ l’image d’un objet A à travers la lentille de distance focale f’. La relation de
conjugaison s’écrit pour cet objet : '
11
'
1f
OAOA =− . Posons x=A’O et D= AA’. La relation de

UE103 – Optique géométrique - Devoir surveillé N°1 - 02/11/07 3/3
conjugaison s’écrit alors : '
111
fxxD =+ −. Différencions alors D et x, on a après quelques
calculs :
()
()
−
−
−= 2
2
211
x
xD
xD
dx
dD . La distance minimale est atteinte lorsque dD/dx=0.
Notons Dmin cette distance et xmin la position de A pour laquelle D est minimum. La distance
miniamle, Dmin, est donc tel que
(
)
2
min
2
minmin xxD =− , ce qui implique soit 0
min =D ou
minmin 2xD =. La première solution correspond à l’objet placé en O. Pour la seconde solution
utilisons la relation de conjugaison lorsque minmin 2xD =, il vient alors : '2
min fx =et ainsi
'4
min fD =.