OA n OF n 1

UE LP 103 – Optique géométrique – TD série n°2 – Corrigé - 30/11/09 1/4
Université Pierre et Marie Curie - LP1 - UE 103 - Année 2009-2010
[email protected]
TD Optique géométrique - Corrigés série n°2
1) Mesure de l’indice d’un liquide
La lentille plan convexe correspond à l’association d’un dioptre sphérique et d’un plan. On
considère une source à l’infini ie SA → ∞ et notons A’ son imagine à travers le dioptre
sphérique. La relation de conjugaison donne :
R
n
SA
n1
'
−
=
(1)
Notons maintenant F
1
’ l’image de A’ à travers le dioptre plan ; le dioptre plan correspond à un
dioptre sphérique de rayon de courbure infini, sa relation de conjugaison s’exprime donc :
0
1
''
1
=− OA
n
OF
(2)
La lentille étant mince, O et S sont considérés confondus (S=O). Les équations (1) et (2)
permettent de déduire la position de la focale du système : d
1
= OF
1
’ = R/ (n-1).
On ajoute maintenant le liquide d’indice n’ et on ajuste d de sorte que la face sortie coïncide
avec l’image de la source à l’infini, F
2
’ (nouveau point focal du système).
Ayant introduit le liquide, l’équation de conjugaison du dioptre plan se modifie comme :
0
''
2
'
=− OA
n
OF
n
(3)
Les équations (1) et (3) donnent ainsi :
1
'
'
22
−
==
n
nR
OFd
Il vient alors OF
2
’ / OF
1
’ = d
2
/ d
1
= n’.
2) Méthode de Bessel
La relation de conjugaison s’écrit pour une position O1 de la lentille : '
11
'
1
11
f
AOAO =− ,
relation qui peut s’écrire aussi :
'
1
'
'
11
f
AOAO
AA =
⋅
Posons D=AA’ et x=AO
1
. On établit alors la relation 0
'2
=+− fDDxx qui admet deux
solutions distinctes ssi 04
'2
>−=∆ fDD soit lorsque D>4 f ’.
Les deux solutions sont alors :
2
1
∆+
=D xet
2
2
∆−
=D x
3) Champ d’un miroir sphérique
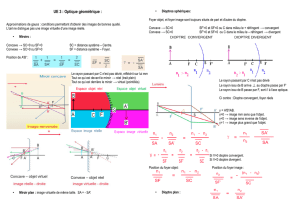
Pour construire M’, l’image de M considérons d’abord le rayon issu de M et passant par le
centre C. Ce rayon n’est pas dévié et est donc réfléchi par le miroir dans la direction CM.

UE LP 103 – Optique géométrique – TD série n°2 – Corrigé - 30/11/09 2/4
Puisque SP>>FS on peut considérer l’objet M à l’infini, par conséquent son image M’ est
nécessairement dans le plan foyer image du miroir. M’ est par conséquent à l’intersection du
rayon CM et du plan passant par F et orthogonal à l’axe optique (voir Figure 1). On a la
relation FM’/CF = PM/CP. Soit le rayon issu de M’ et allant au point d’observation O. Ce
rayon coupe le miroir au point U. La distance maximale PM observable est atteinte lorsque U
se situe à l’extrémité du miroir i.e. au point H . On a alors la relation SH/SO=FM’/OF. En
combinant les deux relations il vient l’expression pour PM : PM=SH (1+FS/SO) (2 + SP/FS).
L’ application numérique donne PM= 252 cm.
Figure 1
4) Télescope à deux miroirs sphériques
Soit A l’image à travers le premier miroir d’un point situé à l’infini. A est par conséquent
situé sur le plan focal du premier miroir. Soit A’ l’image de A à travers le second miroir. La
relation de conjugaison pour le couple de point conjugué (A,A’) s’écrit donc :
2
2222
221
'
1R
CSASAS ==+ . Soit A’B’ l’image de AB à travers le second miroir , le grandissement
de cette image vaut:
AS
AS
AB
BA
2
'
2
''' −=≡
γ
On veut d’une part |γ|= 3 et d’autre part que A’ soit confondus avec S1. Puisque S2S1 >0 et
S2F1 >0, on a γ<0. On veut donc 3
2
12
−=−= FS
SS
γ
, ce qui implique que S
2
S
1 = 3
S
2
F et donc
S
2
S
1=-3/2
S
1
F . Posons S
1
C
1=R1. Puisque
S
1
F
1=
S
1
C
1/2=R1/2. Il vient que donc
S
2
S
1=-3/4 R1.
Enfin, la relation de conjugaison permet d’établir que R2= S
2
S
1/2 soit R2=-3/8 R1.
5) Formule donnant la focale d’une lentille en fonction des
rayons de courbures
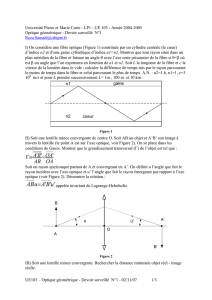
On considère un objet A placé à l’infini (ie S2A → ∞), notons A’ son image à travers le
premier dioptre et F’ l’image de A’ à travers le second dioptre.
La relation de conjugaison des dioptres sphériques donne, pour le premier dioptre :

UE LP 103 – Optique géométrique – TD série n°2 – Corrigé - 30/11/09 3/4
22
'
2
1
CS
n
AS
n
−
=
(1)
et pour le second :
11
'
1
'
1
11 CS n
AS
n
FS
−
=−
(2)
La lentille étant mince, O, S2 e t S1 sont confondus, soit O = S2 = S1. Les équations (1) et (2)
donnent alors l’expression pour la vergence :
−−=
−−=≡
12
1122
'
11
)1(
11
)1(
1RR
n
CSCS
n
OF
D
avec R2= C
2
S
2 et R1=
C
1
S
1.
6) Système de deux lentilles
a) Voir Figure 2.
b) Le trajet suivi par le rayon incident est le suivant :
O1
O2
Fc
F’c
F’d Fd
(1)
(2)
Fs
Figure 2
Le rayon incident étant parallèle à l’axe optique, il ressort de la lentille L1 (divergente)
dans une direction passant par le foyer image (F’d). Pour déterminer la direction du rayon
(1) à la sortie de la lentille L2 (convergente), on utilise un rayon (2) parallèle au rayon (1)
et passant par O2. Ces deux rayons correspondraient à un objet à l’infini ; ils convergent

UE LP 103 – Optique géométrique – TD série n°2 – Corrigé - 30/11/09 4/4
donc en un point, nommé foyer secondaire, situé sur le plan focal image de L2. Ce point
(Fs) est à l’intersection du rayon (2) avec le plan focal image de L2. Le rayon (1) étant
parallèle au rayon (2), il passe nécessairement par ce point.
c) Pour rendre le système afocal, il faut positionner Fc en F’d.
O1
Fc=F’d Fd F’c
Figure 3
7) Distance minimale objet-image
Soit A’ l’image d’un objet A à travers la lentille de distance focale f’. La relation de
conjugaison s’écrit pour cet objet :
'
11
'
1f
OAOA =−
. Posons x= A’O et D= AA’ . La relation de
conjugaison s’écrit alors :
'
111 fxxD =+
−
. Différencions alors D et x, on a après quelques
calculs :
( ) ( )
−
−
−=
2
2
2
11 x
xD
xD
dx
dD
. La distance minimale est atteinte lorsque dD/dx=0.
Notons Dmin cette distance et xmin la position de A pour laquelle D est minimum. La distance
miniamle, Dmin, est donc tel que
(
)
2
min
2
minmin xxD =−
, ce qui implique soit
0
min
=D
ou
minmin
2xD =
. La première solution correspond à l’objet placé en O. Pour la seconde solution
utilisons la relation de conjugaison lorsque
minmin
2xD =
, il vient alors :
'2
min
fx =
et ainsi
'4
min
fD =
.