TP 7 - DTU Compute

Vincent Neiger et Henri Lastakowski 2010–2011
Matlab – TP no7
Exercices de révision
1 Suite récurrente linéaire d’ordre 2
On considère la suite (un) définie par u1= 2,u2= 1 et pour n > 2, un=−5
6un−1+2 3un−2.
(En mathématiques, vous savez que ce problème admet une unique solution, et vous savez la
trouver !)
Q 1.a) Écrire une fonction qui calcule le n-ième terme de la suite.
Q 1.b) Tracer le graphe de (un)pour ncompris entre 1 et 100. Que peut-on conjec-
turer ?
Q 1.c) Tracer le graphe de (un)pour ncompris entre 1 et 300. La conjecture était-elle
correcte ? Que s’est-il passé ?
2 Calcul de racine carrée
De nombreuses fonctions (logarithme, exponentielle, cosinus...) ne se calculent pas directe-
ment, il faut prévoir un algorithme de calcul pour accéder (le plus rapidement possible) aux
résultats souhaités, généralement en n’utilisant que les quatres opérations de base (addition,
soustraction, multiplication et division).
Par exemple, pour le calcul de la racine carré d’un nombre A, un algorithme très efficace
est celui-ci :
– On part d’une valeur arbitraire u1>0.
– On calcule à chaque étape un+1 =1
2(un+A un).
– On s’arrête lorsque l’on a obtenu une précision suffisante.
Q 2.a) Se convaincre que la suite définie ainsi converge vers √A.
Q 2.b) Prendre A= 2, u0= 1, et écrire une fonction utilisant une boucle for pour
calculer le n-ième terme de la suite. Est-ce que la suite converge rapidement?
Q 2.c) À l’aide d’une boucle while, réécrire cette fonction pour s’arrêter lorsque l’on
a obtenu une précision de 10−k, k entier naturel.
Q 2.d) Connaissez-vous d’autres algorithmes pour calculer une racine carrée? (la
réponse est oui !). Si vous êtes en avance sur vos voisins, implémentez-les dans matlab et com-
parez l’efficacité des différents algorithmes.

Matlab – TP no7 Exercices de révision 2/2
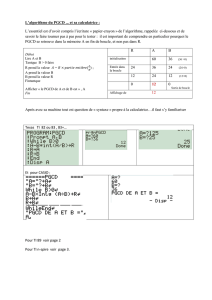
3 Division euclidienne et calcul du PGCD
Théorème (Division euclidienne).Pour tout entier naturel aet tout entier naturel non nul b, il
existe un unique couple d’entiers (q, r)tel que a=bq +ravec 06r < b.
Q 3.a) Écrire une fonction matlab qui retourne le quotient et le reste de la division
euclidienne de apar b. Pour cette question, il est interdit d’utiliser la fonction mod existant
dans matlab : vous n’avez le droit qu’à des soustractions, des comparaisons et l’utilisation de
boucles while.
L’algorithme d’Euclide pour trouver le pgcd de deux nombres aet best basé sur la remar-
que suivante :
On suppose que a≥b. Si b= 0, alors le pgcd de aet best a, sinon le pgcd de aet best égal
au pgcd de bet r, avec rle reste de la division euclidienne de apar b.
Par exemple pour a= 15 et b= 9, on aura successivement :
(a, b, r) = (15,9,6) →(9,6,3) →(6,3,0) →(3,0,−). Donc le pgcd est 3.
Q 3.b) Pour calculer des fonctions comme la factorielle, on connaissait le nombre
d’étapes à effectuer. Est-ce le cas ici ?
Q 3.c) Donner un algorithme qui calcule le pgcd de deux nombres, en utilisant une
boucle while.